【瞎口胡/史前巨坑】Treap 学习笔记

友情提示：这篇博文是写给自己复习的，可能写的比较烂，不建议初学者学习。

二叉搜索树（二叉排序树，BST）是一种特殊的二叉树。这种二叉树带点权（\(\text{key}\)），且它满足对于任意节点，其左子树中的节点的权值均小于它，右子树中的节点的权值均大于它。

容易发现，对任意一棵 BST 进行中序遍历，得到的序列递增。

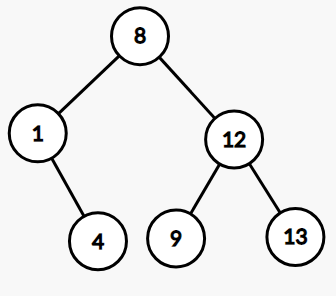
对上图中的 BST 进行中序遍历，得到 \([1,4,8,9,12,13]\)。

可以看看这道题。里面的操作 BST 都能做，也有很多博客讲过了。

容易发现，BST 的期望树高是 \(O(\log n)\) 的，然而，对于一个序列，其对应的 BST 不一定唯一。

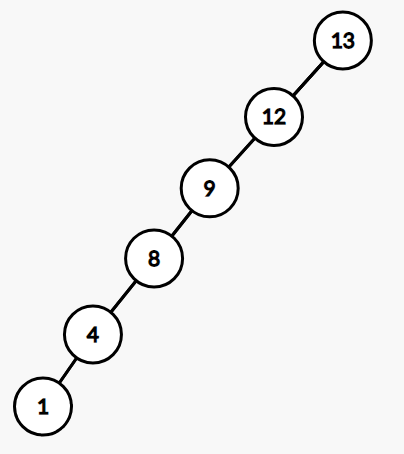
这棵 BST 的中序遍历和第一棵 BST 一样，但是树高增加了很多。对于这种 BST，树高变成了 \(O(n)\)，退化成了暴力，显然不够优秀。

所以我们需要一些措施来防止 BST 退化。最好写的就是 Treap 啦。

Treap 中，每个 BST 节点除了点权 \(\text{key}\) 还有随机权值 \(\text{rnd}\)。任意一棵 Treap 需要满足：

以节点的 \(\text{key}\) 为点权构成的二叉树符合 BST 的全部性质
以节点的 \(\text{rnd}\) 为点权构成的二叉树符合堆的全部性质

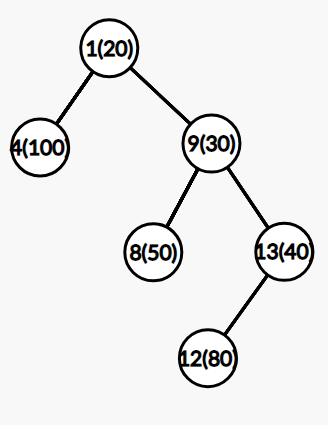
这棵树就是 Treap。但是因为 \(\text{rnd}\) 是随机的，最坏情况下仍然会退化。但是出题人总不会对着随机种子卡你啊，所以树高基本上是 \(O(\log n)\)。

推荐几个好用的随机种子：

\(114514\)，\(1919810\)，\(998244353\)，\(20071005\)
当然，srand(time(NULL)) 才是王道

那么这么优秀的平衡树要怎么写呢？

有两种 Treap，一种 Treap 带旋转，一种是非旋。带旋转的 Treap 难写难调，容易转错；非旋 Treap 好写，不容易出错。

非旋 Treap，又名 FHQ-Treap。核心操作是两个：split 和 merge。请忘掉上面所有的 BST 操作，基本用不着。

split

split 操作将一个 Treap 拆成 \(x,y\) 两棵，\(x\) 中所有 \(\text{key} \leq v\)，而 \(y\) 中所有 \(\text{key} > v\)。

void split(int now,int v,int &x,int &y){
	if(!now){ // 分完了
		x=y=0;
		return;
	}
	update(now); // 提前更新子树信息
	if(tree[now].val<=v){ // now 和 now 的左子树分到 x
		x=now;
		split(rc(now),v,rc(x),y); // 将 now 的右子树继续拆分
		update(x);
	}else{ // now 和 now 的右子树分到 y
		y=now;
		split(lc(now),v,x,lc(y));
		update(y);
	}
	return;
}

还有一种 split 以子树大小划分，中序遍历前 \(k\) 个分到 \(x\)，剩余部分分到 \(y\)。这种 split 在维护序列的时候非常有用（可以提取一个序列中的某个区间 \([l,r]\)）。

void split(int now,int k,int &x,int &y){
	if(!now){
		x=y=0;
		return;
	}
	update(now),pushdown(now); // 一部分序列维护问题需要区间打标记，在 split 前需要把所有标记下传
	if(tree[lc(now)].size<k){
		x=now;
		split(rc(now),k-tree[lc(now)].size-1,rc(x),y);
		update(x);
	}else{
		y=now;
		split(lc(now),k,x,lc(y));
		update(y);
	}
	return;
}

merge

merge 将两棵平衡树 \(x,y\) 合并成一棵。当 \(\max\limits_{a \in x} \{\text{key}_a \} \leq \max\limits_{b \in y} \{\text{key}_b \}\)（\(x\) 里面的任意 \(\text{key}\) 不比 \(y\) 中的大）的时候，这才是对的。

特殊地，在维护序列的时候，merge 操作的意义是将两个连续的区间合并成一个，但写法并没有改变。

void merge(int &now,int x,int y){
	if(!x||!y){
		now=x|y;
		return;
	}
	update(x),update(y);
	if(tree[x].rnd<tree[y].rnd){ // 维护堆性质（大根堆小根堆都行啦）
		now=x;
		merge(rc(now),rc(x),y);
		update(now);
	}else{
		now=y;
		merge(lc(now),x,lc(y));
		update(now);
	}
	return;
}

现在再来看看这道题。

插入 \(x\)

inline void Insert(int v){
	int x,a,b;
	NewNode(x,v); // 新建节点
	split(root,v,a,b); 
	merge(a,a,x);
	merge(root,a,b); // 记得合并回去
	return;
}

删除 \(x\)

因为有多个 \(x\) 时只删除一个，所以我们没办法直接将 \(\text{key}\) 等于 \(x\) 的子树提出来扔掉。将子树提出来之后，应该合并子树根的左右儿子成为一棵新子树，相当于消除了根节点。最后合并回去，就好啦。

inline void Delete(int v){
	int a,b,c;
	split(root,v,a,c);
	split(a,v-1,a,b);
	merge(b,lc(b),rc(b));
	merge(a,a,b);
	merge(root,a,c);
	return;
}

查询 \(x\) 的排名

将小于 \(x\) 的子树提出来，再加上 \(1\) 就是答案。

inline int Rank(int x){
	int a,b;
	split(root,x-1,a,b);
	int ans=tree[a].size+1;
	merge(root,a,b);
	return ans;
}

求第 \(x\) 大的数

BST 基本操作。

inline int Kth(int x,int k){
	assert(tree[x].size>=k); // 如果以 x 为根的子树大小 <= k，那一定传参数的时候写假了，抛出 RE 来检查
	while(1){
		if(k<=tree[lc(x)].size){
			x=lc(x);
		}else if(k==tree[lc(x)].size+1){
			return tree[x].val;
		}else{
			k-=tree[lc(x)].size+1;
			x=rc(x);
		}
	}
	return 114514; // 当然，这里是永远也跑不到的，但是控制流达到非 void 函数末尾会报错...
}

求 \(x\) 的前驱

将小于 \(x\) 的子树提出来，子树最大值就是答案。子树最大值可以 kth 求。

inline int GetPre(int x){
	int a,b;
	split(root,x-1,a,b);
	int ans=Kth(a,tree[a].size);
	merge(root,a,b);
	return ans;
}

求 \(x\) 的后继。

同上。

完整代码：

# include <bits/stdc++.h>
# define rr register
const int N=100010;
struct Node{
	int val,son[2],rnd,size;
}tree[N];
int root,cnt;
inline int &lc(int x){
	return tree[x].son[0];
}
inline int &rc(int x){
	return tree[x].son[1];
}
inline void NewNode(int &x,int v){
	x=++cnt;
	tree[x].rnd=rand(),tree[x].size=1,tree[x].val=v;
	return;
}
inline void update(int x){
	tree[x].size=tree[lc(x)].size+tree[rc(x)].size+1;
	return;
}
void split(int now,int v,int &x,int &y){
	if(!now){
		x=y=0;
		return;
	}
	update(now);
	if(tree[now].val<=v){
		x=now;
		split(rc(now),v,rc(x),y);
		update(x);
	}else{
		y=now;
		split(lc(now),v,x,lc(y));
		update(y);
	}
	return;
}
void merge(int &now,int x,int y){
	if(!x||!y){
		now=x|y;
		return;
	}
	update(x),update(y);
	if(tree[x].rnd<tree[y].rnd){
		now=x;
		merge(rc(now),rc(x),y);
		update(now);
	}else{
		now=y;
		merge(lc(now),x,lc(y));
		update(now);
	}
	return;
}
inline int Kth(int x,int k){
	assert(tree[x].size>=k);
	while(1){
		if(k<=tree[lc(x)].size){
			x=lc(x);
		}else if(k==tree[lc(x)].size+1){
			return tree[x].val;
		}else{
			k-=tree[lc(x)].size+1;
			x=rc(x);
		}
	}
	return 114514;
}
inline void Insert(int v){
	int x,a,b;
	NewNode(x,v);
	split(root,v,a,b);
	merge(a,a,x);
	merge(root,a,b);
	return;
}
inline void Delete(int v){
	int a,b,c;
	split(root,v,a,c);
	split(a,v-1,a,b);
	merge(b,lc(b),rc(b));
	merge(a,a,b);
	merge(root,a,c);
	return;
}
inline int Rank(int x){
	int a,b;
	split(root,x-1,a,b);
	int ans=tree[a].size+1;
	merge(root,a,b);
	return ans;
}
inline int GetPre(int x){
	int a,b;
	split(root,x-1,a,b);
	int ans=Kth(a,tree[a].size);
	merge(root,a,b);
	return ans;
}
inline int GetNext(int x){
	int a,b;
	split(root,x,a,b);
	int ans=Kth(b,1);
	merge(root,a,b);
	return ans;
}
inline int read(void){
	int res,f=1;
	char c;
	while((c=getchar())<'0'||c>'9')
		if(c=='-')f=-1;
	res=c-48;
	while((c=getchar())>='0'&&c<='9')
		res=res*10+c-48;
	return res*f;
}
void print(int x){
	if(!x)
		return;
	putchar('['),print(lc(x)),printf("%d(%d)",tree[x].val,tree[x].size),print(rc(x)),putchar(']');
	return;
}
int main(void){
	int n=read();
	while(n--){
		int opt=read();
		switch(opt){
			case 1:{
				Insert(read());
				break;
			}
			case 2:{
				Delete(read());
				break;
			}
			case 3:{
				printf("%d\n",Rank(read()));
				break;
			}
			case 4:{
				printf("%d\n",Kth(root,read()));
				break;
			}
			case 5:{
				printf("%d\n",GetPre(read()));
				break;
			}
			case 6:{
				printf("%d\n",GetNext(read()));
				break;
			}
			default:{
				break;
			}
		}
	}
	
	return 0;
}

posted @ 2020-08-28 10:23 Meatherm 阅读(211) 评论(0) 编辑收藏举报

刷新页面返回顶部

Loading

Meatherm 的奇妙博客

爱看看不看滚喵 (=•ェ•=)

【瞎口胡/史前巨坑】Treap 学习笔记

split

merge

公告