20201020 day40 洛谷十月月赛题解

第一次给月赛写题解，是因为个人觉得这四道题思维含量很高，顺便整理一下思路。

1 In the Dream

problem

一张\(n\)个点的完全图，求每条边只能经过一次的路径的长度最大值。

solution

一个图有欧拉回路的充要条件：图中只有0个或2个度数为奇数的点。
对于\(n\)为奇数，每个点的度都是\(n-1\)即为偶数，所以图中没有奇点，一定存在欧拉回路，每个点都可以和其他的点连接\(n-1\)个边，但是每两个点时间会重复一条边，答案是\(f(n)=\dfrac{n(n-1)}{2}(n=2k+1,k\in \mathbb N)\)

对于\(n\)为偶数，每个点的度都是\(n-1\)即为奇数，而我们只需要两个点是奇点，所以我们要使得\(n-2\)个点由奇数点改为偶数点，则每个点都需要删掉1条边，而每两个点会重复，一共删去了\(\dfrac{n-2}{2}\)，所以最终答案是

\[\begin{equation} f(x)=\left\{ \begin{array}{lr} \dfrac{x(x-1)}{2}(x=2k+1,k\in \mathbb N)& \\ \dfrac{x(x-1)}{2}-\dfrac{x-2}{2} (x=2k,k\in \mathbb N)& \end{array} \right. \end{equation}\]

thoughts

30pts：朴素dfs，时间复杂度\(O(n^{2^n})\)。

code

#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <iostream>
#include <queue>
using namespace std;
long long read(){
	long long a=0,op=1;char c=getchar();
	while(c>'9'||c<'0') {if(c=='-') op=-1;c=getchar();}
	while(c>='0'&&c<='9'){a*=10,a+=c^48,c=getchar();}
	return a*op;
}
long long T,n;
int main()
{
	T=read();
	while(T--){
		n=read();
		if(n%2!=0)
		printf("%lld\n",n*(n-1)/2);
		else printf("%lld\n",n*(n-1)/2+1-n/2);
	}
	return 0;
}

2 The fish and the Shield

problem

一个长为\(n+m\)的序列，每位上的数只可能是\(0,1,2\)，序列中有\(n\)个2，\(m\)个1。每次可以进行如下操作：

攻击：若该位上是2，则变成1，同时序列中所有的1变成2；若该位上是1，则变成0，没有其他变化。

询问将整个序列变成0的期望攻击次数。

subtask1:\(m=0\)
subtask2:\(n\le 10^{14},m\le 10^6\)

solution

考虑\(f(n,m)\)表示将\(n\)个2，\(m\)个1全部变成0的期望次数，我们首先考虑\(m=0\)。
\(f(n,0)\)进行一步操作变成\(f(n-1,1)\)，会有两种情况：

\[f(n-1,1)=\dfrac{1}{n}f(n-1,0)+\dfrac{n-1}{n}f(n-1,1)+1 \]

表示有\(\dfrac{1}{n}\)的概率打到1，有\(\dfrac{n-1}{n}\)的概率打到有2。
而我们知道概率为\(\dfrac{1}{p}\)的事件期望是\(p\)。
在递归过程中，\(f(n-1,1)\)无限递归，最终会被省略，每一步的操作次数是\(n+1\)，最终答案即为：

\[f(n-1,1)=\sum_{i=2}^{n+1}i \]

接下来考虑\(f(n,m)\)，类比上面的考虑：

\[f(n,m)=\dfrac{n}{m+n}f(n,m-1)+\dfrac{m}{m+1}f(n+m-1,1)+1 \]

其中\(f(n+m-1,1)\)使用上面的式子可以上面的结论\(O(1)\)计算，而后面的\(f(n,m-1)\)可以一直递推到\(f(n,1)\)也可以计算，最终我们可以得到\(f(n,m)\)的值。

实现上注意一些细节即可。

code

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e6+77,mod=998244353;
ll g[N],n,m;
struct M
{
	int n,m;
	ll _[4][4];
	M operator*(const M& o) const
	{
		M Res;
		Res.n=n,Res.m=o.m,memset(Res._,0,sizeof _);
		for(int i=0; i<n; i++) for(int k=0; k<m; k++) for(int j=0; j<o.m; j++) (Res._[i][j]+=_[i][k]*o._[k][j])%=mod;
		return Res;
	}
}F,A,B;
M power(M x,ll t)
{
	M b=x; t--;
	while(t)
	{
		if(t&1) b=b*x;
		x=x*x; t>>=1;
	}
	return b;
}
ll Power(ll x,ll t)
{
	if(x==0) return 0;
	x%=mod;
	ll b=1;
	while(t)
	{
		if(t&1) b=b*x%mod;
		x=x*x%mod; t>>=1;
	}
	return b;
}
int main()
{
	scanf("%lld%lld",&n,&m);
	F.n=1; F.m=3;
	F._[0][0]=0; F._[0][1]=1; F._[0][2]=1;
	A.n=3,A.m=3;
	A._[0][0]=1; A._[0][1]=0; A._[0][2]=0;
	A._[1][0]=1; A._[1][1]=1; A._[1][2]=0;
	A._[2][0]=1; A._[2][1]=1; A._[2][2]=1;
	B=A;
	if(n!=0) F=F*power(A,n);
	g[0]=F._[0][0];
	n%=mod;
	for(int i=1; i<=m; i++)
	{
		F=F*B;
		g[i]=(i*Power(n+i,mod-2)%mod*(g[i-1]+1)%mod+n*Power(n+i,mod-2)%mod*F._[0][0]%mod)%mod;
	}
	printf("%lld",g[m]);
}

3 The butterfly and Flowers

problem

给出一个长度为\(n\)的1,2序列，要求支持单点修改（修改之后仍然是1,2），查询一个区间和为\(k\)的区间，且使得左端点尽可能小。

thoughts

0pts：每次在原序列修改，询问时枚举左端点，对于每一个左端点开始向右扫描到一个和不小于\(k\)的位置，如果这一段区间和胃\(k\)即为答案。时间复杂度\(O(n^2m)\)
20pts：发现在左端点不断向右扫描的过程中，右端点的位置也一定单调不减。所以从上一次的右端点继续扫描即可。复杂度\(O(nm)\)。
20pts：做前缀和，设前缀和序列为\(s\)，问题转化为求最小的位置\(i,j\)使得\(s_j-s_i=k\)。
对于修改操作，相当于将序列\(s\)的一段后缀全部加上一个数，对于查询操作，可以枚举左端点，二份右端点，区间和为\(k\)即为答案。复杂度\(O(nm\log n)\)或者\(O(nm\log^2 n)\)。（没有上一个优秀吧...）
50pts：对于上一个解法，容易发现我们二分出的每一段区间和只能是\(k\)或\(k+1\)。如果和大于\(k+1\)的话，右端点向左移动一位和肯定不小于\(k\)，不满足我们二分的性质。

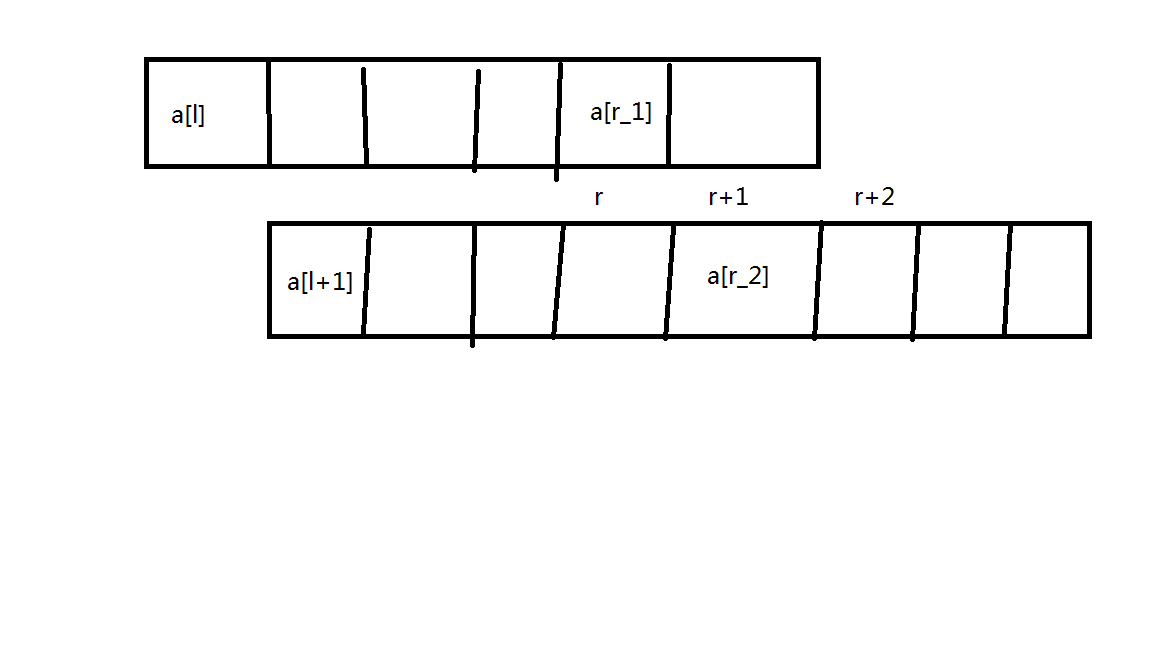
假设我们二分出来的两个区间是\([l,r_1],[l+1,r_2]\)，且两个区间的和都是\(k+1\)，那么：

\(a_l\)一定等于2，否则\([l+1,r_1]\)一定是一个合法的和为\(k\)的区间。
\(a_{r_1}\)一定等于2，否则\([l,r_1-1]\)一定是一个合法的和为\(k\)的区间。
\(r_2=r_1+1\)。因为如果\(r_2>r_1+1\)，那么其中\(a_l=a_{r_1}+a_{r_2}\)，又因为\(a_l=2,\therefore a_{r_1}+a_{r_2}=2\)，此时向左移动一个或两个都能得到一个区间和为\(k\)，所以不符合条件。

如果再加入一个区间\([l+2,r_3]\)，那么就有\(a_{l+1}=a_{r_2}=2,r_3=r_2+1\)。我们发现，只要接下来有一个位置不是2了，一定有一个和为\(k+1\)的区间，也就是答案区间与连续的2的个数有关。
我们用数据结构维护前缀和，对于每一次询问，二分出从位置1开始开始的和不小于\(k\)的区间\([1,p]\)。然后再用数据结构求出位置1和位置\(p\)后连续的2的个数，假设分别为\(cnt_1\)个和\(cnt_2\)个。

当\(cnt_1<cnt_2\)时，区间\([2+cnt_1,p+cnt_2]\)即为答案。
当\(cnt_1\ge cnt_2\)时，区间\([1+cnt_2,p+cnt_2]\)即为答案。
[手写小数据理解]

那么我们需要解决两个问题：

如何找到第一个前缀和不小于\(k\)的位置。
如何求出一个位置后面有多少个连续的2.

对于问题1，直接采用二分+数据结构即可。对于问题2，依然可以二分，假设长度为\(len\)，只需要判断区间\([p,p+len-1]\)的和是否是\(2len\)即可。
采用树状数组或者线段树实现均可。时间复杂度\(O(m\log^2n)\)

solution

100pts：在以上算法基础上，在数据结构里二分。树状数组二分或者线段树二分。时间复杂度\(O(m\log n)\)

code

#include <bits/stdc++.h>
using namespace std;
const int N=(2<<21)+10,LG=20,Inf=1e9;
int n,m,a[N];
char ch[3];
inline int read()
{
	int d=0; char ch=getchar();
	while (!isdigit(ch)) ch=getchar();
	while (isdigit(ch)) d=(d<<3)+(d<<1)+ch-48,ch=getchar();
	return d;
}
void write(int x)
{
	if (x>9) write(x/10);
	putchar(x%10+48);
}
inline void print(int x,int y)
{
	write(x); putchar(32);
	write(y); putchar(10);
}
struct BIT
{
	int c[N];
	inline void add(int x,int v)
	{
		for (int i=x;i<N;i+=i&-i)
			c[i]+=v;
	}
	inline int query(int x)
	{
		int ans=0;
		for (int i=x;i;i-=i&-i)
			ans+=c[i];
		return ans;
	}
	inline int query1(int k)
	{
		int p=0,sum=0;
		for (int i=LG;i>=0;i--)
		{
			int s=(1<<i);
			if (sum+c[p+s]<=k) p+=s,sum+=c[p];
		}
		return p;
	}
	inline int query2(int k)
	{
		int p=0,sum=0,pres=query(k-1);
		for (int i=LG;i>=0;i--)
		{
			int s=(1<<i);
			if (sum+c[p+s]-pres==(p+s-k+1)*2 || p+s<k)
				p+=s,sum+=c[p];
		}
		return p;
	}
}bit;
int main()
{
	n=read(); m=read();
	for (int i=1;i<=n;i++)
	{
		a[i]=read();
		bit.add(i,a[i]);
	}
	bit.add(n+1,Inf);
	while (m--)
	{
		scanf("%s",ch);
		if (ch[0]=='C')
		{
			int x=read(),y=read();
			bit.add(x,y-a[x]);
			a[x]=y;
		}
		else
		{
			int x=read(),pos=bit.query1(x);
			if (!x || x>bit.query(n)) puts("none");
			else if (bit.query(pos)==x) print(1,pos);
			else
			{
				pos++;
				int len1=bit.query2(1),len2=bit.query2(pos)-pos+1;
				if (len1<len2)
				{
					if (pos+len1<=n) print(2+len1,pos+len1);
						else puts("none");
				}
				else 
				{
					if (pos+len2<=n) print(1+len2,pos+len2);
						else puts("none");
				}
			}
		}
	}
	return 0;
}

4 Chess and Horses

problem

棋盘中有一个马，最开始在\((0,0)\)，它的每一步可以走一个\(a\times b\)的矩形，即为可以到达\((x\pm a,y\pm b)\)或者\((x\pm b,y\pm a)\)，其中\((x,y)\)表示当前马的坐标。
如果马可以通过上述移动方式到达棋盘上的任意一个点，那么\(p(a,b)=1\)，否则\(p(a,b)=0\)。
\(T\)组询问，每组询问会给出一个正整数\(n\)，求

\[\left( \sum_{a=1}^n\sum_{b=1}^np(a,b)\right)\operatorname{mod}2^{64} \]

thoughts

马能走到全图的充要条件是它能走到\((0,1)\)。考虑给出\(x,y\)求它能否走到\((0,1)\)。
5pts：暴力\(BFS\)或者打表。
20pts：下文中使用\((X,Y)\)表示当前马的坐标，\(x,y\)表示马一步走的矩形的长和宽。
考虑数论角度。
当\(\gcd (x,y)\neq 1\)时，显然不可以。因为走得顺序无所谓，所以可以把走的路程分成两段，一段只有\((X\pm x,Y\pm y)\)的位移，另一段是\((X\pm y,Y\pm x)\)的位移。（同时缩小最大公因数）
对于第一段能走到的点可以表示为\((2ax,2cy)\)或\((x+2ax,y+2cy)\)。第二段有\((2by,2dx),(2ax+x,2cy+y),a,b,c,d\in \mathbb Z\)，可得：

\[\begin{equation} \left\{ \begin{array}{lr} 2ax=2by& \\ 2cy=2dx+1& \end{array} \right. \end{equation}\]

\[\begin{equation} \left\{ \begin{array}{lr} 2ax+x=2by& \\ 2cy+y=2dx+1& \end{array} \right. \end{equation}\]

\[\begin{equation} \left\{ \begin{array}{lr} 2ax=2by+y& \\ 2cy=2dx+x+1& \end{array} \right. \end{equation}\]

\[\begin{equation} \left\{ \begin{array}{lr} 2ax+x=2by+y& \\ 2cy+y=2dx+x+1& \end{array} \right. \end{equation}\]

设\(k\)是任意整数。解第一个方程组得到\(2(ax-by)=0\)且\(2(cy-dx)=1\)，由于\(x,y\)互质，所以\((ax-by),(cy-dx)\)都可以表示成任意整数。所以就有\(2k=0\)或\(2k=1\)，显然无解。

同理第二个方程组可以推出\(2k+x=0,2k+y=1\)，即\(x\)为偶数，\(y\)为奇数。
第三个方程组推出\(2k-y=0,2k+y-x=1\)，即\(x\)为奇数，\(y\)为偶数。
第四个方程组推出\(2k+x-y=0,2k+y-x=1\)，显然无解。
所以\(p(x,y)=1\)当且仅当\(\gcd(x,y)=1\)且\(x+y\)为奇数。暴力求出\(p(x,y)\)即可。
50pts：如果\(x+y\)是一个奇数，那么\(x-y\)也是一个奇数，所以\(\gcd(x,x-y)=1\)且\(x-y\)是奇数也是\(p(x,y)=1\)的充要条件。
定义\(w(x)\)表示\([1,x]\)内有多少个奇数与\(x\)互质，考虑计算\(w(x)\)。
显然如果\(x\)是一个偶数，那么没有偶数与它互质，即\(w(x)=\phi (x)\)，我们不难发现\(ans=2\sum\limits_{i=1}^nw(x)-2\)
如果\(x\)是一个奇数，对于一个奇数\(k\)，有\(\gcd(x,k)=1\)，那么就有\(\gcd(x,x-k)=1\)，也就是说对于任何一个奇数都有一个对应的偶数\(x-k\)和它互质，也就是\(w(x)=\dfrac{\phi(x)}{2}\)，对于\(w(1)\)特判。
线性求\(\phi\)。

solution

100pts：显然答案就是奇数的\(\phi\)加上偶数的\(\phi\)除以2.
若\(n\)是一个偶数，假设我们已经求出了\(p_1=\sum\limits_{i=1}^{\dfrac{n}{2}}\phi(x)\)（\(x\)是奇数）和\(p_2=\sum\limits_{i=1}^{\dfrac{n}{2}}\phi(x)\)（\(x\)是偶数），那么考虑如何求到\(n\)。首先我们有\(\sum\limits_{i=1}^n\phi(x)[x=2k,k\in\mathbb N]=p_1+2p_2\)
解释：对于每一个奇数乘上2，根据\(\phi\)的定义我们发现它多了2这个因子。而\(n\)乘上了一个2，所以\(\phi\)不变；而对于偶数乘上了一个2，没有加减因子，但是\(n\)乘上了一个2，所以它的\(\phi\)也要乘2
使用杜教筛求出\(\sum\limits_{i=1}^n\phi(x)\)然后减去前面求出的答案就是奇数的答案。时间复杂度\(O(n\sqrt{n}\log n)\)，可以预处理\([1,10^7]\)以内的答案。

code

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<map>
#define ll unsigned long long
using namespace std;
const ll N=1e7+1;
ll T,n,cnt,mu[N],phi[N],pri[N];
ll sp1[N],sp2[N],p1[1100],p2[1100];
bool vis[N];
map<ll,ll> sp,sm; 
void prime(){
	phi[1]=1;
	for(ll i=2;i<N;i++){
		if(!vis[i])pri[++cnt]=i,phi[i]=i-1;
		for(ll j=1;j<=cnt&&pri[j]*i<N;j++){
			vis[pri[j]*i]=1;
			if(i%pri[j]==0){
				phi[i*pri[j]]=phi[i]*pri[j];
				break;
			}
			phi[i*pri[j]]=phi[pri[j]]*phi[i];
		}
	}
	for(ll i=1;i<N;i++){
		sp1[i]=sp1[i-1]+phi[i]*(i&1);
		sp2[i]=sp2[i-1]+phi[i]*(!(i&1));
	}
	return;
}
ll GetSphi(ll n){
	if(n<N)return sp1[n]+sp2[n];
	if(sp[n])return sp[n];
	ll rest=(n%2ull==0ull)?((ll)n/2ull*(n+1ull)):((ll)(n+1ull)/2ull*n);
	for(ll l=2ull,r;l<=n;l=r+1ull)
		r=n/(n/l),rest-=(r-l+1ull)*GetSphi(n/l);
	return (sp[n]=rest);
}
void dfs(ll x,ll n){
	p1[x]=p2[x]=0;
	if(n<N){
		p1[x]=sp1[n];
		p2[x]=sp2[n];
		return;
	}
	dfs(x+1,n/2);
	p2[x]+=p1[x+1]+p2[x+1]*2ull; 
	p1[x]+=GetSphi(n)-p2[x];
	return;
}
int main()
{
	prime();
	scanf("%llu",&T);
	while(T--){
		scanf("%llu",&n);dfs(0,n);
		printf("%llu\n",p1[0]+p2[0]*2ull-1ull);
	}
}

posted @ 2020-10-20 14:10 刘子闻阅读(147) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

刘子闻

试图掌握图论

20201020 day40 洛谷十月月赛题解

第一次给月赛写题解，是因为个人觉得这四道题思维含量很高，顺便整理一下思路。

1 In the Dream

problem

solution

thoughts

code

2 The fish and the Shield

problem

solution

code

3 The butterfly and Flowers

problem

thoughts

solution

code

4 Chess and Horses

problem

thoughts

solution

code

公告