20201005day27 模拟（七）

博弈论

博弈图和状态

如果将每个状态视为一个节点，再从每个状态向它的后继状态连边，我们就可以得到一个博弈状态图。

例如，如果节点 \((i, j, k)\) 表示局面为 \(i, j, k\) 时的状态，则我们可以画出下面的博弈图（由于篇幅有限，故仅显示部分状态节点和部分边）：

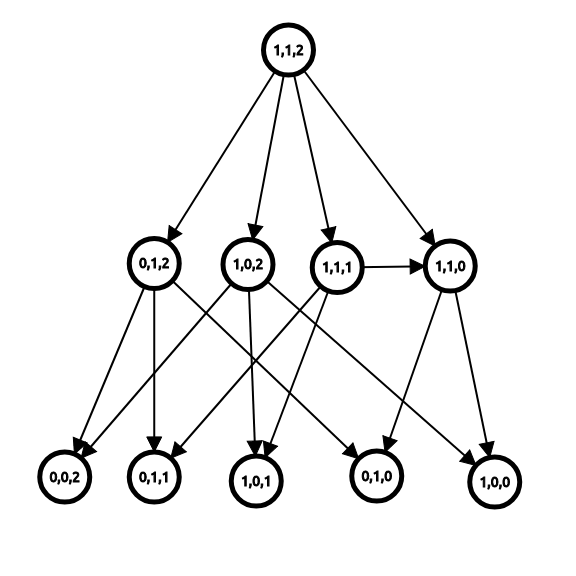
定义 必胜状态 为 先手必胜的状态 ， 必败状态 为 先手必败的状态 。

通过推理，我们可以得出下面三条定理：

• 定理 1：没有后继状态的状态是必败状态。
• 定理 2：一个状态是必胜状态当且仅当存在至少一个必败状态为它的后继状态。
• 定理 3：一个状态是必败状态当且仅当它的所有后继状态均为必胜状态。

对于定理 1，如果游戏进行不下去了，那么这个玩家就输掉了游戏。

对于定理 2，如果该状态至少有一个后继状态为必败状态，那么玩家可以通过操作到该必败状态；此时对手的状态为必败状态——对手必定是失败的，而相反地，自己就获得了胜利。

对于定理 3，如果不存在一个后继状态为必败状态，那么无论如何，玩家只能操作到必胜状态；此时对手的状态为必胜状态——对手必定是胜利的，自己就输掉了游戏。

如果博弈图是一个有向无环图，则通过这三个定理，我们可以在绘出博弈图的情况下用 \(O(N+M)\) 的时间（其中 \(N\) 为状态种数， \(M\) 为边数）得出每个状态是必胜状态还是必败状态。

Nim游戏

题面

\(n\)堆石子，第\(i\)堆有\(a_i\)，轮流取走一堆中的若干个，最终不能再取的获胜。

分析

结论：先手必胜，当且仅当\(a_1\oplus a_2\oplus ...\oplus a_n=0\).

蓝书证明

假设对于任意一个场面，有\(a_1\oplus a_2\oplus ...\oplus a_n=x\neq 0\)，则设\(x\)在二进制下最高位为1的那一位的位数为\(j\)，则这些堆石子中至少存在一堆石子\(a_k\)的二进制最高位为1的位数为\(j\)。可得\(a_p\oplus x<a_i(p\in \complement_{\{j\}}[1,n])\).我们就从\(a_i\)堆中取走若干石子，使其变为\(a_i\oplus x\)，得到了异或和为0的局面。
假设对于任意一个场面，有\(a_1\oplus a_2\oplus ...\oplus a_n=0\)，那么无论怎么取石子，都会使得异或和不为0.反证法：假设\(a_i\)变成\(a_i'\)，仍使得异或和为0.根据异或运算的消去律可得\(a_i=a_i'\)。与必须取的规则矛盾。

oi-wiki证明

为什么异或值会和状态的胜负有关？下面给出了这个定理的证明过程。

为了证明该定理，只需要证明下面三个定理：

• 定理 1：没有后继状态的状态是必败状态。
• 定理 2：对于 \(a_1 \oplus a_2 \oplus \ldots \oplus a_n \neq 0\) 的局面，一定存在某种移动使得 \(a_1 \oplus a_2 \oplus \ldots \oplus a_n = 0\) 。
• 定理 3：对于 \(a_1 \oplus a_2 \oplus \ldots \oplus a_n = 0\) 的局面，一定不存在某种移动使得 \(a_1 \oplus a_2 \oplus \ldots \oplus a_n = 0\) 。

对于定理 1，没有后继状态的状态只有一个，即全 \(0\) 局面。此时 \(a_1 \oplus a_2 \oplus \ldots \oplus a_n = 0\) 。

对于定理 2，不妨假设 \(a_1 \oplus a_2 \oplus \ldots a_n = k \neq 0\) 。如果我们要将 \(a_i\) 改为 \(a_i'\) ，则 \(a_i'=a_i \oplus k\) 。

根据异或定义，一定有奇数个 \(a_i\) 在 \(k\) 在二进制下的最高位为 \(1\) 。满足这个条件的 \(a_i\) 一定也满足 \(a_i > a_i \oplus k\) ，因而这也是个合法的移动。

对于定理 3，如果我们要将 \(a_i\) 改为 \(a_i'\) ，则根据异或运算律可以得出 \(a_i=a_i'\) ，因而这不是个合法的移动。

有向图游戏与\(\operatorname{SG}\)函数

题面

在一个有向无环图中，只有一个起点，上面有一个棋子，两个玩家轮流沿着有向边推动棋子，不能走的玩家为负。

分析

定义\(\operatorname{mex}\)函数的值为不属于集合\(S\)中的最小非负整数，即：

\[\operatorname{mex}(S)=\min{x}(x\notin S,x\in\mathbb N) \]

例如：\(\operatorname{mex}(\{0,2,4\})=1,\operatorname{mex}(\{1,2\})=0\).
对于状态\(x\)和它的所有\(k\)个状态\(y_1,y_2,...,y_k\)，定义\(\operatorname{SG}\)函数：

\[\operatorname{SG}(x)=\operatorname{mex}\{\operatorname{SG}(y_1),\operatorname{SG}(y_2),...,\operatorname{SG}(y_k) \} \]

而对于由\(n\)个有向图游戏组合的组合游戏，设他们的起点分别是\(s_1,s_2,...,s_n\)，则有定理：当且仅当\(\operatorname{SG}(s_1)\oplus\operatorname{SG}(s_2)\oplus...\oplus\operatorname{SG}(s_n)\neq 0\)时，这个游戏是先手必胜的。
这一定理被称为SG定理。

将Nim转换为有向图游戏

我们可以将一个有\(x\)个物品的堆视为节点\(x\)，当且仅当\(y<x\)时，节点\(x\)可以达到\(y\)。
那么，由\(n\)个堆组成的Nim游戏就可以视为\(n\)个有向图游戏了。
根据上面的推论，可以得出\(\operatorname{SG}(x)=x\)。再根据SG定理，就可以得出Nim和的结论了。

巴什博弈（Bash Game）

题面

只有一堆\(n\)个物品，两个人轮流从这堆物品中取物，规定每次至少取一个，最多取\(m\)个。最后取光者得胜。

分析

显然，如果\(n=m+1\)，那么由于一次最多只能取\(m\)个，所以，无论先取者拿走多少个，后取者都能够一次拿走剩余的物品，后者取胜。因此我们发现了如何取胜的法则：如果\(n=（m+1）r+s\)（\(r\)为任意自然数，\(s≤m\)),那么先取者要拿走\(s\)个物品，如果后取者拿走\(k(k≤m)\)个，那么先取者再拿走\(m+1-k\)个，结果剩下\((m+1)(r-1)\)个，以后保持这样的取法，那么先取者肯定获胜。总之，要保持给对手留下\((m+1)\)的倍数，就能最后获胜。

另一种分析

我们从最简单的情景开始分析
当石子有\(1\)~\(m\)个时，毫无疑问，先手必胜
当石子有\(m+1\)个时，先手无论拿几个，后手都可以拿干净，先手必败
当石子有\(m+2−2m\)时，先手可以拿走几个，剩下\(m+1\)个，先手必胜
我们不难发现，面临\(m+1\)个石子的人一定失败。
这样的话两个人的最优策略一定是通过拿走石子，使得对方拿石子时还有\(m+1\)个
我们考虑往一般情况推广
设当前的石子数为\(n=k(m+1)+r\)
先手会首先拿走\(r\)个，接下来假设后手拿走\(x\)个，先手会拿走\(m+1−x\)个，这样博弈下去后手最终一定失败
设当前的石子数为\(n=k(m+1)\)
假设先手拿\(x\)个，后手一定会拿\(m+1−x\)个，这样下去先手一定失败

变式

对于巴什博弈，那么我们规定，如果最后取光者输，那么又会如何呢？
\(n\mod(m+1)=0\)则后手胜利

1

solution

对于 x 的答案，我们将每个数都 \(\operatorname{mod}(x+1)\)，并求出异或和。假如异或和为0，则假如Alice 取某堆石子的数量超过了余数，Bob 可以取同一堆的石子使得余数变回去。如果Alice取的不超过某堆石子的余数，那么问题变为经典的 NIM 游戏，所以抑或和为 0 先手（Alice）必败，否则必胜。
所以问题变为求所有可能的 \(x\) 对应的\(a_i\operatorname{mod}(x+1)\)的异或和。

此处只有50分。

2

solution

一个显然的贪心是每次吃当前能吃的体积最大的鱼。
考虑直接模拟这个过程，可能会吃\(N\)次鱼。我们考虑当前不能吃的体积最小的鱼，显然只有我们的体积超过了这条鱼，我们的可选集合才会有变化，如果这条鱼的体积大于等于我们的目标，那我们只需要计算现有的集合需要吃几条能达到目标即可。
于是，我们每一步需要做的就是对于确定的数字集合，求出使得和达到某个值的最少步数即可，由于可选的数字是连续的，在线段树上二分即可。
接下来我们来分析数字范围变化的次数。考虑我们当前和为 \(A\)，不能选的最小体积是 \(B\)(显然 \(B>A\))，我们在选出一些数字之后，得到 \(A+x>B\)，接着我们得到了选不到的最小体积\(C\)，我们再次二分会得到\(A+x+y>C\)，注意到，\(y≥B\)，也就是说，\(A+x+y≥A+x+B>A+B>A+A\)，于是，我们在两次二分之后，手里的和至少翻倍，所以我们只需要 \(\log\) 次就一定能得到答案。

3

solution

结果的合法的分数的 \(x,y\) 的范围都只有 999，直接枚举两者，计算在询问范围内的倍数的数量即可。
时间复杂度\(O(V^2),V=999\)

4

solution

考虑 dp
表示前 \(i\) 位，集合 \(S\) 中的数字出现过，别的均没有出现过的方案数与十进制和。预处理出每种数字集合 \(S\) 后面可以跟哪些数字，然后直接转移即可。
由于答案很大，需要使用压位高精度。
时间复杂度 \(O(C2^kN)\)，其中 \(C\) 为高精度计算复杂度