20200911 day6 数论复习汇总
数论专题
编者:李昕烨、刘子闻、庄德楷
整理:刘子闻、李昕烨
资料来源:网络、集训课程
截稿:2020.9.11 于机房
1.公因数
求最大公因数
法1:更相减损术
//下面这个gcd函数在正int型内完全通用,返回a,b的最大公因数。
//但是当a,b之间差距较大时(如100000倍)会导致错误(栈过深)
int gcd(int a,int b){
if(a==b)return a;
else if(a>b)a-=b;
else b-=a;
return gcd(a,b);
}
int main(){
int a,b;
cin>>a>>b;
cout<<gcd(a,b)<<endl;
return 0;
}
法2:辗转相除法(欧几里得算法)
int gcd(int a,int b)
{
if(b==0) return a;
else return gcd(b,a%b);
}
直接在法1改进,效率倍增
int gcd(int x,int y){
return x%y==0?y:gcd(y,x%y);
}
法3:质因数分解
对\(a,b\)进行素因子分解:
注意:\(r_1,s_2\)等代表质因子需要乘的次数
则有
来自lzw的博客——质因数与质因数分解
质因数分解
void func(int x,vector<int>& r){
r.clear();
for(int i=2;i<=x;i++){
if(x%i==0){
while(x%i==0){
x/=i;
r.push_back(i);
}
}
}
}
//O(x)
void func(int x,vector<int>& r){
r.clear();
for(int i=2;i<=sqrt(x);i++){
if(x%i==0){
while(x%i==0){
x/=i;
r.push_back(i);
}
}
}
if(x!=1) r.push_back(x);
}
//O(sqrt(x))
void func(int x,vector<int>& r){
r.clear();
for(int i=2;i<=sqrt(x);i++){
if(x%i==0){
while(x%i==0){
x/=i;
r.push_back(i);
}
if(isprime(x)) break;
}
}
if(x!=1) r.push_back(x);
}
公因数
int gcd(int x,int y){
for(int i=min(a,b);i>=1;i--){
if(a%i==b%i){
...//最朴素的做法
}
}
}
int gcd(int x,int y){
if(y==0) return a;
if(x==0) return b;
if(a<=b) return gcd(b-a,a);
return gcd(a-b,b);
}//不停相减,这个挺慢的
int gcd(int x,int y){
return y==0?x:gcd(y,x%y)
}//从减改为模,快多了
int gg(int x,int y){
if(y==0) return a;
cnt+=a/b;
return gg(b,a%b);
}//计算需要相减多少次的算法
map的基本使用方法
map<int,int> mert;
int main(){
mert.clear();
mert[x]=y;
if(mert.count(x)){
//mert[x]!=0
}
map<int,int>::iterator it;
for(it=mert.begin();it!=mert.end();it++){
it->first;//x
it->second;//mert[x]
}
return 0;
}
int main(){
map<int/*prime*/,int/*cnt*/> mr;
}
求lcm
1 \(ab=\gcd (a,b) lcm (a,b)\)
2 使用map
2.拓展欧几里得算法(exgcd)
证明
用于求解形如\(ax+by=gcd(a,b)\)的不定方程特解。
当\(b=0\)时,可以看出\(gcd(a,b)=a\),而
此时
(实际上此时y大小不影响代码实现)
当\(b≠0\)时,递归求解\(exgcd(b,a\ mod\ b,x,y)\),设
可以求得\(a'x'+b'y'=gcd(a,b)\)的一组特解,即\(x'\),\(y'\)。
所以得到了递归结束后\(x\),\(y\)的表达式
证明如下:
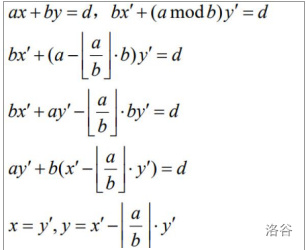
代码:
void exgcd(int a,int b,int &x,int &y)
{
if(!b)
{
x=1;
y=0;
return;
}
exgcd(b,a%b,x,y);
int p;
p=x;
x=y;
y=p-(a/b)*y;//x=y',y=x'-(a/b)*y'
return;
}
还有一种更短的
void exgcd(int a,int b,int &x,int &y)
{
if(!b)
{
x=1;y=0;
return;
}
exgcd(b,a%b,y,x)//x=y',y=x'
y-=(a/b)*x;//y=x'-(a/b)*y'
return;
}
根据递归,我们可以知道这个\((x, y)\)特解满足\(|x|+|y|\)最小
但是我们不满足求这一组解
如果设\(d = gcd(a,b)\)
那么:

所以x,y的解可以写成(\(x_0+kb',y_0-ka')\)
在此时,我们可以求出x,y最小非负整数解
分别是
xin=(x%b+b)%b;//最小非负整数解
yin=(y%a+a)%a;//最小非负整数解
xin=x>0&&x%b!=0?x%b:x%b+b;//最小正整数解
yin=y>0&&y%a!=0?y%a:y%a+a;//最小正整数解
//最大整数解可以通过代入求出
当然,我们看到上面的求证过程中一直没有出现用到
“\(ax+by\)右面是什么”
那么我们可以推广:
设a,b,c为任意整数,若方程\(ax+by=c\)其中一个解是\((x_0,y_0)\)
则它的任意整数解可以写成 \((x_0+kb',y_0-ka')\)
由此我们知道了任意整数解的求法,那\(ax+by=c\)的特解怎么求呢?

这里给出了一般性的做法,但为了编写代码方便
我们一般这么做
设
则
此时\(gcd(a',b')=1\),可以利用exgcd求出\(a'x'+b'y'=1\)的一组特解,继而得出
我们便求得了\(ax+by=c\)的一组特解。
代码
这里给出p5656的代码
//exgcd
#include <bits/stdc++.h>
#define int long long
using namespace std;
int gcd(int a,int b)
{
if(b==0) return a;
else return gcd(b,a%b);
}
void exgcd(int a,int b,int &x,int &y)
{
if(!b)
{
x=1;
y=0;
return;
}
exgcd(b,a%b,x,y);
int p;
p=x;
x=y;
y=p-(a/b)*y;//x=y',y=x'-(a/b)*y'
return;
}
signed main()
{
int t;
scanf("%lld",&t);
while(t--)
{
int a,b,c,x=0,y=0,xin,xax,yin,yax,npa=0,g;//分别是x,y最小,最大正整数解 ,和正整数解的数量
scanf("%lld%lld%lld",&a,&b,&c);
g=gcd(a,b);
if(c%g!=0) printf("-1\n");//裴蜀定理
else
{
a/=g;
b/=g;
c/=g;//eg:求6x+15y=15:a:6/3=2,b:15/3=5,c:15/3=5
//求2x'+5y'=1的一组解,x'=-2,y'=1
//则原解为x'*c,x=-10,y=5;
exgcd(a,b,x,y);//a'x+b'y=1
x*=c;
y*=c;
//xin=(x%b+b)%b;最小非负整数解
xin=x>0&&x%b!=0?x%b:x%b+b;
yax=(c-a*xin)/b;
//yin=(y%a+a)%a;最小非负整数解
yin=y>0&&y%a!=0?y%a:y%a+a;
xax=(c-b*yin)/a;
if(xax>0)//yax>0也行
npa=(xax-xin)/b+1;//正整数解数量
//npa=(yax-yin)/a+1;
if(npa==0)
{
printf("%lld %lld\n",xin,yin);
}
else printf("%lld %lld %lld %lld %lld\n",npa,xin,yin,xax,yax);
}
}
return 0;
}
来自lzw的博客——扩展欧几里得
//1
void exgcd(int a,int b,int &x,int &y){
if(!b){
x=1;y=0;return;
}
exgcd(b,a%b,x,y);
int temp;
temp=x;
x=y;
y=temp-(a/b)*y;
return ;
}
//2 紫书上的,更短更好背,也更容易让人迷糊
void exgcd2(int a,int b,int &x,int &y){
if(!b){
x=1;y=0;return ;
}
exgcd(b,a%b,y,x);
y-=(a/b)*x;
return ;
}
扩展欧几里得
定理:设\(a,b\)不全为0,则存在整数\(x,y\),使得\(\gcd (a,b)=ax+by\)
在不仅能求\(a,b\)的最大公约数\(r\),还要求出\(ax+by=r\)的一组\((x,y)\)整数解,那么我们就要用到拓展欧几里得算法。
使用迭代的方法,在辗转相除的过程中计算出\((x,y)\)。
用途:(A)求解不定方程(B)求解模的逆元(C)求解同余方程
找出一对整数\((x,y)\)使得\(ax+by=\gcd(a,b)\)
证明过程如下:
令\(ax+by=\gcd(a,b)=d\),有\(b'x+(a\mod b)y'=d\)
\[bx'+\left(a-\left\lfloor\dfrac{a}{b}\right\rfloor b \right)y'=d \]\[bx'+ay'-\left \lfloor \dfrac{a}{b} \right\rfloor by'=d \]\[ay'+b\left(x'-\left\lfloor \dfrac{a}{b} \right\rfloor y' \right)=d \]\[x=y',y=x'-\left\lfloor \dfrac{a}{b} \right \rfloor y' \]
变成了求\(bx'+(a\mod b)y'=d\)
然后再把这个式子递归下去,因为我们知道递归下去肯定会出现\(b=0\)的情况,此时我 们是可以求出\(x’\)和\(y’\)的,之后再不断代回去,就能够求出一组解了。
不能理解也没关系,代码会背就好了!
背代码!
//1
void exgcd(int a,int b,int &x,int &y){
if(!b){
x=1;y=0;return;
}
exgcd(b,a%b,x,y);
int temp;
temp=x;
x=y;
y=temp-(a/b)*y;
return ;
}
//2 紫书上的,更短更好背,也更容易让人迷糊
void exgcd2(int a,int b,int &x,int &y){
if(!b){
x=1;y=0;return ;
}
exgcd(b,a%b,y,x);
y-=(a/b)*x;
return ;
}
求出通解
为了求出更多的解,我们有:
前两个式子移项得到:
这个式子除以\(d\)得到:
显然\(a',b'\)互质,因此\(x_1-x_2=kb',y_2-y_1=ka',k\in Z\)
因此我们得到了:\(x_2=x_1-kb',y_2=y_1+ka',k\in Z\)
求出\(x\)作为最小正整数的解
用公式:\(x=(x\%b+b)\mod b\)
更一般的问题:裴蜀定理
更一般地,求解\(ax+by=c\)的问题
裴蜀定理:\(ax+by=c\)有解,当且仅当\(\gcd(a,b)|c\),即\(c=k\gcd(a,b),k\in Z\)
方程两边除以\(k\)得到:$$a\left( \dfrac{x}{k} \right)+b\left( \dfrac{y}{k} \right)=\gcd(a,b)$$
还元得到:\(ax_1+by_1=\gcd(a,b)\)
显然能够求出\(x_1,y_1\),因此也能求出原来的解
LGP1082 同余方程
求关于\(x\)的同余方程\(ax\equiv 1(\mod b)\)的最小正整数解。
题解
把这个同余式子转换一下就是\(ax\%b=1\),换句话说就是\(by+1=ax(y=\dfrac{a}{b})\)
移项之后得到\(ax+by=1\)(这样写的话\(y\)肯定就是负数了)
然后就用\(\operatorname{exgcd}\)即可。
有关伯特兰—切比雪夫定理
伯特兰—切比雪夫定理说明:若整数\(n > 3\),则至少存在一个质数\(p\),符合\(n < p < 2n − 2\)。
另一个稍弱说法是:对于所有大于\(1\)的整数\(n\),至少存在一个质数\(p\),符合\(n < p < 2n\)。
其中两个加强结果(定理):
定理 1: 对任意自然数\(n > 6\), 至少存在一个\(4k + 1\)型和一个\(4k + 3\)型素数 \(p\) 使得\(n < p < 2n\)。
定理 2: 对任意自然数\(k\), 存在自然数\(N\), 对任意自然数 \(n > N\)至少存在\(k\) 个素数\(p\)使得 \(n < p < 2n\)。
LGP5535 小道消息
有\(n\)个人,其中第\(i\)个人的衣服上有一个数\(i+1\),小X发现了一个规律:当一个衣服上的数为 \(i\) 的人在某一天知道了一条信息,他会在第二天把这条信息告诉衣服上的数为 \(j\)的人,其中$ \gcd(i,j)=1$(即 \(i,j\)的最大公约数为 \(1\))。在第 0 天,小 X 把一条小道消息告诉了第 \(k\) 个人,小 X想知道第几天时所有人都会知道这条小道消息。
可以证明,一定存在所有人都知道了这条小道消息的那一天。
提示:你可能需要用到的定理——伯特兰-切比雪夫定理。
\(2 \le n \le 10^{14}\)
\(1 \le k \le n\)
题解
- 答案只可能是1或2
- 当\(k+1\)是质数的时候
如果到\(n+1\)为止没有\(k+1\)的倍数时,显然答案为1
如果有倍数的话,答案就是2,感性理解很显然,证明也不难,\(2(k+1)\)一定与\(2(k+1)-1\) 互质 - 当\(k+1\)不是质数的时候
由那个奇怪的定理可知,一定存在一个质数\(p\)在\(\dfrac{n}{2}\)和\(n\)之间,显然\(k+1\)不可能是\(p\)的倍 数(\(2p>n\)),因此第一步先拿到p,然后 再由p传播到所有人
3.线性同余方程
对于形如 \(ax≡c(mod\ b)\) 的线性同余方程,
根据模运算的定义,在方程左侧添加一个\(by\)不会对结果造成影响,其实质就等价于\(ax+by=c\)的不定方程,利用exgcd求解便可。
注意:\(a≡c(mod\ b)\)有解的充要条件是:\(a-c\)是\(b\)的整数倍
例题
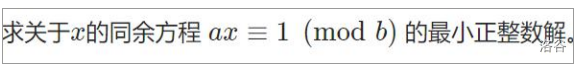
转换成\(ax\ mod\ b=1\)
转换成移项可得\(ax+by=1\)(保证y是负数)
之后用exgcd求解
代码:
//转化为求解ax+by=1
#include <bits/stdc++.h>
using namespace std;
void exgcd(int a,int b,int &x,int &y)
{
if(!b)
{
x=1;y=0;
return;
}
exgcd(b,a%b,x,y);
int temp=x;
x=y;
y=temp-(a/b)*y;
}
int main()
{
int a,b,x,y;
scanf("%d%d",&a,&b);
exgcd(a,b,x,y);
x=x>0&&x%b!=0?x%b:x%b+b;
printf("%d",x);
return 0;
}
拓展性质
$ax \equiv 1(mod\ b $称为同余方程的“逆”:a与b互质,且有唯一解
(注意:线性方程的唯一解是一组解)
它也是求解逆元的方法。。
4.乘法逆元
乘法逆元,一般用于求 \(\dfrac{a}{b} \pmod p\) 的值(\(p\)通常为质数),是解决模意义下分数数值的必要手段。
(1) exgcd
模数可以 不为质数
这个方法十分容易理解,而且对于单个查找效率似乎也还不错(尤其对于$ \bmod {p} $比较大的时候)。
这个就是利用拓欧求解 线性同余方程$ ax \equiv c \pmod {b}\(的\)c=1\(的情况。我们就可以转化为解\) ax + by = 1$这个方程。
求解这个方程的解。
而且这个做法还有个好处在于,当$ a \bot p$(互质),但 \(p\) 不是质数的时候也可以使用。
代码比较简单:
void Exgcd(ll a, ll b, ll &x, ll &y) {
if (!b) x = 1, y = 0;
else Exgcd(b, a % b, y, x), y -= a / b * x;
}
int main() {
ll x, y;
Exgcd (a, p, x, y);
x = (x % p + p) % p;
printf ("%d\n", x); //x是a在mod p下的逆元
}
(2)费马小定理
只适用于模数为质数的情况
若\(p\)为素数,\(a\)为正整数,且\(a\)、\(p\)互质。 则有\(a^{p-1} \equiv 1 (\bmod {p})\)。
另一个形式:
对于任意整数 $a $ ,有\(a^p \equiv \ a (mod \ p)\)
观察第一个公式:
这个我们就可以发现它这个式子右边刚好为 1 。
所以我们就可以放入原式,就可以得到:
\(a*x\equiv 1 \pmod p\)
\(a*x\equiv a^{p-1} \pmod p\)
$x \equiv a^{p-2} \pmod p $
所以我们可以用快速幂来算出 \(a^{p-2} \pmod p\)的值,这个数就是它的逆元了
ll fpm(ll x, ll power, ll mod) {
x %= mod;
ll ans = 1;
for (; power; power >>= 1, (x *= x) %= mod)
if(power & 1) (ans *= x) %= mod;
return ans;
}
(3) 线性算法
只适用于模数为质数的情况
用于求一连串数字对于一个\(\bmod p\)的逆元。
只能用这种方法,别的算法都比这些要求一串要慢。
首先我们有一个,\(1^{-1}\equiv 1 \pmod p\)
然后设$ p=k*i+r,(1<r<i<p)$也就是 $ k$ 是 $ p / i$ 的商, $r $ 是余数 。
再将这个式子放到\(\pmod p\)意义下就会得到:
然后乘上\(i^{-1},r^{-1}\)就可以得到:
$ i^{-1}\equiv -k*r^{-1} \pmod p $
\(i^{-1}\equiv -\lfloor \dfrac{p}{i} \rfloor*(p \bmod i)^{-1} \pmod p\)
于是,我们就可以从前面推出当前的逆元了。
注意:$ i ^{-1} * i ^{1} \equiv 1 $
#include <bits/stdc++.h>
#define ll long long
#define N 3000010
using namespace std;
ll inv[N];
int main()
{
int n,p;
scanf("%d%d",&n,&p);
inv[1]=1;
printf("1\n");
for(int i=2;i<=n;i++)
{
inv[i]=(ll)(p-p/i)*inv[p%i]%p;
printf("%lld\n",inv[i]);
}
return 0;
}
(4) 阶乘逆元法
只适用于模数为质数的情况
设$ f(i)=inv(i!)$, $ g(i)=i!\ $
则:$ f(i-1) = f(i) \times i $
证明
求证: $f(i-1)=\frac{1}{\ (i-1)\ !}=\frac{1}{i\ !}\times i =f(i)\times i $
假设要求 \([1,n]\) 中所有数的逆元
先求得 \([1,n]\) 中所有数的阶乘
再用费马小定理 求得\(f(n)\)的值
之后递推出 \(f(1 \sim n)\) 的值
但是 \(inv(1! \sim n! )\) 并不是我们想要的答案
需要继续转化。
可知 : $inv(i) = inv(i!) \times(i-1)\ ! $
-
证明 :
\(inv(i)=\frac{1}{i}=\frac{1}{i\ !}\times (i-1)\ ! = inv(i!)\times (i-1)!\)
按照上述方法转换,
可得:
$ inv(i)=f(i)\times (i-1)!$
即得答案 。
#include<cstdio>
#define ll long long
using namespace std;
ll mul(ll a,ll b,ll mod) //快速幂模板
{
ll ans=1;
while(b)
{
if(b&1) ans=ans*a%mod;
a=(a*a)%mod;
b>>=1;
}
return ans%mod;
}
ll n,p;
ll c[5000010]={1};
ll f[5000010];
int main()
{
scanf("%lld%lld",&n,&p);
for(int i=1;i<=n;i++)
c[i]=(c[i-1]*i)%p;
f[n]=mul(c[n],p-2,p); //获得inv(n!)
for(int i=n-1;i>=1;i--) //递推阶乘的逆元
f[i]=(f[i+1]*(i+1))%p;
for(int j=1;j<=n;j++) //转化并输出
printf("%lld\n",(f[j]*c[j-1])%p);
}
来自lzw的博客——有关逆元
探讨除法的取模。一种想法是将除法变成乘法,为此我们发明了逆元。
定义b的逆元:
\[inv_b=\left( \dfrac{1}{b} \right)\operatorname{mod }p \]
则 \(\dfrac{a}{b}\operatorname{mod }p=(a\times inv_b)\operatorname{mod }p\),那我们怎么求\(inv_b\)呢?
注意到\(\left( \dfrac{b}{b} \right)\operatorname{mod } p = (b\times inv_b)\operatorname{mod }p=1\)
换句话讲$$inv_b\times b\equiv 1(\operatorname{mod }p)$$
然后:把\(inv_b\)换成\(x\),\(b\)换成\(a\),\(p\)换成\(b\),然后:
就变成了LGP1082同余方程,解出的\(x\)就是\(a\)在\(\operatorname{mod }b\)意义下的逆元。
所以本质上是\(\operatorname{exgcd}\)求同余方程的解啦!
我懒啊我不想exgcd怎么办
当\(p\)为质数时,巧的是,费马小定理告诉我们\(b^{p-2}\times b\equiv 1(\mod m)\)
因此当\(p\)为质数的时候,\(inv_b=b^{p-2}\mod p\)
当然,注意费马小定理适用范围,如果超过这个适用范围就不存在逆元了。
这个要比\(\operatorname{exgcd}\)求解逆元更常见一些,但是限制条件更严格。
例题 LGP3811 【模板】乘法逆元
给定\(n,p\),求\(1\)~\(n\)中所有整数在模\(p\)意义下的乘法逆元。保证\(p\)为质数。\(n\le 3\times 10^6\)
费马欧拉都过不去。
我们需要一种线性求逆元的方式。
设\(p=ki+r,1<r<i<p\),也就是\(k\)是\(\dfrac{p}{i}\)的商,\(r\)的余数。
将这个式子放在模\(p\)意义下:\[ki+r\equiv 0(\operatorname{mod }p) \]然后乘上\(r^{-1}i^{-1}\)得到:
\[kr^{-1}+i^{-1}\equiv 0(\operatorname{mod }p) \]\[i^{-1}\equiv -kr^{-1}(\operatorname{mod }p) \]\[i^{-1}\equiv - \left \lfloor \dfrac{p}{i} \right \rfloor (p\mod i)^{-1}(\operatorname{mod } p) \]
代码:
inv[1]=1;
for(int i=1;i<=n;i++){
inv[i]=(p-p/i)*inv[p%i]%p;
}
逆元的应用
当你的答案是一个分数,而出题人不想用\(\operatorname{spj}\)的时候往往让你对分数取模。
所以逆元是作为一个工具存在的。
5.快速幂与大数乘积取模
快速幂
有二进制非递归和基本递归两种做法,代码呈现的是二进制非递归
#include <cstdio>
#include <cmath>
using namespace std;
int main(){
long long ans=1,i,j,k,m,n,b,p;
scanf("%lld%lld%lld",&b,&m,&p);
printf("%lld^%lld mod %lld=",b,m,p);
while(m>0){
if(m%2==1)
ans=ans*b%p;
b=b*b%p;
m=m>>1;
}
printf("%lld",ans%p);
return 0;
}
大数乘积取模
计算\((a\times b)\%p\)怎么办?\(((a%p)\times (b%p))\%p\)还是会溢出。
下面用到一种思想,神奇与上面的快速幂有异曲同工之妙,把\(b\)看成二进制表示。
举个栗子:\(4\times 13\%p\),看成是\(4\times 1101(2)\%p\),其实表示的是\(4\times (1\times 2^3+1\times 2^2+0\times 2^1+1\times 2^0)\%p\),那么我们在计算的时候就把b看成二进制,如果二进制最后一位是1,就说明这一位应该乘\(a\)取余,为零说明这一位不用乘\(a\),从低位开始不断将\(b\)的二进制式右移,同时将\(a\)乘以2,等同于把基数平方,原因见上式。
#include <iostream>
#define ll long long
using namespace std;
ll pow_mod(ll a,ll n,ll p)
{
a = a%p;
//首先降a的规模
ll res = 1;//记录结果
while(n)
{
if(n&1)
{
sum = (sum*a)%p;//n为奇数时单独拿出来乘
}
a = (a*a)%p;//合并a降n的规模
n >>= 1;
}
return res;
}//a^n mod p
ll mul_mod(ll a,ll b,ll mod)
{
ll res = 0;
while(b > 0)
{
if(b & 1) res = (res+a) % mod;
a = (a + a) % mod;
b>>=1;
}
return res;
}//a*b mod p
可以发现两者非常的相似,差别在于结果变量的初值和计算中加号和乘号的区别。
参考文章:
快速幂取模(详细),https://blog.csdn.net/dbc_121/article/details/77646508
大数乘法取模运算(二进制),https://www.cnblogs.com/geloutingyu/p/5886626.html
6.素数筛法
(1)Eratosthenes 筛法 (埃拉托斯特尼筛法)
时间复杂度是\(O(nloglogn)\) 。
int Eratosthenes(int n)
{
int p = 0;
for (int i = 0; i <= n; ++i) is_prime[i] = 1;
is_prime[0] = is_prime[1] = 0;
for (int i = 2; i <= n; ++i) {
if (is_prime[i]) {
prime[p++] = i; // prime[p]是i,后置自增运算代表当前素数数量
if ((long long)i * i <= n)
for (int j = i * i; j <= n; j += i)
// 因为从 2 到 i - 1 的倍数我们之前筛过了,这里直接从 i
// 的倍数开始,提高了运行速度
is_prime[j] = 0; // 是i的倍数的均不是素数
}
}
return p;
}
(2) Euler 筛法 (欧拉筛法)
时间复杂度\(O(n)\)。
代码中,外层枚举 \(i = 1 \to n\)。对于一个 \(i\) ,经过前面的腥风血雨,如果它还没有被筛掉,就加到质数数组 \(Prime[]\) 中。下一步,是用 \(i\) 来筛掉一波数。
内层从小到大枚举\(Prime[j]\)。 \(i×Prime[j]\) 是尝试筛掉的某个合数,其中,我们期望 \(Prime[j]\) 是这个合数的最小质因数 (这是线性复杂度的条件,下面叫做“筛条件”)。它是怎么得到保证的?
\(j\) 的循环中,有一句就做到了这一点:
if(i % Prime[j] == 0)
break;
-
下面用 \(s(smaller)\) 表示小于 \(j\)的数,\(L(larger)\) 表示大于 \(j\) 的数。
-
① \(i\) 的最小质因数肯定是 \(Prime[j]\)。
(如果 \(i\) 的最小质因数是 \(Prime[s]\) ,那么 \(Prime[s]\) 更早被枚举到(因为我们从小到大枚举质数),当时就要break)
既然 \(i\) 的最小质因数是 \(Prime[j]\),那么 \(i×Prime[j]\) 的最小质因数也是 \(Prime[j]\)。所以,\(j\) 本身是符合“筛条件”的。
- ② \(i×Prime[s]\) 的最小质因数确实是 \(Prime[s]\)。
(如果是它的最小质因数是更小的质数 \(Prime[t]\),那么当然 \(Prime[t]\) 更早被枚举到,当时就要break)
这说明 \(j\) 之前(用 \(i×Prime[s]\) 的方式去筛合数,使用的是最小质因数)都符合“筛条件”。
- ③ \(i×Prime[L]\) 的最小质因数一定是 \(Prime[j]\)。
(因为 \(i\) 的最小质因数是 \(Prime[j]\),所以 \(i×Prime[L]\) 也含有 \(Prime[j]\) 这个因数(这是 \(i\) 的功劳),所以其最小质因数也是 \(Prime[j]\)(新的质因数 \(Prime[L]\) 太大了))
这说明,如果 \(j\) 继续递增(将以 \(i×Prime[L]\) 的方式去筛合数,没有使用最小质因数),是不符合“筛条件”的。
#include <bits/stdc++.h>
using namespace std;
bool isprime[100000010];
int prime[6000010];
int cnt = 0;
void getprime(int n)
{
memset(isprime,1,sizeof(isprime));
isprime[1] = 0;//1不是素数
for(int i=2;i<=n;i++)
{
if(isprime[i]) prime[++cnt] = i;
for(int j=1;j<=cnt;j++)
{
if(i*prime[j]>n) break;
isprime[i*prime[j]] = 0;
if(i % prime [j] == 0) break;
}
}
}
int main()
{
int n,q;
scanf("%d%d",&n,&q);
getprime(n);
while(q--)
{
int k;
scanf("%d",&k);
printf("%d\n",prime[k]);
}
return 0;
}
来自lzw的博客——有关素数筛法
1.素数筛法
\(O(n)\)
#define maxn 1000010
bool prime[maxn];
int primes[maxn]
int num_prime=0;
void make_prime(){
prime[0]=prime[1]=false;
for(int i=2;i<=N;i++){
if(prime[i]){
primes[num_prime++]=i;
}
for(int j=0;j<num_prime &&i*primes[j]<N;j++){
prime[i*primes[j]]=false;
if(!(i%primes[j])){
break;
}
}
}
return ;
}
2.素数判断
bool check(int n){
int i;
for(int i=2;i*i<=n;i++){
if(n%i==0) return false;
}
return true;
}
3.质因数分解
考虑到若\(i\)满足\(n\% i=0\),则有\(n\% \dfrac{n}{i}=0\),所以可以仅枚举\(i\)从2到\(\sqrt{n}\)
时间复杂度\(O(\sqrt{n})\)
void decom(int n){
int i;
vector<int> res;
for(i=2;i*i<=n;i++){
while(n%i==0){
res.push_back(i);
n/=i;
}
}
for(i=0;i<res.size()-1;i++) printf("%d*",res[i]);
printf("%d\n",res.back());
}
如果事先已经用素数的线性筛法得到素数表了,那么有更快的方法进行质因数分解。
素数的线性筛法中国每一个合数n仅仅在i枚举到n除以n最小的素因子时被筛出,因此可以得到每一个合数最小的质因数。
对于要分解的合数n,先查表找到它最小的质因数,将其除掉,再找剩余的商种最小的质因数,依次操作,完成对n的分解。
这个过程仅仅需要\(O(\log n)\)
7.质数判断与复杂度的优化
根号算法
bool isprime(int x){
if(x==0||x==1) return 0;
if(x==2) return 1;
for(int i=3;i<=sqrt(x);i++){
if(x%i==0) return 0;
}
return 1;
}
单次时间复杂度:\(O(\sqrt{x})\)
判断1-n的素数个数:\(O(x\sqrt{x})\)
埃氏筛

时间复杂度:\(O(n\log(\log n))\)
埃氏筛的应用
1
题意描述
\(N\)组测试数据,求区间\([a,b]\)上的所有质数。
数据范围
\(N\leq 10^4,a,b\leq 10^6\)
#include<stdio.h>
#include<algorithm>
#include<math.h>
const int maxn=1e6+7;//总的范围规定在这里
using namespace std;
//我们将这个埃氏筛法写成一个函数
bool isprime[maxn];
void sieve(){
for(int i=0;i<=maxn;i++)isprime[i]=true;
isprime[0]=isprime[1]=false;
for(int i=2;i<=maxn;i++){//从2开始往后筛
if(isprime[i]){
for(int j=2*i;j<=maxn;j+=i){
isprime[j]=false;
}
}
}
}
int l,r;
int main(){
//我们在程序刚开始 先调用这个函数
//把这个isprime数组处理成我们想要的样子 用来判断素数
//这就是预处理的思想 我们在开头处理这一次
//把isprime数组 里面 下标是素数的全部变成了true
//后边想判断是不是素数 直接用isprime[i]是不是真就好了
sieve();
int cnt=0;//计数
scanf("%d%d",&l&r);//输入 l和r
for(int i=l;i<=r;i++){//遍历 l到r 判断就行了
if(isprime[i]){
cnt++;
}
}
printf("%d",cnt);
}
2
题意描述
输入一个数\(n\),判断他是不是素数,\(N\)组测试数据
数据范围
\(n\leq 10^6\)
题解
这个时候 就体现了 预处理的重要性
我们先预处理出来 1e6以内的所有素数 这样不管你输入啥 我直接去看 是不是素数就好了
预处理 按照一般的算法 20以内的素数需要60次才能判断出来
那1e6以内 大概需要1e9次(也就是十亿次)
而用埃氏筛法需要70万次
这就是这个算法的效率
#include<stdio.h>
#include<algorithm>
#include<math.h>
const int maxn=1e6+7;//总的范围规定在这里
using namespace std;
//我们将这个埃氏筛法写成一个函数
bool isprime[maxn];
void sieve(){
for(int i=0;i<=maxn;i++)isprime[i]=true;
isprime[0]=isprime[1]=false;
for(int i=2;i<=maxn;i++){//从2开始往后筛
if(isprime[i]){
for(int j=2*i;j<=maxn;j+=i){//这里可以优化,如下
isprime[j]=false;
}
}
}
}
int n;
int main(){
sieve();//预处理
//输入 n
while(scanf("%d",&n)!=EOF){
if(isprime[n]){
printf("Yes\n");
}
else{
printf("No\n");
}
}
}
这里有一个小优化,\(j\) 从 \(i \times i\) 而不是从 \(i + i\)开始,因为 \(i\times (2\)~$ i-1)$在 \(2\)~\(i-1\)时都已经被筛去,所以从\(i \times i\)开始。
埃氏筛法的缺陷:对于一个合数,有可能被筛多次。例如 \(30 = 2\times 15 = 3\times 10 = 5\times 6\)……那么如何确保每个合数只被筛选一次呢?我们只要用它的最小质因子来筛选即可,这便是欧拉筛法。
欧拉筛
欧拉筛法的基本思想 :在埃氏筛法的基础上,让每个合数只被它的最小质因子筛选一次,以达到不重复的目的。
int prime[maxn];
int visit[maxn];
void Prime(){
mem(visit,0);
mem(prime, 0);
for (int i = 2;i <= maxn; i++) {
cout<<" i = "<<i<<endl;
if (!visit[i]) {
prime[++prime[0]] = i; //纪录素数, 这个prime[0] 相当于 cnt,用来计数
}
for (int j = 1; j <=prime[0] && i*prime[j] <= maxn; j++) {
// cout<<" j = "<<j<<" prime["<<j<<"]"<<" = "<<prime[j]<<" i*prime[j] = "<<i*prime[j]<<endl;
visit[i*prime[j]] = 1;
if (i % prime[j] == 0) {
break;
}
}
}
}
对于visit[i*prime[j]] = 1 的解释
这里不是用i的倍数来消去合数,而是把 prime里面纪录的素数,升序来当做要消去合数的最小素因子。
打表观察来理解 :

发现i在消去合数中的作用是当做倍数的。
对于 i%prime[j] == 0 就break的解释
当 i是prime[j]的倍数时,i = kprime[j],如果继续运算 j+1,i * prime[j+1] = prime[j] * k prime[j+1],这里prime[j]是最小的素因子,当i = k * prime[j+1]时会重复,所以才跳出循环。
举个例子 :i = 8 ,j = 1,prime[j] = 2,如果不跳出循环,prime[j+1] = 3,8 * 3 = 2 * 4 * 3 = 2 * 12,在i = 12时会计算。因为欧拉筛法的原理便是通过最小素因子来消除。
附上欧拉筛代码:
/*求小于等于n的素数的个数*/
#include<stdio.h>
#include<string.h>
using namespace std;
int main()
{
int n, cnt = 0;
int prime[100001];//存素数
bool vis[100001];//保证不做素数的倍数
scanf("%d", &n);
memset(vis, false, sizeof(vis));//初始化
memset(prime, 0, sizeof(prime));
for(int i = 2; i <= n; i++)
{
if(!vis[i])//不是目前找到的素数的倍数
prime[cnt++] = i;//找到素数~
for(int j = 0; j<cnt && i*prime[j]<=n; j++)
{
vis[i*prime[j]] = true;//找到的素数的倍数不访问
if(i % prime[j] == 0) break;//关键!!!!
}
}
printf("%d\n", cnt);
return 0;
}
米勒罗宾素数检测
适用范围:较大数的较快素性判断
思路:
因为有好的文章讲解具体原理(见参考文章),这里只是把代码的大致思路点一下,读完了文章如果还有些迷糊,可以参考以下解释
原理是费马小定理(跳转):如果\(p\)是素数,则\(a^{p-1}%p==1\),加上二次探测定理:如果\(p\)是一个素数,\(x^2 \equiv 1(\mod p)\),则\(x=1\)或者\(x=n-1\)。
因为有通过费马小定理的伪素数的概率不是充分小,在此基础上加以改进判断。
一次检测中:
主要是把一个数\(n\)的\(n-1\)分解成\(d\times 2^r\)的形式,其中\(d\)为奇数,正向过程是\(a^n%p\)如果是1,就继续分解\(a^{\dfrac{n}{2}}%p\)(\(a\)为一个与\(n\)互素的数)看是否为1,;如果是\(n-1\)就停止分解,说明至此无法判断是否为素数;如果不等于这两个值,则一定为合数。而在写代码过程是这个过程的逆向过程,先分解到底,看最后这个\(a^d%p\)是否为\(1\)或\(n-1\),如果是说明已经分解到底了,也就是通过了此次素性测试。如果不是,说明在正向过程中出现了要么\(a\)的某次方为\(n-1\),根据算法停止了检测过程;要么就是中间的某一个结果不等于这两个数,那么就是合数。就从最后往前面推,每一步看满不满足上述条件。直到判断为合数或者终止检测的那一步。
多次检测过程:
不停更换\(a\)测试。
代码:(代码中可能需要用到快速幂和大数乘积取余,可以参考前面)
#include <iostream>
#include <time.h>
using namespace std;
long long an[] = {2,3,5,7,11,13,17,61};
long long Random(long long n)//生成0到n之间的整数
{
return (double) rand()/RAND_MAX*n+0.5;//(doubel)rand()/RAND_MAX生成0-1之间的浮点数
}
long long q_mod(long long a,long long n,long long p)
{
a = a%p;
//首先降a的规模
long long sum = 1;//记录结果
while(n)
{
if(n&1)
{
sum = (sum*a)%p;//n为奇数时单独拿出来乘
}
a = (a*a)%p;//合并a降n的规模
n /= 2;
}
return sum;
}
long long q_mul(long long a,long long b,long long p)
{
long long sum = 0;
while(b)
{
if(b&1)//如果b的二进制末尾是零
{
(sum += a)%=p;//a要加上取余
}
(a <<= 1)%=p;//不断把a乘2相当于提高位数
b >>= 1;//把b右移
}
return sum;
}
bool witness(long long a,long long n)
{
long long d = n-1;
long long r = 0;
while(d%2==0)
{
d/=2;
r++;
}//n-1分解成d*2^r,d为奇数
long long x = q_mod(a,d,n);
//cout << "d " << d << " r " << r << " x " << x << endl;
if(x==1||x==n-1)//最终的余数是1或n-1则可能是素数
{
return true;
}
while(r--)
{
x = q_mul(x,x,n);
if(x==n-1)//考虑开始在不断地往下余的过程
{
return true;//中间如果有一个余数是n-1说明中断了此过程,则可能是素数
}
}
return false;//否则如果中间没有中断但最后是余数又不是n-1和1说明一定不是素数
}
bool miller_rabin(long long n)
{
const int times = 50;//试验次数
if(n==2)
{
return true;
}
if(n<2||n%2==0)
{
return false;
}
for(int i = 0;i<times;i++)
{
long long a = Random(n-2)+1;//1到(n-1)
//cout << a << endl;
if(!witness(a,n))
{
return false;
}
}
return true;
}
int main()
{
long long num;
cin >> num;
if(miller_rabin(num))
{
cout << "Yes" << endl;
}
else
{
cout << "No" << endl;
}
}
时间复杂度:\(O(x^{\dfrac{1}{4}})\)
Matrix67,数论部分第一节:素数与素性测试,http://www.matrix67.com/blog/archives/234
c++的代码版本:
StanleyClinton,素数判定Miller_Rabin算法详解,https://blog.csdn.net/maxichu/article/details/45458569
素数密度
POJ2689:Prime Distance
给不超过int的\(l,r\),其中\(r-l+1 \le 10^6\),筛出其中的素数,并且求出相邻素数差值最大和最小的一对。
题解
- 提示:区间内的合数的质因子一定有在50000以内的
证明:如果不存在一个小于50000的,由于一个数至少有两个质因数,则大于50000的前两个质数\(m,n\)的乘积\(mn>50000^2>\text {int}\)
-
筛出50000以内的素数,用它们来筛出[l,r]内的合数.
怎么筛是个问题,假设我们有一素数\(p\)(并且筛完了素数\(p\)以前所有素数的倍数),我们显然希望找到第一个在区间内的素数的倍数,然后用筛法筛区间内的合数即可。 -
显然\(p^2\)是一个没被筛过的合数,如果\(p^2<L\),那么我们第一个筛的合数就应该是\((l+p- 1)/p*p\)(C++意义).
如果\(l\le p^2 \le r\),那么第一个筛的合数就是\(p^2\),如果\(p^2>r\)那就不用筛了。
然后对第一个筛的合数不断+p直到超过\(r\), 然后这些合数全筛走,剩下的就是质数. -
其余细节也有很多,很有必要一写。
8.扩展中国剩余定理(exCRT)
中国剩余定理(孙子定理)
强提醒:完全可以用excrt求解,且excrt适用范围更广,模数可以不互质
「物不知数」问题
有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二。问物几何?
即求满足以下条件的整数:除以 \(3\) 余 \(2\) ,除以 \(5\) 余 \(3\) ,除以 \(7\) 余 \(2\) 。
该问题最早见于《孙子算经》中,并有该问题的具体解法。宋朝数学家秦九韶于 1247 年《数书九章》卷一、二《大衍类》对「物不知数」问题做出了完整系统的解答。上面具体问题的解答口诀由明朝数学家程大位在《算法统宗》中给出:
三人同行七十希,五树梅花廿一支,七子团圆正半月,除百零五便得知。
\(2\times 70+3\times 21+2\times 15=233=2\times 105+23\) ,故答案为 \(23\) 。
算法简介及过程
中国剩余定理 (Chinese Remainder Theorem, CRT) 可求解如下形式的一元线性同余方程组(其中 \(n_1, n_2, \cdots, n_k\) 两两互质):
上面的「物不知数」问题就是一元线性同余方程组的一个实例。
算法流程
- 计算所有模数的积 \(n\) ;
- 对于第 \(i\) 个方程:
- 计算 \(m_i=\frac{n}{n_i}\) ;
- 计算 \(m_i\) 在模 \(n_i\) 意义下的 逆元 \(m_i^{-1}\) ;
- 计算 \(c_i=m_im_i^{-1}\) ( 不要对 \(n_i\) 取模 )。
- 方程组的唯一解为: \(a=\sum_{i=1}^k a_ic_i \pmod n\) 。
伪代码
n ← 1
ans ← 0
for i = 1 to k
n ← n * n[i]
for i = 1 to k
m ← n / n[i]
b ← inv(m, n[i]) // b * m mod n[i] = 1
ans ← (ans + a[i] * m * b) mod n
return ans
算法的证明
我们需要证明上面算法计算所得的 \(a\) 对于任意 \(i=1,2,\cdots,k\) 满足 \(a\equiv a_i \pmod {n_i}\) 。
当 \(i\neq j\) 时,有 \(m_j\equiv 0 \pmod {n_i}\) ,故 \(c_j\equiv m_j\equiv 0 \pmod {n_i}\) 。又有 \(c_i\equiv m_i(m_i^{-1}\bmod {n_i})\equiv 1 \pmod {n_i}\) ,所以我们有:
即对于任意 \(i=1,2,\cdots,k\) ,上面算法得到的 \(a\) 总是满足 \(a\equiv a_i \pmod{n_i}\) ,即证明了解同余方程组的算法的正确性。
因为我们没有对输入的 \(a_i\) 作特殊限制,所以任何一组输入 \(\{a_i\}\) 都对应一个解 \(a\) 。
另外,若 \(x\neq y\) ,则总存在 \(i\) 使得 \(x\) 和 \(y\) 在模 \(n_i\) 下不同余。
故系数列表 \(\{a_i\}\) 与解 \(a\) 之间是一一映射关系,方程组总是有唯一解。
例
下面演示 CRT 如何解「物不知数」问题。
- \(n=3\times 5\times 7=105\) ;
- 三人同行 七十 希: \(n_1=3, m_1=n/n_1=35, m_1^{-1}\equiv 2\pmod 3\) ,故 \(c_1=35\times 2=70\) ;
- 五树梅花 廿一 支: \(n_2=5, m_2=n/n_2=21, m_2^{-1}\equiv 1\pmod 5\) ,故 \(c_2=21\times 1=21\) ;
- 七子团圆正 半月 : \(n_3=7, m_3=n/n_3=15, m_3^{-1}\equiv 1\pmod 7\) ,故 \(c_3=15\times 1=15\) ;
- 所以方程组的唯一解为 \(a\equiv 2\times 70+3\times 21+2\times 15\equiv 233\equiv 23 \pmod {105}\) 。(除 百零五 便得知)
应用
某些计数问题或数论问题出于加长代码、增加难度、或者是一些其他不可告人的原因,给出的模数: 不是质数 !
但是对其质因数分解会发现它没有平方因子,也就是该模数是由一些不重复的质数相乘得到。
那么我们可以分别对这些模数进行计算,最后用 CRT 合并答案。
下面这道题就是一个不错的例子。
给出 \(G,n\) ( \(1 \leq G,n \leq 10^9\) ),求:
$$G^{\sum_{k\mid n}\binom{n}{k}} \bmod 999911659$$
首先,当 \(G=999~911~659\) 时,所求显然为 \(0\) 。
否则,根据 欧拉定理 ,可知所求为:
现在考虑如何计算:
因为 \(999~911~658\) 不是质数,无法保证 \(\forall x \in [1,999~911~657]\) , \(x\) 都有逆元存在,上面这个式子我们无法直接计算。
注意到 \(999~911~658=2 \times 3 \times 4679 \times 35617\) ,其中每个质因子的最高次数均为一,我们可以考虑分别求出 \(\sum_{k\mid n}\binom{n}{k}\) 在模 \(2\) , \(3\) , \(4679\) , \(35617\) 这几个质数下的结果,最后用中国剩余定理来合并答案。
也就是说,我们实际上要求下面一个线性方程组的解:
而计算一个组合数对较小的质数取模后的结果,可以利用 卢卡斯定理 。
比较两 CRT 下整数
考虑 CRT, 不妨假设 \(n_1\leq n_2 \leq ... \leq n_k\)
与 PMR(Primorial Mixed Radix) 表示
\(x=b_1+b_2n_1+b_3n_1n_2...+b_kn_1n_2...n_{k-1} ,b_i\in [0,n_i)\)
将数字转化到 PMR 下,逐位比较即可
转化方法考虑依次对 PMR 取模
其中 \(c_{i,j}\) 表示 \(n_i\) 对 \(n_j\) 的逆元, \(c_{i,j}n_i \equiv 1 \pmod {n_j}\)
扩展:模数不互质的情况
两个方程
设两个方程分别是 \(x\equiv a_1 \pmod {m_1}\) 、 \(x\equiv a_2 \pmod {m_2}\) ;
将它们转化为不定方程: \(x=m_1p+a_1=m_2q+a_2\) ,其中 \(p, q\) 是整数,则有 \(m_1p-m_2q=a_2-a_1\) 。
由裴蜀定理,当 \(a_2-a_1\) 不能被 \(\gcd(m_1,m_2)\) 整除时,无解;
其他情况下,可以通过扩展欧几里得算法解出来一组可行解 \((p, q)\) ;
则原来的两方程组成的模方程组的解为 \(x\equiv b\pmod M\) ,其中 \(b=m_1p+a_1\) , \(M=\text{lcm}(m_1, m_2)\) 。
多个方程
用上面的方法两两合并就可以了……
扩展中国剩余定理
给定\(n\)组非负整数\(a_i,b_i\),求解关于\(x\)的方程组的最小非负整数解。
让我们来改变一下格式:
把(1)(2)相减得:
用\(\operatorname{exgcd}\)求解,不能解就无解。
然后我们可以解出一个最小正整数解\(y_1\),带入(1)得到\(x\)其中一个解:
由于我们知道,\(y_1\)的全解,
那么x的全解是
由\(y_1\)的全解可导
即:\(x\equiv x_0(\ mod\ \operatorname{lcm}(a_1,a_2))\)
则:\(x+y_3\operatorname{lcm}(a_1,a_2)=x_0(4)\)
把(3)(4)再联立
即可求解
#include <bits/stdc++.h>
#define ll long long
using namespace std;
int n;
const int maxn = 1e5+7;
ll ai[maxn],bi[maxn];
ll exgcd(ll a,ll b,ll &x,ll &y)
{
if(!b)
{
x=1;
y=0;
return a;
}
ll gcd = exgcd(b,a%b,x,y);
ll p = x;
x = y;
y = p - (a/b)*y;
return gcd;
}
ll mul(ll a,ll b,ll mod)
{
ll res = 0;
while(b > 0)
{
if(b & 1) res = (res+a) % mod;
a = (a + a) % mod;
b>>=1;
}
return res;
}
ll excrt()
{
ll x,y,k;
ll M = ai[1],ans = bi[1];//第一个方程的解特判,分别是模数,等于数
for(int i=2;i<=n;i++)
{
ll a = M,b = ai[i],c = ((bi[i] - ans)%b +b)%b;//ax ≡c(mod b)
ll gcd = exgcd(a,b,x,y),bg = b / gcd;
if(c % gcd != 0) return -1;
x =mul(x , c / gcd , bg);
ans += x * M;//更新前k个方程组的答案
M *= bg;//M为前k个模数的lcm
ans = (ans % M + M) % M;
}
return (ans % M + M) % M;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%lld%lld",&ai[i],&bi[i]);//模数,乘数
}
printf("%lld",excrt());
return 0;
}
看过代码之后,我们再考虑具体的编程问题。
假设已经求出前\(k-1\)个方程组成的同余方程组的一个解为\(x\)
且有\(M=\prod_{i-1}^{k-1}m_i\)
(代码实现中用的就是\(M=LCM_{i-1}^{k-1}m_i\),显然易证这样是对的,还更能防止溢出)
则前\(k-1\)个方程的方程组通解为\(x+i*M(i\in Z)\)
那么对于加入第\(k\)个方程后的方程组
我们就是要求一个正整数t,使得 \(x+t*M \equiv a_k(\mod m_k)\)
转化一下上述式子得 \(t*M \equiv a_k-x(\mod m_k)\)
对于这个式子我们已经可以通过扩展欧几里得求解t
若该同余式无解,则整个方程组无解, 若有,则前k个同余式组成的方程组的一个解解为\(x_k=x+t*M\)
所以整个算法的思路就是求解k次扩展欧几里得
9.关于取模问题
仍要记得开\(\operatorname{long long}\)!!
取模铭记“能取就取”!
公式:
一定要记住乘法仍有可能爆\(\operatorname{int}\)
10.欧拉函数与欧拉定理
\(\phi (n)\)指不超过n并且与n互素的正整数的个数。
定理1:对于\(n=p_1^{a_1}p_2^{a_2}...p_n^{a_n}\),有\(\phi (n)=\phi (p_1^{a_1})\phi (p_2^{a_2})...\phi (p_n^{a_n})\)
定理2:\(p\)为素数,则\(\phi (p)=p-1\).该定理充要。
定理3:\(p\)为素数,\(a\)是正整数,则\(\phi (p^a)=p^a-p^{a-1}\)
定理4:\(m,n\)为互质,则\(\phi (mn)=\phi (m)\phi (n)\).
定理5:\(p\)为奇数,则\(\phi (2n)=\phi (n)\).
定理6:\(n\)为大于2正整数,则\(\phi (n)\)是偶数.
定理7:\(n\)为正整数,则\(\sum _{d\mid n} \phi(d)=n\).
欧拉定理
对于任何两个互质的正整数($\ a \bot m\ \() ,且\)a,m(m\geq 2)$
有\(a^{\phi(m)}\equiv 1(\mod m)\)
所以 \(a^b\equiv a^{b\bmod \varphi(m)}\pmod m\)
费马小定理
欧拉定理中\(m\) 为质数时,\(a^{m-1}\equiv 1(\mod m)\)【欧拉定理+定理2】
应用:利用欧拉函数求不超过n且与n互素的正整数的个数,其次可以利用欧拉定理与费马小定理来求得一个逆元,欧拉定理中的m适用任何正整数,而费马小定理只能要求m是质数。
拓展欧拉定理
扩展欧拉定理无需 \(a,m\) 互质。
当 \(a,m\in \mathbb{Z}\) 时有:
来自lzw的博客——欧拉函数
欧拉函数
欧拉函数\(\varphi (x)\)的值为在\([1,x)\)的区间内与x互质的数的个数
通式:\(\varphi (x)=x\prod\limits_{i=1}^{n}(1-\dfrac{1}{p_i})\)其中\(p_1,p_2,...,p_n\)为\(x\)的所有质因数,x是不为0的整数。\(\varphi (1)=1\)。
注意:每种质因数只一个。 比如\(12=2\times 2\times 3\)那么\(\varphi (12)=12 \times (1-\dfrac{1}{2}) \times (1-\dfrac{1}{3})=4\)
介绍几个性质:
- 若\(x\)是质数\(p\)的\(k\)次幂,则\(\varphi (x)=p^k-p^{k-1}=(p-1)p^{k-1}\),因为除了\(p\)的倍数外,其他数都跟\(x\)互质。
- 积性函数——若m,n互质,\(\varphi(mn)=\varphi(m)\varphi(n)\)。
- 当\(x\)为质数时,\(\varphi(2x)=\varphi(x)\),其实与上述类似。
- 若\(x\)为质数则\(\varphi(x)=x-1\), 这个挺重要的。
- 一个数的所有质因子之和\(S\)是\(S=\dfrac{n\varphi(n)}{2}\).
具体应用: - 若\(a,n\)互质,则\(a^{\varphi (n)} \equiv 1(\mod n)\)
- \(a^b=a^{b \mod \varphi(m)+\varphi (m)}\)
//用通式算的
int euler(int n){ //返回euler(n)
int res=n,a=n;
for(int i=2;i*i<=a;i++){
if(a%i==0){
res=res/i*(i-1);//先进行除法是为了防止中间数据的溢出
while(a%i==0) a/=i;
}
}
if(a>1) res=res/a*(a-1);
return res;
}
//筛选法打欧拉函数表
#define Max 1000001
int euler[Max];
void Init(){
euler[1]=1;
for(int i=2;i<Max;i++)
euler[i]=i;
for(int i=2;i<Max;i++)
if(euler[i]==i)
for(int j=i;j<Max;j+=i)
euler[j]=euler[j]/i*(i-1);//先进行除法是为了防止中间数据的溢出
}
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define N 100000
int primes[N], euler[N], cnt;
bool st[N];
/* 欧拉函数
可以在 O(n) 的时间复杂度内求出 1~n中所有数的欧拉函数 同时也能算质数
质数存在primes[]中(用cnt统计<=n的素数个数),euler[i] 表示 i的欧拉函数*/
int get_eulers(int n) {
euler[1] = 1;
for (int i = 2; i <= n; i ++ ) {
if (!st[i]) {
primes[cnt ++ ] = i;
euler[i] = i - 1;
}
for (int j = 0; j < cnt && i * primes[j] <= n; j ++ ) {
st[primes[j] * i] = true;
if (i % primes[j] == 0) {
euler[i * primes[j]] = euler[i] * primes[j];
break;
}
euler[i * primes[j]] = euler[i] * (primes[j] - 1);
}
}
return cnt;
}
int main(void) {
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
get_eulers(101);
for (int i = 0 ; i < cnt; i++) {
cout << i << " " << primes[i] << endl;
}
cout << endl;
// 输出1到100每个数的欧拉函数值
for (int j = 1 ; j < 101; j++) {
cout << j << " " << euler[j] << endl;
}
fclose(stdin);
fclose(stdout);
return 0;
}
翡蜀定理
定义
裴蜀定理,又称贝祖定理(Bézout's lemma)。是一个关于最大公约数的定理。
其内容是:
设 \(a,b\) 是不全为零的整数,则存在整数 \(x,y\) , 使得 \(ax+by=\gcd(a,b)\) .
证明
-
若任何一个等于 \(0\) , 则 \(\gcd(a,b)=a\) . 这时定理显然成立。
-
若 \(a,b\) 不等于 \(0\) .
由于 \(\gcd(a,b)=\gcd(a,-b)\) ,
不妨设 \(a,b\) 都大于 \(0\) , \(a\geq b,\gcd(a,b)=d\) .
对 \(ax+by=d\) , 两边同时除以 \(d\) , 可得 \(a_1x+b_1y=1\) , 其中 \((a_1,b_1)=1\) .
转证 \(a_1x+b_1y=1\) .
我们先回顾一下辗转相除法是怎么做的,由 \(\gcd(a, b) \rightarrow \gcd(b,a\mod b) \rightarrow ...\) 我们把模出来的数据叫做 \(r\) 于是,有
\[\gcd(a_1,b_1)=\gcd(b_1,r_1)=\gcd(r_1,r_2)=\cdots=(r_{n-1},r_n)=1 \]把辗转相除法中的运算展开,做成带余数的除法,得
\[\begin{aligned}a_1 &= q_1b+r_1 &(0\leq r_1<b_1) \\ b_1 &= q_2r_1+r_2 &(0\leq r_2<r_1) \\ r_1 &= q_3r_2+r_3 &(0\leq r_3<r_2) \\ &\cdots \\ r_{n-3} &= q_{n-1}r_{n-2}+r_{n-1} \\ r_{n-2} &= q_nr_{n-1}+r_n \\ r_{n-1} &= q_{n+1}r_n\end{aligned} \]不妨令辗转相除法在除到互质的时候退出则 \(r_n=1\) 所以有( \(q\) 被换成了 \(x\) ,为了符合最终形式)
\[r_{n-2}=x_nr_{n-1}+1 \]即
\[1=r_{n-2}-x_nr_{n-1} \]由倒数第三个式子 \(r_{n-1}=r_{n-3}-x_{n-1}r_{n-2}\) 代入上式,得
\[1=(1+x_nx_{n-1})r_{n-2}-x_nr_{n-3} \]然后用同样的办法用它上面的等式逐个地消去 \(r_{n-2},\cdots,r_1\) ,
可证得 \(1=a_1x+b_1y\) .
这样等于是一般式中 \(d=1\) 的情况。
应用
"Codeforces Round #290 (Div. 2) D. Fox And Jumping"
给出 \(n\) 张卡片,分别有 \(l_i\) 和 \(c_i\) 。在一条无限长的纸带上,你可以选择花 \(c_i\) 的钱来购买卡片 \(i\) ,从此以后可以向左或向右跳 \(l_i\) 个单位。问你至少花多少元钱才能够跳到纸带上全部位置。若不行,输出 \(-1\) 。
分析该问题,先考虑两个数的情况,发现想要跳到每一个格子上,必须使得这些数通过数次相加或相加得出的绝对值为 \(1\) ,进而想到了裴蜀定理。
可以推出:如果 \(a\) 与 \(b\) 互质,那么一定存在两个整数 \(x\) 与 \(y\) ,使得 \(ax+by=1\) .
由此得出了若选择的卡牌的数通过数次相加或相减得出的绝对值为 \(1\) ,那么这些数一定互质,此时可以考虑动态规划求解。
不过可以转移思想,因为这些数互质,即为 \(0\) 号节点开始,每走一步求 \(\gcd\) (节点号,下一个节点),同时记录代价,就成为了从 \(0\) 通过不断 \(\gcd\) 最后变为 \(1\) 的最小代价。
由于:互质即为最大公因数为 \(1\) , \(\gcd(0,x)=x\) 这两个定理,可以证明该算法的正确。选择优先队列优化 Dijkstra 求解。
不过还有个问题,即为需要记录是否已经买过一个卡片,开数组标记由于数据范围达到 \(10^9\) 会超出内存限制,可以想到使用 unordered_map (比普通的 map 更快地访问各个元素,迭代效率较低,详见 STL-map )
欧拉降幂

费马小定理
定理内容
假如\(p\)是质数,且\((a,p)=1\),那么 \(a^(p-1) \equiv 1(\mod p)\)
假如\(p\)是质数,且\(a,p\)互质,那么 \(a\)的\((p-1)\)次方除以\(p\)的余数恒等于\(1\)
准备知识
引理1.剩余系定理2
若\(a,b,c\)为任意3个整数,\(m\)为正整数,且\((m,c)=1\),则当\(ac\equiv bc(\mod m\))时,有\(a\equiv b(\mod m)\)
证明
\(ac\equiv bc(\mod m)\)可得\(ac–bc\equiv 0(\mod m)\)可得\((a-b)c\equiv 0(\mod m)\)
因为\((m,c)=1\)即\(m,c\)互质,\(c\)可以约去,\(a–b\equiv 0(\mod m)\)可得\(a\equiv b(\mod m)\)
引理2.剩余系定理5
若\(m\)为整数且\(m>1,a[1],a[2],a[3],a[4],…a[m]\)为\(m\)个整数,若在这\(m\)个数中任取\(2\)个整数对\(m\)不同余,则这\(m\)个整数对\(m\)构成完全剩余系。
证明
构造\(m\)的完全剩余系(\(0,1,2,...,m-1\)),所有的整数必然这些整数中的\(1\)个对模\(m\)同余。取\(r[1]=0,r[2]=1,r[3]=2,r[4]=3,...r=i-1,1<i\leq m\)。令(1):\(a[1]\equiv r[1](\mod m),a[2]\equiv r[2](\mod m),a\equiv r(\mod m)\)(顺序可以不同),因为只有在这种情况下才能保证集合\(a_1,a_2,a_3,a_4,...,a_m\)中的任意2个数不同余,否则必然有2个数同余。由式(1)自然得到集合\({a_1,a_2,a_3,a_4,…a_m}\)对\(m\)构成完全剩余系。
完全剩余系
从模\(n\)的每个剩余类中各取一个数,得到一个由\(n\)个数组成的集合,叫做模\(n\)的一个完全剩余系。完全剩余系常用于数论中存在性证明。
剩余系:由关于模m同余的数的集合,每一个集合叫做关于模m同余的剩余系
比如模5的一个剩余系:0,5,10,15…
完全剩余系:从模m的每个剩余系中各取一个数得到m的数,叫做模m的一个完全剩余系
比如模5的一个完全剩余系:0,1,2,3,4
从模n的每个剩余类中各取一个数,得到一个由n个数组成的集合,叫做模n的一个完全剩余系.例如,一个数除以4的余数只能是0,1,2,3,{0,1,2,3}和{4,5,-2,11}是模4的完全剩余系.可以看出0和4,1和5,2和-2,3和11模4同余,这4组数分别属于4个剩余类.
引理3.剩余系定理7
设\(m\)是一个整数,且\(m>1\),\(b\)是一个整数且\((m,b)=1\)。如果\(a_1,a_2,a_3,a_4,...,a_m\)是模\(m\)的一个完全剩余系,则\(ba[1],ba[2],ba[3],ba[4],…ba[m]\)也构成模\(m\)的一个完全剩余系。
证明
若存在2个整数\(ba\)和\(ba[j]\)同余即\(ba\equiv ba[j](\mod m)\),根据引理1则有\(a\equiv a[j](\mod m)\)。根据完全剩余系的定义和引理4(完全剩余系中任意2个数之间不同余,易证明)可知这是不可能的,因此不存在2个整数\(ba\)和\(ba[j]\)同余。由引理5可知\(ba[1],ba[2],ba[3],ba[4],…ba[m]\)构成模\(m\)的一个完全剩余系。
引理4.同余定理6
如果\(a,b,c,d\)是四个整数,且\(a\equiv b(\mod m),c\equiv d(\mod m)\),则有\(ac\equiv bd(\mod m)\)
证明
由题设得\(ac\equiv bc(\mod m),bc\equiv bd(\mod m)\),由模运算的传递性可得\(ac\equiv bd(\mod m)\)
证明过程
构造素数\(p\)的完全剩余系\(P={1,2,3,4…(p-1)}\),因为\((a,p)=1\),由引理3可得\(A={a,2a,3a,4a,…(p-1)a}\)也是\(p\)的一个完全剩余系。令\(W=1\times 2\times 3\times 4…\times (p-1)\),显然\(W\equiv W(\mod p)\)。令\(Y=a\times 2a\times 3a\times 4a\times ...\times (p-1)a\),因为\({a,2a,3a,4a,…(p-1)a}\)是\(p\)的完全剩余系,由引理2以及引理4可得\(a\times 2a\times 3a\times …(p-1)a\equiv 1\times 2\times 3\times …(p-1)(\mod p)\)即\(W\times a^{p-1}\equiv W(\mod p)\)。易知\((W,p)=1\),由引理1可知\(a^{p-1}\equiv 1(\mod p)\)
二次探测定理
11.排列组合
排列组合
排列组合是组合数学中的基础。排列就是指从给定个数的元素中取出指定个数的元素进行排序;组合则是指从给定个数的元素中仅仅取出指定个数的元素,不考虑排序。排列组合的中心问题是研究给定要求的排列和组合可能出现的情况总数。排列组合与古典概率论关系密切。
在高中初等数学中,排列组合多是利用列表、枚举等方法解题。
加法 & 乘法原理
加法原理
完成一个工程可以有 \(n\) 类办法, \(a_i(1 \le i \le n)\) 代表第 \(i\) 类方法的数目。那么完成这件事共有 \(S=a_1+a_2+\cdots +a_n\) 种不同的方法。
乘法原理
完成一个工程需要分 \(n\) 个步骤, \(a_i(1 \le i \le n)\) 代表第 \(i\) 个步骤的不同方法数目。那么完成这件事共有 \(S = a_1 \times a_2 \times \cdots \times a_n\) 种不同的方法。
排列与组合基础
排列数
从 \(n\) 个不同元素中,任取 \(m\) ( \(m\leq n\) , \(m\) 与 \(n\) 均为自然数,下同)个元素按照一定的顺序排成一列,叫做从 \(n\) 个不同元素中取出 \(m\) 个元素的一个排列;从 \(n\) 个不同元素中取出 \(m\) ( \(m\leq n\) ) 个元素的所有排列的个数,叫做从 \(n\) 个不同元素中取出 \(m\) 个元素的排列数,用符号 \(\mathrm A_n^m\) (或者是 \(\mathrm P_n^m\) )表示。
排列的计算公式如下:
\(n!\) 代表 \(n\) 的阶乘,即 \(6! = 1 \times 2 \times 3 \times 4 \times 5 \times 6\) 。
公式可以这样理解: \(n\) 个人选 \(m\) 个来排队 ( \(m \le n\) )。第一个位置可以选 \(n\) 个,第二位置可以选 \(n-1\) 个,以此类推,第 \(m\) 个(最后一个)可以选 \(n-m+1\) 个,得:
全排列: \(n\) 个人全部来排队,队长为 \(n\) 。第一个位置可以选 \(n\) 个,第二位置可以选 \(n-1\) 个,以此类推得:
全排列是排列数的一个特殊情况。
组合数
从 \(n\) 个不同元素中,任取 \(m\) ( \(m\leq n\) ) 个元素组成一个集合,叫做从 \(n\) 个不同元素中取出 \(m\) 个元素的一个组合;从 \(n\) 个不同元素中取出 \(m\) ( \(m\leq n\) ) 个元素的所有组合的个数,叫做从 \(n\) 个不同元素中取出 \(m\) 个元素的组合数。用符号 \(\mathrm C_n^m\) 来表示。
组合数计算公式
如何理解上述公式?我们考虑 \(n\) 个人 \(m\) ( \(m \le n\) ) 个出来,不排队,不在乎顺序 \(C_n^m\) 。如果在乎排列那么就是 \(A_n^m\) ,如果不在乎那么就要除掉重复,那么重复了多少?同样选出的来的 \(m\) 个人,他们还要“全排”得 \(A_n^m\) ,所以得:
组合数也常用 \(\displaystyle \binom{n}{m}\) 表示,读作「 \(n\) 选 \(m\) 」,即 \(\displaystyle \mathrm C_n^m=\binom{n}{m}\) 。实际上,后者表意清晰明了,美观简洁,因此现在数学界普遍采用 \(\displaystyle \binom{n}{m}\) 的记号而非 \(\mathrm C_n^m\) 。
组合数也被称为「二项式系数」,下文二项式定理将会阐述其中的联系。
特别地,规定当 \(m>n\) 时, \(\mathrm A_n^m=\mathrm C_n^m=0\) 。
组合数的递归写法
\(f[i][j]\)表示\(C_j^i\),则$$f[i][j]=f[i-1][j-1]+f[i-1][j]$$
边界条件是\(f[i][j]=1(j=1||i=j)\)
二项式定理
在进入排列组合进阶篇之前,我们先介绍一个与组合数密切相关的定理——二项式定理。
二项式定理阐明了一个展开式的系数:
证明可以采用数学归纳法,利用 \(\displaystyle \binom{n}{k}+\binom{n}{k-1}=\binom{n+1}{k}\) 做归纳。
二项式定理也可以很容易扩展为多项式的形式:
设 n 为正整数, \(x_i\) 为实数,
其中的 \(\binom{n}{n_1n_2\cdots n_t}\) 是多项式系数,它的性质也很相似:
来自lzw的博客——二项式定理
公式$$(x+y)n=\sum\limits_{k=0}nCn_{k}xyk=\sum\limits_{k=0}nCn_{k}xy^{n-k}$$
是二项式公式,其中$$C^n_k=\dfrac{n!}{k!(n-k)!}$$
公式也可以写作$$(x+y)n=Cn_0xny0+Cn_1xy1+Cn_2x{n-2}y2+...+Cn_{n-1}x1y{n-1}+Cn_nx0yn$$
二项式系数是\(C^k_n\),\(C^k_nx^{n-k}y^k\)是展开式中的第\(k+1\)项,可记作\(T_{k+1}=C^k_nx^{n-k}y^k\)
如果\(y=1\),则\((1+x)^n=1+C^1_nx+C_n^2x^2+...+C^n_nx^n\)
排列与组合进阶篇
接下来我们介绍一些排列组合的变种。
多重集的排列数 | 多重组合数
请大家一定要区分 多重组合数 与 多重集的组合数 !两者是完全不同的概念!
多重集是指包含重复元素的广义集合。设 \(S=\{n_1\cdot a_1,n_2\cdot a_2,\cdots,n_k\cdot a_k,\}\) 表示由 \(n_1\) 个 \(a_1\) , \(n_2\) 个 \(a_2\) ,…, \(n_k\) 个 \(a_k\) 组成的多重集, \(S\) 的全排列个数为
相当于把相同元素的排列数除掉了。具体地,你可以认为你有 \(k\) 种不一样的球,每种球的个数分别是 \(n_1,n_2,\cdots,n_k\) ,且 \(n=n_1+n_2+\ldots+n_k\) 。这 \(n\) 个球的全排列数就是 多重集的排列数 。多重集的排列数常被称作 多重组合数 。我们可以用多重组合数的符号表示上式:
可以看出, \(\displaystyle \binom{n}{m}\) 等价于 \(\displaystyle \binom{n}{m,n-m}\) ,只不过后者较为繁琐,因而不采用。
多重集的组合数 1
设 \(S=\{n_1\cdot a_1,n_2\cdot a_2,\cdots,n_k\cdot a_k,\}\) 表示由 \(n_1\) 个 \(a_1\) , \(n_2\) 个 \(a_2\) ,…, \(n_k\) 个 \(a_k\) 组成的多重集。那么对于整数 \(r(r<n_i,\forall i\in[1,k])\) ,从 \(S\) 中选择 \(r\) 个元素组成一个多重集的方案数就是 多重集的组合数 。这个问题等价于 \(x_1+x_2+\cdots+x_k=r\) 的非负整数解的数目,可以用插板法解决,答案为
多重集的组合数 2
考虑这个问题:设 \(S=\{n_1\cdot a_1,n_2\cdot a_2,\cdots,n_k\cdot a_k,\}\) 表示由 \(n_1\) 个 \(a_1\) , \(n_2\) 个 \(a_2\) ,…, \(n_k\) 个 \(a_k\) 组成的多重集。那么对于正整数 \(r\) ,从 \(S\) 中选择 \(r\) 个元素组成一个多重集的方案数。
这样就限制了每种元素的取的个数。同样的,我们可以把这个问题转化为带限制的线性方程求解:
于是很自然地想到了容斥原理。容斥的模型如下:
- 全集: \(\displaystyle \sum_{i=1}^kx_i=r\) 的非负整数解。
- 属性: \(x_i\le n_i\) 。
于是设满足属性 \(i\) 的集合是 \(S_i\) , \(\overline{S_i}\) 表示不满足属性 \(i\) 的集合,即满足 \(x_i\ge n_i+1\) 的集合。那么答案即为
根据容斥原理,有:
拿全集 \(\displaystyle |U|=\binom{k+r-1}{k-1}\) 减去上式,得到多重集的组合数
其中 A 是充当枚举子集的作用,满足 \(|A|=p,\ A_i<A_{i+1}\) 。
不相邻的排列
\(1 \sim n\) 这 \(n\) 个自然数中选 \(k\) 个,这 \(k\) 个数中任何两个数不相邻数的组合有 \(\displaystyle \binom {n-k+1}{k}\) 种。
错位排列
我们把错位排列问题具体化,考虑这样一个问题:
\(n\) 封不同的信,编号分别是 \(1,2,3,4,5\) ,现在要把这 5 封信放在编号 \(1,2,3,4,5\) 的信封中,要求信封的编号与信的编号不一样。问有多少种不同的放置方法?
假设我们考虑到第 \(n\) 个信封,初始时我们暂时把第 n 封信放在第 n 个信封中,然后考虑两种情况的递推:
- 前面 \(n-1\) 个信封全部装错;
- 前面 \(n-1\) 个信封有一个没有装错其余全部装错。
对于第一种情况,前面 \(n-1\) 个信封全部装错:因为前面 \(n-1\) 个已经全部装错了,所以第 n 封只需要与前面任一一个位置交换即可,总共有 \(f(n-1)\times (n-1)\) 种情况。
对于第二种情况,前面 \(n-1\) 个信封有一个没有装错其余全部装错:考虑这种情况的目的在于,若 \(n-1\) 个信封中如果有一个没装错,那么我们把那个没装错的与 \(n\) 交换,即可得到一个全错位排列情况。
其他情况,我们不可能通过一次操作来把它变成一个长度为 n 的错排。
于是可得错位排列的递推式为 \(f(n)=(n-1)(f(n-1)+f(n-2))\) 。
错位排列数列的前几项为 \(0,1,2,9,44,265\) 。
圆排列
\(n\) 个人全部来围成一圈,所有的排列数记为 \(\mathrm Q_n^n\) 。考虑其中已经排好的一圈,从不同位置断开,又变成不同的队列。
所以有
由此可知部分圆排列的公式:
组合数性质 | 二项式推论
由于组合数在 OI 中十分重要,因此在此介绍一些组合数的性质。
相当于将选出的集合对全集取补集,故数值不变。(对称性)
由定义导出的递推式。
组合数的递推式(杨辉三角的公式表达)。我们可以利用这个式子,在 \(O(n^2)\) 的复杂度下推导组合数。
这是二项式定理的特殊情况。取 \(a=b=1\) 就得到上式。
二项式定理的另一种特殊情况,可取 \(a=1, b=-1\) 。
拆组合数的式子,在处理某些数据结构题时会用到。
这是 \((6)\) 的特殊情况,取 \(n=m\) 即可。
带权和的一个式子,通过对 \((3)\) 对应的多项式函数求导可以得证。
与上式类似,可以通过对多项式函数求导证明。
可以通过组合意义证明,在恒等式证明中较常用。
通过定义可以证明。
其中 \(F\) 是斐波那契数列。
通过组合分析——考虑 \(S={a_1, a_2, \cdots, a_{n+1}}\) 的 \(k+1\) 子集数可以得证。
卡特兰数
卡特兰数是一个数列,递推公式如下:
设\(h_n\)为catalan数的第\(n\)项,令\(h_0=1,h_1=1\),则catalan数满足递推式:
catalan数的其他推导:\(C^y_x=C(x,y)=\dfrac{x!}{(x-y)!y!}\)
以下问题属于 Catalan 数列:
- 有 \(2n\) 个人排成一行进入剧场。入场费 5 元。其中只有 \(n\) 个人有一张 5 元钞票,另外 \(n\) 人只有 10 元钞票,剧院无其它钞票,问有多少中方法使得只要有 10 元的人买票,售票处就有 5 元的钞票找零?
- 一位大城市的律师在她住所以北 \(n\) 个街区和以东 \(n\) 个街区处工作。每天她走 \(2n\) 个街区去上班。如果他从不穿越(但可以碰到)从家到办公室的对角线,那么有多少条可能的道路?
- 在圆上选择 \(2n\) 个点,将这些点成对连接起来使得所得到的 \(n\) 条线段不相交的方法数?
- 对角线不相交的情况下,将一个凸多边形区域分成三角形区域的方法数?
- 一个栈(无穷大)的进栈序列为 \(1,2,3, \cdots ,n\) 有多少个不同的出栈序列?
- \(n\) 个结点可够造多少个不同的二叉树?
- \(n\) 个不同的数依次进栈,求不同的出栈结果的种数?
- \(n\) 个 \(+1\) 和 \(n\) 个 \(-1\) 构成 \(2n\) 项 \(a_1,a_2, \cdots ,a_{2n}\) ,其部分和满足 \(a_1+a_2+ \cdots +a_k \geq 0(k=1,2,3, \cdots ,2n)\) 对与 \(n\) 该数列为?
其对应的序列为:
| \(H_0\) | \(H_1\) | \(H_2\) | \(H_3\) | \(H_4\) | \(H_5\) | \(H_6\) | ... |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 5 | 14 | 42 | 132 | ... |
(Catalan 数列)
递推式
该递推关系的解为:
关于 Catalan 数的常见公式:
例题洛谷 P1044 栈"
题目大意:入栈顺序为 \(1,2,\ldots ,n\) ,求所有可能的出栈顺序的总数。
#include <iostream>
using namespace std;
int n;
long long f[25];
int main() {
f[0] = 1;
cin >> n;
for (int i = 1; i <= n; i++) f[i] = f[i - 1] * (4 * i - 2) / (i + 1);
// 这里用的是常见公式2
cout << f[n] << endl;
return 0;
}
路径计数问题
非降路径是指只能向上或向右走的路径。
-
从 \((0,0)\) 到 \((m,n)\) 的非降路径数等于 \(m\) 个 \(x\) 和 \(n\) 个 \(y\) 的排列数,即 \(\dbinom{n + m}{m}\) 。
-
从 \((0,0)\) 到 \((n,n)\) 的除端点外不接触直线 \(y=x\) 的非降路径数:
先考虑 \(y=x\) 下方的路径,都是从 \((0, 0)\) 出发,经过 \((1, 0)\) 及 \((n, n-1)\) 到 \((n,n)\) ,可以看做是 \((1,0)\) 到 \((n,n-1)\) 不接触 \(y=x\) 的非降路径数。
所有的的非降路径有 \(\dbinom{2n-2}{n-1}\) 条。对于这里面任意一条接触了 \(y=x\) 的路径,可以把它最后离开这条线的点到 \((1,0)\) 之间的部分关于 \(y=x\) 对称变换,就得到从 \((0,1)\) 到 \((n,n-1)\) 的一条非降路径。反之也成立。从而 \(y=x\) 下方的非降路径数是 \(\dbinom{2n-2}{n-1} - \dbinom{2n-2}{n}\) 。根据对称性可知所求答案为 \(2\dbinom{2n-2}{n-1} - 2\dbinom{2n-2}{n}\) 。
-
从 \((0,0)\) 到 \((n,n)\) 的除端点外不穿过直线 \(y=x\) 的非降路径数:
用类似的方法可以得到: \(\dfrac{2}{n+1}\dbinom{2n}{n}\)
斯特林数
第一类斯特林数(Stirling Number)
第一类斯特林数 (斯特林轮换数) \(\begin{bmatrix}n\\ k\end{bmatrix}\) 表示将 \(n\) 个两两不同的元素,划分为 \(k\) 个非空圆排列的方案数。
递推式
边界是 \(\begin{bmatrix}n\\ 0\end{bmatrix}=[n=0]\) 。
该递推式的证明可以考虑其组合意义。
我们插入一个新元素时,有两种方案:
- 将该新元素置于一个单独的圆排列中,共有 \(\begin{bmatrix}n-1\\ k-1\end{bmatrix}\) 种方案;
- 将该元素插入到任何一个现有的圆排列中,共有 \((n-1)\begin{bmatrix}n-1\\ k\end{bmatrix}\) 种方案。
根据加法原理,将两式相加即可得到递推式。
第二类斯特林数(Stirling Number)
第二类斯特林数 (斯特林子集数) \(\begin{Bmatrix}n\\ k\end{Bmatrix}\) 表示将 \(n\) 个两两不同的元素,划分为 \(k\) 个非空子集的方案数。
递推式
边界是 \(\begin{Bmatrix}n\\ 0\end{Bmatrix}=[n=0]\) 。
还是考虑组合意义来证明。
我们插入一个新元素时,有两种方案:
- 将新元素单独放入一个子集,有 \(\begin{Bmatrix}n-1\\ k-1\end{Bmatrix}\) 种方案;
- 将新元素放入一个现有的非空子集,有 \(k\begin{Bmatrix}n-1\\ k\end{Bmatrix}\) 种方案。
根据加法原理,将两式相加即可得到递推式。
应用
上升幂与普通幂的相互转化
我们记上升阶乘幂 \(x^{\overline{n}}=\prod_{k=0}^{n-1} (x+k)\) 。
则可以利用下面的恒等式将上升幂转化为普通幂:
如果将普通幂转化为上升幂,则有下面的恒等式:
下降幂与普通幂的相互转化
我们记下降阶乘幂 \(x^{\underline{n}}=\dfrac{x!}{(x-n)!}=\prod_{k=0}^n-1 (x-k)\) 。
则可以利用下面的恒等式将普通幂转化为下降幂:
如果将下降幂转化为普通幂,则有下面的恒等式:
贝尔数
贝尔数以埃里克·坦普尔·贝尔命名,是组合数学中的一组整数数列,开首是 ( OEIS A000110 ):
\(B_n\) 是基数为 \(n\) 的集合的划分方法的数目。集合 \(S\) 的一个划分是定义为 \(S\) 的两两不相交的非空子集的族,它们的并是 \(S\) 。例如 \(B_3 = 5\) 因为 3 个元素的集合 \({a, b, c}\) 有 5 种不同的划分方法:
\(B_0\) 是 1 因为空集正好有 1 种划分方法。
公式
贝尔数适合递推公式:
证明:
\(B_{n+1}\) 是含有 \(n+1\) 个元素集合的划分个数,设 \(D_n\) 的集合为 \(\{b_1,b_2,b_3,\dots,b_n\}\) , \(D_{n+1}\) 的集合为 \(\{b_1,b_2,b_3,\dots,b_n,b_{n+1}\}\) ,那么可以认为 \(D_{n+1}\) 是有 \(D_{n}\) 增添了一个 \(b_{n+1}\) 而产生的,考虑元素 \(b_{n+1}\) 。
假如它被单独分到一类,那么还剩下 \(n\) 个元素,这种情况下划分数为 \(\binom{n}{n}B_{n}\) ;
假如它和某 1 个元素分到一类,那么还剩下 \(n-1\) 个元素,这种情况下划分数为 \(\binom{n}{n-1}B_{n-1}\) ;
假如它和某 2 个元素分到一类,那么还剩下 \(n-2\) 个元素,这种情况下划分数为 \(\binom{n}{n-2}B_{n-2}\) ;
以此类推就得到了上面的公式。
每个贝尔数都是相应的第二类 斯特林数 的和。
因为第二类斯特林数是把基数为 \(n\) 的集合划分为正好 \(k\) 个非空集的方法数目。
贝尔三角形
用以下方法构造一个三角矩阵(形式类似杨辉三角形):
- 第一行第一项为 1 \((a_{1,1}=1)\) ;
- 对于 \(n>1\) ,第 \(n\) 行第一项等于第 \(n-1\) 行的第一项 \((a_{n,1}=a_{n-1,n-1})\) ;
- 对于 \(m,n>1\) ,第 \(n\) 行的第 \(m\) 项等于它左边和左上角两个数之和 \((a_{n,m}=a_{n,m-1}+a_{n-1,m-1})\)
部分结果如下:
每行的首项是贝尔数。可以利用这个三角形来递推求出 Bell 数。
代码
```c++
const int maxn = 2000 + 5;
int bell[maxn][maxn];
void f(int n) {
bell[1][1] = 1;
for (int i = 2; i <= n; i++) {
bell[i][1] = bell[i - 1][i - 1];
for (int j = 2; j <= i; j++)
bell[i][j] = bell[i - 1][j - 1] + bell[i][j - 1];
}
}
```
12.斐波那契数列
斐波那契数列(The Fibonacci sequence, OEIS A000045 )的定义如下:
该数列的前几项如下:
性质
斐波那契数列拥有许多有趣的性质,这里列举出一部分简单的性质:
- 卡西尼性质(Cassini's identity): \(F_{n-1} F_{n+1} - F_n^2 = (-1)^n\) 。
- 附加性质: \(F_{n+k} = F_k F_{n+1} + F_{k-1} F_n\) 。
- 取上一条性质中 \(k = n\) ,我们得到 \(F_{2n} = F_n (F_{n+1} + F_{n-1})\) 。
- 由上一条性质可以归纳证明, \(\forall k\in \mathbb{N},F_n|F_{nk}\) 。
- 上述性质可逆,即 \(\forall F_a|F_b,a|b\) 。
- GCD 性质: \((F_m, F_n) = F_{(m, n)}\) 。
- 以斐波那契数列相邻两项作为输入会使欧几里德算法达到最坏复杂度(具体参见 维基 - 拉梅 )。
斐波那契编码
我们可以利用斐波那契数列为正整数编码。根据 齐肯多夫定理 ,任何自然数 \(n\) 可以被唯一地表示成一些斐波那契数的和:
并且 \(k_1 \ge k_2 + 2,\ k_2 \ge k_3 + 2,\ \ldots,\ k_r \ge 2\) (即不能使用两个相邻的斐波那契数)
于是我们可以用 \(d_0 d_1 d_2 \dots d_s 1\) 的编码表示一个正整数,其中 \(d_i=1\) 则表示 \(F_{i+2}\) 被使用。编码末位我们强制给它加一个 1(这样会出现两个相邻的 1),表示这一串编码结束。举几个例子:
给 \(n\) 编码的过程可以使用贪心算法解决:
- 从大到小枚举斐波那契数 \(F_i\) ,直到 \(F_i\le n\) 。
- 把 \(n\) 减掉 \(F_i\) ,在编码的 \(i-2\) 的位置上放一个 1(编码从左到右以 0 为起点)。
- 如果 \(n\) 为正,回到步骤 1。
- 最后在编码末位添加一个 1,表示编码的结束位置。
解码过程同理,先删掉末位的 1,对于编码为 1 的位置 \(i\) (编码从左到右以 0 为起点),累加一个 \(F_{i+2}\) 到答案。最后的答案就是原数字。
斐波那契数列通项公式
第 \(n\) 个斐波那契数可以在 \(\Theta (n)\) 的时间内使用递推公式计算。但我们仍有更快速的方法计算。
解析解
解析解即公式解。我们有斐波那契数列的通项公式(Binet's Formula):
这个公式可以很容易地用归纳法证明,当然也可以通过生成函数的概念推导,或者解一个方程得到。
当然你可能发现,这个公式分子的第二项总是小于 \(1\) ,并且它以指数级的速度减小。因此我们可以把这个公式写成
这里的中括号表示取离它最近的整数。
这两个公式在计算的时侯要求极高的精确度,因此在实践中很少用到。但是请不要忽视!结合模意义下二次剩余和逆元的概念,在 OI 中使用这个公式仍是有用的。
矩阵形式
斐波那契数列的递推可以用矩阵乘法的形式表达:
设 \(P = \begin{bmatrix}0 & 1 \cr 1 & 1 \cr\end{bmatrix}\) ,我们得到
于是我们可以用矩阵乘法在 \(\Theta(\log n)\) 的时间内计算斐波那契数列。此外,前一节讲述的公式也可通过矩阵对角化的技巧来得到。
快速倍增法
使用上面的方法我们可以得到以下等式:
于是可以通过这样的方法快速计算两个相邻的斐波那契数(常数比矩乘小)。代码如下,返回值是一个二元组 \((F_n,F_{n+1})\) 。
pair<int, int> fib(int n) {
if (n == 0) return {0, 1};
auto p = fib(n >> 1);
int c = p.first * (2 * p.second - p.first);
int d = p.first * p.first + p.second * p.second;
if (n & 1)
return {d, c + d};
else
return {c, d};
}
模意义下周期性
考虑模 \(p\) 意义下的斐波那契数列,可以容易地使用抽屉原理证明,该数列是有周期性的。考虑模意义下前 \(p^2+1\) 个斐波那契数对(两个相邻数配对):
\(p\) 的剩余系大小为 \(p\) ,意味着在前 \(p^2+1\) 个数对中必有两个相同的数对,于是这两个数对可以往后生成相同的斐波那契数列,那么他们就是周期性的。
事实上,我们有一个远比它要强的结论。模 \(n\) 意义下斐波那契数列的周期被称为 皮萨诺周期 ( OEIS A001175 ),该数可以证明总是不超过 \(6n\) ,且只有在满足 \(n=2\times 5^k\) 的形式时才取到等号。
本页面主要译自博文 Числа Фибоначчи 与其英文翻译版 Fibonacci Numbers 。其中俄文版版权协议为 Public Domain + Leave a Link;英文版版权协议为 CC-BY-SA 4.0。
来自OI-Wiki(github).
13.秦九韶算法
一般地,一元\(n\)次多项式的求值需要经过\(\dfrac{(n+1)\times n}{2}\)次乘法和\(n\)次加法,而秦九韶算法只需要\(n\)次乘法和\(n\)次加法。在人工计算时,一次大大简化了运算过程。
把一个\(n\)次多项式,改写成如下形式:
\(f(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0\)
则
\(f(x)\)
\(=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0\)
\(=(a_nx^{n-1}+a_{n-1}x^{n-2}+...a_2x+a_1)x+a_0\)
\(=((a_nx^{n-2}+a_{n-1}x^{n-3}+...+a_3x+a_2)x+a_1)x+a_0\)
\(=...\)
求多项式的值时,首先计算最内层括号内一次多项式的值,即
\(v_1=a_n*x+a_{n-1}\)
然后由内向外逐层计算一次多项式的值,即
\(v_2=v_1x+a_{n-2}\)
\(v_3=v_2x+a_{n-3}\)
...
\(v_n=v_{n-1}x+a_0\)
这样,求\(n\)次多项式\(f(x)\)的值就转化为求\(n\)个一次多项式的值。
结论:对于一个\(n\)次多项式,至多做\(n\)次乘法和\(n\)次加法。
inline double f(double x){
//秦九昭公式求多项式
double u[20];
u[n] = a[n];
for(int i=n-1;i>=0;--i)
u[i] = u[i+1]*x+a[i];
return u[0];
}
double check(double x){
double dx = eps;
double dy = f(x+dx)-f(x);
return dy/dx;
}
14.错排问题
例题 LGP1595 信封问题
某人写了\(n\)封信和\(n\)个信封,如果所有的信都装错了信封,求所有信都装错信封,共有多少种不同情况?
题解
令\(f_n\)表示\(n\)封信错排的答案为多少,思考\(f_n\)的递推式。
- 第1封信放在第\(k\)个信封,第\(k\)封信放在第1个信封里面。
这样我们就确定了两个新的位置,剩下的就是\(n-2\)封信的错排问题,我们递归解决就可以了。 - 第1封信放在第\(k\)个信封,第\(k\)封信不放在第1个信封里面。
此时我们可以把第\(k\)封信重新编号为第1封信,这样他就真的不能放到第1个信封里面了。此时是\(n-1\)个信封的错排问题。
讨论之后我们发现对于每种情况,\(k\)有\(n-1\)种取值,于是我们可以得出递推公式
15.自然数拆分
题面
任何一个大于\(1\)的自然数\(n\),总可以拆分成若干小于\(n\)的自然数之和,求出\(n\)的所有拆分.
题解
用数组\(a\)储存完成\(n\)的一种拆分,不完全归纳法的分析可知当\(n=7\)时,按照\(a[1]\)分类,有\(a[1]=1,a[1]=2,...,a[1]=\dfrac{n}{2}\),共\(\dfrac{n}{2}\)大类拆分。在每一类拆分时,\(a[1]=i,a[2]=n-i\),从\(x=2\),继续拆分从\(a[x]\)开始,\(a[x]\)能否拆分取决于\(\dfrac{a[x]}{2}\)是否大于等于\(a[x-1]\)。递归过程的参数\(t\)指向要拆分的数\(a[x]\)。
#include <cstdio>
#include <algorithm>
using namespace std;
void dfs(int t){
int i,j,k;
printf("%d=%d",n,a[1]);
for(i=2;i<=t;i++){
printf("+%d",a[i]);
}
printf("\n");
j=t;k=a[j];
for(i=a[j-1];i<=k/2;i++){
a[j]=i;
a[j+1]=k-i;
}
}
int main(){
int i,j,k;
scanf("%d",&n);
for(i=1;i<=n/2;i++){
a[1]=i;
a[2]=n-i;
dfs(2);
}
16.中位数性质
JSK43512
https://nanti.jisuanke.com/t/43512
给出\(n\)个相邻酒桶在坐标轴的位置,要求通过移动一些酒桶,使得每个酒桶之间的距离为\(k\)。
求最小移动距离
(另外这题评测机跑的飞快,你可以认为 1s 1e8)
\(1\le N,K\le 10^6\)
题解
我们设原始位置为 \(x\),第一个啤酒摊位置为\(a\),将其排序。某一油桶\(i\)位置是\(x_i\),它移动的距离是位置与它本来应该在的位置\(a+k(i-1)\)的差值,我们可以得到:
通过移项,得到:
通过预处理\(c_i=x_i-k(i-1)\),式子变形成为:
则转化到了:数轴上存在\(c_i\)的点,寻找一个点a使得ans最小,根据定理可知,a为c的中位数时ans有最小值。
结论
定理:给定数轴上的\(n\)个点,求一个到他们的距离之和尽量小的点。
结论是:这个点是这\(n\)个数的中位数。所以只需排序即可。严谨的证明如下:
在数轴上标出这\(n\)个点,假定数轴上标好了六个点,从左到右编号\(C_i(i\in {1,2,3,4,5,6})\),如果选定\(C_4,C_5\)之间的一点\(\text P\),之后把这个点向左(或者向右,效果相同,假定向左)\(D\)个单位长度,则\(\text P′\)到它左边的四个点距离减少了\(4D\),到右边的两个点距离增加了\(2D\),总的来说距离减小了\(2D\)。
通过这样的移动,发现在奇数个数构成的数列,满足条件的数是最中间的数,而偶数个数构成的数列是最中间两个数的平均数,得证。
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#define ll long long
using namespace std;
const int N=1e6+7;
ll n,k;
ll arr[N],c[N];
int main()
{
scanf("%lld %lld",&n,&k);
for(int i = 1;i <= n;i ++){
scanf("%lld",&arr[i]);
}
sort(arr+1,arr+1+n);
for(int i = 1;i <= n;i ++) c[i] = arr[i] - k*(i-1);
sort(c+1,c+1+n);
ll ans = c[(1+n)/2];
if(n%2==0) ans = (c[n/2]+c[n/2+1])/2;
ll sum = 0;
for(int i = 1;i <= n;i ++){
sum += abs(ans-c[i]);
}
printf("%lld",sum);
return 0;
}
// by whh
T112394 分金币
题目描述
圆桌周围坐了\(n\)个人,每个人有一定数量的金币,金币的总数保证是\(n\)的倍数,每个人可以向左或向右给出一些金币,使得最终每个人的金币数相等。你的任务是求出被转移了的金币的总数。
比如,\(n=4\)时,如果四个人的金币数是\(1,2,5,4\),则转移4枚金币(第3个人给第2个人2枚,第2个人和第4个人分别给第1个人1枚金币)即可达到目的。
输入格式
包含多组数据。第一行是测试组数\(T\),接下来每组数据第一行为一个整数\(n\),以下\(n\)行每行为一个整数,按逆时针顺序给出每个人拥有的金币数。
输出格式
对于每组数据,输出被转手金币数量的最小值,输入保证这个值不超过64位无符号整数范围。
输入输出样例
输入
2
3
100
100
100
4
1
2
5
4
输出
0
4
说明/提示
\(1\leq T \leq 10, n\leq 10^6\)
标程时间复杂度:\(O(Tnlogn)\)
题解
对于在座的\(n\)个人,记每个人现在拥有的金币数是\(A_i(i\in [1,n])\),则金币总数\(s=\sum^{n}_{i=1}A_i\),每个人最终得到的金币数$$y=\frac{s}{n}$$
如果1号给2号1枚,而2号给1号2枚,就相当于2号给1号1枚,所以我们用\(x_2\)表示2号给1号了多少金币,特别地,如果\(x_2<0\),实际上是1号给2号\(-x_2\)枚金币。注意,由于是环形,所以\(x_1\)表示1号给\(n\)号了几枚金币。
如果有四个人,依次编号\(1,2,3,4\),对于1号来说,他给了4号\(x_1\)枚金币,但是2号又给了他\(x_2\)枚,我们最终得到1号最终的金币数$$y=A_1-x_1+x_2$$
同理,对于第2个人,有\(y=A_2-x_2+x_3\),我们一共得到了\(n\)个方程,很可惜,我们不能解,因为前\(n-1\)个式子能推导出第\(n\)个,所以只有\(n-1\)个式子是有用的。
尽管这样,我们还是想用\(x_1\)来表示其他的\(x_i\),有:对于第1个人,\(A_1-x_1+x_2=y\),于是$$x_2=y-A_1+x_1=x_1-C_1$$
其中我们规定:$$C_i=A_i-y$$则\(C_1=A_1-y\)
对于第2个人,\(A_2-x_2+x_3=y\),于是$$x_3=y-A_2+x_2=2y-A_1-A_2+x_1=x_1-C_2$$
对于第2个人,\(A_3-x_3+x_4=y\),于是$$x_4=y-A_3+x_3=3y-A_1-A_2-A_3+x_1=x_1-C_3$$
如此推导下去,我们可以得到若干等式。我们的目的是计算所有\(x_i\)的绝对值之和最小,即:$$(|x_1|+|x_1-C_1|+|x_1-C_2|+...+|x_1-C_{n-1}|)_{\min}$$
注意\(|x_i-C_i|\)的几何意义是数轴上点\(x_i\)到\(C_i\)的距离,问题变成了:给定数轴上的\(n\)个点,求一个到他们的距离之和尽量小的点。
结论是:这个点是这\(n\)个数的中位数。所以只需排序即可。严谨的证明如下:
在数轴上标出这\(n\)个点,假定数轴上标好了六个点,从左到右编号\(C_i(i\in \{1,2,3,4,5,6\})\),如果选定\(C_4,C_5\)之间的一点\(P\),之后把这个点向左(或者向右,效果相同,假定向左)\(D\)个单位长度,则\(P'\)到它左边的四个点距离减少了\(4D\),到右边的两个点距离增加了\(2D\),总的来说距离减小了\(2D\)。
通过这样的移动,发现在奇数个数构成的数列,满足条件的数是最中间的数,而偶数个数构成的数列是最中间两个数的平均数,得证。
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
using namespace std;
const int maxn=1000000+10;
long long A[maxn],C[maxn],tot,M;
int T;
int n;
int main(){
//freopen("coin10.in","r",stdin);
//freopen("coin10.out","w",stdout);
scanf("%d",&T);
while(T--){
scanf("%d",&n);
tot=0;
memset(A,0,sizeof(A));
memset(C,0,sizeof(C));
for(int i=1;i<=n;i++){
scanf("%lld",&A[i]);
tot+=A[i];
}
M=tot/n;
C[0]=0;
for(int i=1;i<n;i++){
C[i]=C[i-1]+A[i]-M;
}
sort(C,C+n);
long long x1=C[n/2],ans=0;
for(int i=0;i<n;i++){
ans+=abs(x1-C[i]);
}
printf("%lld\n",ans);
}
return 0;
}
17.进制转换
基本思路
先将\(x\)进制的某数转换为十进制,运用:
\((abcd)_x=(x^3a+x^2b+xc+d)_{10}\)
的转换
然后再将该数转换为对应的\(y\)进制,使用相除取余法,结果存入数组倒序输出
代码
char数组一定要在主程序之外开,要不然输出很奇怪(教训)
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <cstring>
using namespace std;
char s[205];
int main (){
int x,y;
scanf("%d%d",&x,&y);
scanf("%s",s);
printf("(%s)%d=(",s,x);
int len;
len=strlen(s);
int ans=0;
for(int i=len-1;i>=0;i--){
ans+=(s[i]-'0')*pow(x,i);
}
printf("%d)10=(",ans);
int a[210];
int j=1;
while(ans/y!=0){
a[j]=ans%y;
ans=ans/y;
j++;
}
a[j]=ans;
for(int i=j;i>=1;i--){
printf("%d",a[i]);
}
printf(")%d\n",y);
return 0;
}
18.期望与概率
(1)期望的定义
每次可能结果的概率乘以其结果的总和
(2)期望的性质
\(X\)是随机变量,\(C\)是常数,则\(E(CX)=C\times E(X)\)
证明:设\(X\)的多个随机变量(即能取到的数值为)\(\{{a_{i}}\}\),对应出现概率为\(p_i\),则求期望的式子是:
而随机变量变为\(CX\),即\(\{Ca_i\}\)时,求解式子变为:
以下式子证明类似:
- 设\(X,Y\)是任意两个随机变量,则有\(E(X+Y)=E(X)+E(Y)\)
- 设\(X,Y\)是两个相互独立的随机变量,有\(E(XY)=E(X)E(Y)\)
- 设\(C\)为常数,有\(E(C)=C\)
(3)期望与均值
比如掷骰子的均值,计算方法:
【你必须亲自掷骰子,然后才能知道,比如】
而期望无需亲自操作 如:
该数值恒定
在对多个均值求均值后,两者就无限接近了。
(4)例题1
题面
甲乙两人赌博,丙作为裁判,五局三胜,赢的人可以获得100元,比赛进行到第四局的时候甲胜了2局,乙胜了1局,但这时赌场遇到了查封,丙逃走。这时甲乙应该如何分配100元?(每局一定有胜负)
A 平分
A胜利更多,已经拿到赛点。他显然不愿意
B 按照获胜的比例
继续进行一轮的话,
50%:甲赢了,拿走100元。
50%:乙赢了,继续比赛。
那如果下一局乙赢了,接下来两人又有50%的概率获胜,都可能拿走100元,还咋分?
C 学会期望的人应该这样做(吧)
假设甲最终输了,那么他是在什么概率下输的呢?
\(\dfrac{1}{2}\times \dfrac{1}{2}=\dfrac{1}{4}\)
他实际上只有四分之一的概率输。
显而易见,因为每局都能分出胜负,所以他有 \(\dfrac{3}{4}\)的概率赢掉。
那么情况就简单了,我们根据他们的胜率来分钱。
甲分 \(100\times \dfrac{3}{4}=75\)
乙分 \(100\times \dfrac{1}{4}=25\)
(5)例题2
题面
已知3个红包中有一个1000元的,两个500元的。
抽取了一个后,随机打开剩下红包中的一个,里面装着500元钱。
询问:如果同意你们用手上的红包换取未打开的红包,你会换吗?
题解
下面定量计算一下:
设为\(A,B,C\)三个红包
当员工选择了\(A\)红包后,就将三个红包分为两组,第一组为\(A\)红包,第二组为\(B,C\)红包。很明显1000元在第一组的概率为 \(\dfrac{1}{3}\),在第二组的概率为 \(\dfrac{2}{3}\),而面试官打开了B红包,发现B为500元红包,这里其实是帮助员工在第二组里筛选掉了一个错误答案,所以1000元在C红包的概率其实为 \(\dfrac{2}{3}\)。
所以就要换喽
(6)例题3
设一张彩票为2元,每售1000000张开奖,假设中奖号码为 342356,则每张彩票有一个对应的六位数号码,奖次如下:(中奖不叠加)
末位相等,安慰奖:奖励4元,中奖概率0.1
后两位相等,幸运奖:奖励20元,中奖概率0.01
后三位相等,手气奖:奖励200元,中奖概率0.001
后四位相等,一等奖:奖励2000元,中奖概率0.0001
后五位相等,特等奖:奖励20000元,中奖概率0.00001
我们来用简单的概率知识来计算一下,对于每一位购买彩票的用户,公司可能支出为:
\(0.1\times 4+0.01\times 20+0.001\times 200+0.0001\times 2000+0.00001\times 20000=1.2\)
也就是说,公司期望对每个人赚0.8元。
每1000000张,就是800000元!
如果6位均相等,给200000元的话,公司会少赚200000元!!(可以计算一下)
(7)例题4
题面
抛一枚硬币,如果是反面就继续抛,问抛 出正面的期望次数。 ]
(期望话可以理解为概率\(\times\)代价, 比如说小A投球中的概率为\(\dfrac{1}{3}\),那么投三 个球中的期望就是\(\dfrac{1}{3}\times 3=1\))
题解
\(x=1+\dfrac{1}{2}\times 0+\dfrac{1}{2}\times x\)发现递归下去了。
解这类方程其实需要运用极限的思想,但 是一种简单的解法是直接移项整理解出x=2 即可
这个期望dp最好的例子
附上我的证明
\(C_i=a_ib_i,a_i=i,b_i=\left( \dfrac{1}{2}\right)^i\),则:
(8)例题5-UVA10288
前置知识
概率为\(p\)的事件期望\(\dfrac{1}{p}\)次后发生
\(p\):在\(x\)次独立重复事件中,该事件发生\(xp\)次;
\(\dfrac{1}{p}\):该事件发生\(x\)次,所需独立重复事件发生\(\dfrac{x}{p}\)次。
题面
每张彩票上有一个漂亮图案,图案一共\(n\)种,如果你集齐了这\(n\)种图案就可以兑换大奖。
现在请问,在理想(平均)情况下,你买多少张彩票才能获得大奖的?
\(n\leq33\)
分析
设我们已经有了\(k\)个图案,则得到下一张新的牌的概率为\(\dfrac{n-k}{n}\).【前置知识】得到下一张牌的期望是\(\dfrac{n}{n-k}\)
定义\(E(i)\)表示\(i-1\)到第\(i\)张牌的期望,根据期望的线性性质可得:
模拟分数相加的过程,同分之后相加化简。
(9)例题6-高次期望-P1654
题面
一共有n次操作,每次操作只有成功与失败之分,成功对应1,失败对应0,n次操作对应为1个长度为n的01串。在这个串中连续的 \(X\) 个\(1\) 可以贡献 \(X^3\) 的分数,这\(X\)个1不能被其他连续的1所包含(也就是极长的一串1,具体见样例解释)
现在给出\(n\),以及每个操作的成功率,请你输出期望分数,输出四舍五入后保留1位小数。
样例
输入
3
0.5
0.5
0.5
输出
6.0
说明
000分数为0,001分数为1,010分数为1,100分数为1,101分数为2,110分数为8,011分数为8,111分数为27,总和为48,期望为48/8=6.0
\(N\leq 100000\)
题解
我们设\(E(X_{i})\)为在第 \(i\)个位置得的分数的期望
然后我们考虑 \(E(X_{i+1})\)和 \(E(X_{i})\)的关系
假设在\(i\)位置连续\(1\)串长度为 \(l\)的概率为 \(p_{l}\),在 \(i+1\)位置是 \(1\) 的概率为\(P\) ,那么对于每一个单独的 \(l\) 它都有\(P\)的概率对分数产生 \((3l^{2}+3l+1)\)的额外贡献
我们把所有可能的 \(l\) 一起考虑,就可以得到这个式子
然后我们可以发现
\(\sum_{l=0}^{i}p_{l}l^{2}=E(l^{2})\)
\(\sum_{l=0}^{i}p_{l}l=E(l)\)
于是我们将式子转化为
\(E(X_{i+1})=E(X_{i})+P\times(3E(l_{i}^{2})+3E(l_{i})+1)\)
然后我们就成功得出了分数的期望
同时我们也要维护\(E(l)\)和\(E(l^{2})\)
\(l\)和\(l^{2}\)都有 \(1\)~\(P\) 的概率变成0,\(P\)的概率增加
增加的量可以用上面类似的方法算出
由此我们就得出了全部的递推关系
其实三个量完全不用用数组存,只要改变一下转移顺序就行了
代码
#include <cstdio>
#include <algorithm>
using namespace std;
int n;
double ex,el,el2,P;
int main(){
scanf("%d",&n);
while(n--){
scanf("%lf",&P);
ex=ex+P*(3*el2+3*el+1);
el2=P*(el2+2*el+1);
el=P*(el+1);
}
printf("%.1f",ex);
return 0;
}
(10)例题7-P4450
题面
\(n\)个数\(1\)~\(n\),第\(k\)次取数需要\(k\)元,每次取数对于所有数概率均等(\(\dfrac{1}{n}\)),问取完\(n\)个数的期望花费
首先第一步很好转化吧,设用了\(x\)步,则花费为
现在就转换成要求上式的期望。
有了前面那题的基础现在考虑起来就简单了
维护一个线性期望\(a\),平方期望 \(f\)(都是数组)
\(a[i]\)表示找完\(i\)个数之后还需要的次数的期望
\(f[i]\)表示找完\(i\)个数之后还需要的次数平方的期望
不难想到最后的答案是 \(\dfrac{a[0]+f[0]}{2}\)
下面就开始考虑状态转移(dp?)
先来考虑 \(a[i]\)
情况1,买到买过的
买过的是i个,概率为 \(\dfrac{i}{n}\),花费就相当于记在买到i时候的账上了(从\(i\)账上查),得到花费为 \(a[i]+1\)
可得到式子\(\dfrac{i}{n}(a[i]+1)\)
情况2,买到没买过的
没买过的是\(n−i\)个,概率为 \(\dfrac{n-i}{n}\),花费就相当于记在买到\(i+1\)时候的
账上了(从\(i+1\)账上查),因为当前多买了一个,得到花费为 \(a[i+1]+1\)
可得到式子 \(\dfrac{n-i}{n}(a[i+1]+1)\)
两种情况一合并,得:
\(a[i]=\dfrac{i}{n}(a[i]+1)+\dfrac{n-i}{n}(a[i+1]+1)\)
这时就发现了,推着推着出现了\(i+1\),自然而然的想到了倒推
边界 \(a[n]=0\)都得全了还买什么
但是这个式子固然能做,是不是麻烦了点?
那么把它化简后发现:
\(a[i]=a[i+1]+\dfrac{n}{n-i}\)
然后考虑\(f[i]\)
跟推a的时候一个思路,新的或旧的,唯一就把平方拆开就行喽
\(f[i]=\dfrac{i}{n}(f[i]+2\times a[i]+1)+\dfrac{n-i}{n}(f[i+1]+2\times a[i+1]+1)\)
倒推
边界 \(f[n]=0\)
可算,但麻烦
化简
OK既然上面讲了写式子下面就说说化简的事吧~
把第一个括号拆成 \(f[i]\)和 \(2\times a[i]+1\)两部分
然后把
给移到左边,合并得:
然后两边同除 \(\dfrac{n-i}{n}\)
就简单一些了。
代码中精度转换注意一下,不要丢失
代码
#include<cstdio>
using namespace std;
double a[10005],f[10005];
int main()
{
int n;
scanf("%d",&n);
a[n]=0;
f[n]=0;
for(int i=n-1;i>=0;i--)
{
a[i]=a[i+1]+1.0*n/(n-i);
f[i]=1.0*i/(n-i)*(2*a[i]+1)+f[i+1]+2*a[i+1]+1;
}
printf("%.2lf\n",(f[0]+a[0])/2);
return 0;
}
(1)条件期望
【考察概率较低,感性理解】
假设你不断扔一个等概率的六面骰子,直到扔出6停止。求在骰子只出现过偶数的条件下扔骰子次数的期望。
细细的考虑一下,题目所说的并不是指出现奇数就pass再扔,而是出现奇数就终止了操作!!!
所以把条件这样转换后,就可以得到正确答案: \(\dfrac{3}{2}\)了
那我把题意转换一下:
假设你不断扔一个等概率的六面骰子,直到扔出\(1,3,5,6\)停止。求骰子最后一次是6的次数的期望。



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 开发中对象命名的一点思考
· .NET Core内存结构体系(Windows环境)底层原理浅谈
· C# 深度学习:对抗生成网络(GAN)训练头像生成模型
· .NET 适配 HarmonyOS 进展
· .NET 进程 stackoverflow异常后,还可以接收 TCP 连接请求吗?
· 本地部署 DeepSeek:小白也能轻松搞定!
· 基于DeepSeek R1 满血版大模型的个人知识库,回答都源自对你专属文件的深度学习。
· 在缓慢中沉淀,在挑战中重生!2024个人总结!
· 大人,时代变了! 赶快把自有业务的本地AI“模型”训练起来!
· Tinyfox 简易教程-1:Hello World!