Note - 树状数组

upd：翻云剪贴板的时候找到了神秘的柿子，更新了二维树状数组。

Intro

给出一个长度为 \(n\) 的一维数组 \(a\)，要求实现单点修改和区间查询。

如果我们直接使用暴力 for 循环依次求和，单点修改时间复杂度 \(O(1)\)，区间查询时间复杂度 \(O(n)\)。

考虑使用前缀和优化。设 \(pre_j = \sum_{i = 1} ^ j a_i\)，可以 \(O(n)\) 预处理得到。如果要求 \(a\) 数组区间 \([l, r]\) 的和，相当于求 \(\sum_{i = l} ^ r a_i = \sum_{i = 1} ^ r a_i - \sum_{i = l} ^ {l - 1} a_i = pre_r - pre_{l - 1}\)，这样我们就实现了 \(O(1)\) 的区间查询，但是单点修改时（假设修改 \(a_i\)），那么 \(pre_{i \sim n}\) 都需要重新计算，时间复杂度仍是 \(O(n)\)。

这时，我们就需要引入树状数组。

我用引入引入了树状数组？

How it works

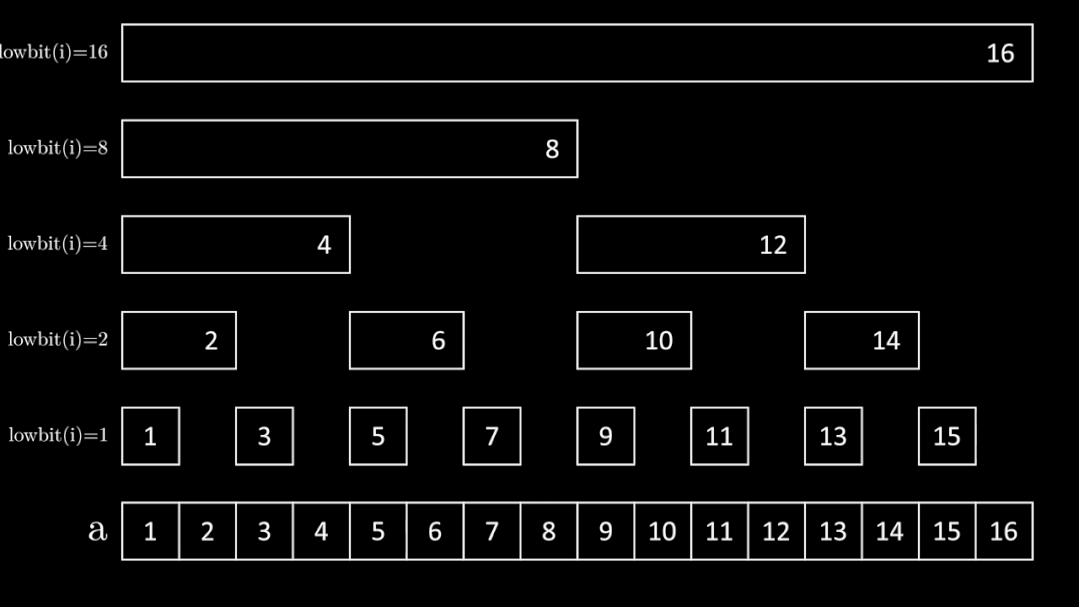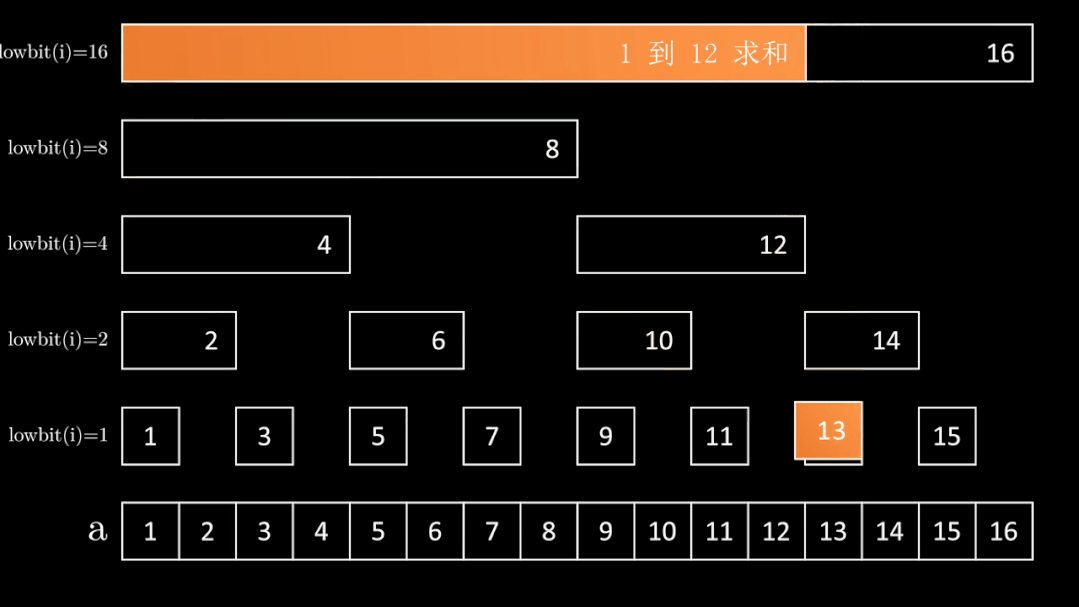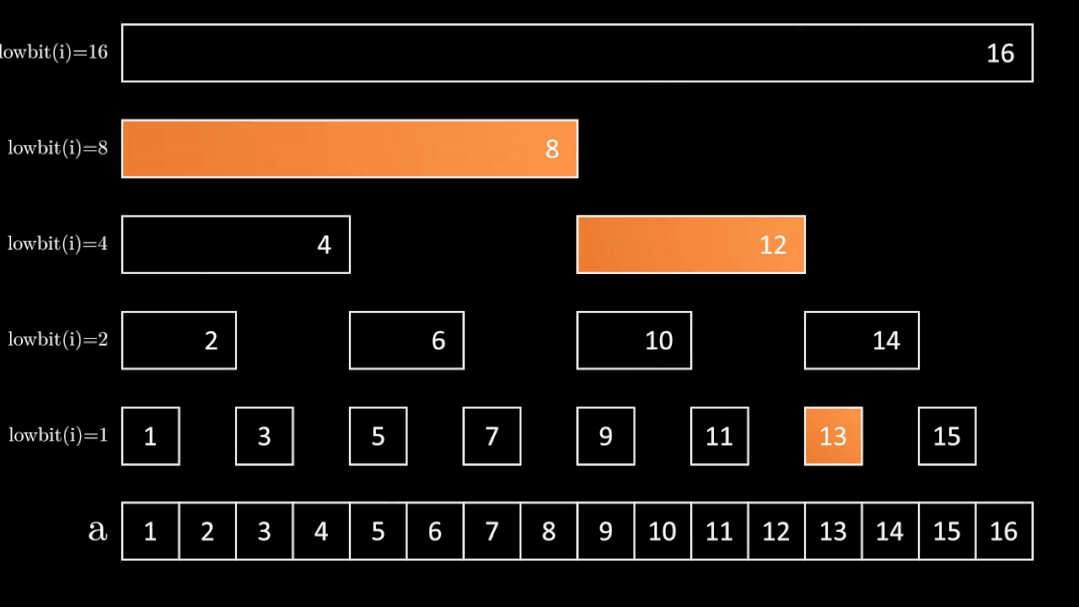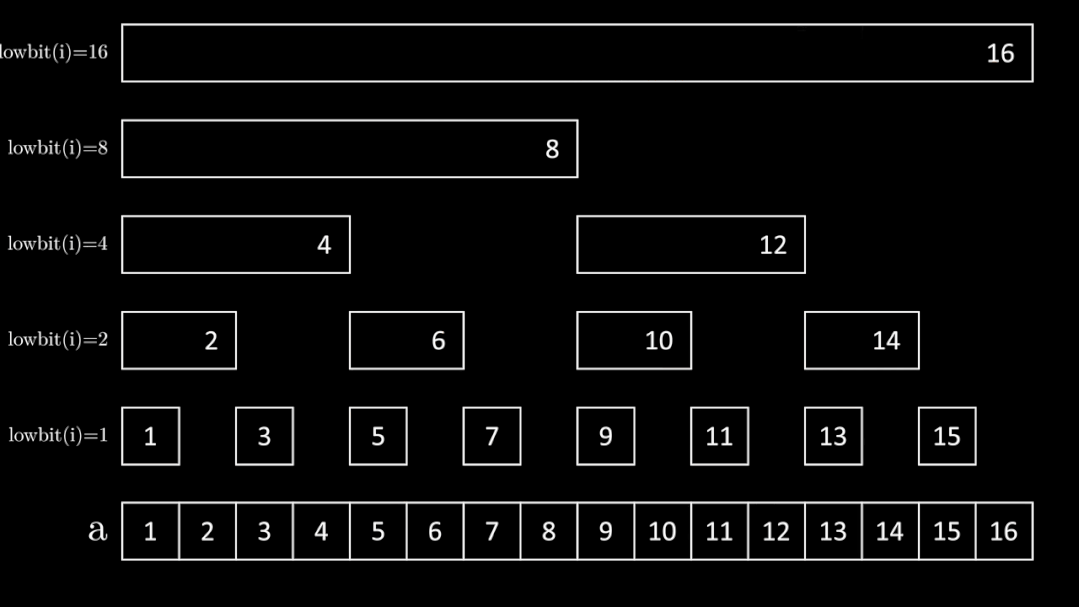
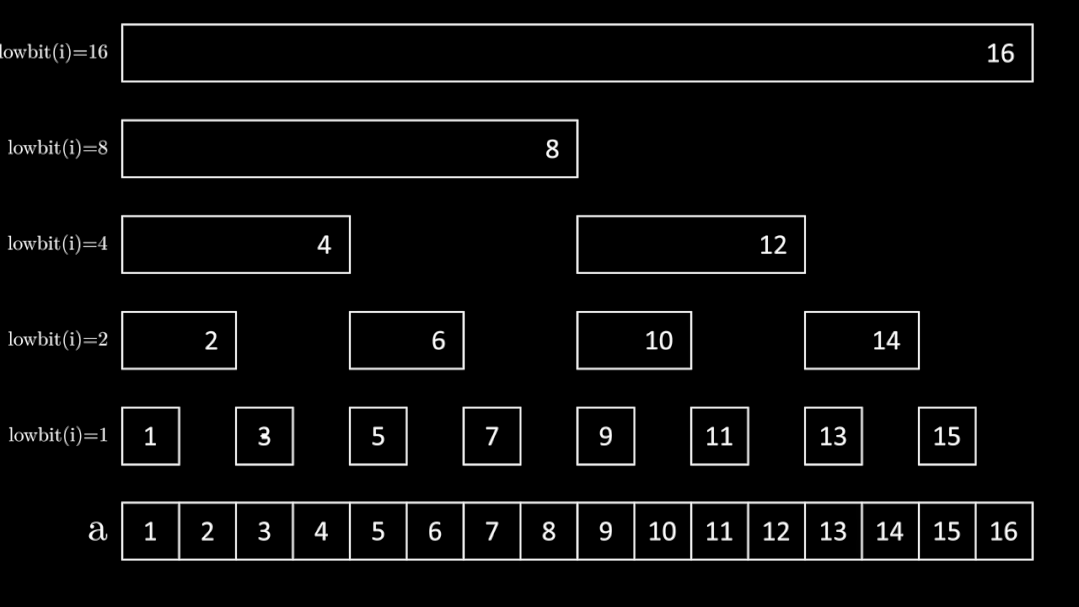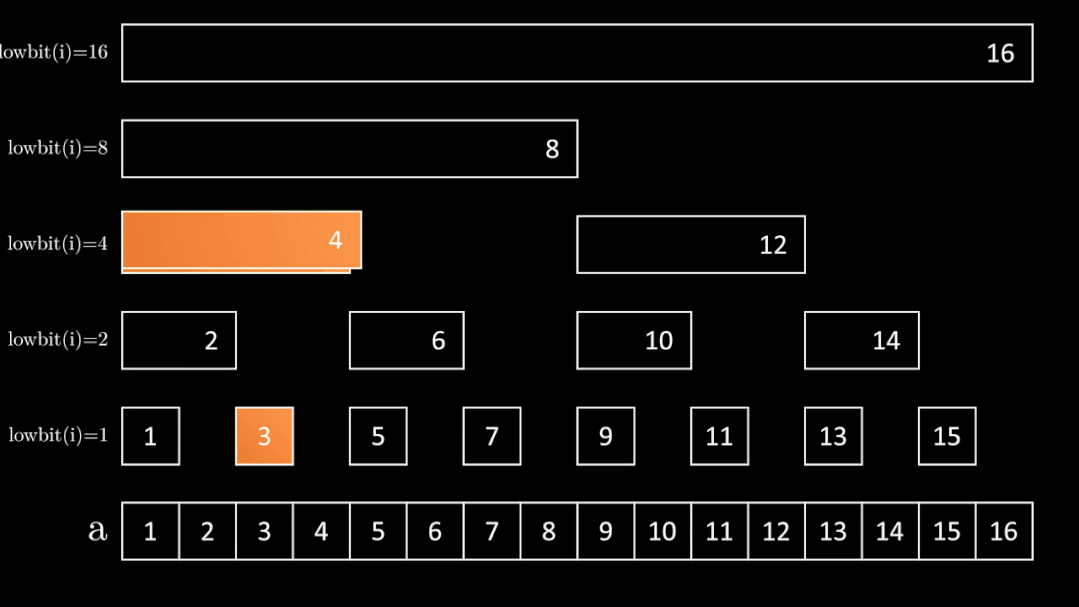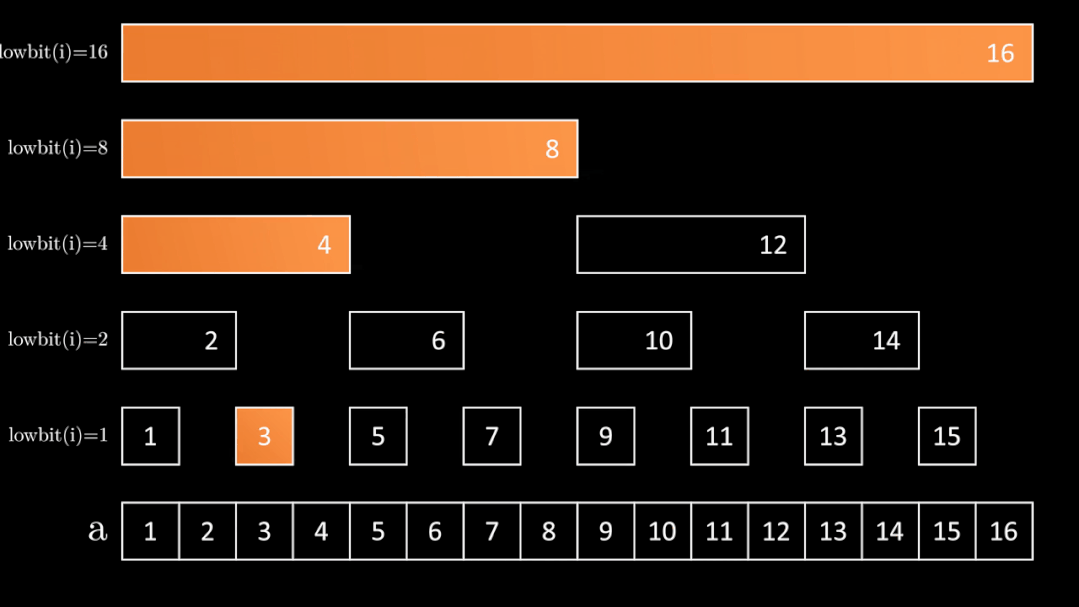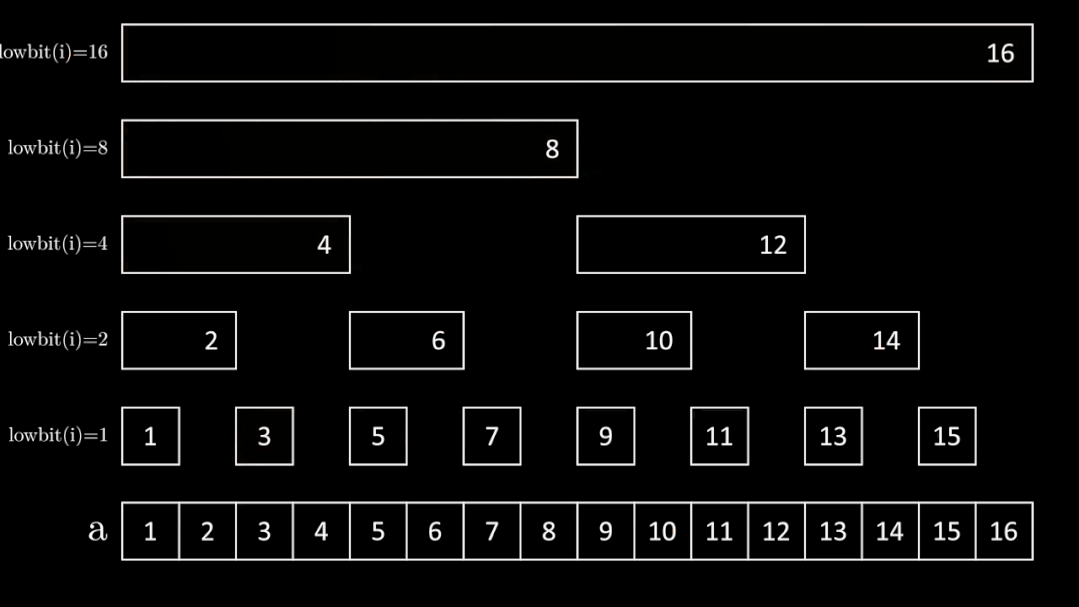
下面这张图展示了树状数组的工作原理：

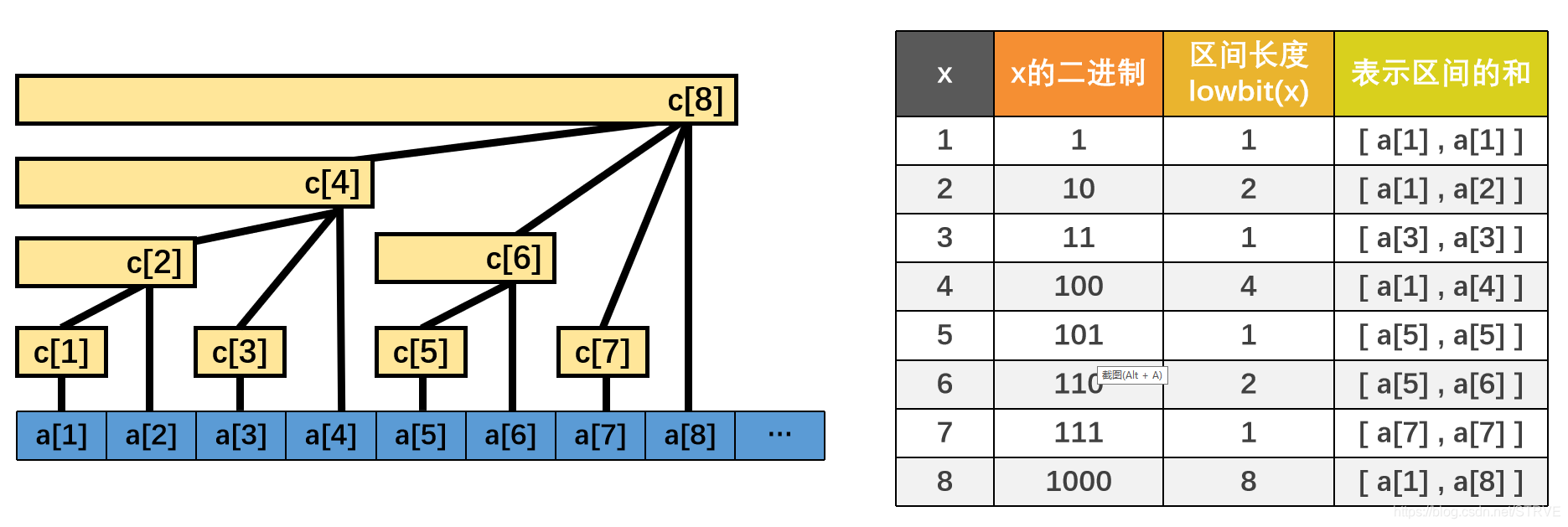
树状数组使用一个数组 \(c\) 来维护序列 \(a\) 的区间和（然后通过区间和来维护数组 \(a\) 的前缀和）。观察右图可以发现，\(c_i\) 存储的是序列 \(a\) 中区间为 \([i - \operatorname{lowbit}(i) + 1, i]\) 的元素之和，即 \(\sum_{j = i - \operatorname{lowbit}(i) + 1} ^ i a_i\)。

lowbit 是啥？能吃吗？

\(\operatorname{lowbit}(x)\) 表示 \(x\) 的二进制表示中，只保留最低位的 \(1\) 及其后面的 \(0\)，截断前面的内容，然后再转成十进制数的值。

例如 \(6 = (110)_2\)，保留最低位的 \(1\) 及其后面的 \(0\) 就是 \((10)_2 = 2\)，所以 \(c_6\) 就表示的是 \([6 - 2 + 1, 6]\) 即 \([5, 6]\) 这个区间。

How to calculate lowbit(x)？

假设原数为 \(x\)，那么把 \(x\) 转化为二进制后与 \(-x\) 的二进制按位与的结果就是 \(\operatorname{lowbit}(x)\)，用 C++ 表示就是 x & -x 或者 x & (~x + 1)（在 \(x\) 有符号时，~x + 1 等于 -x 的值）。

举个栗子，\(22\) 在计算机中的二进制为 \(010110\)，而 \(-22\) 在计算机中的二进制原码为 \(101001\)（就是二进制下的 \(22\) 各位反过来），补码为原码加一，即 \(101010\)。将 \(010110\) 与上 \(101010\)，便得到了 \((000010)_2 = 2\)，所以 \(\operatorname{lowbit}(22) = 2\)。

So does it have anything to do with it?

我们可以把二进制下的 \(x\) 化成 \(......100...0\) 这样的形式（中间的省略号都是 \(0\)），而出现的 \(1\) 就是 \(x\) 中的最低位的 \(1\)（第一个省略号中是 \(0\) 是 \(1\) 对 \(\operatorname{lowbit}(x)\) 没有影响）。那么 \(-x\) 的原码为 \(......011...1\)（中间的省略号都是 \(1\)），补码加上 \(1\)，为 \(......100...0\)（（中间的省略号都是 \(0\)），与原来的按位与，第一个省略号中的数字全部都反了过来，所以与起来是 \(0\)，只有原本 \(x\) 中的最低位的 \(1\) 保留了下来，再最后转成十进制，perfect！

性质

好吧讲完 lowbit 又把这图搬过来了。

再仔细观察，我们还可以发现更多性质：

1. \(c_i\) 表示的区间长度为 \(\operatorname{lowbit}(i)\)；
2. 除树根外，每个节点 \(c_i\) 的父节点是 \(c_{i + \operatorname{lowbit}(i)}\)（举个例子，\(\operatorname{lowbit}(4) = 4\)，那么 \(c_4\) 的父节点就是 \(c_{4 +4}\) 即 \(c_{8}\)，由图可知是对的）；
3. 树的深度为 \(\log n\)（比如这里 \(n = 8\)，深度就为 \(\log_2^8 = 4\)）。

这些性质非常重要！

How can it solve the problems mentioned at the beginning of the post?（单点修改和区间查询）

运用上述性质，考虑如何求解序列 \(a\) 中前 \(i\) 个元素的和。

尝试把 \([1, i]\) 和 lowbit 扯上关系，发现首先我们可以拆成 \([i - \operatorname{lowbit}(i) + 1, i]\) 这个区间，那么下一个区间就应该是 \([i - \operatorname{lowbit}(i) - \operatorname{lowbit}(i - \operatorname{lowbit}(i)) + 1, i - \operatorname{lowbit}(i)]\)，以此类推，直到不能再分为止。

发现每次 \(i\) 都减少了 \(\operatorname{lowbit}(i)\)，于是可以用如下代码输出区间 \([1, i]\) 分成的 \(\log i\) 个小区间：

int lowbit(int i) { return i & -i; }
while (i) {
	printf("[%d, %d]\n", i - lowbit(i) + 1, i);
	i -= lowbit(i);
}

这样把 \([1, i]\) 的区间拆分后，发现每个区间 \([i - \operatorname{lowbit}(i) + 1, i]\) 的和又等于 \(c_i\)，这样我们就可以以 \(O(\log n)\) 的时间复杂度来完成区间查询（因为树的深度为 \(\log n\)）。

代码如下：

int ask(int x) {
	int sum = 0;
	for (; x; x -= x & -x) sum += c[x];
	return sum;
}

现在我们解决了区间查询，如何解决单点修改呢？假如单点修改需要 \(O(n)\) 那还不如暴力呢。

其实，我们同样可以以 \(O(\log n)\) 的时间复杂度完成。

为什么又搬过来了啊喂。

假设我们在 \(a_3\) 增加了 \(k\)，现在我们如何正确维护序列的前缀和呢？观察可以发现，包含了区间 \([3, 3]\) 的区间只有 \(c_3\) 本身，以及 \(c_3\) 的父节点 \(c_4\)（\([1, 4]\)），\(c_4\) 的父节点 \(c_8\)（\([1, 8]\)）。

所以我们又可以得到：只有节点 \(c_i\) 和它所有的祖先节点保存的区间和包含了 \(a_i\)，因为每个 \(c_i\) 的父节点都是 \(c_{i + \operatorname{lowbit}(i)}\)，所以我们可以直接 i += lowbit(i) 循环，逐一更新 \(c_i\) 的值。因为树的深度为 \(\log n\)，所以这样做的复杂度也是 \(O(\log n)\) 的。

代码如下：

void add(int x, int k) {
	for (; x <= n; x += x & -x) c[x] += k;
}

所以最后，我们就以 \(O(\log n)\) 的时间复杂度实现了单点修改和区间查询。

「例题」单点修改，区间查询

原题目链接：Link。良心模板题。

直接使用上述的方法，注意这里 \(a\) 有初始序列，我们可以直接先把 \(c\) 初始化为 \(0\)，然后每次执行 add(i, a[i]) 即可。代码如下：

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e6 + 5;

int n, q, a[N], c[N];

void add(int k, int x) {
	for (int i = k; i <= n; i += i & -i)
		c[i] += x;
}

int ask(int x) {
	int sum = 0;
	for (int i = x; i; i -= i & -i)
		sum += c[i];
	return sum;
}
signed main() {
	scanf("%lld %lld", &n, &q);
	for (int i = 1; i <= n; i++)
		scanf("%lld", a + i), add(i, a[i]);
	while (q--) {
		int op, x, y;
		scanf("%lld %lld %lld", &op, &x, &y);
		if (op == 1) add(x, y);
		else printf("%lld\n", ask(y) - ask(x - 1)); // 区间和转化为前缀和相减
	}
	return 0;
}

区间修改和单点查询

接着我们要实现区间修改和单点查询。发现树状数组擅长维护前缀和，但此处区间需要的是修改而不是查询。

于是考虑差分。我们构造原数组的差分数组，用树状数组维护差分数组的前缀和，这样最后查询得到的就是原数组中的值。那么，将 \(a_l, a_{l + 1}, \cdots, a_r\) 都加上 \(k\)，我们就可以转换成在 \(a_l\) 加上 \(k\)，在 \(a_{r + 1}\) 加上 \(-k\)，这样求前缀和的时候就会抵消。通过差分，我们就把区间修改和单点查询转换成了树状数组擅长的单点修改和区间查询，very good！

「例题」树状数组 2 ：区间修改，单点查询

原题目链接：Link。还是模板。

实现细节见上。注意我们要维护差分数组，所以就不应该 add(i, a[i])，而是 add(i, a[i] - a[i - 1])。代码如下：

#include <bits/stdc++.h>
using namespace std;
#define int long long // I'm sorry but
const int N = 1e6 + 5;

int n, q, a[N], c[N], last;

void add(int k, int x) {
	for (int i = k; i <= n; i += i & -i)
		c[i] += x;
}

int ask(int x) {
	int sum = 0;
	for (int i = x; i; i -= i & -i)
		sum += c[i];
	return sum;
}
signed main() {
	scanf("%lld %lld", &n, &q);
	for (int i = 1; i <= n; i++)
		scanf("%lld", a + i), add(i, a[i] - last), last = a[i]; // 用一个 last 记录上一个元素的值
	while (q--) {
		int op, l, r, x;
		scanf("%lld", &op);
		if (op == 1) {
			scanf("%lld %lld %lld", &l, &r, &x);
			add(l, x);
			add(r + 1, -x);
		}
		else {
			scanf("%lld", &x);
			printf("%lld\n", ask(x));
		}
	}
	return 0;
}

区间修改和区间查询

我不会，长大后再学吧！~

其实和单点查询类似，首先通过差分实现区间修改。设差分数组为 \(b\)，然后写出区间查询 \([1, x]\) 查了个什么玩意（查前缀和，区间和可以相减得到）：

\[\sum_{i = 1} ^ x \sum_{j = 1} ^ i b_j \]

分析每个 \(b_j\) 被算的次数，可以得到 \(b_1\) 被算了 \(x\) 次，\(b_2\) 被算了 \(x - 1\) 次，一直到 \(b_x\) 被算了 \(1\) 次……于是上面的柿子可以变成：

\[\sum_{i = 1} ^ x (x - i + 1) \times b_i = \sum_{i = 1} ^ x (x + 1) \times b_i - \sum_{i = 1} ^ x i \times b_i = (x + 1) \sum_{i = 1} ^ x \times b_i - \sum_{i = 1} ^ x i \times b_i \]

观察我们最后得到的两个前缀和的柿子，发现我们只需要分别用两个树状数组维护 \(b_i\) 的前缀和与 \(b_i \times i\) 的前缀和即可。

「例题」区间修改，区间查询

原题目链接：Link。

模板，代码如下：

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e6 + 5;

int n, q, a[N], c[N], d[N];

void update(int k, int x) {
	for (int i = k; i <= n; i += i & -i)
		c[i] += x;
}

int ask(int x) {
	int sum = 0;
	for (int i = x; i; i -= i & -i)
		sum += c[i];
	return sum;
}

void add(int k, int x) {
	for (int i = k; i <= n; i += i & -i)
		d[i] += x;
}

int query(int x) {
	int sum = 0;
	for (int i = x; i; i -= i & -i)
		sum += d[i];
	return sum;
} // c 维护 b[i] 前缀和，d 维护 b[i] * i 前缀和
signed main() {
	scanf("%lld %lld", &n, &q);
	for (int i = 1; i <= n; i++)
		scanf("%lld", a[i]), update(i, a[i] - a[i - 1]), add(i, i * (a[i] - a[i - 1]));
	while (q--) {
		int op, l, r, x;
		scanf("%lld", &op);
		if (op == 1) {
			scanf("%lld %lld %lld", &l, &r, &x);
			update(l, x);
			update(r + 1, -x);
			add(l, l * x);
			add(r + 1, -(r + 1) * x);
		}
		else {
			scanf("%lld %lld", &l, &r);
			printf("%lld\n", (r + 1) * ask(r) - query(r) - (l * ask(l - 1) - query(l - 1)));
            // (r + 1) * ask(r) - query(r) 在查 [1, r]
            // (l + 1 - 1) * ask(l - 1) - query(l - 1) 在查 [1, l - 1]
            // 二者相减即是答案
		}
	}
	return 0;
} 

二维树状数组

区间修改区间查询。对于单点的自查二维前缀和那样维护。设 \(d\) 为差分数组，那么查询 \((1, 1)\) 到 \((x, y)\) 的区间和就是：

\[\sum_{i = 1} ^ x \sum_{j = 1} ^ y \sum_{k = 1} ^ i \sum_{l = 1} ^ j d_{k, l} = \sum_{i = 1} ^ x \sum_{j = 1} ^ y d_{i, j} \times (x + 1 - i) \times (y + 1 - j) = \sum_{i = 1} ^ x \sum_{j = 1} ^ y d_{i, j} \times ((x +1) \times (y + 1) - j \times (x +1) - i \times (y + 1) + i \times j) \]

用四个树状数组维护 \(d_{i, j}, d_{i, j} \times i, d_{i, j} \times j, d_{i, j} \times i \times j\)。

然后查某一区间就二维前缀和一下。下面是远古代码。

#include <bits/stdc++.h>
using namespace std;
const int N = 2048 + 1;

int n, m, op, a, b, c, d, x;
long long t1[N][N], t2[N][N], t3[N][N], t4[N][N], sum;

inline void update(register int x, register int y, register int v) {
	for (register int i = x; i <= n; i += i & -i)
		for (register int j = y; j <= m; j += j & -j)
			t1[i][j] += v, t2[i][j] += x * v, t3[i][j] += y * v, t4[i][j] += x * y * v;
}

inline long long ask(register int x, register int y) {
	sum = 0;
	for (register int i = x; i; i -= i & -i)
		for (register int j = y; j; j -= j & -j)
			sum += (x + 1) * (y + 1) * t1[i][j] - (y + 1) * t2[i][j] - (x + 1) * t3[i][j] + t4[i][j];
	return sum;
}
int main() {
	scanf("%d %d", &n, &m);
	while (~scanf("%d", &op)) {
		if (op == 1) {
			scanf("%d %d %d %d %d", &a, &b, &c, &d, &x);
			update(a, b, x);
			update(a, d + 1, -x);
			update(c + 1, b, -x);
			update(c + 1, d + 1, x);
		}
		else {
			scanf("%d %d %d %d", &a, &b, &c, &d);
			printf("%lld\n", ask(c, d) - ask(c, b - 1) - ask(a - 1, d) + ask(a - 1, b - 1));
		}
	}
	return 0;
}

树状数组求逆序对

求逆序对除了归并排序的 \(O(n \log n)\)，也有使用树状数组的 \(O(n \log K)\)，其中 \(K\) 是值域大小。

因为逆序对的本质就是每个元素前面的大于这个元素的值的元素个数之和（仔细理解这句话），所以我们可以根据元素的值建立一个树状数组，从 \(1 \sim n\) 循环每个元素 \(i\)，在树状数组中 \(a_i\) 的下标的值加一，代表是等于 \(a_i\) 的元素多了一个，然后通过前缀和求出不大于 \(a_i\) 的元素个数 \(num\)，用 \(i\) 减去 \(num\) 就是第 \(i\) 个元素前面值大于 \(a_i\) 的元素个数，累加到答案中即可。

后缀树状数组

交换 ask 和 add 的循环即可。可以感性理解，如：

void ask(int x, int k) {
	for (; x; x -= x & -x) bit[x] += k;
}

int ask(int x) {
	int sum = 0;
	for (; x <= n; x +=x & -x) sum += bit[x];
	return sum;
}

树状数组二分

很好用的一个 trick。直接二分一般就是 \(O(\log ^ 2 n)\)。但是可以用神秘方法优化到 \(O(\log n)\)。

怎么优化呢？原因在于我们进行了很多多余的 ask 操作。根据定义，或者根据代码：

int ask(int x) {
	int sum = 0;
	for (; x; x -= x & -x) sum += bit[x];
	return sum;
}

我们可以发现，如果查询的是 \(2 ^ i\)，那么就是完全 \(O(1)\) 的，直接就是 \(bit_{2 ^ i}\) 的值。利用这个，我们再加上倍增的思想，类似考虑 \(2\) 的次幂就可以了。和公路旅行非常像。

如查询树状数组中 \(\leq k\) 的最后一个位置，\(O(\log ^ 2 n)\)：

int ask(int x) {
	int sum = 0;
	for (; x; x -= x & -x) sum += bit[x];
	return sum;
}

int get(int k) {
	int l = 1, r = n;
	while (l < r) {
		int mid = l + r + 1 >> 1;
		if (ask(mid) <= k) l = mid;
		else r = mid - 1;
	}
	return l;
}

类似 lca 跳，模拟减去 \(\operatorname{lowbit}\) 的过程即可。\(O(\log n)\)：

int get(int k) {
	int sum = 0, ans = 0;
	for (int i = 19; ~i; i--) {
		int nans = ans + (1 << i);
		if (nans <= n && sum + bit[nans] <= k)
			ans = nans, sum += bit[nans]; // 类似 lca 跳，如果满足条件（这里是 <= k）就加上
	}
	return ans;
}