Holes To Fill,又名绚丽死亡走马灯【数学小姐我是你的狗特供版】
Exgcd
souvenir
可以用来求解同余方程 \(ax + by = \gcd(a, b)\)。当然你可以把结果框在一些范围内啥的。
faire
递归式,求解 gcd 的时候顺便求了。设递归下去的 \(a' = b, b' = a \bmod b\),已经求出一组解 \(a'x_0 + b'y_0 = \gcd(a', b')\),则 \(a'x_0 + b'y_0 = \gcd(a, b)\)。代入有 \(bx_0 + (a \bmod b)y_0 = bx_0 + (a - \lfloor \dfrac{a}{b} \rfloor b)y_0 = \gcd(a, b)\)。打开括号,交换一下有 \(ay_0 + b(x_ 0 - \lfloor \dfrac{a}{b} \rfloor y_0)\)。然后就有解 \(x = y_0, y = x_0 - \lfloor \dfrac{a}{b} \rfloor y_0\)。边界 \(b = 0\) 时,有特解 \(x = 1, y = 0\)。
int exgcd(int a, int b, int &x, int &y) {
if (!b) {
x = 1, y = 0;
return a;
}
int g = exgcd(b, a % b, x, y);
int t = x;
x = y;
y = t - (a / b) * y;
return g;
}
quelque chose
对于 \(ax + by = c\),先解 \(ax + by = \gcd(a, b)\),得到 \(ax_0 + by_0 = c\)。如果 \(\gcd(a, b) \nmid c\) 则无解。然后需要改变答案,\(x_0, y_0\) 乘上 \(\dfrac{c}{\gcd(a, b)}\) 即可。然后框定范围,因为改变 \(x_0, y_0\) 后结果不变,那么设 \(x_0\) 增加量为 \(k_1\),\(y_0\) 减少量为 \(k_2\),则 \(ak_1 = bk_2\)。发现只要 \(k_1 = \dfrac{b}{\gcd(a, b)}k, k_2 =\dfrac{a}{\gcd(a, b)}k\) 即可。
也就是说,\(x = x_0 + \dfrac{b}{\gcd(a, b)}k, y = y_0 - \dfrac{a}{\gcd(a, b)}k, k \in \mathbb{Z}\)。下面是把 \(x\) 框到非负数中。
int g = exgcd(a, b, x, y);
if (c % g) {
// no solution
}
x *= a / g;
int t = b / g;
x = (x % t + t) % t;
ExCRT
souvenir
解同余方程组。因为 ExCRT 没比 CRT 难到哪里去且应用更广,直接上 ExCRT 就行。
模板:给定 \(2n\) 个正整数 \(a_1,a_2,\cdots ,a_n\) 和 \(m_1,m_2,\cdots ,m_n\),求一个最小的正整数 \(x\),满足 \(\forall i\in[1,n],x\equiv a_i\ (\bmod m_i\ )\),或者给出无解。
faire
重点思想:合并。
考虑合并两条方程 \(x \equiv a_1 \ ( \bmod m_1\ ), x \equiv a_2 \ ( \bmod m_2\ )\)。则 \(x = m_1k_1 + a_1 = m_2k_2 + a_2\),\(m_1k_1 - m_2k_2 = a_2 - a_1\)。Exgcd 可求出 \(k_1, k_2\),又知道 \(x\) 的差为 \(\operatorname{lcm}(m_1, m_2)\),这就是合并后的 \(m'\)。
然后随便代一个 \(x = m_1k_1 + a_1 = m_2k_2 + a_2\) 能算 \(a'\)。逐条合并即可。
int excrt() {
for (int i = 2; i <= n; i++) {
int g = exgcd(m[1], m[i], x, y);
int c = a[i] - a[1];
if (c % g) return -1;
x *= c / g;
int t = m[i] / g;
x = (x % t + t) % t;
int l = m[1] / __gcd(m[1], m[i]) * m[i];
a[1] = (m[1] * x + a[1]) % l;
m[1] = l;
}
return a[1];
}
quelque chose
注意可能需要开 __int128?
2-SAT
souvenir
一般就是每个变量为 \(0 / 1\)(互斥),给出很多个关于两个变量的约束然后求解啥的。下文设 \(x\) 表示 \(1\),\(x'\) 表示 \(0\)。比如 \(x \oplus y = 1\),则连边 \(x \to y'\),\(x' \to y\),\(y \to x'\),\(y' \to x\)(单向的)。\(x \to y'\) 意思是”如果选了 \(x\),为了使 \(x \oplus y = 1\),只能有 \(y'\)。
faire
可以暴力 DFS。时间复杂度 \(\mathcal O(n ^ 2)\)。
bool dfs(int u) { // 这份代码 u ^ 1 为反集
if (vis[u]) return true;
if (vis[u ^ 1]) return false;
vis[u] = true;
s.push(u);
for (const int &v : e[u])
if (!dfs(v))
return false;
return true;
}
for (int i = 0; i < 2 * n; i += 2)
if (!vis[i] && !vis[i + 1]) {
while (s.size()) s.pop();
if (!dfs(i)) {
while (s.size()) vis[s.top()] = false, s.pop();
if (!dfs(i + 1)) return cout << "NIE" << endl, 0;
}
}
for (int i = 0; i < 2 * n; i += 2)
if (vis[i + 1]) cout << i + 2 << endl;
else cout << i + 1 << endl; // 这个是当时编号,输出加了 1
也可以用 Tarjan 强连通分量缩点,根据所在强连通分量编号确定。时间复杂度 \(\mathcal O(n + m)\)。
void dfs(int u, int fa) {
dfn[u] = low[u] = ++cnt;
s.push(u);
for (const int &v : e[u]) {
// if (v == fa) continue;
if (!dfn[v]) {
dfs(v, u);
low[u] = min(low[u], low[v]);
}
else if (!scc_id[v]) low[u] = min(low[u], dfn[v]);
}
if (low[u] == dfn[u]) {
int t;
scc_cnt++;
do {
t = s.top(); s.pop();
scc_id[t] = scc_cnt;
} while (t != u);
}
}
for (int i = 1; i <= 2 * n; i++)
if (!dfn[i]) dfs(i, i);
for (int i = 1; i <= n; i++)
if (scc_id[i] == scc_id[i + n])
return cout << "IMPOSSIBLE" << endl, 0; // 在同一强连通分量中(可互相到达)则无解
cout << "POSSIBLE" << endl;
for (int i = 1; i <= n; i++)
cout << (scc_id[i] > scc_id[i + n]) << " ";
quelque chose
如果要确定字典序最小啥的,只能上 DFS。
关于 DFS 解的构造,看代码 \(vis\) 数组显然;关于 Tarjan 解的构造,如果 \(x\) 和 \(x'\) 在同一 SCC 中无解,否则设 \(scc\_id_i\) 表示 \(i\) 的 SCC 编号,选更小的就好。也就是说,如果 \(scc\_id_x < scc\_id_{x'}\) 就选 \(x\),否则选 \(x'\)。证明见 解的构造。
如果强制 \(x\) 为 \(0\),可以连边 \(x \to x'\),vice versa。感性理解就是”即使你选了 \(1\),也给我来到 \(0\)“。
一道题目中,不同的 \(x\) 和 \(x'\) 含义可能不同,但是只要每个 \(x\) 只有 \(x\) 和 \(x'\) 就能 2-SAT。如 游戏。
Kruskal 重构树
souvenir
很神奇的树。
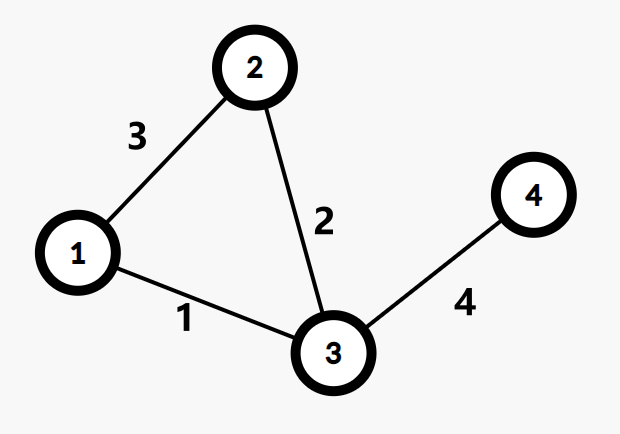
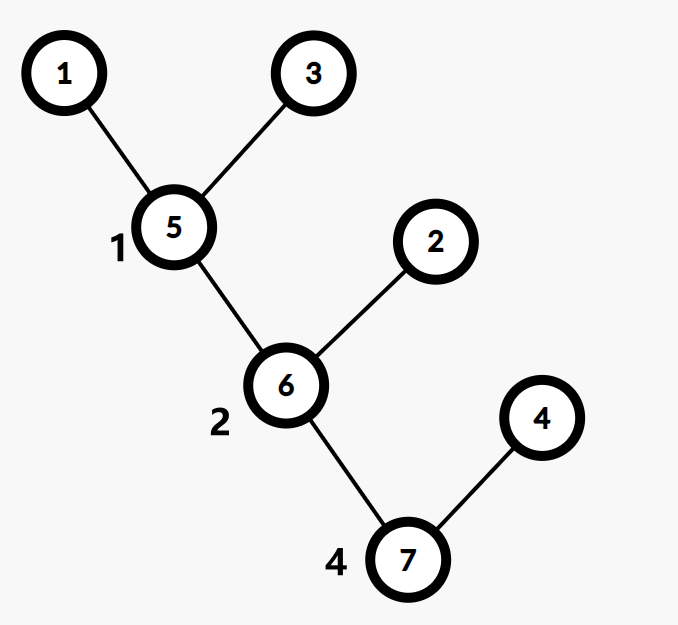
faire
在 Kruskal 跑生成树,合并两点的时候,新建一个点,并在点上维护信息(如两点之间边权),并以这两点作为儿子,就能建出 Kruskal 重构树。细节看代码。
时间复杂度就是 Kruskal 的。
void kruskal() {
for (int i = 1; i <= 2 * n - 1; i++) fa[i] = i, a[i] = 0, e2[i].clear();
sort(edge + 1, edge + 1 + m, [](node a, node b){ return a.a < b.a; });
tot = n;
for (int i = 1; i <= m; i++) {
int x = find(edge[i].u), y = find(edge[i].v);
if (x == y) continue;
a[++tot] = edge[i].a;
merge(x, tot);
merge(y, tot);
e2[tot].push_back(x);
e2[tot].push_back(y);
}
}
quelque chose
下面都是按照上图,边权从小到大建 Kruskal 重构树。
可以认为 Kruskal 重构树保存了每个历史版本的并查集连接信息,有点像可持久化并查集。
两点第一次连通时连通的边的边权,等于重构树上 LCA 的权值。
原图中两个点之间的所有简单路径上最大边权的最小值 ,等于最小生成树上两个点之间的简单路径上的最大值,等于 Kruskal 重构树上两点之间的 LCA 的权值。
由于树上建的点依次走下去,有单调性,可以倍增跳到最高的满足一些条件的点(如权值 \(\leq p\)),这个点的子树都满足 \(\leq p\),就转化为了区间操作。可以 DFS 序与神秘数据结构结合,如维护第 \(k\) 大: Peaks。可能的倍增写法:
for (int i = 18; ~i; i--)
if (f[v][i] && a[f[v][i]] <= x) v = f[v][i];
Tarjan 相关
souvenir
主要就是割点、割边(桥)、点双连通分量、边双连通分量、强连通分量。下面一堆 definition 来袭。
割点,就是删掉这个点后图不连通。
割边,就是删掉这条边后图不连通。
在一张连通的无向图中,对于两个点 \(u\) 和 \(v\),如果无论删去哪个点(只能删去一个,且不能删 \(u\) 和 \(v\)),\(u, v\) 都连通,则 \(u, v\) 点双连通。
在一张连通的无向图中,对于两个点 \(u\) 和 \(v\),如果无论删去哪条边(只能删去一条),\(u,v\) 都连通,则 \(u, v\) 边双连通。
强连通分量中,对于任意两个点 \(u, v\),\(u, v\) 都连通。
所以,,才发现不同的 \(low_u\) 定义是不一样的吗。。。wssb。
faire
割点如果不是根节点,设 \(v\) 是 \(u\) 的儿子,若 \(low_v \geq dfn_u\),即 \(v\) 不能走到 \(u\) 点“前面”的点,则 \(u\) 为割点;如果是根节点,看有多少子树,\(> 1\) 则为割点。
割边类似,如果 \(dfn_v > low_u\),即 \(v\) 不能走到 \(u\) 点本身,则 \((u, v)\) 就是一条割边。
Posted by liuzimingc

