欧拉积分
欧拉积分
两个公式:
$\Gamma(s)=\int_{0}^{+\infty}x^{s-1}e^{-x}dx,s>0$ (1)
$B(p,q)=\int_{0}^{1}x^{p-1}(1-x)^{q-1}dx,p>0,q>0$ (2)
一 、$\Gamma(Gamma)$函数
性质:
1.$\Gamma(s)$在定义域$s>0$内连续且可导.
2.递推公式$\Gamma(s+1)=s\Gamma(s)$ (3)
设$n<s\le{n+1},$即$0<s-n\le{1},$有递推公式(3)得到
$\Gamma(s+1)=s\Gamma(s)=s(s-1)\Gamma(s-1)=\cdots$
$=s(s-1)(s-2)\cdots(s-n)\Gamma(s-n).$
如果已知$Gamma(s)$在$0<s\le{1}$上的值,那么在其他范围内的函数值可由它计算出来
特别的有:$\Gamma(1)=\Gamma(2)=1$
$\Longrightarrow \Gamma(n+1)=n!\int_{0}^{\infty}e^{-x}dx=n!(n\in{N^{+}})$
3.$\Gamma$函数图像 及 函数定义域的延拓
$\Gamma(s)=\frac{\Gamma(s+1)}{s}$
当$-1<s<0$时,上式右端有意义,由右式可推出左边函数值,可依次延拓下去$\cdots\cdots$
图像如下:
![]()
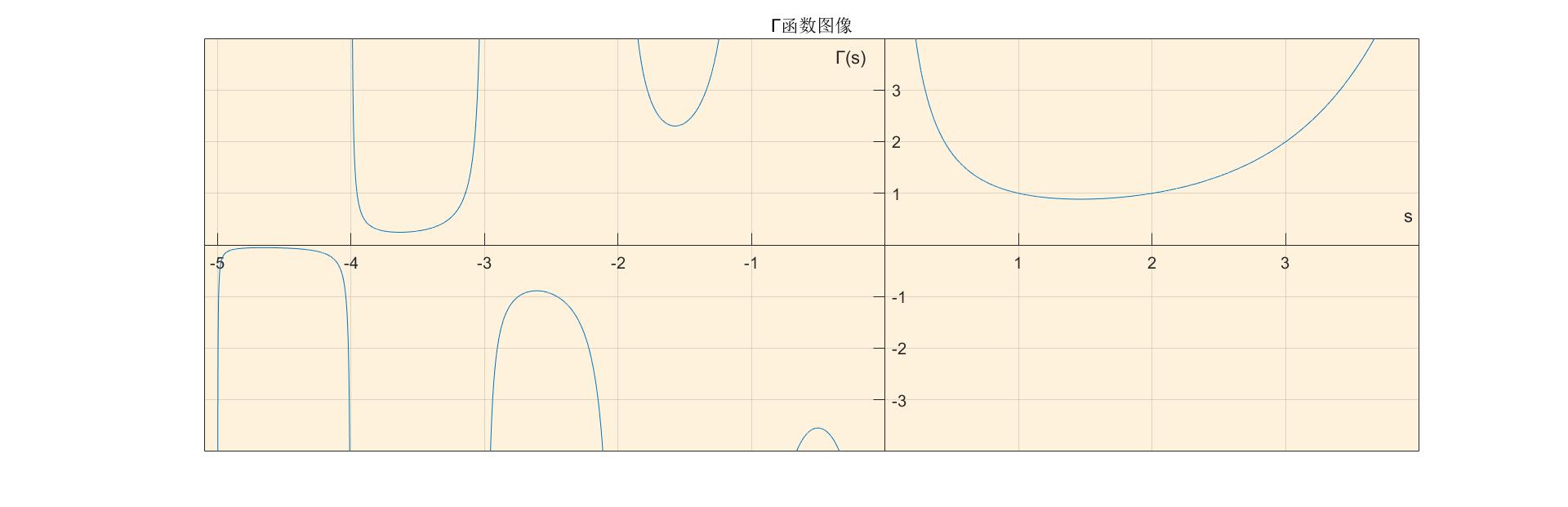
Matlab代码如下:
s = -5:0.0001:4;
plot(s,gamma(s)),xlabel('s'),ylabel('Γ(s)'),title('Γ函数图像');
axis([-5.1,4,-4,4]);
4.余元公式:
对$s\in(0,1),$有\[\Gamma(1-s)\Gamma(s)=\frac{\pi}{\sin{\pi x}}\]
由此推出重要概率公式 :\[\Gamma(\frac{1}{2})=\sqrt{\pi}\]
5.$\Gamma(s)$的其他形式
$\Gamma(s)=\int_{0}^{+\infty}x^{s-1}e^{-x}dx,s>0$
若令$x=y^2$,则
\[\Gamma(s)=2\int_{0}^{+\infty}y^{2s-1}e^{-y^2}dy,(s>0)\]
令$s=\frac{1}{2}$
$\Longrightarrow \int_{0}^{+\infty}e^{-y^2}dy=\Gamma(\frac{1}{2})=\frac{\sqrt{\pi}}{2}$
再令$2s-1=t,$或$s=\frac{1+t}{2},$即有
\[\int_{0}^{+\infty}e^{-y^{2}}u^{t}dy=\frac{1}{2}\Gamma(\frac{1+t}{2}) (t>-1)\]
令$x=py$,则
\[\Gamma(s)=p^{s}\int_{0}^{+\infty}y^{s-1}e^{-py}dy,(s>0,p>0)\]
$\Gamma$函数的应用:待续$\cdots\cdots$
1.$\Gamma$@广义阶乘:$Gamma$函数是阶乘函数在实数与复数上拓展的一类函数.
这实际上正与它的由来有关系。哥德巴赫在考虑数列插值问题时,成功把数列通项公式从整数延拓到实数集合。但无法解决阶乘往实数集上的延拓的问题,便写信请教伯努利兄弟,正好欧拉在一块,得知这个问题并最后成功解决该问题.
2.$\Gamma$@组合数学.
3.$\Gamma$@概率论.


【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步