深度学习综述

摘要： 深度学习可以完成需要高度抽象特征的人工智能任务，如语音识别、图像识别和检索、自然语言理解等。深层模型是包含多个隐藏层的人工神经网络，多层非线性结构使其具备强大的特征表达能力和对复杂任务建模能力。训练深层模型是长期以来的难题，近年来以层次化、逐层初始化为代表的一系列方法的提出给训练深层模型带来了希望，并在多个应用领域获得了成功。深层模型的并行化框架和训练加速方法是深度学习走向实用的重要基石，已有多个针对不同深度模型的开源实现，Google、Facebook、百度、腾讯等公司也实现了各自的并行化框架。深度学习是目前最接近人脑的智能学习方法，深度学习引爆的这场革命，将人工智能带上了一个新的台阶，将对一大批产品和服务产生深远影响。

深层模型的基本结构

深度学习采用的模型为深层神经网络（Deep Neural Networks，DNN）模型，即包含多个隐藏层（Hidden Layer，也称隐含层）的神经网络（Neural Networks，NN）。深度学习利用模型中的隐藏层，通过特征组合的方式，逐层将原始输入转化为浅层特征，中层特征，高层特征直至最终的任务目标。

深度学习源于人工神经网络的研究，先来回顾一下人工神经网络。一个神经元如下图所式[15]：

图1 神经元结构

这个神经元接受三个输入x1，x2，x3，神经元输出为

h(W,b) (x)=f(∑(i=1)^3▒〖W_i x_i+b〗)，

其中W1, W2, W3和b为神经元的参数，f(z)称为激活函数，一种典型的激活函数为Sigmoid函数，即f(z)=1/(1+e^(-z) )其图像为:

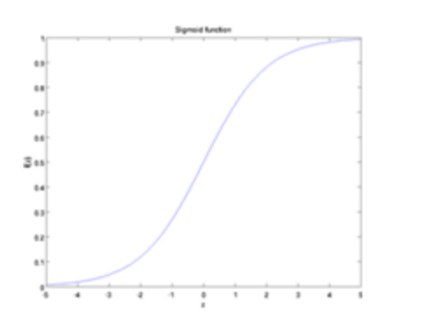
图2 Sigmoid函数图像

神经网络则是多个神经元组成的网络，一个简单的神经网络如下图所示:

图3 一个简单的神经网络

使用圆圈来表示神经网络的输入，标上“+1”的圆圈称为偏置节点，也就是截距项。神经网络最左边的一层叫做输入层（本例中，有3个输入单元，偏置单元不计）；最右的一层叫做输出层（本例中，输出层有2个节点）；中间的节点叫做隐藏层（本例中，有2个隐藏层，分别包含3个和2个神经元，偏置单元同样不计），因为不能在训练样本集中观测到它们的值。神经元网络中的每一条连线对应一个连接参数，连线个数对应网络的参数个数（本例共有４×３ ＋ ４×２ ＋３×２＝２６个参数）。求解这个的神经网络，需要（x(i)，y(i)）的样本集，其中x(i)是3维向量，y(i)是2维向量。

上图算是一个浅层的神经网络，下图是一个用于语音识别的深层神经网络。具有1个输入层，4个隐藏层和1个输出层，相邻两层的神经元全部连接。

图4 一种典型的深层神经网络模型

选择深层模型的原因

为什么要构造包含这么多隐藏层的深层网络结构呢？背后有一些理论依据：

天然层次化的特征

对于很多训练任务来说，特征具有天然的层次结构。以语音、图像、文本为例，层次结构大概如下表所示。

表1 几种任务领域的特征层次结构

以图像识别为例，图像的原始输入是像素，相邻像素组成线条，多个线条组成纹理，进一步形成图案，图案构成了物体的局部，直至整个物体的样子。不难发现，可以找到原始输入和浅层特征之间的联系，再通过中层特征，一步一步获得和高层特征的联系。想要从原始输入直接跨越到高层特征，无疑是困难的。

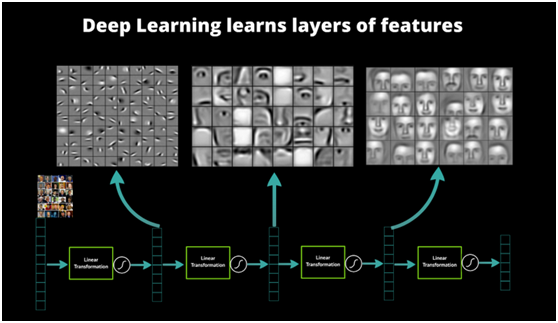
图5 人脸识别系统的多层结构和特征表示 [7]

特征的层次可表示性

特征的层次可表示性也得到了证实。1995年前后，Bruno Olshausen和David Field[8]收集了很多黑白风景照，从这些照片中找到了400个16×16的基本碎片，然后从照片中再找到其他一些同样大小的碎片，希望将其他碎片表示为这400个基本碎片的线性组合，并使误差尽可能小，使用的碎片尽可能少。表示完成后，再固定其他碎片，选择更合适的基本碎片组合优化近似结果。反复迭代后，得到了可以表示其他碎片的最佳的基本碎片组合。他们发现，这些基本碎片组合都是不同物体不同方向的边缘线。

图6 初级图像特征的提取和表示（Sparse Coding）（原图由Andrew Ng提供）

这说明可以通过有效的特征提取，将像素抽象成更高级的特征。类似的结果也适用于语音特征。

从浅层模型到深层模型

前文谈到了深层模型的结构和它的优势。事实上，深层模型具有强大的表达能力，并可以像人类一样有效提取高级特征，并不是新的发现。那么为什么深层模型直到最近几年才开始得到广泛的关注和应用呢？还是从传统的机器学习方法和浅层学习谈起。

浅层模型及训练方法

反向传播算法（Back Propagation，BP算法）[11]是一种神经网络的梯度计算方法。反向传播算法先定义模型在训练样本上的代价函数，再求代价函数对于每个参数的梯度。反向传播算法巧妙的利用了下层神经元的梯度可由上层神经元的残差导出的规律，求解的过程也正如算法的名字那样，自上而下反向逐层计算，直至获得所有参数的梯度。反向传播算法可以帮助训练基于统计的机器学习模型，从大量的训练样本中挖掘出统计规律，进而可对未标注的数据进行预测。这种基于统计的学习方法比起传统的基于规则的方法具备很多优越性[16]。

上世纪八九十年代，人们提出了一系列机器学习模型，应用最为广泛的包括支持向量机（Support Vector Machine，SVM）[12]和逻辑回归（Logistic Regression，LR）[13]，这两种模型分别可以看作包含1个隐藏层和没有隐藏层的浅层模型。训练时可以利用反向传播算法计算梯度，再用梯度下降方法在参数空间中寻找最优解。浅层模型往往具有凸代价函数，理论分析相对简单，训练方法也容易掌握，取得了很多成功的应用。

深层模型的训练难度

浅层模型的局限性在于有限参数和计算单元，对复杂函数的表示能力有限，针对复杂分类问题其泛化能力受到一定的制约。深层模型恰恰可以克服浅层模型的这一弱点，然而应用反向传播和梯度下降来训练深层模型，就面临几个突出的问题[10]：

1.梯局部最优。与浅层模型的代价函数不同，深层模型的每个神经元都是非线性变换，代价函数是高度非凸函数，采用梯度下降的方法容易陷入局部最优。

2.梯度弥散。使用反向传播算法传播梯度的时候，随着传播深度的增加，梯度的幅度会急剧减小，会导致浅层神经元的权重更新非常缓慢，不能有效学习。这样一来，深层模型也就变成了前几层相对固定，只能改变最后几层的浅层模型。

3.数据获取。深层模型的表达能力强大，模型的参数也相应增加。对于训练如此多参数的模型，小训练数据集是不能实现的，需要海量的有标记的数据，否则只能导致严重的过拟合（Over fitting）。

深层模型的训练方法

尽管挑战很大，Hinton教授并没有放弃努力，他30年来一直从事相关研究，终于有了突破性的进展。2006年，他在《Science》上发表了一篇文章[1]，掀起了深度学习在学术界和工业界的浪潮。这篇文章的两个主要观点是：

1.多隐藏层的人工神经网络具有优异的特征学习能力，学习到的特征对数据有更本质的刻画，从而有利于可视化或分类。

2.深度神经网络在训练上的难度，可以通过“逐层初始化”（Layer-wise Pre-training）来有效克服，文中给出了无监督的逐层初始化方法。

优异的特征刻画能力前文已经提到，不再累述，下面重点解释一下“逐层初始化”的方法。

图7 逐层初始化的方法（原图由Marc’Aurelio Ranzato提供）

给定原始输入后，先要训练模型的第一层，即图中左侧的黑色框。黑色框可以看作是一个编码器，将原始输入编码为第一层的初级特征，可以将编码器看作模型的一种“认知”。为了验证这些特征确实是输入的一种抽象表示，且没有丢失太多信息，需要引入一个对应的解码器，即图中左侧的灰色框，可以看作模型的“生成”。为了让认知和生成达成一致，就要求原始输入通过编码再解码，可以大致还原为原始输入。因此将原始输入与其编码再解码之后的误差定义为代价函数，同时训练编码器和解码器。训练收敛后，编码器就是我们要的第一层模型，而解码器则不再需要了。这时我们得到了原始数据的第一层抽象。固定第一层模型，原始输入就映射成第一层抽象，将其当作输入，如法炮制，可以继续训练出第二层模型，再根据前两层模型训练出第三层模型，以此类推，直至训练出最高层模型。

逐层初始化完成后，就可以用有标签的数据，采用反向传播算法对模型进行整体有监督的训练了。这一步可看作对多层模型整体的精细调整。由于深层模型具有很多局部最优解，模型初始化的位置将很大程度上决定最终模型的质量。“逐层初始化”的步骤就是让模型处于一个较为接近全局最优的位置，从而获得更好的效果。

浅层模型和深层模型的对比

表2 浅层模型和深层模型的对比

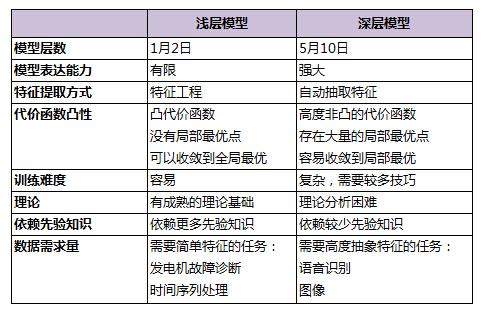
浅层模型有一个重要的特点，需要依靠人工经验来抽取样本的特征，模型的输入是这些已经选取好的特征，模型只用来负责分类和预测。在浅层模型中，最重要的往往不是模型的优劣，而是特征的选取的优劣。因此大多数人力都投入到特征的开发和筛选中来，不但需要对任务问题领域有深刻的理解，还要花费大量时间反复实验摸索，这也限制了浅层模型的效果。

事实上，逐层初始化深层模型也可以看作是特征学习的过程，通过隐藏层对原始输入的一步一步抽象表示，来学习原始输入的数据结构，找到更有用的特征，从而最终提高分类问题的准确性。在得到有效特征之后，模型整体训练也可以水到渠成。

深层模型的层次组件

深层模型是包含多个隐藏层的神经网络，每一层的具体结构又是怎样的呢？本节介绍一些常见的深层模型基本层次组件。

自编码器（Auto-Encoder）

一种常见的深层模型是由自编码器（Auto-Encoder）构造的[15]。自编码器可以利用一组无标签的训练数据{x(1), x(2), … }（其中x(i)是一个n维向量）进行无监督的模型训练。它采用反向传播算法，让目标值接近输入值。下图是一个自编码器的示例：

图8 自编码器

自编码器尝试训练一个恒等函数，让输出接近等于输入值，恒等函数看似没有学习的意义，但考虑到隐藏层神经元的数目（本例中为3个）小于输入向量的维数（本例中为6维），事实上隐藏层就变成了输入数据的一种压缩的表示，或说是抽象的简化表示。如果网络的输入是完全随机的，将高维向量压缩成低维向量会难以实现。但训练数据往往隐含着特定的结构，自编码器就会学到这些数据的相关性，从而得到有效的压缩表示。实际训练后，如果代价函数越小，就说明输入和输出越接近，也就说明这个编码器越靠谱。当然，自编码器训练完成后，实际使用时只需要它的前一层，即编码部分，解码部分就没用了。

稀疏自编码器（Sparse Auto-Encoder）是自编码器的一个变体，它在自编码器的基础上加入正则化（Regularity）。正则化是在代价函数中加入抑制项，希望隐藏层节点的平均激活值接近于0，有了正则化的约束，输入数据可以用少数隐藏节点表达。之所以采用稀疏自编码器，是因为稀疏的表达往往比稠密的表达更有效，人脑神经系统也是稀疏连接，每个神经元只与少数神经元连接。

降噪自编码器是另一种自编码器的变体。通过在训练数据中加入噪声，可训练出对输入信号更加鲁棒的表达，从而提升模型的泛化能力，可以更好地应对实际预测时夹杂在数据中的噪声。

得到自编码器后，我们还想进一步了解自编码器到底学到了什么。例如，在10×10的图像上训练一个稀疏自编码器，然后对于每个隐藏神经元，找到什么样的图像可以让隐藏神经元获得最大程度的激励，即这个隐藏神经元学习到了什么样的特征。将100个隐藏神经元的特征都找出来，得到了如下100幅图像：

图9 自编码器的隐藏神经元 [15]

可以看出，这100幅图像具备了从不同方向检测物体边缘的能力。显然，这样的能力对后续的图像识别很有帮助。

受限玻尔兹曼机（Restricted Boltzmann Machine，RBM）

受限玻尔兹曼机（Restricted Boltzmann Machine， RBM）是一个二部图，一层是输入层（v），另一层是隐藏层（h），假设所有节点都是随机二值变量节点，只能取值0或1，同时假设全概率分布p(v, h)满足Boltzmann分布。

图10受限玻尔兹曼机（RBM）

由于同层节点之间没有连接，因此已知输入层的情况下，隐藏层的各节点是条件独立的；反之，已知隐藏层的情况下，输入层各节点也是条件独立的。同时，可以根据Boltzmann分布，当输入v时通过p(h|v)生成隐藏层，得到隐藏层之后再通过p(v|h)生成输入层。相信很多读者已经猜到了，可以按照训练其他网络类似的思路，通过调整参数，希望通过输入v生成的h，再生成的v’与v尽可能接近，则说明隐藏层h是输入层v的另外一种表示。这样就可以作为深层模型的基本层次组件了。全部用RBM形成的深层模型为深度玻尔兹曼机（Deep Boltzmann Machine，DBM）。如果将靠近输入层的部分替换为贝叶斯信念网络，即有向图模型，而在远离输入层的部分仍然使用RBM，则称为深度信念网络（Deep Belief Networks，DBN）。

卷积神经网络（Convolutional Neural Networks, CNN）

以上介绍的编码器都是全连通网络，可以完成10×10的图像识别，如手写体数字识别问题。然而对于更大的图像，如100×100的图像，如果要学习100个特征，则需要1,000,000个参数，计算时间会大大增加。解决这种尺寸图像识别的有效方法是利用图像的局部性，构造一个部分联通的网络。一种最常见的网络是卷积神经网络（Convolutional Neural Networks，CNN）[19][20]，它利用图像固有的特性，即图像局部的统计特性与其他局部是一样的。因此从某个局部学习来的特征同样适用于另外的局部，对于这个图像上的所有位置，都能使用同样的特征。

具体地说，假设有一幅100×100的图像，要从中学习一个10×10的局部图像特征的神经元，如果采用全连接的方式，100×100维的输入到这个神经元需要有10000个连接权重参数。而采用卷积核的方式，只有10×10=100个参数权重，卷积核可以看作一个10×10的小窗口，在图像上上下左右移动，走遍图像中每个10×10的位置（共有91×91个位置）。每移动到一个位置，则将该位置的输入与卷积核对应位置的参数相乘再累加，得到一个输出值（输出值是91×91的图像）。卷积核的特点是连接数虽然很多，有91×91×10×10个连接，但是参数只有10×10=100个，参数数目大大减小，训练也变得容易了，并且不容易产生过拟合。当然，一个神经元只能提取一个特征，要提取多个特征就要多个卷积核。

下图揭示了对一幅8×8维图像使用卷积方法提取特征的示意过程。其中使用了3×3的卷积核，走遍图像中每个3×3的位置后，最终得到6×6维的输出图像：

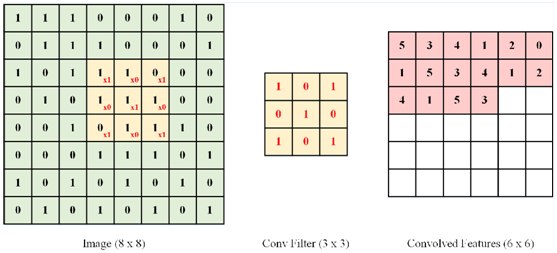
图11 8×8图像的卷积过程示意

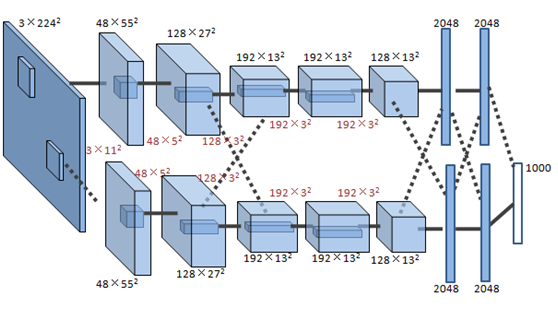
图12 用户图像分类的卷积神经网络

如图所示是Hinton的研究小组在ImageNet竞赛中使用的卷积神经网络[3]，共有5个卷积层，每层分别有96，256，384，384和256个卷积核，每层卷积核的大小分别为11×11，5×5，3×3，3×3和3×3。网络的最后两层是全连接层。

深度学习的训练加速

深层模型训练需要各种技巧，例如网络结构的选取，神经元个数的设定，权重参数的初始化，学习率的调整，Mini-batch的控制等等。即便对这些技巧十分精通，实践中也要多次训练，反复摸索尝试。此外，深层模型参数多，计算量大，训练数据的规模也更大，需要消耗很多计算资源。如果可以让训练加速，就可以在同样的时间内多尝试几个新主意，多调试几组参数，工作效率会明显提升，对于大规模的训练数据和模型来说，更可以将难以完成的任务变成可能。这一节就谈谈深层模型的训练加速方法。

GPU加速

矢量化编程是提高算法速度的一种有效方法。为了提升特定数值运算操作（如矩阵相乘、矩阵相加、矩阵-向量乘法等）的速度，数值计算和并行计算的研究人员已经努力了几十年。矢量化编程强调单一指令并行操作多条相似数据，形成单指令流多数据流（SIMD）的编程泛型。深层模型的算法，如BP，Auto-Encoder，CNN等，都可以写成矢量化的形式。然而，在单个CPU上执行时，矢量运算会被展开成循环的形式，本质上还是串行执行。

GPU（Graphic Process Units，图形处理器）的众核体系结构包含几千个流处理器，可将矢量运算并行化执行，大幅缩短计算时间。随着NVIDIA、AMD等公司不断推进其GPU的大规模并行架构支持，面向通用计算的GPU（General-Purposed GPU, GPGPU）已成为加速可并行应用程序的重要手段。得益于GPU众核（many-core）体系结构，程序在GPU系统上的运行速度相较于单核CPU往往提升几十倍乃至上千倍。目前GPU已经发展到了较为成熟的阶段，受益最大的是科学计算领域，典型的成功案例包括多体问题（N-Body Problem）、蛋白质分子建模、医学成像分析、金融计算、密码计算等。

利用GPU来训练深度神经网络，可以充分发挥其数以千计计算核心的高效并行计算能力，在使用海量训练数据的场景下，所耗费的时间大幅缩短，占用的服务器也更少。如果对针对适当的深度神经网络进行合理优化，一块GPU卡可相当于数十甚至上百台CPU服务器的计算能力，因此GPU已经成为业界在深度学习模型训练方面的首选解决方案。

数据并行

数据并行是指对训练数据做切分，同时采用多个模型实例，对多个分片的数据并行训练。

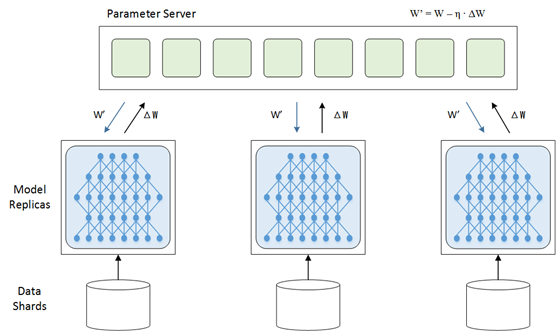
图13 数据并行的基本架构 [17]

要完成数据并行需要做参数交换，通常由一个参数服务器（Parameter Server）来帮助完成。在训练的过程中，多个训练过程相互独立，训练的结果，即模型的变化量ΔW需要汇报给参数服务器，由参数服务器负责更新为最新的模型W’ = W – η ∙ ΔW，然后再将最新的模型W’分发给训练程序，以便从新的起点开始训练。

数据并行有同步模式和异步模式之分。同步模式中，所有训练程序同时训练一个批次的训练数据，完成后经过同步，再同时交换参数。参数交换完成后所有的训练程序就有了共同的新模型作为起点，再训练下一个批次。而异步模式中，训练程序完成一个批次的训练数据，立即和参数服务器交换参数，不考虑其他训练程序的状态。异步模式中一个训练程序的最新结果不会立刻体现在其他训练程序中，直到他们进行下次参数交换。

参数服务器只是一个逻辑上的概念，不一定部署为独立的一台服务器。有时候它会附属在某一个训练程序上，有时也会将参数服务器按照模型划分为不同的分片，分别部署。

模型并行

模型并行将模型拆分成几个分片，由几个训练单元分别持有，共同协作完成训练。当一个神经元的输入来自另一个训练单元上的神经元的输出时，产生通信开销。

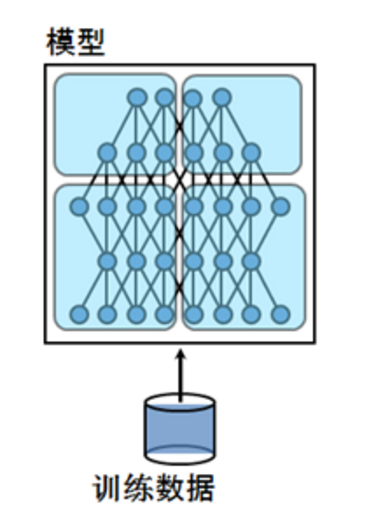
图14 模型并行的基本架构 [17]

多数情况下，模型并行带来的通信开销和同步消耗超过数据并行，因此加速比也不及数据并行。但对于单机内存无法容纳的大模型来说，模型并行是一个很好的选择。令人遗憾的是，数据并行和模型并行都不能无限扩展。数据并行的训练程序太多时，不得不减小学习率，以保证训练过程的平稳；模型并行的分片太多时，神经元输出值的交换量会急剧增加，效率大幅下降。因此，同时进行模型并行和数据并行也是一种常见的方案。如下图所示，4个GPU分为两组，GPU0，1为一组模型并行，GPU2，3为另一组，每组模型并行在计算过程中交换输出值和残差。两组GPU之间形成数据并行，Mini-batch结束后交换模型权重，考虑到模型的蓝色部分由GPU0和GPU2持有，而黄色部分由GPU1和GPU3持有，因此只有同色的GPU之间需要交换权重。

图15 4GPU卡的数据并行和模型并行混合架构

计算集群

搭建CPU集群用于深度神经网络模型训练也是业界常用的解决方案，其优势在于利用大规模分布式计算集群的强大计算能力，利用模型可分布式存储、参数可异步通信的特点，达到快速训练深层模型的目的。

CPU集群方案的基本架构包含用于执行训练任务的Worker、用于分布式存储分发模型的参数服务器（Parameter Server）和用于协调整体任务的主控程序（Master）。CPU集群方案适合训练GPU内存难以容纳的大模型，以及稀疏连接神经网络。Andrew Ng和Jeff Dean在Google用1000台CPU服务器，完成了模型并行和Downpour SGD数据并行的深度神经网络训练[17]。

结合GPU计算和集群计算技术，构建GPU集群正在成为加速大规模深度神经网络训练的有效解决方案。GPU集群搭建在CPU-GPU系统之上，采用万兆网卡或Infiniband等更加快速的网络通信设施，以及树形拓扑等逻辑网络拓扑结构。在发挥出单节点较高计算能力的基础上，再充分挖掘集群中多台服务器的协同计算能力，进一步加速大规模训练任务。

参考文献

[1] Geoffery E. Hinton, Salakhutdinov RR. Reducing the dimensionality of data with neural networks. Science. 2006 Jul 28;313(5786):504-7.

[2] Geoffrey E. Hinton, Simon Osindero, Yee-Whye Teh, A fast learning algorithm for deep belief nets Neural Compute, 18(7), 1527-54 (2006)

[3] ImageNet Classification with Deep Convolutional Neural Networks, Alex Krizhevsky, Ilya Sutskever, Geoffrey E Hinton, NIPS 2012.

[4] Q.V. Le, M.A. Ranzato, R. Monga, M. Devin, K. Chen, G.S. Corrado, J. Dean, A.Y. Ng. Building high-level features using large scale unsupervised learning. ICML, 2012.

[5] Rick Rashid, Speech Recognition Breakthrough for the Spoken, Translated Wordhttp://

[6] NYU “Deep Learning” Professor LeCun Will Lead Facebook’s New Artificial Intelligence Lab. 

[7] A Primer on Deep Learning

[8] Bruno A. Olshausen & David J. Field, Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature. Vol 381. 13 June, 1996

[9] Andrew Ng. Machine Learning and AI via Brain simulations,

[10] Deep Networks Overview

[11] Back propagation algorithm

[12] Support Vector Machine 

[13] Logistic Regression 

[14] The Nobel Prize in Physiology or Medicine 1981.

[15] Stanford deep learning tutorial

[16] 余凯，深度学习-机器学习的新浪潮，Technical News程序天下事

[17] Dean, J., Corrado, G.S., Monga, R., et al, Ng, A. Y. Large Scale Distributed Deep Networks. In Proceedings of the Neural Information Processing Systems (NIPS’12) (Lake Tahoe, Nevada, United States, December 3–6, 2012). Curran Associates, Inc, 57 Morehouse Lane, Red Hook, NY, 2013, 1223-1232.

[18] Geoffrey Hinton：UCLTutorial on: Deep Belief Nets

[19] Y. LeCun and Y. Bengio. Convolutional networks for images, speech, and time-series. In M. A. Arbib, editor, The Handbook of Brain Theory and Neural Networks. MIT Press, 1995

[20] Introduction to Convolutional neural network

[21] Krizhevsky, Alex. “ImageNet Classification with Deep Convolutional Neural Networks”. Retrieved 17 November 2013.

[22] Kaldi project 

[23] Povey, D., Ghoshal, A. Boulianne, G., et al, Vesely, K. Kaldi. The Kaldi Speech Recognition Toolkit. in Proceedings of IEEE 2011 Workshop on Automatic Speech Recognition and Understanding(ASRU 2011) (Hilton Waikoloa Village, Big Island, Hawaii, US, December 11-15, 2011). IEEE Signal Processing Society. IEEE Catalog No.: CFP11SRW-USB.

[24] cuda-convent 

[25] Krizhevsky, A., Sutskever, I., and Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the Neural Information Processing Systems (NIPS’12) (Lake Tahoe, Nevada, United States, December 3–6, 2012). Curran Associates, Inc, 57 Morehouse Lane, Red Hook, NY, 2013, 1097-1106.

[26] Krizhevsky, A. Parallelizing Convolutional Neural Networks. in tutorial of IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2014). (Columbus, Ohio, USA, June 23-28, 2014). 2014.

[27] caffe 

[28] Jia, Y. Q. Caffe: An Open Source Convolutional Architecture for Fast Feature Embedding.  (2013).

[29] Theano 

[30] J. Bergstra, O. Breuleux, F. Bastien, P. Lamblin, R. Pascanu, G. Desjardins, J. Turian, D. Warde-Farley and Y. Bengio. Theano: A CPU and GPU Math Expression Compiler. Proceedings of the Python for Scientific Computing Conference (SciPy) 2010. June 30 - July 3, Austin, TX.

[31] Overfeat 

[32] Torch7 http://torch.ch

[33] Coates, A., Huval, B., Wang, T., Wu, D. J., Ng, A. Y. Deep learning with COTS HPC systems. In Proceedings of the 30th International Conference on Machine Learning (ICML’13) (Atlanta, Georgia, USA, June 16–21, 2013). JMLR: W&CP volume 28(3), 2013, 1337-1345.

[34] Yadan, O., Adams, K., Taigman, Y., Ranzato, M. A. Multi-GPU Training of ConvNets. arXiv:1312.5853v4 [cs.LG] (February 2014)

[35] Kaiyu, Large-scale Deep Learning at Baidu, ACM International Conference on Information and Knowledge Management (CIKM 2013)

[36] aaronzou, Mariana深度学习在腾讯的平台化和应用实践

[37] “Convolutional Neural Networks (LeNet) - DeepLearning 0.1 documentation”. DeepLearning 0.1. LISA Lab. Retrieved 31 August 2013.

[38] Bengio, Learning Deep Architectures for AI，；

[39] Deep Learning 

[40] Deep Learning 

[41] Introduction to Deep Learning. 

[42] Google的猫脸识别:人工智能的新突破

[43] Andrew Ng’s talk video: 

[44] Invited talk “A Tutorial on Deep Learning” by Dr. Kai Yu

转自：深度学习（Deep Learning）系列篇（1）：深度学习在腾讯的平台化和应用实践（全）

posted @ 2017-08-07 09:32  liurio  阅读(1874)  评论(0)  编辑  收藏  举报