Python写基于非线性优化的2D-SLAM系统（已开源）

我的CSDN：https://blog.csdn.net/liu2015302026/article/details/107997270
Github代码地址:
https://github.com/liuzhenboo/2D-SLAM-By-Nonlinear-Optimization

1. SLAM问题概率模型

1.1 最大后验到最小二乘

SLAM问题其实就是一个状态估计的问题，就是要根据一系列观测来推测状态量；一般情况下，我们把SLAM问题建立在概率论的框架下。

说白了，SLAM就是要是解决这样一类后验概率问题：

\[ p(x|z) \]

其中\(x\)是系统当前状态量，\(z\)是与状态量相关的观测量；在求出这个条件概率之后，把观测值\(Z\)带入，就可以获得\(p(x|z=Z)\)，这也就是我们需要的分布。

根据概率公式展开：

\[p(x|z=Z)=\frac{p(z=Z|x)p(x)}{p(z=Z)} \]

其中分母是常量，当作是归一化因子\(\eta\)即可，所以也可写为：

\[p(x|z=Z)=\eta{p(z=Z|x)p(x)} \]

\(p(z|x)\)表示在\(x\)已知的情况下，\(z\)的概率分布；在求出\(p(z|x)\)之后，把\(z=Z\)带入，得到\(p(z=Z|x)\)，它也被称为似然项，它表示在\(x\)取不同值的情况下，\(z=Z\)的概率。

\(p(x)\)也被称为先验，也就是在观测之前\(x\)服从什么分布。这可以通过其他信息源得到，比如GPS，惯导等。如果事前不知道任何先验分布信息，那么可以将其设为1，表示不相信先验信息，只根据系统使用的量测来估计。

\[ x_{MAP}= \mathop{argmax}\limits_{x}p(z=Z|x)p(x) \]

因为每次观测相互独立，所以上式可以写为：

\[ x_{MAP}= \mathop{argmax}\limits_{x}\prod_{i}p(z_i=Z_i|x)p(x) \]

取负对数得到：

\[ x_{MAP}=\mathop{argmin}\limits_{x}\left[-\sum_ilogp(z_i=Z_i|x)-logp(x)\right] \]

如果假设观测\(p(z_i|x)\)服从高斯分布\(N(h_i(x)，\sum_i)\)；先验\(p(x)\)服从\(N(x_p，\sum_{x})\)那么有：

\[ x_{MAP}=\mathop{argmin}\limits_{x}\sum_{i}||z_i-h_i(x)||^2_{\sum_i}+||x-x_p||^2_{\sum_x} \]

如果没有先验知识，那么可以写为：

\[ x_{MAP}=\mathop{argmin}\limits_{x}\sum_{i}||z_i-h_i(x)||^2_{\sum_i} \]

显而易见，在SLAM的过程中，不断有新的残差项加入到系统，上述最小乘问题不断扩大。

1.2 非线性优化求解

设当前时刻状态向量为x，维度为n，我们将残差表示成向量的形式：

\[ e(x) = \left[\begin{matrix} e_1(x) \\ ... \\ e_m(x) \end{matrix}\right] \]

这里我们使用马氏范数，损失函数定义为：

\[ E(x) =\frac{1}{2}||e(x)||^2_{\Sigma_e}= \frac{1}{2}{e(x)}^T\Sigma_e^{-1}e(x) \]

记\(J_i(x)=\frac {\partial e_i(x)} {\partial x}\)，那么可以得到：

\[ \frac {\partial e(x)}{\partial x}= J = \left[\begin{matrix} J_1(x) \\ ... \\ J_m(x) \end{matrix}\right] \]

\[ J_i(x) =\left[\begin{matrix} \frac {\partial e_i(x)} {\partial x_1} ... \frac {\partial e_i(x)} {\partial x_n} \end{matrix}\right] \]

对残差函数泰勒展开，得到一阶近似：

\[ e(x+\delta x) \approx e(x)+J\delta x \]

那么带入损失函数可以近似得到：

\[ E(x+\delta x) = \frac{1}{2}{e(x+\delta x)}^T\Sigma_e^{-1}e(x+\delta x) \\ \approx \frac{1}{2}{e(x)}^T\Sigma _e^{-1}e(x)+{\delta x}^T J^T \Sigma_e^{-1}e(x)+\frac{1}{2}{\delta x}^TJ^T\Sigma_e^{-1}J\delta x \]

所以损失函数就转换为关于\(\delta x\)的二次函数，并且如果\(J^T\Sigma _e^{-1}J\)正定，那么损失函数有最小值。

对上式关于\(\delta x\)求一阶导数，并另其为零，得：

\[ J^T\Sigma_e^{-1}J\delta x = -J^T\Sigma_e^{-1}e(x) \]

也常常写为

\[ H\delta x = b \]

这样就可以得到增量\(\delta x\)，这样一直迭代，就可以不断优化当前解，直到误差小于阈值。这种方法被称为高斯牛顿法。

不过在实际中，求解上述方程需要\(H\)矩阵可逆，而我在编程中，经常遇到\(H\)不可逆的情况，所以实际代码中我使用了Levenberg-Marquardt法。其是对高斯牛顿法进行了改进，增加了阻尼因子一项，如下所示：

\[ (H+\mu I)\delta x = b \]

这里我并没有深究迭代中\(\mu\)的动态选取策略，只是单纯地给了一个定值0.1。

2. 问题设定

一个机器人佩戴某种雷达传感器在2D平面内运动，如何通过带有噪声的传感器数据来得到自身的定位？

假设：

（1）2D平面内有若干带有不同id号的路标点（landmark）

（2）传感器用于观测路标点的信息，观测范围是一个以自身位置为原点，r为半径的圆。其观测量有三个，第一个观测量是探测范围内路标点在传感器坐标系中的x值，满足正态分布；第二个观测量是探测范围内路标点在传感器坐标系中的y值，满足正态分布；第三个观测为路标点的id号。

如下图所示：

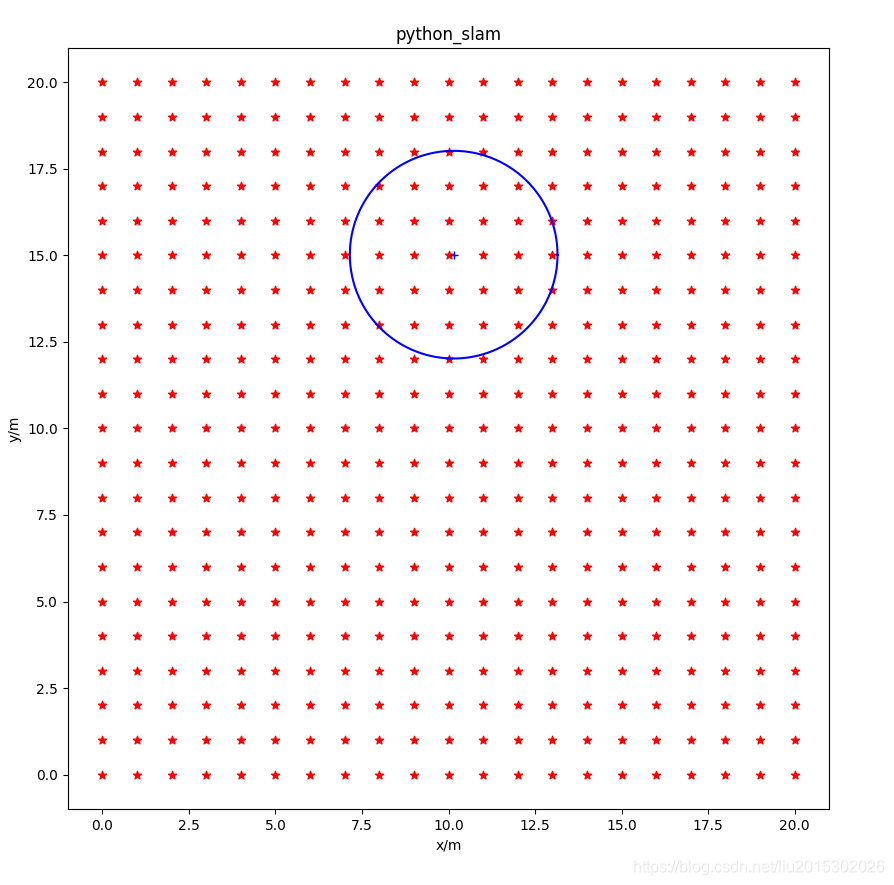
2.1 坐标系

传感器坐标系用\(S\)表示，全局坐标系用\(G\)表示。
设地图中有一路标点\(L=(l_x,l_y)\)，当前传感器位姿\(P=(p_x,p_y,\theta)\)，那么有:

\[ L^G=R_{GS}L^S + P^G \]

其中:

\[ R_{GS} = \left[\begin{matrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{matrix} \right] \]

2.2 运动模型

设输入量为\(u=(u_1,u_2,u_3)\)，将当前时刻雷达局部坐标系中的（\({u}_{1}\),\(u_2\)）点作为下一时刻雷达的位置：

\[ \left[\begin{array}{cc} {x} \\ {y} \end{array} \right] = \left[\begin{array}{cc} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right] \left[\begin{array}{cc} {u}_{1} \\ {u}_{2} \end{array}\right] + \left[\begin{array}{cc} {x} \\ {y} \end{array} \right] \]

其方位变化为:

\[ {\theta} = {\theta} + {u}_{3} \]

2.3 观测模型

设观测到的路标点L的状态为(\({{l}_{x}}^{G}\)，\({{l}_{y}}^{G}\))，当前时刻传感器位姿状态为\((p_x^G,p_y^G)\)，观测方程如下：

\[ \left[\begin{array}{cc} z_1 \\ z_2 \end{array} \right] = {\left[\begin{array}{cc} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right]}^{-1} \left(\left[\begin{array}{cc} {{l}_{x}^{G}} \\ {{l}_{y}^{G}} \end{array} \right] - \left[\begin{array}{cc} {p_x^G} \\ {p_y^G} \end{array} \right]\right)+ \left[\begin{matrix} v_1 \\ v_2 \end{matrix}\right] \]

\[ v_1 = N(0,\sigma_1) \]

\[ v_2 = N(0,\sigma_2) \]

3. 技术方案

3.1 前端跟踪

前端跟踪的主要目的主要有两个：

（1）状态数据关联

（2）求解新状态的初始值。

这里的数据关联可以根据观测信息中的路标点id号来建立；这里主要讨论状态初始值估计。

算法思路：先固定旧状态的估计值，然后通过数据关联的结果来建立关于机器人新位姿状态的误差函数，得到新位姿的初始估计；之后根据新位姿，根据观测方程，直接得到新地图点状态的初始估计值。

% 假设L_i是旧状态中的一个路标点的状态，其估计值已知为\((l_{ix}^G,l_{iy}^G)\)，设当前新位姿状态为\(P_j = (p_{jx},p_{jy},\theta_j)\)，前观测值已知为\(m_{ij}=(m_{ijx},m_{ijy})\)那么有如下关系：
设当前新增机器人位姿P状态为\((p_x^G,p_y^G,\theta)\)，在当前时刻可以观测到的一个旧路标点L，其状态为\(({{l}_{x}}^{G}\)，\({{l}_{y}}^{G})\)，对其的观测为\(M=(z_1,z_2)\)则可以构建下面粗糙的优化函数：

\[ || \left[\begin{array}{cc} z_1 \\ z_2 \end{array} \right] - {\left[\begin{array}{cc} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right]}^{-1} \left(\left[\begin{array}{cc} {{l}_{x}^{G}} \\ {{l}_{y}^{G}} \end{array} \right] - \left[\begin{array}{cc} {p_x^G} \\ {p_y^G} \end{array} \right]\right) ||_2 \]

进而可以转换为下面线性最小二乘问题：

\[ \left[\begin{matrix} 1 & 0 & l_x^G & -l_y^G \\ 0 & 1 & l_y^G & l_x^G \end{matrix}\right] \left[\begin{matrix} p_x^G \\ p_y^G \\ cos\theta \\ sin\theta \end{matrix}\right] = \left[\begin{matrix} z_1 \\ z_2 \end{matrix}\right] \]

我们的目标就是估计\((p_x^G,p_y^G,cos\theta,sin\theta)\)，成功跟踪一个点就可以增加两个约束，跟踪的点越多，越精确，但也越耗时，代码中使用五点法，左侧矩阵为\(10\times4\)，并采用LM算法。

上述这样做法其实不是太好，因为建立的误差方程不能将测量误差的协方差引入。会导致不能“平等地”优化每一个变量。当然最一般地做法是和后端优化一样，建立形如\(||z-h(\xi)||_{\Sigma_z}\)，这样的误差函数。

前段是提供一个初始值，所以够用就行了，况且这里的数据关联是确定的，没有任何外点，后端优化会充分弥补前端的不足。

3.2 滑动窗口优化

3.2.1 图结构

SLAM状态之间的关系可以用一个图来表示，如下图所示：

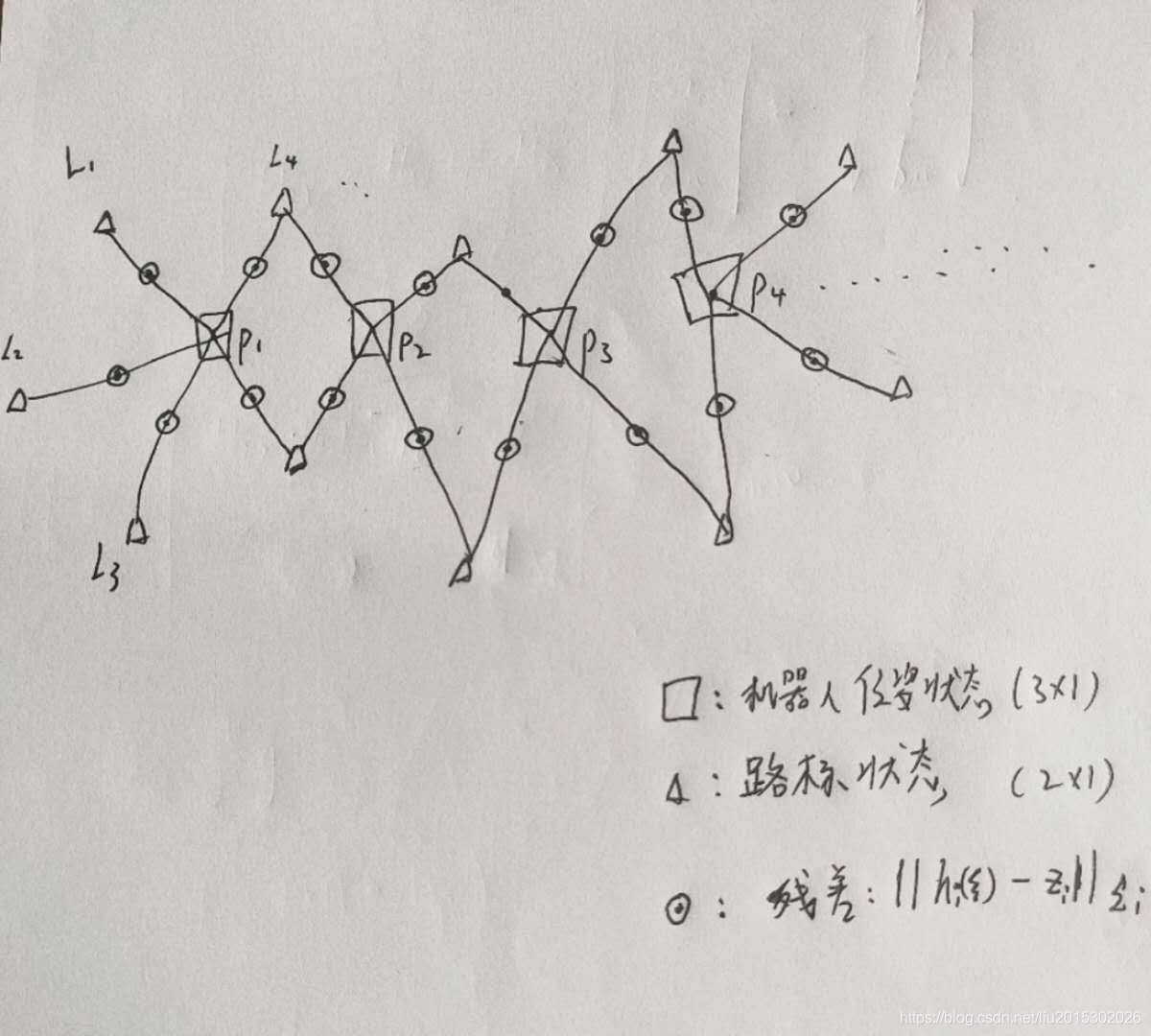
随着机器人不断探索新的环境，这个图也就不断扩大，我们这里把这个图称作一个状态窗口。

设窗口内的一次观测\(z_i=(\alpha_i,s_i)\)，全部状态量为\(\xi\)，\(n\)维，那么残差项\(e_i(\xi)=h_i(\xi)-z_i\)：
用前面介绍的LM法计算，有：

\[ J^T\Sigma_e^{-1}J\delta \xi = -J^T\Sigma_e^{-1}e(\xi) \]

假设有\(m\)次观测，那么上式可以展开为：

\[ \left(J_1^T\Sigma_{e_1}^{-1}J_1+J_2^T\Sigma_{e_2}^{-1}J_2\dots+J_m^T\Sigma_{e_m}^{-1}J_m\right)\delta \xi =-J_1^T\Sigma_{e_1}^{-1}e_1(\xi)-J_2^T\Sigma_{e_2}^{-1}e_2(\xi)\dots-J_m^T\Sigma_{e_m}^{-1}e_m(\xi) \]

\[ J_i(\xi) =\left[\begin{matrix} \frac {\partial e_i(\xi)} {\partial \xi_1} \dots \frac {\partial e_i(\xi)} {\partial \xi_n} \end{matrix}\right] \]

就这样，在不断得到新的观测时，我们不断将新观测引入的\(J_i^T\Sigma^{-1}_{e_i}J_i\)和\(-J_i^T\Sigma_{e_i}^{-1}e_i(\xi)\)加入到求解方程两侧中，进而迭代优化。
\subsubsection{观测模型线性化}

这一节主要内容是求\(J_i(\xi)\):

\[ J_i(\xi) =\left[\begin{matrix} \frac {\partial e_i(\xi)} {\partial \xi_1} \dots \frac {\partial e_i(\xi)} {\partial \xi_n} \end{matrix}\right] =\left[\begin{matrix} 0 & \dots & \frac {\partial e_i(\xi)} {\partial P^G} & \dots & \frac {\partial e_i(\xi)} {\partial L^G} & \dots & 0 \end{matrix}\right]_{2\times n} \]

对机器人位置状态的子雅克比矩阵：

\[ \frac{\partial e_i(\xi)}{\partial P^G} = \left[\begin{matrix} \frac {\partial e_i^{\alpha}(\xi)} {\partial p_x^G} & \frac {\partial e_i^{\alpha}(\xi)} {\partial p_y^G} & \frac {\partial e_i^{\alpha}(\xi)} {\partial \theta} \\ \frac {\partial e_i^{s}(\xi)} {\partial p_x^G} & \frac {\partial e_i^{s}(\xi)} {\partial p_y^G} & \frac {\partial e_i^{s}(\xi)} {\partial \theta} \end{matrix}\right]_{2\times 3} \]

对地图点位置状态的子雅克比矩阵：

\[ \frac{\partial e_i(\xi)}{\partial L^G} = \left[\begin{matrix} \frac {\partial e_i^{\alpha}(\xi)} {\partial l_x^G} & \frac {\partial e_i^{\alpha}(\xi)} {\partial l_y^G} \\ \frac {\partial e_i^{s}(\xi)} {\partial l_x^G} & \frac {\partial e_i^{s}(\xi)} {\partial l_y^G} \end{matrix}\right]_{2\times 2} \]

关于上述两个子雅克比矩阵在\(J_i(\xi)\)中的摆放位置是根据状态向量\(\xi\)里的子状态摆放次序决定的。这里需要先规定一下各个状态量在\(\xi\)中的摆放次序。

假设滑动窗口中存在连续m个时刻的机器人位置状态\((P_1^G,P_2^G,\dots P_m^G)\)，每个时刻\(i\)观测到的新地图点的状态（注意是新的地图点）为\((L^G_1(i),L^G_2(i),\dots,L^G_{n_i}(i))\)，那么这里把状态量的次序规定如下，当然这样规定更是为了以后Marginalization的时候方便对矩阵操作：

\[ \xi = \left[\begin{matrix} P_1^G \\ L_1^G(1) \\ L_2^G(1) \\ \vdots \\ L_{n_1}^G(1) \\ P_2^G \\ L_1^G(2) \\ L_2^G(2) \\ \vdots \\ L_{n_2}^G(2) \\ \vdots \\ P_m^G \\ L_1^G(m) \\ L_2^G(m) \\ \vdots \\ L_{n_m}^G(m) \\ \end{matrix} \right]= \left[\begin{matrix} \xi_1 \\ \xi_2 \\ \vdots \\ \xi_m \end{matrix}\right] \]

下面等式关系定义了观测函数\((\alpha,s)^T=h(P^G,L^G)\)：

\[ \left[\begin{array}{cc} {{l}_{x}^{S}} \\ {{l}_{y}^{S}} \end{array} \right] = {\left[\begin{array}{cc} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right]}^{-1} \left(\left[\begin{array}{cc} {{l}_{x}^{G}} \\ {{l}_{y}^{G}} \end{array} \right] - \left[\begin{array}{cc} {p_x^G} \\ {p_y^G} \end{array} \right]\right)+ \left[\begin{matrix} v_1 \\ v_2 \end{matrix}\right] \]

下面具体求\(\frac{\partial e_i(\xi)}{\partial P^G}\)和\(\frac{\partial e_i(\xi)}{\partial L^G}\)：

\[ \frac{\partial e_i(\xi)}{\partial P^G} = \frac{\partial h_i(\xi)}{\partial P^G} \]

\[ \frac{\partial e_i(\xi)}{\partial L^G} = \frac{\partial h_i(\xi)}{\partial L^G} \]

\[ \frac{\partial h_i(\xi)}{\partial P^G} = \left[\begin{matrix} \frac{\partial h_{ix}}{\partial p^G_x} & \frac{\partial h_{ix}}{\partial p^G_y} & \frac{\partial h_{ix}}{\partial \theta} \\ \frac{\partial h_{iy}}{\partial p^G_x} & \frac{\partial h_{iy}}{\partial p^G_y} & \frac{\partial h_{iy}}{\partial \theta} \end{matrix}\right]=\left[\begin{matrix} -cos\theta & -sin\theta & {(p_x^G-l_x^G)sin\theta+(l_y^G-p_y^G)cos\theta} \\ sin\theta & -cos\theta & {(p_x^G-l_x^G)cos\theta+(p_y^G-l_y^G)sin\theta} \end{matrix}\right] \]

\[ \frac{\partial h_i}{\partial L^G}=\left[\begin{matrix} \frac{\partial h_{ix}}{\partial l^G_x} & \frac{\partial h_{ix}}{\partial l^G_y} \\ \frac{\partial h_{iy}}{\partial l^G_x} & \frac{\partial h_{iy}}{\partial l^G_y} \end{matrix}\right]= \left[\begin{matrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{matrix}\right] \]

3.2.2 舒尔补与边缘化

显然，随着时间的推移，系统的状态越来越多，\(H\)阵越来越大，使得计算量越来越大；所以这里采用滑动窗口法来控制优化规模在一个确定的区间内。

滑动窗口法的一个关键是如何处理丢弃的观测，是把它直接丢掉，还是转化为对剩余状态量的约束。

很直观的想法是把最近\(n\)帧的机器人位姿变量以及与其有关联的地图点状态留下，其余都扔了，重新建立新的误差方程。很明显，这里相当于把一些约束条件扔了，使得信息丢失一部分，所以这里使用边缘化技术来得到丢掉的观测构成的先验。

这里采用的策略是：对于刚刚优化完成的滑动窗口，如果\(n\)超过规定的最大位姿数量，那么就把最早的一个位姿状态以及和其有观测关系的所有地图点状态都边缘化掉，记为\(\xi_m\)，其余剩下的状态记为\(\xi_r\)。

\(\xi_m\)对应的观测与\(\xi\)构成的最小二乘问题为：

\[ (\lambda I + H) \delta\xi = b \]

也即为：

\[ (\lambda I + \left[\begin{matrix} H_{mm} & H_{mr} \\ H_{rm} & H_{rr} \end{matrix}\right]) \left[\begin{matrix} \delta \xi_m \\ \delta \xi_r \end{matrix}\right] = \left[\begin{matrix} b_m \\ b_r \end{matrix}\right] \]

利用舒尔补，那么可以得到：

\[ (\lambda I_r + H_{rr} - H_{rm}*(\lambda I_m + H_{mm})^{-1}*H_{mr} )\delta\xi_r = b_r - H_{rm}*(\lambda I_m + H_{mm})^{-1}*b_m \]

这样我们就得到了丢弃观测中的先验信息：

\[ H_{prior} = \lambda I_r + H_{rr} - H_{rm}*(\lambda I_m + H_{mm})^{-1}*H_{mr} \]

\[ b_{prior} = b_r - H_{rm}*(\lambda I_m + H_{mm})^{-1}*b_m \]

在下一次滑窗优化时候，其滑窗内的观测与\(\xi\)构成新的最小二乘问题为：

\[ (\lambda I + \left[\begin{matrix} H_{rr} & H_{r,new} \\ H_{new,r} & H_{new,new} \end{matrix}\right]) \left[\begin{matrix} \delta \xi_r \\ \delta \xi_{new} \end{matrix}\right] = \left[\begin{matrix} b_r \\ b_{new} \end{matrix}\right] \]

加上先验即为：

\[ (\lambda I + \left[\begin{matrix} H_{rr} & H_{r,new} \\ H_{new,r} & H_{new,new} \end{matrix}\right] + H_{prior}) \left[\begin{matrix} \delta \xi_r \\ \delta \xi_{new} \end{matrix}\right] = \left[\begin{matrix} b_r \\ b_{new} \end{matrix}\right] + b_{prior} \]

3.2.3 FEJ保证系统一致性

其实我们上面边缘化的策略已经保证了\(FEJ\)，因为我们把最早的一个位姿状态以及和其有观测关系的所有地图点状态都边缘化掉，这保证了误差函数不会在两个不同的点处线性化，也就保证了先验项\(H_{prior}\)与当前\(H\)不会冲突。

4. 系统设计

4.1 数据类型

Landmark类：用于仿真实际2D环境，存放环境各种信息。

Movemodel类：用于仿真机器人运动，存放机器人运动的真实位置，为提供给观测类。

Measure类：存放测量信息，获取测量信息。

Frame类：这是为位姿态节点设计的抽象类，其主要目的有两个，一个是存放当前位姿，另一个是建立与地图点的联系。

Mappoint类：为landmark设计的抽象类，其主要目的也有两个，一个存放估计的地图点位置，一个是建立与frame联系

Gaussnewton类：这个类是一个线性最小二乘求解器。

Draw类：里面存放主要抽象类的地址，显示想要的数据。

Slidewindowgraph类：滑动窗口类，是最重要的数据成员，其利用上述数据类型，完成前端数据关联，后端滑窗优化。

4.2 代码逻辑

系统整个过程的核心就是维护Slidewindowgraph这个类,具体从main.py开始看，代码清晰，模块分明。

5. 仿真结果

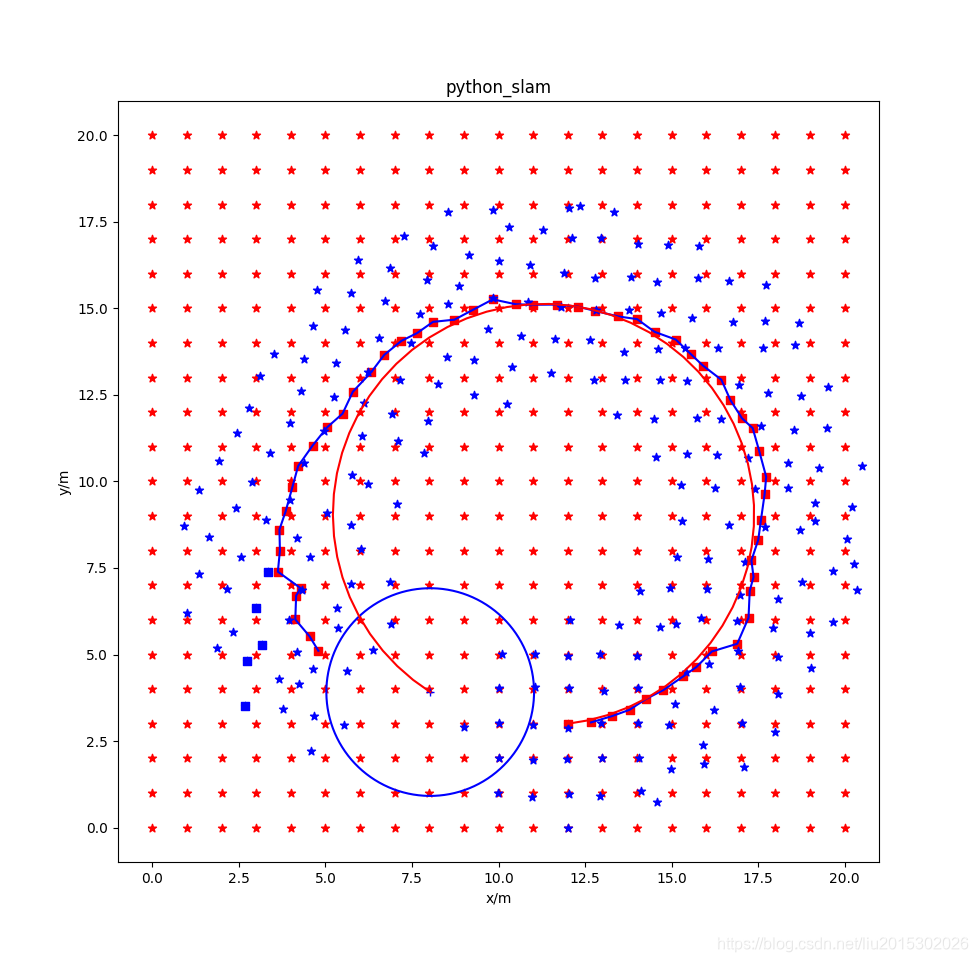
仅仅前端跟踪，后端优化去掉。打开slidewindow_graph.py，注释掉函数def Update(self, measure)中的self.Optimize_graph()，其运行结果为：

使用后端优化，但是不使用滑动窗口，状态量都保存下来。打开slidewindow_graph.py，注释掉函数def Optimize_graph(self)中的 self.Get_prior()和self.Cut_window()，其运行结果为：

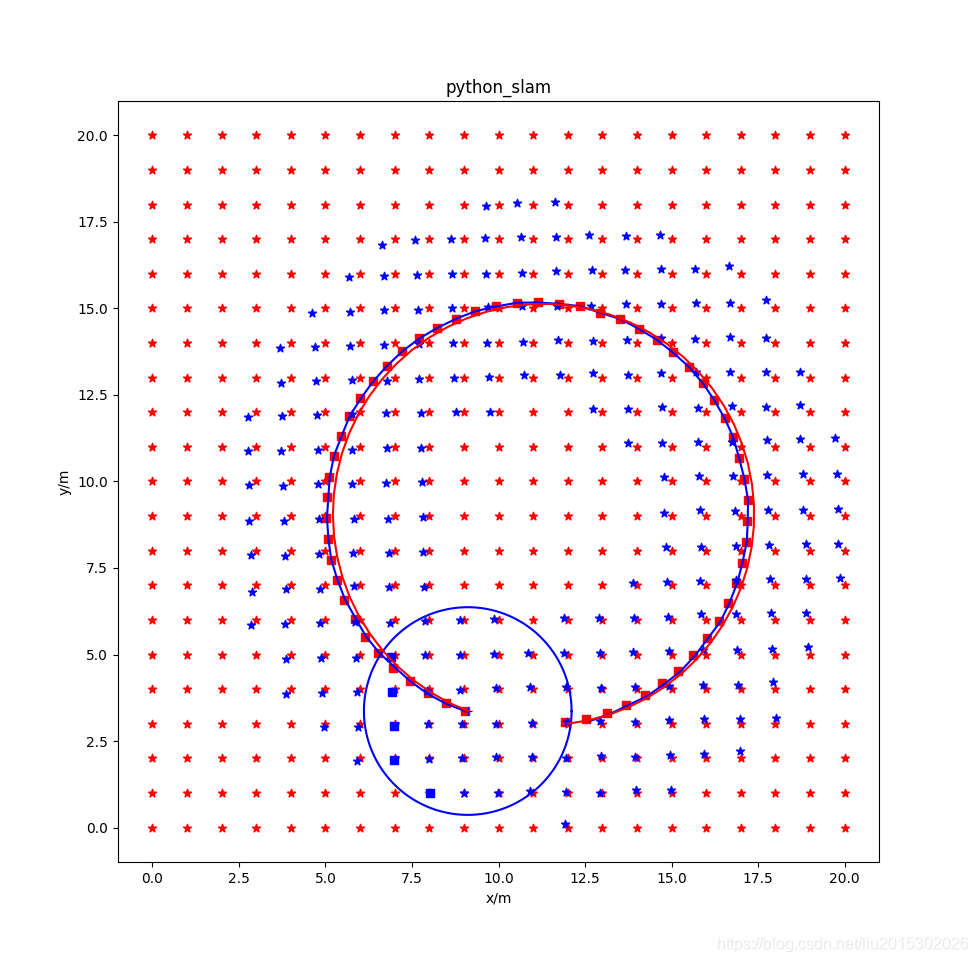
使用后端优化，使用滑动窗口，但是不使用先验信息。打开slidewindow_graph.py，注释掉函数def Optimize_graph(self)中的 self.Get_prior()，其运行结果为：

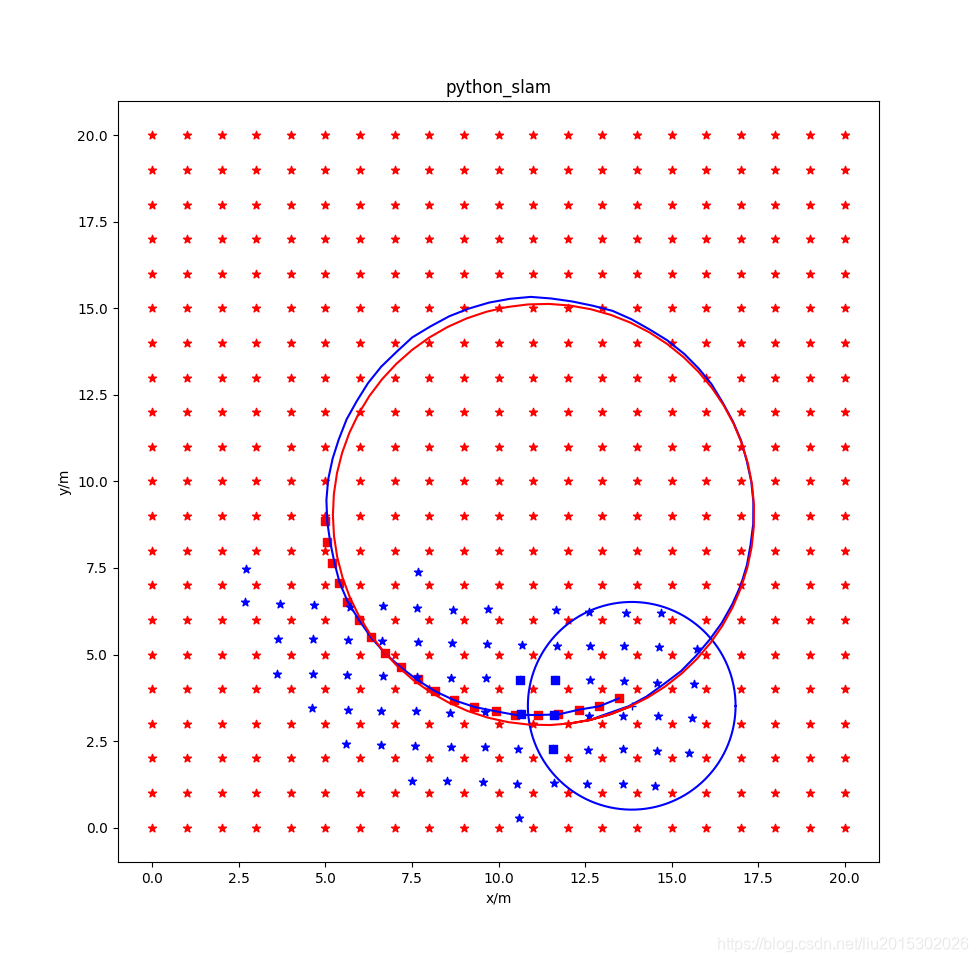
使用后端优化，使用滑动窗口，使用先验信息。其运行结果为：

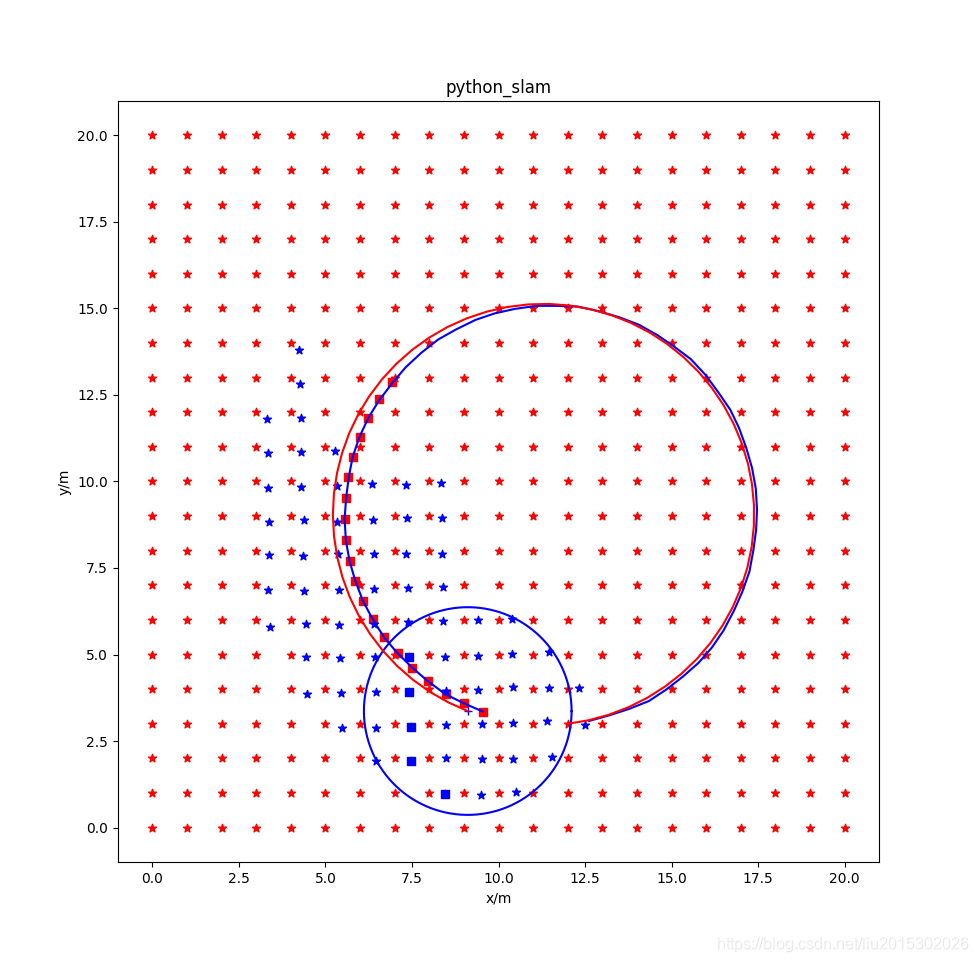
图中各元素说明：红色星形为环境中固定的landmark，蓝色点是当前状态窗口中landmark位置的估计值，红色方形是当前状态窗口中机器人位姿估计值，蓝色方形是前后帧之间跟踪用的五个状态点。

从仿真结果看，不使用滑动窗口的全局优化效果最好；使用滑动窗口时，用不用先验效果不太明显；仅仅使用前端五点法跟踪，效果非常差。