欧拉角研究

　　对于在三维空间里的一个参考系，任何其它坐标系的取向，都可以用三个欧拉角来表现。参考系又称为实验室参考系，是静止不动的。而坐标系则固定于刚体，随着刚体的旋转而旋转。
　　欧拉角是用来表示三维坐标系中方向和方向变换的。我们平时说的欧拉角其实还可以细分为欧拉角(Euler-angles)和泰特布莱恩角(Tait-Bryan-angles)，这两种方法都利用了笛卡尔坐标系的三轴作为旋转轴，主要区别在于选取顺序。欧拉角的选取顺序有  这6种，可见选取顺序是a,b,a这样的顺序，也就是绕a轴旋转某角度后，绕新生成的b轴旋转一个角度，最后绕两次旋转以后的a轴再旋转一个角度，以此表示最终的方向。泰特布莱恩角的旋转轴选取有  这6种，也就是历遍笛卡尔坐标系的三轴，比如我们最常见到的Roll-Pitch-Yaw角就是其中  的情况。但这两种方法，其实都是在空间中用最直观的方式和最少的参数表示任意方向的通用方法。

（一）zxz顺序欧拉角

如下图所示。设定xyz-轴为参考系的参考轴XYZ-轴为物体上的坐标系轴。称xy-平面与XY-平面的相交为交点线，用英文字母（N）代表。zxz顺规的欧拉角可以静态地这样定义

 

α 是x-轴与交点线的夹角，

β 是z-轴与Z-轴的夹角，

γ 是交点线与X-轴的夹角。

(可以证明Z,z轴与N是垂直的)

对于夹角的顺序和标记，夹角的两个轴的指定，并没有任何常规。不同的作者会用不同组合的欧拉角来描述，或用不同的名字表示同样的欧拉角。因此，使用欧拉角前，必须先做好明确的定义。

这个过程中新生成的坐标系  可以通过运算由原坐标系  得到:

其中，矩阵M表示了上面三次旋转的总过程。我们简单推一下:

以上欧拉角  的情况。

　　用欧拉角表示方向（或者说，方向变换）只需要用到三个参数，即三个旋转角度（因为坐标轴是旋转轴，所以不用增加特别的参数描述旋转轴），这样做有一个非常大的优点，就是表述清晰易懂。但随之而来的有一个很重要的问题，简单来说就是，当给定了欧拉角以后，我们很容易找到欧拉角表述的方向，但是当我们获得了一个方向以后，却不一定能唯一写出目标欧拉角来描述旋转，三维空间中的任意一个方向都可以通过至少两种不同欧拉角表示。比如说（0,0,0）和(1,0,-1)在以上欧拉角选取顺序上，是表示同一个目标方向。

（二）x,y,z顺序欧拉角

空间中有三个旋转欧拉角α，β，γ，选取顺序为x，y，z，可以通过构建旋转矩阵Rx，Ry，Rz得到旋转矩阵R=Rz（γ）Ry（β）R_x（α），空间某点m(x,y,z)在新的坐标系下的坐标为：Rm(x,y,z)。

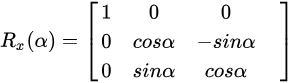
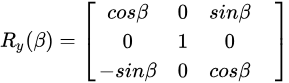
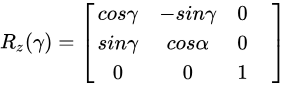
旋转矩阵计算欧拉角公式：

 

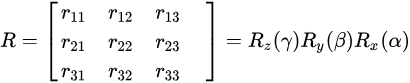
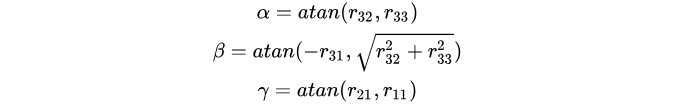
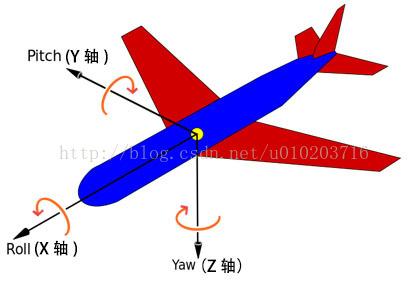
俯仰角θ（pitch）：围绕Y轴旋转的角度。   

偏航角ψ（yaw）：围绕Z轴旋转的角度。       

滚转角Φ（roll）：围绕X轴旋转的角度。

                                                                                                  

　　现在我们如果想实现一个旋转，只要依次绕三个轴转对应的角度就可以实现。但是由于万向节死锁的问题，简单的说就是一旦选择±90°作为pitch角，就会导致第一次旋转和第三次旋转等价，整个旋转表示系统被限制在只能绕竖直轴旋转，丢失了一个表示维度。比如说(5,90,10)与(1,90,14)表示相同的方向，此时绕X轴旋转与绕Z轴旋转没有区别。我们获得一个方向后不一定能得到确定的欧拉角来描述它。所以在通常有关旋转的应用场景中基本不使用欧拉角来旋转，而使用四元数Quaternion,因为四元数可以实现平滑插值。

  

（三）欧拉角万向锁效应

在游戏中，当角色旋转的动画触发时，角色就会做一系列连续的旋转变换，每一个变换都要用一组欧拉角来表示，但是不可能吧每一个方位的欧拉角都存储起来，因此动画师定义了一系列关键帧，指定关键帧处角色的方位（用一组欧拉角描述），然后计算机根据时间t对这几组欧拉角进行插值，得到一系列欧拉角。

如果pitch不是±90°，就不会出现万向锁现象，插值后的一系列欧拉角完全可以刻画出我们所期望的角色旋转路径。

 如果某个关键帧的pitch即绕第二个轴的旋转为90°，就会遇到万向锁

 为了能有一个感性的认识，还是以手机为例,下面我指定了四个关键帧，四个关键帧处手机的方位分别用R0,R1,R2,R3四组欧拉角表示(逆时针为正方向，右手法则）：

（注意R0处的物体坐标系与世界坐标系的指向是相同的，我假定z轴向上，x轴p向右，y轴指向自己的胸口）

                  绕z轴旋转角度       绕y轴旋转角度      绕x轴旋转角度

R0:                     0                              0                       0

R1:                    90                             0                       0

R2:                    90                            90                      0

R3:                     0                              0                       90

请先分别对手机做这四个变换，然后记住手机的这四个方位，想象一下你“期望”的连续的动画应该是什么样子的。

但实际情况是否是这样的呢？

你可以自己尝试对这个四个方位角插值，然后进行旋转，看看得到的路径是否和上述我们所期望的相同。

以下是我的尝试：

 求出R0 到R1以及R1到R2的插值，然后旋转，完全符合上面的路径。但是再求出R2到R3的几个插值后，旋转得到的路径与期望不符。比如这两个插值：

   z：60  y：60  x：30

   z:    45     y:45    x:45

做这两个旋转，你会发现手机与桌面不垂直，也就是R2到R3的路径与期望的发生了偏移（本来R2到R3的过程按照预想应该是手机一直与桌面垂直）。

其实这是由于欧拉角插值的不光滑引起的。通俗的讲两个欧拉角插值得到的新欧拉角，不一定在你想要的轨迹上。

总结：如果动画师在某个关键帧处指定了会引发万向锁的方位，则下一个关键帧的方位一旦超出了万向锁的约束范围，则这两个关键帧之间的路径就可能会发生偏移，反映在角色动画上是旋转偏移，反映在镜头控制上就是镜头抖动。

要获得路径偏移的感性认识，可以参考这个视频：这个视频和我的描述有些不同，该视频使用一个称为万向节的奇怪装置解释的，而我是直接用的物体坐标系但路径偏移都是一样的。

 

 视频网址：http://v.youku.com/v_show/id_XNzkyOTIyMTI=.html

疑问：当第二次旋转角不是90度时，两帧图片插值是否得到不同的轨迹？

欧拉角插值问题分析。

事实1 . 单个欧拉角能够正确表示旋转无论死锁还是不死锁。但是当两个欧拉角插值的时候，由于死锁的存在，导致插值后的欧拉角表示的旋转与原始的两个欧拉角表示的旋转差异很大。 

事实2. 一种旋转可以用多种欧拉角表示。例如，x角度为100，与x角度为460其实是一样的。X角度为-179其实和+179很接近。更有甚者，当出现死锁的时候，同一种旋转有无数种欧拉角表示。具体方法参照文章Computing Euler angles from a rotation matrix

事实4. 当欧拉角接近死锁的时候会引起抖动。例如48.5557    82.8384       48.0888以及   141.922       81.0177             142.027.这两个欧拉角其实非常相近，但是除了y角之外其余两个坐标差异比较大。因为两个欧拉角的y旋转角度都接近90°了，越靠近90°，y轴的微小变动就对xz两个角度影响非常大，所以进行插值的时候直接进行插值会引起抖动。例如上面的插值结果可能为5.23894            90.9103       5.05811，这个结果与上面两个原始角度所表达的方向都不一样。

参考文献：

www.cnblogs.com/xiaoxiaoqingyi/p/6932008.html

www.zhihu.com/question/47736315/answer/236808639

www.cnblogs.com/tclikang/archive/2012/11/29/2794687.html