算法笔记_053:最优二叉查找树(Java)
目录
1 问题描述
在了解最优二叉查找树之前,我们必须先了解何为二叉查找树?
引用自百度百科一段讲解:
二叉排序树(Binary Sort Tree)又称二叉查找树(Binary Search Tree),亦称二叉搜索树。
二叉排序树或者是一棵空树,或者是具有下列性质的二叉树:
(1)若左子树不空,则左子树上所有结点的值均小于或等于它的根结点的值;
(2)若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
(3)左、右子树也分别为二叉排序树;
在二叉查找树的基础上,引出了一个最优二叉查找树的问题:它在查找树中所有节点的平均键值比较次数是最低的。(PS:如若对于最优二叉查找树的定义理解还是有点模糊,可以参考本文最后给出的参考资料中的链接)
2 解决方案
本文具体编码思想参考自《算法设计与分析基础》第三版,具体如下(PS:对于文中的具体思想,楼主自己是前后看了三四遍才整明白其具体思想,竟无语吟噎......,如若对于下面贴出的书中介绍无法理解,可以参考文末给出的参考资料的链接中,一位网友的博客讲解哦):
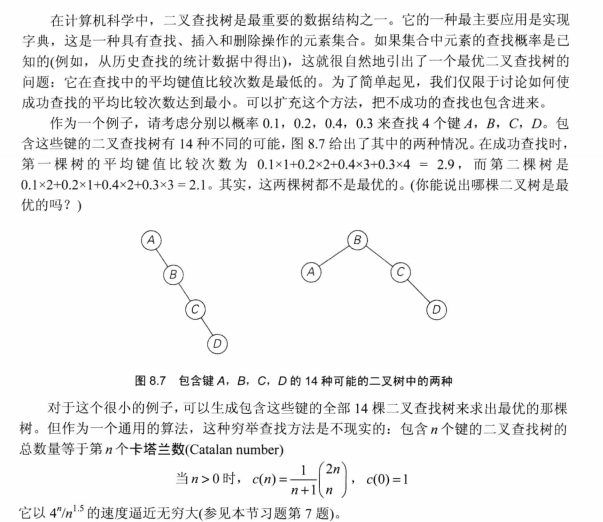



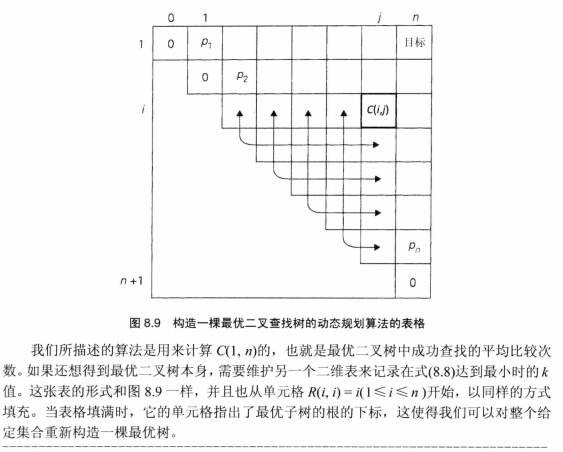

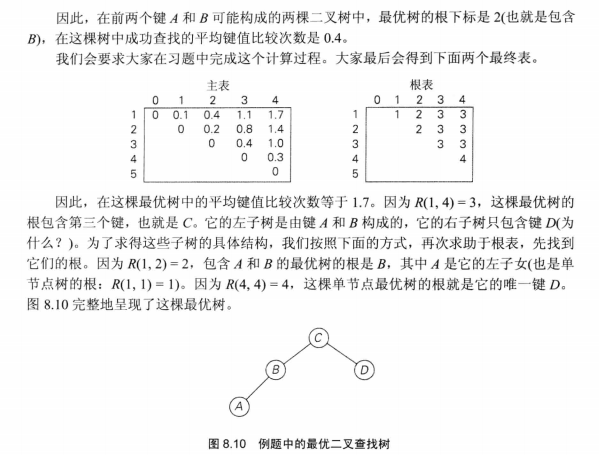
具体代码如下:
package com.liuzhen.chapter8; public class OptimalBST { /* * 参数P:表示1~n个节点的查找概率。其中P[0] = 0,无意义 * 函数功能:返回在最优BST中查找的平均比较次数主表C[][],以及最优BST中子树的根表R */ public void getBestTree(double[] P) { int lenP = P.length; double[][] C = new double[lenP+1][lenP]; //保存最有BST的成功查找的平均比较次数 int[][] R = new int[lenP+1][lenP]; //保存最优BST中子树的根表R for(int i = 1;i < lenP;i++) { C[i][i] = P[i]; R[i][i] = i; } for(int d = 1;d < lenP-1;d++) { for(int i = 1;i < lenP-d;i++) { int j = i + d; double minval = Double.MAX_VALUE; //以double类型的最大值,表示minval趋向无穷大 int kmin = 0; for(int k = i;k <= j;k++) { if(C[i][k-1] + C[k+1][j] < minval) { minval = C[i][k-1] + C[k+1][j]; kmin = k; } } R[i][j] = kmin; double sum = P[i]; for(int s = i+1;s <= j;s++) sum += P[s]; C[i][j] = minval + sum; } } System.out.println("在最优BST中查找的平均比较次数依次为:"); for(int i = 1;i < C.length;i++) { for(int j = 0;j < C[0].length;j++) System.out.printf("%.1f\t",C[i][j]); System.out.println(); } System.out.println("在最优BST中子树的根表R为:"); for(int i = 1;i < R.length;i++) { for(int j = 0;j < R[0].length;j++) System.out.print(R[i][j]+"\t"); System.out.println(); } } public static void main(String[] args) { OptimalBST test = new OptimalBST(); double[] P = {0,0.1,0.2,0.4,0.3}; test.getBestTree(P); } }
运行结果:
在最优BST中查找的平均比较次数依次为: 0.0 0.1 0.4 1.1 1.7 0.0 0.0 0.2 0.8 1.4 0.0 0.0 0.0 0.4 1.0 0.0 0.0 0.0 0.0 0.3 0.0 0.0 0.0 0.0 0.0 在最优BST中子树的根表R为: 0 1 2 3 3 0 0 2 3 3 0 0 0 3 3 0 0 0 0 4 0 0 0 0 0
参考资料:
1.《算法设计与分析基础》第3版 Anany Levitin 著 潘彦 译
每天一小步,成就一大步

