最优运输（Optimal Transfort）：从理论到填补的应用
目录
3.1 离散测度 (Discrete measures)
3.2 蒙日(Monge)问题
3.3 Kantorovich Relaxation (松弛的蒙日问题)
3.4 Wasserstein距离
3.5 最优运输问题初解
3.6 熵(Entropic)正则化
3.7 Sinkhorn算法 (NIPS, 2013)
引言
最优运输（Optimal Transport）近年来引起了广大学者的研究兴趣，并在NIPS和ICML等机器学习顶级会议频繁出现。然而，最优运输的基本理论对于初学者来说，并不友好：初看理论，感觉全是晦涩难懂的数学推理公式，让很多读者有点望而却步的感觉。此外，目前国内关于最优运输理论的研究还比较初步，相关中文资料也比较匮乏。因此，笔者对自己最近几天在网上博客、论文和视频等资料的学习过程进行了初步整理，希望对后续的初学者提供一点帮助。
我的入门体验：最优运输相关理论的代码库已比较丰富（需要代码，可以去github上搜索，或者检索关于最优运输的热门顶会论文，基本都有开源代码），并且核心理论也没那么复杂，或者说只要你认真阅读完本文，我相信你应该能够较顺畅地把最优运输理论应用到你的实际应用中了。
1 背景
最优运输问题最早是由法国数学家加斯帕德·蒙日(Gaspard Monge)在19世纪中期提出，它是一种将给定质量的泥土运输到给定洞里的最小成本解决方案。这个问题在20世纪中期重新出现在坎托罗维奇的著作中，并在近些年的研究中发现了一些令人惊讶的新进展，比如Sinkhorn算法。最优运输被广泛应用于多个领域，包括计算流体力学，多幅图像之间的颜色转移或图像处理背景下的变形，计算机图形学中的插值方案，以及经济学、通过匹配和均衡问题等。此外，最优传输最近也引起了生物医学相关学者的关注，并被广泛用于单细胞RNA发育过程中指导分化以及提高细胞观测数据的数据增强工具，从而提高各种下游分任务的准确性和稳定性。
当前，许多现代统计和机器学习问题可以被重新描述为在两个概率分布之间寻找最优运输图。例如，领域适应旨在从源数据分布中学习一个训练良好的模型，并将该模型转换为采用目标数据分布。另一个例子是深度生成模型，其目标是将一个固定的分布，例如标准高斯或均匀分布，映射到真实样本的潜在总体分布。在最近几十年里，OT方法在现代数据科学应用的显著增殖中重新焕发了活力，包括机器学习、统计和计算机视觉。
2 什么是最优运输？
参考资料[1]的见解：就是把A数据迁移到B。你可以理解成两堆土，从A土铲到另外一个地方，最终堆成B土。就像是以前初中学的线性规划一样的：3个城市（A, B, C）有1, 0.5, 1.5吨煤，然后要运到2个其他城市，这两个城市(C, D)分别需要2，1吨煤。然后，不同城市到不同的费用不同，让你算最优运输方案和代价。
Jingyi Zhang等人[2]的综述表明：假设一个操作者经营着n个仓库和m个工厂。每个仓库都包含一定数量的有价值的原材料（即工厂正常运行所需要的资源），而且每个工厂对原材料都有一定的需求。假设n个仓库中资源的总量等于m个工厂对原材料的总需求，运营商的目标是将所有的资源从仓库转移到工厂，从而能够成功地满足工厂的所有需求，并且总运输成本尽可能小。具体如下图1所示的资源分配问题。
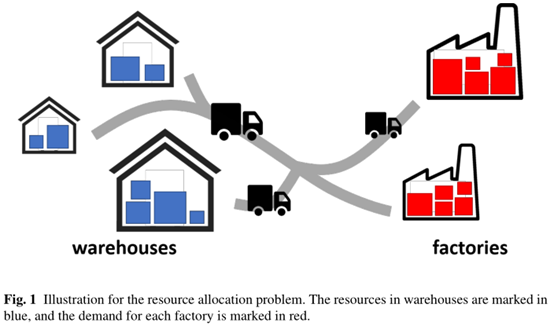
通过上述两个简单的描述，相信大家应该知道什么是最优运输了。在这里，你可能对于该理论还是有一点模糊的感觉。但是，请保持这颗好奇心往下看看具体的基本理论，下文将会结合参考文献[3]（关于最优传输的一本很经典的开源书籍）提供的公式和图例来详细介绍。
3基本概念
3.1离散测度 (Discrete measures)
首先，说一下概率向量（或者称为直方图，英文：Histograms， probability vector）的定义：
上述公式的含义：一个长度为n的数组，每个元素的值在[0, 1]之间，并且该数组的和为1，即表示的是一个概率分布向量。
离散测度：所谓测度就是一个函数，把一个集合中的一些子集（符合上述概率分布向量）对应给一个数[4]。具体公式定义如下：
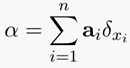
上述公式含义：以a_i为概率和对应位置x_i 的狄拉克δ函数值乘积的累加和。下图很好地阐述了一组不同元素点的概率向量分布：
上图中红色点是均匀的概率分布，蓝色点是任意的概率分布。点状分布对应是一维数据的概率向量分布，而点云状分布对应的是二维数据的概率向量分布。
3.2蒙日(Monge)问题
蒙日(Monge)问题的定义：找出从一个 measure到另一个measure的映射，使得所有c ( x i , y j )的和最小，其中c表示映射路线的运输代价，需要根据具体应用定义。蒙日问题具体的定义公式如下：
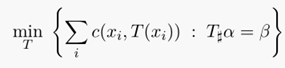
对于上述公式的解释可以采用离散测度来解释，对于两个离散测度：
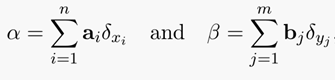
找到一个n维映射到m维的一个映射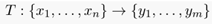
，使得
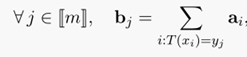
上述映射的示意图如下：
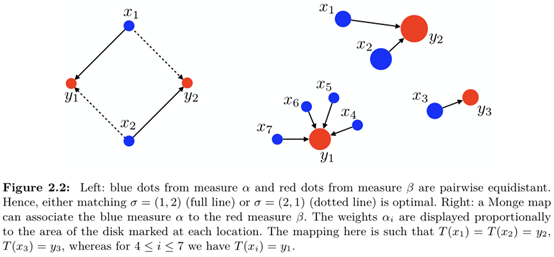
对于上述的映射公式，结合蒙日问题的定义公式，可以归纳如下：
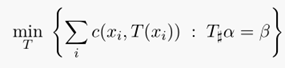
上述公式的含义：通过这个映射T(X_i)的转移，使得转移到b_j的所有a_i的值的和刚好等于b_j（其中要求，所有a_i必须转走，而所有b_j必须收到预期的货物），即我需要多少就给运输转移多少，不能多也不能少。其中c()表示运输代价，T(x_i)表示映射的运输方案。
3.3 Kantorovich Relaxation (松弛的蒙日问题)
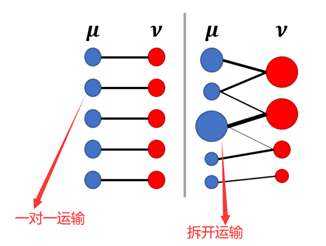
蒙日问题是最优运输的起初最重要的思想，然而其有一个很大的缺点: 从a的所有货物运输到b时，只能采用原始的货物大小进行运算，即不能对原始的货物进行拆开发送到不同目的地。而Kantorovich Relaxation则对蒙日问题进行了松弛处理，即原始的货物可以分开发送到不同目的地，也可以把蒙日问题理解为Kantorovich Relaxation的一个映射运输特例。具体区别可以参考下图[2]。
符合Kantorovich Relaxation的映射运输定义公式如下：
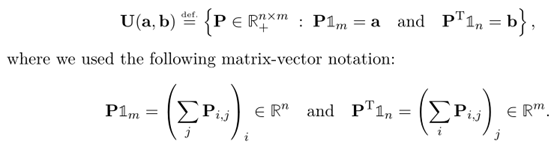
区别于蒙日问题要求映射运输的所有a_i一对一转走到b_j。Kantorovich Relaxation只要求，所有每个a_i中获取能够完全转走，可以是只转给一个b_j，也可以是多个b_j，但是要确保每个b_j只需要收取预期要求的货物即可。简单地描述：行求和对应向量a, 列向量求和对应向量 b.具体的传输示例如下：
最后，Kantorovich Relaxation的最优运输求解公式定义如下：
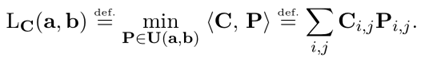
其中P表示符合所有行求和为向量a，所有列求和为向量b的一个映射。Pi,j表示从第i行映射到第j行的元素值，Ci,j表示完成Pi,j元素映射（或者说是运输）的运输代价。
3.4 Wasserstein距离
距离度量是机器学习任务中最重要的一环。比如，常见的人工神经网络的均方误差损失函数采用的就是熟知的欧式距离。然而，在最优运输过程中，优于不同两点之间均对应不同的概率，如果直接采用欧式距离来计算运输的损失（或者说对运输的过程进行度量和评估），则会导致最终的评估结果出现较大的偏差（即忽略了原始不同点直接的概率向量定义）。
针对上述问题，为了对最优运输选择的映射路径好坏进行评估，Wasserstein距离应运而生，其公式和相关引理定义如下：
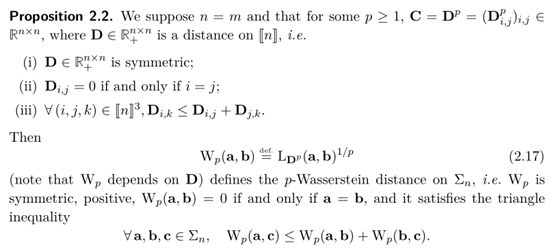
此处的距离计算公式看起来比较复杂，但是实际上该方法已有代码库[5]封装好，只需要把对应的向量a和其包含的概率分布，以及向量b和其包含的概率分布输入到封装好的函数中，即可得到最终的Wasserstein距离。关于此处的介绍和理解，建议参考文末的参考资料[6]，其部分解释可以见下图：
3.5最优运输问题初解
最优运输问题的解是一般是求取Kantorovich Relaxation的解，其可以采用线性规划的标准型来定义和实现求解[7]。了解过线性规划理论知识的同学应该清楚：线性规划求解一般是取可行域内的顶点值，才是最终需求的最优解（最小值或者最大值，具体选取看实际的可行域约束条件）。因此，线性规划的最优解，只可能是可行域表示的可行多面体的一个顶点。
依据参考资料[7]和文献[3]，对于线性规划寻找顶点解时，当判断其是否是一个最优解，需要符合以下条件：如果P是一个顶点解，那么P中有质量流的路径一定不行成一个环。这同时也意味着P中最多只能有n + m − 1条不为零的质量流。具体的示意图如下：
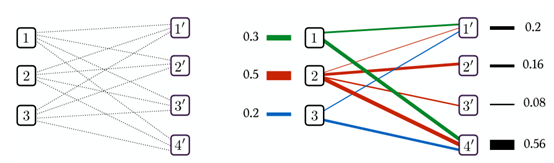
上图每条连线表示一个质量流，但其其中存在环，可知一定不是最优解。这便是求解最优运输的几何解释，更多的示例，请参考文献[3]的3.4节，第43页。
依据上述的思路，采用线性规划求取最优运输的最优解，有学者提出了采用西北角算法，其可以在经过n + m步计算后，搜索出一个U ( a , b )的顶点。更多具体的解释和介绍请见参考资料[8]。
然而采用西北角算法每次的检索结果只有一个顶点，该顶点并不一定是最优解。为了解决该问题，网络单纯形法出现了，该方法通过从可行多面体的一个顶点出发，每一步都到达一个离最优更接近的顶点，逐步达到最优。然而，单纯形的最差复杂度是指数级的，不过它的平均复杂度却非常高效，一般在多项式时间内找到最优解。关于单纯形法的具体更多介绍，请见参考资料[9]。下方给出一个单纯形法迭代求取最优解的示例图，具体的解释可以参考文献[3]的3.5.3节。
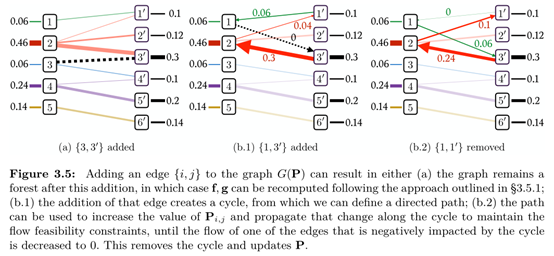
3.6 熵(Entropic)正则化
在大部分应用情况下，求标准Kantorovich Relaxation解是不必要的：如果我们利用正则化，改求近似解，那么最优传输的计算代价就大幅降低了[10]。熵正则化的定义公式如下：
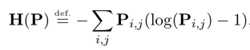
对Kantorovich Relaxation解添加正则化后，求解最优传输问题的定义如下：
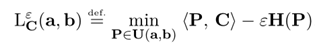
其中参数thegama表示正则化系数，其作用和常用的人工神经网络等方法中的正则化系数一样。其中参数P=diag(u)*K*diag(v)，其中u和v表示映射的一组解，并参数Pi,j满足以下定义：
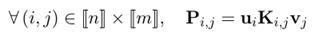
此外，由蒙日问题中定义的所有行的和组成的向量a和所有列的和组成的向量b和求解的映射u，v解的关系如下：
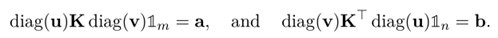
可以推导处如下一个结论，具体的证明推理过程请见参考文献64页[3]。
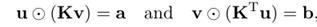
依据参考资料[10]的讲解：正则化鼓励利用多数小流量路径的传输，而惩罚稀疏的，利用少数大流量路径的传输，由此达到减少计算复杂度的目的。具体的解释可以参考下述的示意图：
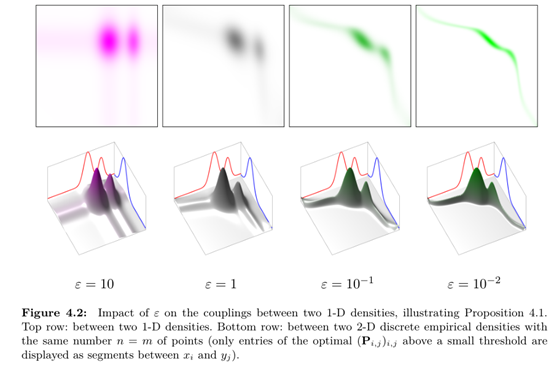
由上图可知，当参数thegama越大时，最优解的耦合程度变得越加稀疏，即不同解之间距离越大。通过熵正则化的处理，求取近似解的过程，能够有效降低获取理想解的时间。
3.7 Sinkhorn算法 (NIPS, 2013)
熵正则化获取的近似解虽然能够有效降低算法的时间复杂度，但是其潜力还未被充分挖掘。
Sinkhorn算法基于熵正则化的思想，提供一种更加巧妙的求解向量u和v的解法（得到u和v的解，就可以认为得到了Kantorovich Relaxation问题的对偶解，也就是最终的最优解。此处关于其对偶问题的定义和解释，可以参考文献[3]的23页讲解，以及参考资料[11][12]）。具体讲解请见参考资料[13]，部分核心内容如下：
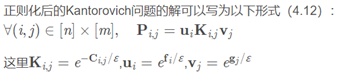
又因为：
结合以上定义，Sinkhorn算法[14]求解u和v的定义公式如下：
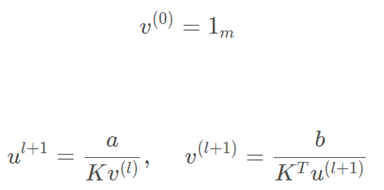
上述公式对应的算法伪码如下[14]：
4 Wasserstein GAN (WGAN) 填补 (ICML, 2017)
此处时一篇2017年的ICML文章，结合了最优运输中的Wasserstein距离来做填补。其填补的核心总结的描述如下[1]，WGAN工作原文请见文献[15]。
5 最优运输填补 (ICML, 2020)
接下来最激动人心的时刻来的，即如何采用最优运输理论进行含缺失数据的填补。原文请见文献[16]。
原文作者提供的代码链接：https://github.com/BorisMuzellec/MissingDataOT
本文工作最大的亮点：采用最优运输的Wasserstein距离、.Entropic 正则化以及Sinkhorn算法理论，笔者认为其实首次将其应用到了含缺失数据的填补，并且填补的性能要优于之前已提出的方法。
本文工作的原理：采用熵正则化和Sinkhorn分歧来计算两个数据分布之间的差异，相关公式如下：
采用最优运输进行填补假设定义：随机从原始的数据集中选取两个bachsize（默认设定为128）大小的数据，该两组数据的分布应该是接近或者理想上是一样的分布。那么，先填补，然采用上述截图中的公式3（Sinkhorn分歧）计算两个大小为bachsize数据分布之间的相似度，如果填补的值越接近实际值，计算的分布相似度值就越优。
依据这样的思想，作者提出了算法1，将填补的值当作反向传播算法待优化更新的参数，采用公式(3)作者损失函数，通过不断迭代更新梯度，不断优化填补的值，使得最终填补的结果越接近实际的真实值。具体的算法伪码如下：
算法1存在一个问题，其填补的值是采用反向传播算法来更新，导致对于新的数据在没有输入到算法1中进行反向传播更新训练时，是无法执行填补的。换句话说，就是一个无参数话的填补算法，不具有模型的迁移学习能力。
针对上述问题，作者提出采用一个线性分类器或者MLP分类器对填补的值进行预测，采用公式（3）作为损失函数，对线性分类器或者MLP分类器的权重参数采用反向传播算法进行更新。最终学习的线性分类器就是一个带参数的填补模型，能够对新的含缺失数据执行填补，文章中也称其为参数化填补算法，具体的算法伪码如下：
上述的算法2是直接对原始数据进行填补，也就是说无论其一条数据中有多少列属性含缺失，都是只执行一次填补，这样会导致无法解耦不同列之间的填补（PS：笔者认为此处提这个原因，可能是直接一次填补的效果不好，不过这个在文章没有进行实验对比分析）。针对上述问题，如果数据集含有n列，则采用n-1列数据对当前的1列数据执行填补，具体的算法伪码如下所示：
然而，笔者通过文章实验结果以及实际实验发现，算法3在时间复杂度上很高。即如果原始数据集的维度很高，那么采用算法3执行填补将会耗费很多时间，导致其实用性不高，对于这个问题原文作者没提。不过对于高维含缺失数据的填补，应该也是属于另外一个研究问题，比如可能需要先执行降维，然后对降维后的数据进行填补。
参考资料
[1] “最优传输之浅谈_Hungryof的专栏-CSDN博客.” https://blog.csdn.net/Hungryof/article/details/110549879 (accessed Mar. 11, 2021).
[2] J. Zhang, W. Zhong, and P. Ma, “A Review on Modern Computational Optimal Transport Methods with Applications in Biomedical Research,” arXiv:2008.02995 [cs, stat], Sep. 2020, Accessed: Mar. 11, 2021. [Online]. Available: http://arxiv.org/abs/2008.02995.
[3] G. Peyré and M. Cuturi, “Computational Optimal Transport,” arXiv:1803.00567 [stat], Mar. 2020, Accessed: Mar. 11, 2021. [Online]. Available: http://arxiv.org/abs/1803.00567.
[4] “最优传输系列-第一篇_Grant Tour of Algorithms-CSDN博客.” https://blog.csdn.net/Utterly_Bonkers/article/details/88387081?utm_medium=distribute.pc_relevant.none-task-blog-baidujs_title-4&spm=1001.2101.3001.4242 (accessed Mar. 11, 2021).
[5] “scipy.stats.wasserstein_distance — SciPy v1.6.1 Reference Guide.” https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.wasserstein_distance.html (accessed Mar. 11, 2021).
[6] “最优传输系列-第二篇_Grant Tour of Algorithms-CSDN博客.” https://blog.csdn.net/Utterly_Bonkers/article/details/88613536?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.control&dist_request_id=1328627.20164.16154281942103719&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.control (accessed Mar. 11, 2021).
[7] “最优传输系列-第四篇（3.1-3.2）_Grant Tour of Algorithms-CSDN博客.” https://blog.csdn.net/Utterly_Bonkers/article/details/88758099?spm=1001.2014.3001.5501 (accessed Mar. 12, 2021).
[8] “最优传输系列-第六篇（3.4.2）_Grant Tour of Algorithms-CSDN博客.” https://blog.csdn.net/Utterly_Bonkers/article/details/89009325?spm=1001.2014.3001.5501 (accessed Mar. 12, 2021).
[9] “最优传输系列-第七篇（3.5-3.5.2）_Grant Tour of Algorithms-CSDN博客.” https://blog.csdn.net/Utterly_Bonkers/article/details/89325557?spm=1001.2014.3001.5501 (accessed Mar. 12, 2021).
[10] “最优传输-熵正则化（第八篇）_Grant Tour of Algorithms-CSDN博客.” https://blog.csdn.net/Utterly_Bonkers/article/details/89546491?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.control&dist_request_id=1328627.22339.16154448009187621&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.control (accessed Mar. 11, 2021).
[11] “凸优化中的对偶（Duality in General Programs）_zbwgycm的博客-CSDN博客.” https://blog.csdn.net/zbwgycm/article/details/104752762 (accessed Mar. 11, 2021).
[12] “最优传输系列-第三篇（2.5）_Grant Tour of Algorithms-CSDN博客.” https://blog.csdn.net/Utterly_Bonkers/article/details/88713539?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-2.control&dist_request_id=1328627.20562.16154282276672995&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-2.control (accessed Mar. 12, 2021).
[13] “最优传输-Sinkhorn算法（第九篇）_Grant Tour of Algorithms-CSDN博客_sinkhorn.” https://blog.csdn.net/Utterly_Bonkers/article/details/90746259?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-2.control&dist_request_id=&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-2.control (accessed Mar. 11, 2021).
[14] M. Cuturi, “Sinkhorn Distances: Lightspeed Computation of Optimal Transportation Distances,” arXiv:1306.0895 [stat], Jun. 2013, Accessed: Mar. 11, 2021. [Online]. Available: http://arxiv.org/abs/1306.0895.
[15] M. Arjovsky, S. Chintala, and L. Bottou, “Wasserstein generative adversarial networks,” in Proceedings of the 34th International Conference on Machine Learning - Volume 70, Sydney, NSW, Australia, Aug. 2017, pp. 214–223, Accessed: Mar. 10, 2021. [Online].
[16] B. Muzellec, J. Josse, C. Boyer, and M. Cuturi, “Missing Data Imputation using Optimal Transport,” arXiv:2002.03860 [cs, stat], Jul. 2020, Accessed: Mar. 12, 2021. [Online]. Available: http://arxiv.org/abs/2002.03860.
