LeetCode刷题总结-树篇(中)
本篇接着《LeetCode刷题总结-树篇(上)》,讲解有关树的类型相关考点的习题,本期共收录17道题,1道简单题,10道中等题,6道困难题。
在LeetCode题库中,考察到的不同种类的树有七种,分别是二叉搜索树、平衡二叉树、满二叉树、完全二叉树、线段树、字典树和树状数组。每一种类型的树,有着不同的特性以及对应的考察重点。考察重点可参考下图,下文按照树的类型分别划分了一个目录章节,并给出了对应的经典习题。
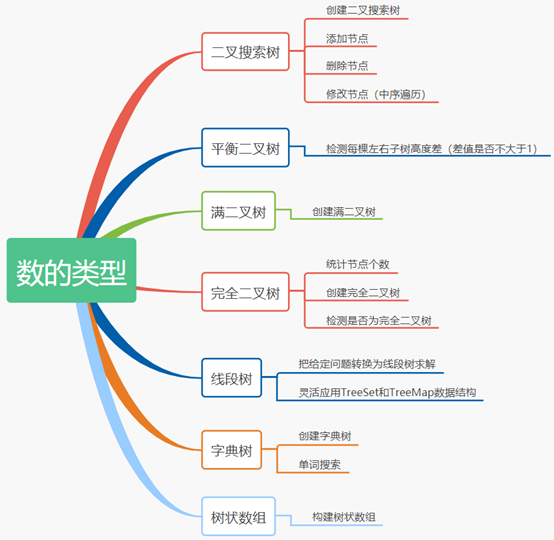
1 二叉树搜索树
基本定义:又称二叉查找树,二叉排序树。若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉搜索树。参考示例图如下(图片来源):

考察重点:二叉搜索树的创建问题、删除二叉树的指定节点、修改二叉树节点的值、添加节点。
由于二搜索树自身的特殊性质,可知插入和查找具体节点的时间复杂度为O(logn)。另外,需要谨记应用中序遍历二叉搜索树得到的序列为升序序列。对于添加、修改二叉树的节点问题,中序遍历的思想一般能够提供较好的解答思路。
本部分收录的习题(下面出现的数字为对应题目在LeetCode题库中的序号),具体如下:
95.不同的二叉搜索树 II,难度:中等 (考察搜索二叉树的创建问题)
99.恢复二叉搜索树,难度:困难 (考察搜索二叉树修改节点的问题)
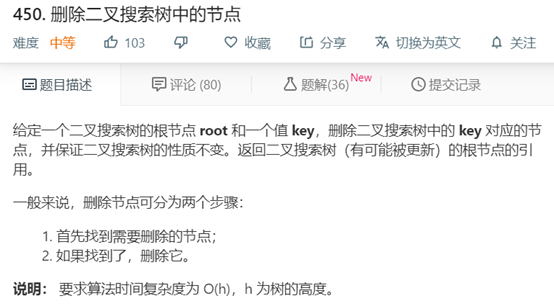
450.删除二叉搜索树中的节点,难度:中等(考察搜索二叉树节点删除问题)
701.二叉搜索树中的插入,难度:中等(考察搜索二叉树节点的插入问题)
对于上述四类考点,应用Java实现删除二叉搜索树中节点时,由于采用递归的解法,需要特别注意深拷贝和浅拷贝的问题。另外,对于删除操作可以采用地址覆盖的操作来实现,此部分的操作代码可以作为模板记住。下面具体给出题号为450题目的描述及解答代码。
题目描述:
解答代码:
class Solution { public TreeNode deleteNode(TreeNode root, int key) { if (root == null) return null; if (key < root.val) { // 待删除节点在左子树中 root.left = deleteNode(root.left, key); return root; } else if (key > root.val) { // 待删除节点在右子树中 root.right = deleteNode(root.right, key); return root; } else { // key == root.val,root 为待删除节点 if (root.left == null) // 返回右子树作为新的根 return root.right; else if (root.right == null) // 返回左子树作为新的根 return root.left; else { // 左右子树都存在,返回后继节点(右子树最左叶子)作为新的根 TreeNode successor = min(root.right); successor.right = deleteMin(root.right); successor.left = root.left; return successor; } } } private TreeNode min(TreeNode node) { if (node.left == null) return node; return min(node.left); } private TreeNode deleteMin(TreeNode node) { if (node.left == null) return node.right; node.left = deleteMin(node.left); return node; } }
2 平衡二叉树
基本定义:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。参考示例图如下(图片来源)
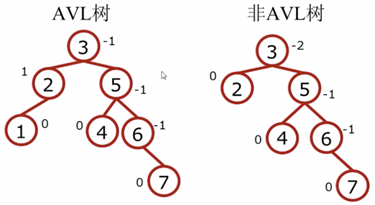
考察重点:给定一棵二叉树,检测该树是否为平衡二叉树。即考察我们递归遍历树的每个节点,检测每个节点对应的左右子树的高度差是否不大于1。
本部分收录的习题:
3 满二叉树
基本定义:每个结点恰好有 0 或 2 个子结点。
考察重点:给定若干个元素,求能够组成的不同满二叉树的个数。
本部分收录的习题:
4 完全二叉树
基本定义:完全二叉树从根结点到倒数第二层满足完美二叉树,最后一层可以不完全填充,其叶子结点都靠左对齐。(附完美二叉树定义:一个深度为k(>=-1)且有2^(k+1) - 1个结点的二叉树称为完美二叉树。)参考示例图如下(图片来源):

考察重点:统计给定树的节点个数、创建完全二叉树以及检测给定树是否为完成二叉树。
本部分收录的习题:
222.完全二叉树的节点个数,难度:中等(考察统计节点个数)
919.完全二叉树插入器,难度:中等(考察创建完全二叉树)
958.二叉树的完全性检验,难度:中等(考察检测是否为完全二叉树)
5 线段树
基本定义:线段树是一种二叉搜索树,与区间树相似,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。参考示例图如下(图片来源):
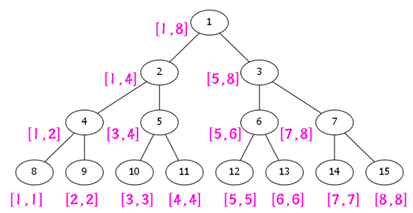
实际应用:使用线段树可以快速的查找某一个节点在若干条线段中出现的次数,时间复杂度为O(logN)。
考察重点:给定问题,灵活转换为线段树求解。
应用Java语言创建线段树时,可以借助内置的TreeSet和TreeMap数据结构。TreeSet是HashSet的升级版,TreeMap则是HashMap的升级版
本部分收录的习题:
715. Range模块,难度:困难(可以采用TreeSet构建线段树,需要熟悉TreeSet在Java中相关接口的用法)
732.我的日程安排表III ,难度:困难 (可以采用TreeMap构建模拟化线段树,需要熟悉TreeMap在Java中相关接口的用法)
850.矩形面积II,难度:困难(考察定义线段树的标准解法)
6 字典树
基本定义(百度百科):又称单词查找树、前缀树、Trie树,是一种树形结构,是一种哈希树的变种。典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,查询效率比哈希树高。参考示例图如下(图片来源):
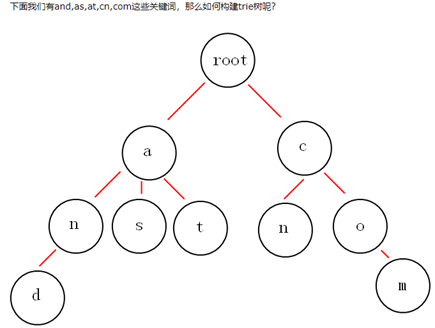
考察重点:创建字典树、单词搜索。
本部分收录的习题:
208.实现Trie(前缀树),难度:中等(考察创建字典树)
212.单词搜索II,难度:困难(考察单词搜索)
648.单词替换,难度:中等(考察单词搜索)
7 树状数组
基本定义(百度百科):是一个查询和修改复杂度都为log(n)的数据结构。主要用于查询任意两位之间的所有元素之和,但是每次只能修改一个元素的值;经过简单修改可以在log(n)的复杂度下进行范围修改,但是这时只能查询其中一个元素的值(如果加入多个辅助数组则可以实现区间修改与区间查询)。参考示例图如下(图片来源):
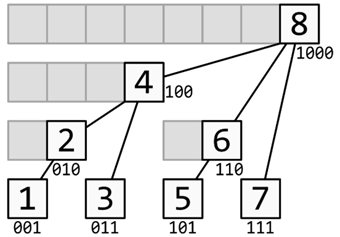
考察重点:构建树状数组。
本部分收录的习题:

 浙公网安备 33010602011771号
浙公网安备 33010602011771号