Stack栈详解 图解 引入到LinkedList和Array实现、均摊时间分析| Stack ADT details, intro to implementation and amortized time analysis with figures.
Stack ADT(abstract data type)
Introduction of Stack
Normally, mathematics is written using what we call in-fix notation:
Any operator is placed between two operands. The advantage is that it's intuitive enough for human, the disadvantage is obvious. When the mathematics formula is too long, it's full of parentheses and is difficult to find where to start calculation, both for people and computers.
Alternatively, we can place the operands first, followed by the operator.
Parsing reads left-to-right and performs any operands on the last two operands.
This is called Reverse-Polish notation after the mathematician Jan Łukasiewicz.
Its advantage is that no ambiguity and no brackets are needed. And it's the same process used by a computer to perform computations:
operands must be loaded into register before operations can be performed on them
The easiest way to parse reverse-Polish notation is to use an operand stack. So what is a stack?
What is a stack?
Stack is a last-in-first-out(LIFO) data structure. It's like a pile of plates. Every time you take the plate, you take the top. After washing the plate, you also put the plate on the top.
Deal with Reverse-Polish Notation
Operands are proceeded by pushing them onto the stack.
When processing an operator:
- pop the last two items off the operand stack
- perform the operation, and
- push the result back onto the stack
Example: how do we evaluate 1 2 3 + 4 5 6 × - 7 × + - 8 9 × - using a stack:

Implementation of Stack
We have 5 main operation of stack, they are:
Push: insert an object onto the top of stackPop: erase the object on the top of the stackIsEmpty: determine if the stack is emptyIsFull: determine if a stack is fullCreateStack: generate an empty stack
We expect the optimal asymptotic run time of above operations is \(\Theta(1)\), which means that the run time of this algorithm is independent of the number of objects being stored in the container.
Linked-List Implementation
Operations at the front of a single linked list are all \(\Theta(1)\).

The desired behavior of an Abstract Stack may be reproduced by performing all operations at the front.
push_front(int)
void List::push_front(int n){
list_head = new Node(n, list_head)
}
pop_front()
int List::pop_front(){
if( empty() ){
throw underflow();
}
int e = front();
Node *ptr = list_head;
list_head = list_head->next();
delete ptr;
return e;
}

Array Implementation
For one-ended arrays, all operations at the back are \(\Theta(1)\). But the insert at the front or pop at front takes \(\Theta(n)\) to move all element one place backwards.
top()
If there are \(n\) objects in the stack, the last is located at index \(n-1\).
template <typename Type>
T Stack<T>::top() const{
if( empty() ){
throw underflow();
}
return array[stack_size-1];
}
pop()
Remove an object simply involves reducing the size. After decreasing the size, the previous top of the stack is now at the location stack_size.
template <typename Type>
T Stack<T>::pop() const{
if( empty() ){
throw underflow();
}
stack_size--;
return array[stack_size];
}
push(obj)
Pushing an object can only be performed if the array is not full
template <typename Type>
void Stack<T>::push(T const &obj) const{
if( stack_size == array_capacity ){
throw overflow();
}
array[stack_size] = obj;
stack_size++;
}
Array Capacity
When the array is full, how to increase the array capacity?
So the question is:
How must space will be increased? By a constant or a multiple?
First, let see how an increase works.
Firstly, require a call to new memory: new T[N] where N is the new capacity.
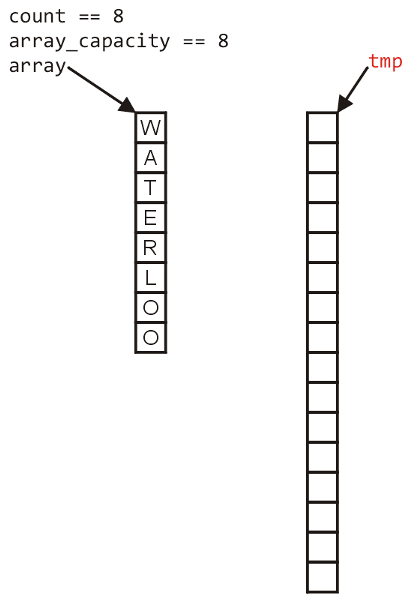
Next, copy old data to new space:
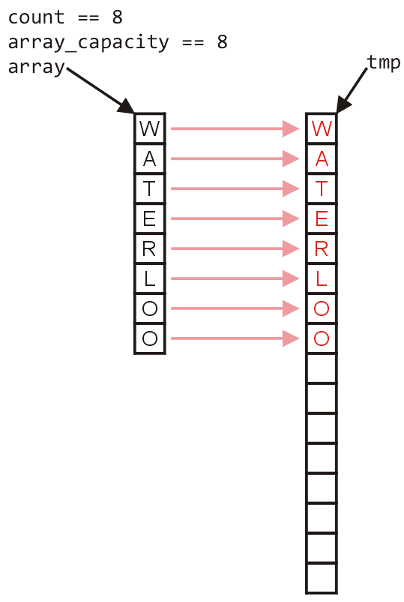
The memory for original array must be deallocated:
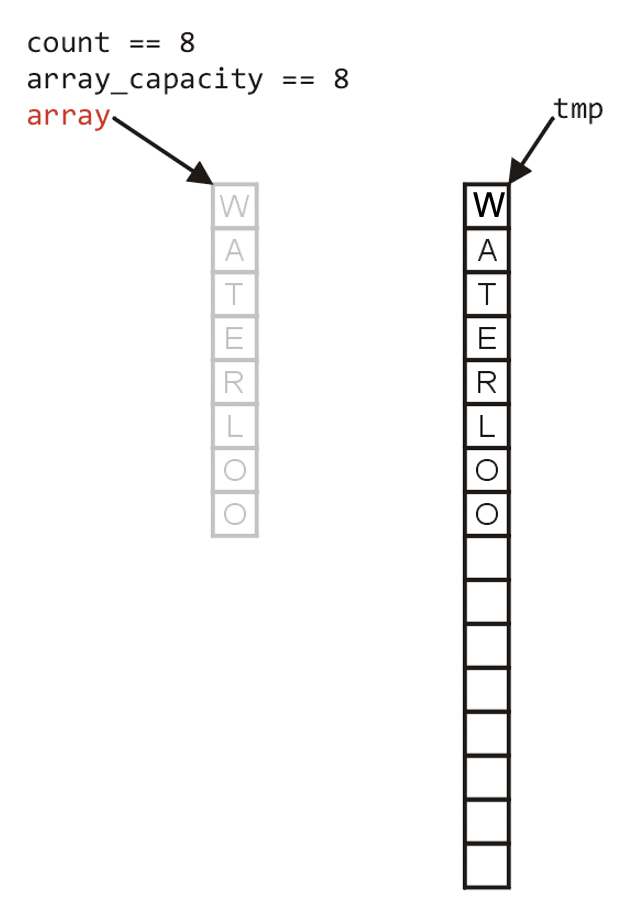
Finally, the pointer should point to new memory address:
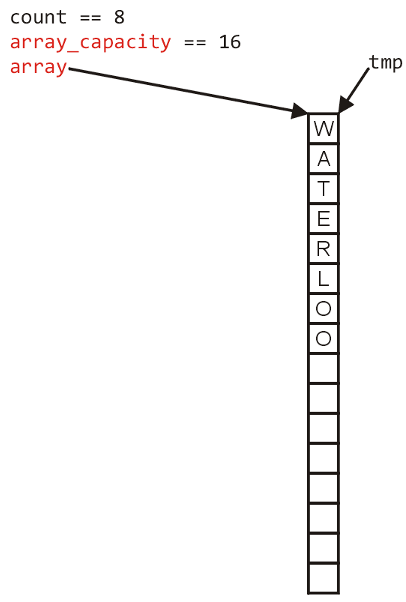
Now, back to the original question: How much do we change the capacity?
We recognize that any time we push onto a full stack, this requires \(n\) copies and the run time is \(\Theta(n)\). Therefore, push is usually \(\Theta(1)\) except when new memory is required.
To state the average run time, we introduce the concept of amortized time:
If
noperations requires \(\Theta(f(n))\), we will say that an individual operation has an amortized run time of \(\Theta(f(n)/n)\).
Using this concept, if inserting n objects requires:
- \(\Theta(n^2)\) copies, the amortized time is \(\Theta(n)\)
- \(\Theta(n)\) copies, the amortized time is \(\Theta(1)\), that is what we expect.
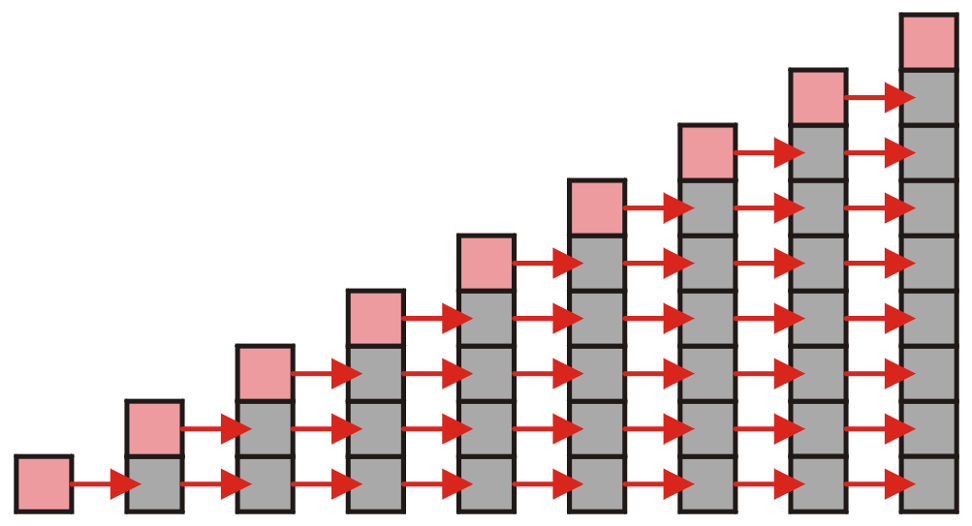
Capacity increase 1 analysis
If we increase the capacity by 1 each time the array is full. With each insertion when the array is full, its requires all entries to be copied.
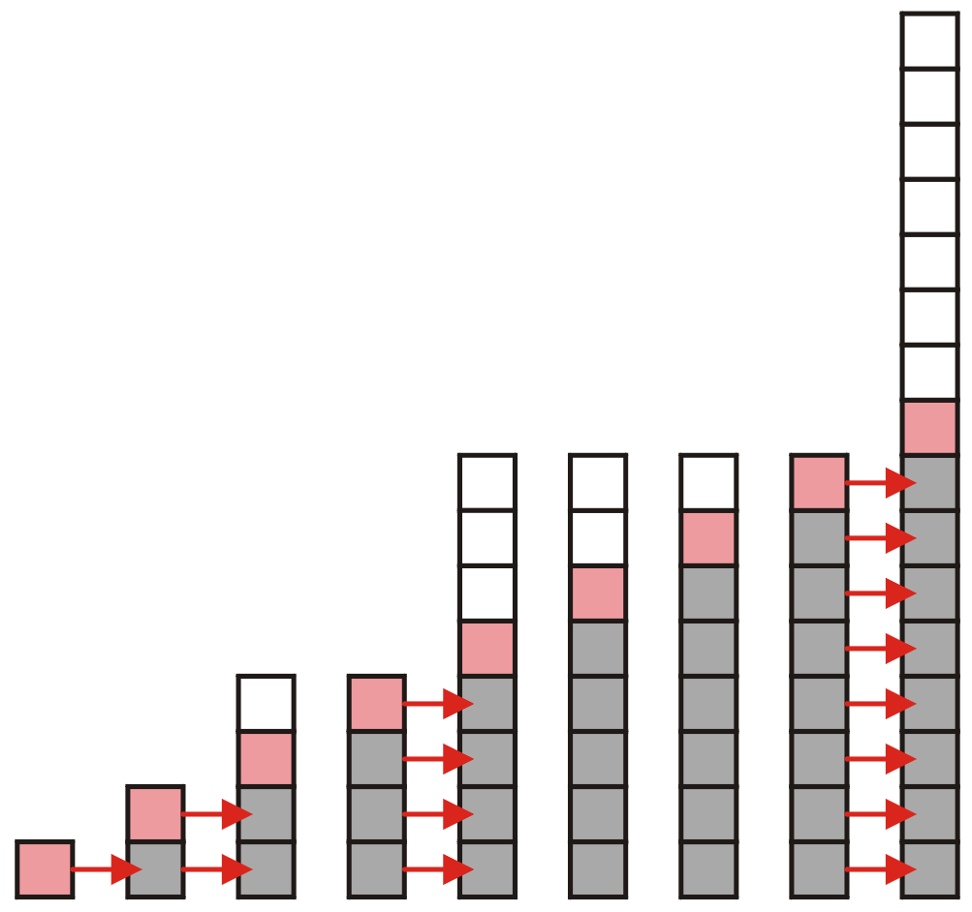
Capacity become double size analysis
Suppose we double the number of entries each time the array is full.
Now the copy time become significantly fewer.
Example Applications
Most parsing uses stacks.
Examples includes:
- Matching tags in XHTML
- In C++, matching parentheses \(\textbf{(...)}\), brackets \(\textbf{[...]}\) and braces \(\textbf{\{...\}}\)
Resources: ShanghaiTech 2020Fall CS101 Algorithm and Data Structure.



 浙公网安备 33010602011771号
浙公网安备 33010602011771号