并查集详解 图解引入到实现｜ Disjoint Sets details, intro to implementation with figures.

Introduction of Disjoint Sets

It's easy to tell whether someone you know is your relative. He or she may be your uncle, grandparent or nephew. Because your blood relationship is within two or three generations. Consider such a scenario, you meet someone on street in your town. How to judge if you are relatives, even distant kinship?
It's hard to remember all members of you family. But it's easy to remember a specific person, who is your ancestor. So everyone just need to remember who is his or her ancestor. When meet a new person, by comparing whether your ancestors were the same person, you can know whether you are relatives or not. If your ancestors are different, then you are not in a same family.
Now, consider a new scenario. Two family are very close, such that they want to merge into a big family(through marriage, etc.). After merger, in order to handle the upper scenario easily, they choose someone to be the new "ancestor" and everyone in the two family remembers this person, now they become a bigger family.

The main concept of recognizing relatives is that using a person in the family(ancestor) to representative this family. When merging two family, update everyone's remembered ancestor to the new ancestor.

We can abstract above scenario as: Using one element in the set to represent the set. Update the representative element when merging two or more sets. That is Disjoint Sets.

Operations on Disjoint Sets

There are mainly 2 operations on disjoint sets:

• find: find out which set I am in.
• set_union: merge two sets.

find

Objective: Determine if two elements are in the same disjoint set.

We will determine if two objects are in the same disjoint set by defining a find function.

• find(a): find the representative object of the disjoint set that a belongs to.
• Given two elements a and b, they are in the same set if find(a)=find(b).

We use an array to store each elements' representative object.

e.g. In the diagram above, we can tell 2,6,10,14,18,22 are in the same set, and their representative element is 2.

We can abstract the array into a tree structure as follows:

e.g. In the diagram above, 6,10,14,18,22's parent is 2, so they are in the same family.

Since each element only cares the one in root; therefore, each element store it's parent(point to its parent in tree structure). As follows:

implementation of find

Assume we are creating disjoint sets for the n integers.

0, 1, 2, ..., n-1

Define a array: parent = new int[n]
If parent[i]==i, then i is a root node.
Initialization: each integer is in its own set

for ( int i = 0; i < n; i++) {
	parent[i] = i;
}

like following:

Now we can implement find(long i) as follows:

public long find(long i){
	while( parent[i] != i){
		i = parent[i];
	}
	return i;
}

The time for find(long i) is \(T_{find}(n)=O(h)\), where \(h\) is the height of the abstract tree.

set_union

Objective: Take the union of two disjoint sets to create a new single set.

implementation of set_union

To union two set, we just need to attach one set's representative number to the other set's parent:

public void set_union(long i, long j){
	i = find(i);
	j = find(j);
	parent[j] = i;
}

The time for set_union(long i, long j) is \(T_{set_union}=2T_{find}(n)+\Theta(1)=O(h)\).

Optimization

Minimize the height of the tree

In the find and set_union above, \(T=O(h)\), where \(h\) is the height of the tree. When we do union operation, the height of tree increases and the time for find and set_union increases.

Worst-Case Scenario

Let us consider creating the worst-case disjoint set. That is the tallest tree with the least number of nodes.
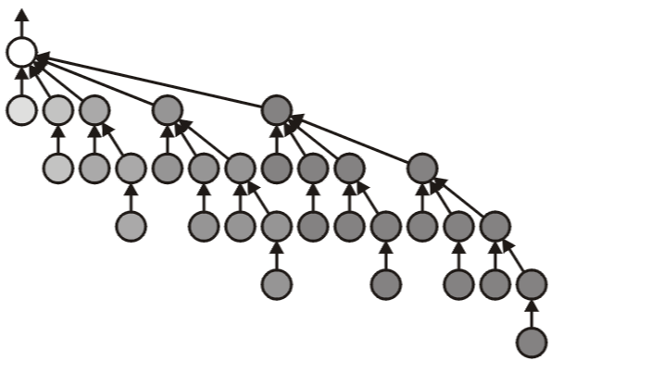
The worst case tree of height \(h\) must results from taking union of two worst case trees of height \(h-1\). As shown in the following figures.

From the construction, the number of nodes in each layer form Pascal's triangle.
Suppose the worst-case tree of height \(h\).

• The number of node is: \(\sum_{k=0}^{h}\left(\begin{array}{l}h\\ k\end{array}\right)=2^{h}=n\)
• The sum of node depth is: \(\sum_{k=0}^{h} k\left(\begin{array}{l}h \\ k\end{array}\right)=h 2^{h-1}\)
• Thus, the average depth is: \(\frac{h 2^{h-1}}{2^{h}}=\frac{h}{2}=\frac{\lg (n)}{2}\)
• The height and average depth of the worst case are \(O(\ln(n))\).

Best-Case Scenario

In the best case, all element point to the same entry with a resulting height of \(\Theta(1)\):

Path Compression

Once we call find(long a) function, we can find the presentative element of a, why not just point a to its presentative element? So that at next call, our find(a) is \(\Theta(1)\).
Whenever find is called, update the object to point to the root.

public long find(long i){
	if (parent[i] == i){
		return i;
	} else {
		parent[i] = find(parent[i]);
		return parent[i];
	}
}

The next call to find(i) is \(\Theta(1)\). The cost of memory is \(O(h)\).

e.g. find(e)

We call find(e), and in the find function we will do find operation for all node on the path from e to root node c: b and a. So after find(e), a,b,e all point to root node c directly.

---

Resources: ShanghaiTech 2020Fall CS101 Algorithm and Data Structure.