最优二叉树(赫夫曼树)

赫夫曼树的介绍(写的不好地方大佬请指教)

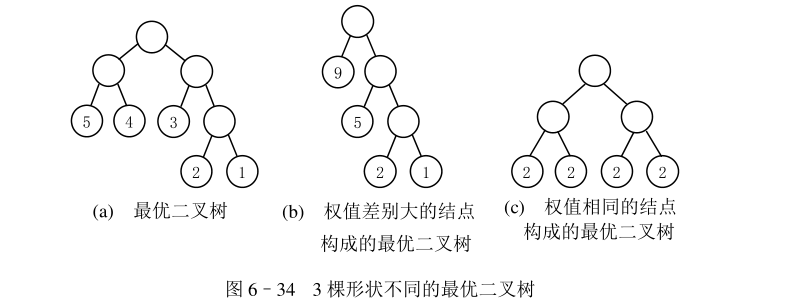
最优二叉树又称哈夫曼树，是带权路径最短的二叉树。根据节点的个数，权值的不同，最优二叉树的形状也不同。

图 6-34 是 3 棵最优二叉树的例子，它们共同的特点是带权节点都是叶子节点，权值越小，就离根节点也远，那么我们是如何构建这颗最优二叉树

步骤如下：

那如何创建这一个哈夫曼树呢？(百度百科)

假设有n个权值，则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn，则哈夫曼树的构造规则为：

(1) 将w1、w2、…，wn看成是有n 棵树的森林(每棵树仅有一个结点)；

(2) 在森林中选出两个根结点的权值最小的树合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和；

(3)从森林中删除选取的两棵树，并将新树加入森林；

(4)重复(2)、(3)步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。

如：对下图中的六个带权叶子结点来构造一棵哈夫曼树，步骤如下：

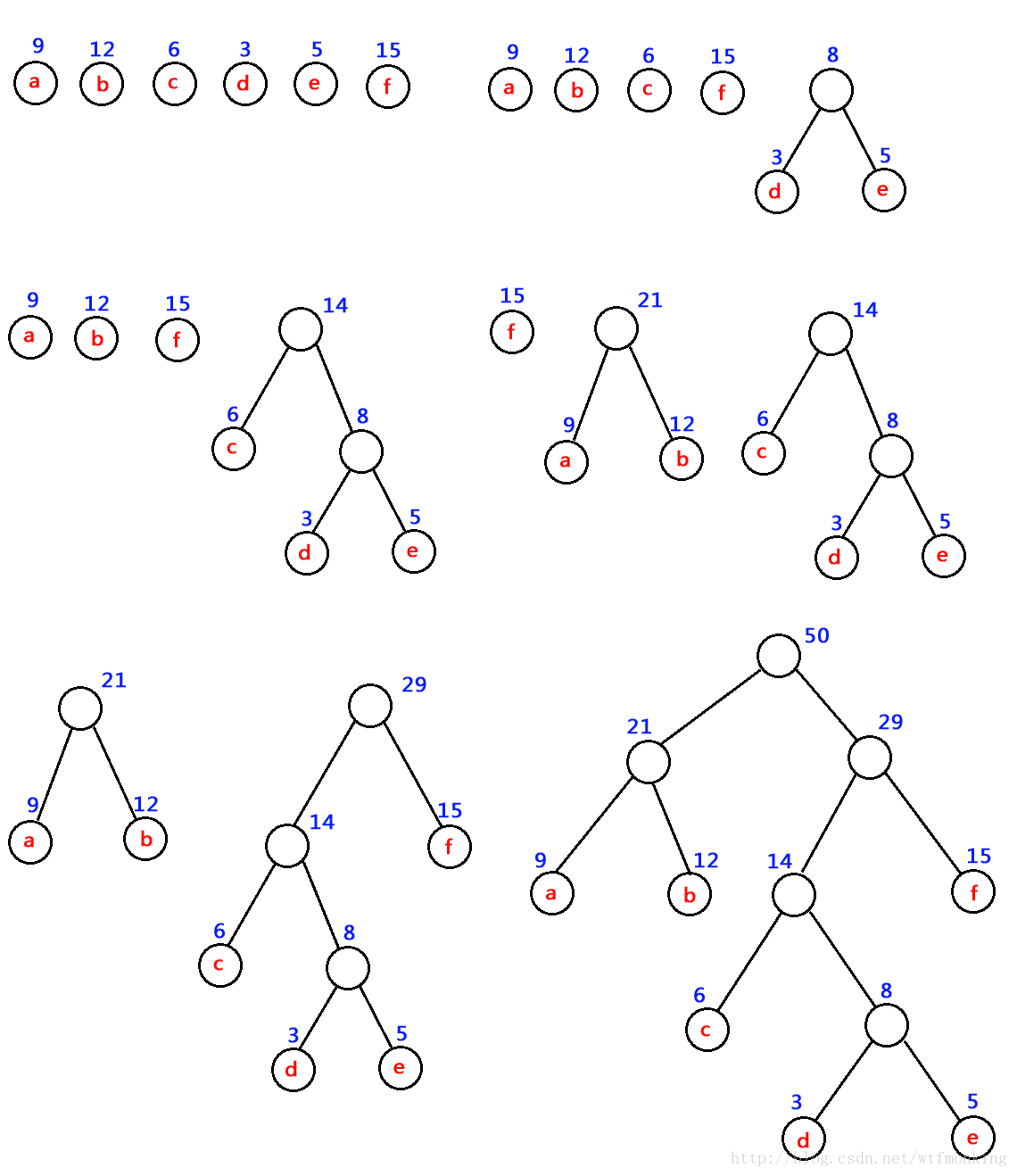
当建立好哈夫曼树，我们要将其进行编码，要将权值表示改为0,1表示，叶子节点的左边改为0，右边改为1

这样子比较方便在网络上传输，因为哈夫曼树的研究目的就是为了解决早期远距离通信(电报)的数据传输的优化问题。

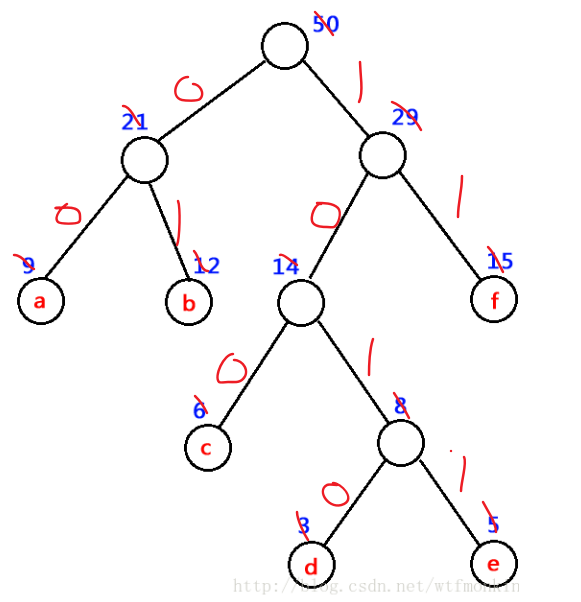
接下来我们来分析一下，这样做对数据的优化体现在哪里？

例如，如上图。6-12-9，

假如们要传输一端报文：BADCADFEED,那么我们可以用相应的二进制表示

字母	a	b	c	d	e	f
二进制字符	000	001	010	011	100	101

这样真正的传输的数据编码二进制后就是：001000011010000011101100100011（共30个字符），可见如果传输数据过大，这个报文的编码也就越大了。

但是如果我们按照上面的哈夫曼树进行编码的话

字母	a	b	c	d	e	f
二进制字符	01	1001	101	00	11	1000

新编码后的数据是：1001010010101001000111100(共25个字符)

大约节约了17%的存储或传输文本，随着字符的增加和多字符权重的不同，这种压缩会更加突显出来优势。

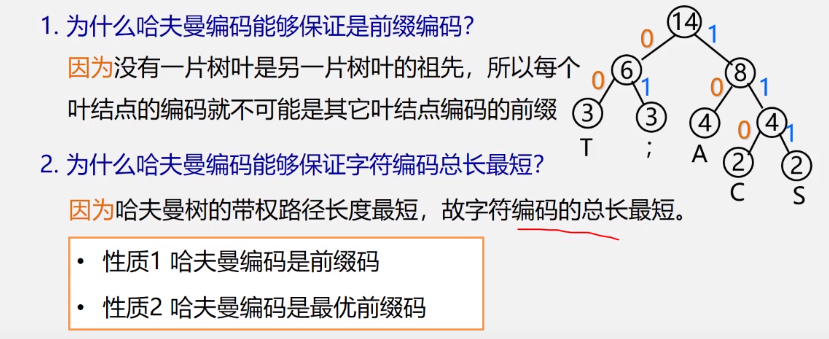
0和1是比较容易混淆的，为了设计出来长度不相等的编码，我们就必须有一种规定，就是任一字符的编码都不是另一个字符的编码的前缀，这种编码被称为前缀编码。

我们可以发现通过哈夫曼编码形成的每个节点的编码例如：1000,1000混淆的10,100的类似的编码了。

当接收者收到了这个已经经过编码的二进制数后，我们要如何进行解码，才能看到发送者真正想发给接收者的消息呢？

解码的时候，必须用到双方约定好的哈夫曼树：

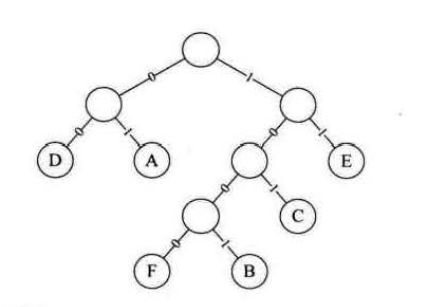
从根节点开始遍历，就可以知道A是01，E是11,B是 1001 ，其余的节点信息也可以相应的得到，从而成功解码。

哈夫曼树的节点存储结构

1 //哈夫曼树结构
2 ; typedef struct{
3     unsigned int weight;          //权重
4     unsigned int parent, lchild, rchild;  //树的双亲节点，和左右孩子
5 
6 }HTNode, *HuffmanTree;
7 
8 typedef char**  HuffmanCode;

基本思路就是：

1、首先我们要建立一个哈夫曼树。

2、这个哈夫曼树有的特点在上面有介绍。

3、对哈夫曼树进行0,1编码

4，最后打印出已经编码完成的哈夫曼树。

里面最难的两部步应该是建树，解码输出(可能我比较笨把，搞了二天才搞明白)

1、建树，根据节点的权重建立，每次从的序列中比较出两个最小的权重，建立出一颗树，然后再从剩余的节点中继续抽取节点权重最小的节点，继续建树，这边我采用的是迭代方式；

2、解码输出，采用的是叶子节点逆序遍历到根节点，将0,1存储到字符数组里面，然后再将数组输出。

里面是具体实现的代码，里面也有注释

1 //函数声明
2 int Min(HuffmanTree T, int i); //求i个节点中的最小权重的序列号，并返回
3 void Select(HuffmanTree T, int i, int& s1, int& s2); //从两个最小权重中选取最小的(左边)给s1，右边的给s2
4 void HuffmanCoding(HuffmanTree &HT, HuffmanCode&HC, int* w, int n);//哈夫曼编码与解码

函数的具体实现算法1：

 1 //返回i个节点中权值最小的树的根节点的序号，供select()调用
 2 int Min(HuffmanTree T, int i){
 3     int j, flag;
 4     unsigned int k = UINT_MAX;  //%d-->UINT_MAX = -1,%u--->非常大的数
 5     for (j = 1; j <= i; j++)
 6         if (T[j].weight < k && T[j].parent == 0)
 7             k = T[j].weight, flag = j;                  //
 8     T[flag].parent = 1;    //将parent标志为1避免二次查找
 9 
10     return flag;   //返回节点的下标
11 }
12 
13 void Select(HuffmanTree T, int i,int& s1,int& s2){
14     //在i个节点中选取2个权值最小的树的根节点序号，s1为序号较小的那个
15     int j;
16     s1 = Min(T,i);
17     s2 = Min(T,i);
18     if (s1 > s2){
19         j = s1;
20         s1 = s2;
21         s2 = j;
22     }
23 }

解码算法1(从根节点遍历赫夫曼树逆序输出)：

 1 //HuffmanCode代表的树解码二进制值
 2 void HuffmanCoding(HuffmanTree &HT, HuffmanCode&HC, int* w, int n){
 3     //w存放n个字符的权值(均>0),构造哈夫曼树HT,并求出n个字符的哈夫曼编码HC
 4     int m, i, s1, s2, start;
 5     unsigned c, f;
 6     char* cd;
 7     //分配存储空间
 8     HuffmanTree p;
 9     if (n <= 1)
10         return;
11     //n个字符(叶子节点)有2n-1个树节点，所以树节点m
12     m = 2 * n - 1;
13     HT = (HuffmanTree)malloc((m + 1)*sizeof(HTNode));  //0号元素未用
14     //这一步是给哈夫曼树的叶子节点初始化
15     for (p = HT + 1, i = 1; i <= n; ++i, ++p, ++w)
16     {
17         (*p).weight = *w;
18         (*p).lchild = 0;
19         (*p).rchild = 0;
20         (*p).parent = 0;
21     }
22     //这一步是给哈夫曼树的非叶子节点初始化
23     for (; i <= m; ++i, ++p){
24         (*p).parent = 0;
25     }
26     /************************************************************************/
27     /* 做完准备工作后 ，开始建立哈夫曼树
28     /************************************************************************/
29     for (i = n + 1; i <= m; i++)
30     {
31         //在HT[1~i-1]中选择parent=0且weigh最小的节点，其序号分别为s1,s2
32         Select(HT, i - 1, s1, s2);  //传引用
33         HT[s1].parent = HT[s2].parent = i;
34         HT[i].lchild = s1;
35         HT[i].rchild = s2;
36         HT[i].weight = HT[s1].weight + HT[s2].weight;
37     }
38     /************************************************************************/
39     /* 从叶子到根逆求每个叶子节点的哈夫曼编码                                          */
40     /************************************************************************/
41     //分配n个字符编码的头指针向量，（[0]不用）
42     HC = (HuffmanCode)malloc((n + 1)*sizeof(char*));
43     cd = (char*)malloc(n*sizeof(char));   //分配求编码的工作空间
44     cd[n - 1] = '\0'; //结束符
45     for (i = 1; i <= n; i++)  //每个节点的遍历
46     {
47         start = n - 1; c = i; f = HT[i].parent; //c表示当前节点的下标
48         while (f != 0){       //父节点不为0，即不为根节点
49             --start;
50             if (HT[i].lchild == c)cd[start] = '0';
51             else
52                 cd[start] = '1';
53             c = f; f = HT[f].parent;  //迭代向上回溯
54         }
55         HC[i] = (char*)malloc((n - start)*sizeof(char));  //生成一个块内存存储字符
56         //为第i个字符编码分配空间
57         strcpy(HC[i], &cd[start]);  //从cd赋值字符串到cd
58     }
59     free(cd);  //释放资源
60 }

这里面有一个地方钻牛角尖了，卡了一段时间，那就是我们输入的权重是存储在w这块内存里面的，并通过权重建立起来的树，于是HT内存存储的第一个节点也就是我们输入权重所对应的第一个节点。于是我们开始逆序输出解码时，所对应的每个节点的解码与权重所对应的一一对应。

解码算法2(从根节点正序遍历赫夫曼树输出)：

 1 //利用无栈递归的思想
 2 void HuffmanCoding2(HuffmanTree &HT, HuffmanCode &HC, int* weight, int n){
 3     int m, i, s1, s2;
 4     unsigned c, cdlen;
 5     HuffmanTree p;
 6     char* cd;  //编码空间
 7 
 8     if (n <= 1)
 9         return;
10     m = 2 * n - 1;
11     HT = (HuffmanTree)malloc((m + 1)*sizeof(HTNode)); //1开始到m+1//总共2n-1
12     for (p = HT + 1, i = 1; i <= n; ++i, ++weight, ++p){
13 //         HT[i].weight = *weight;
14 //         HT[i].parent = 0;
15 //         HT[i].lchild = 0;
16 //         HT[i].rchild = 0;
17         (*p).weight = *weight;
18         (*p).parent = 0;
19         (*p).lchild = 0;
20         (*p).rchild = 0; 
21     }
22     for (; i <= m; ++i,++p)
23         (*p).parent = 0;
24     /************************************************************************/
25     /* 将树的叶子节点和即将存储的双亲节点初始化后，开始建立赫夫曼树                                                                     */
26     /************************************************************************/
27 
28     for (i = n + 1; i <= m; ++i)  //i++ --->++i
29     {
30         Select(HT, i - 1, s1, s2);
31         HT[s1].parent = HT[s2].parent=i;
32         HT[i].lchild = s1;
33         HT[i].rchild = s2;
34         HT[i].weight = HT[s1].weight + HT[s2].weight;
35     }
36 
37     c = m;  //c = 2*n-1
38     HC = (HuffmanCode)malloc((n + 1)*sizeof(char*));
39     cd = (char*)malloc(n*sizeof(char));
40     cdlen = 0;
41     for (i = 1; i <= m; i++)
42         HT[i].weight = 0;              //将所有的权重置0
43 
44     //这是一个迭代的过程
45     while (c){
46         if (HT[c].weight == 0){
47             //向左
48             HT[c].weight = 1;
49             if (HT[c].lchild != 0){
50                 c = HT[c].lchild;
51                 cd[cdlen++] = '0';
52             }
53             else if (HT[c].rchild == 0)
54             {
55                 cd[cdlen] = '\0';
56                 HC[c] = (char*)malloc(sizeof(char)*(cdlen + 1));
57                 strcpy(HC[c], cd);  //复制编码串            
58             }
59         }
60         else if (HT[c].weight == 1)
61         {
62             //向右遍历
63             HT[c].weight = 2;
64             if (HT[c].rchild != 0){ //存在右孩子
65                 c = HT[c].rchild;
66                 cd[cdlen++] = '1';
67             }
68         }
69         else{   //当HT[c].weight = 2;
70             HT[c].weight = 0;
71             c = HT[c].parent;  //退回到父节点
72             cdlen--;  //编码的长度-1
73         }
74     }
75 }

主函数具体实现：

 1 int main(){
 2 
 3     HuffmanTree HT;
 4     HuffmanCode HC;
 5     
 6     int *w, n, i;
 7     printf("请输入权值的个数(>1):");
 8     scanf_s("%d",&n);
 9 
10     w = (int*)malloc(n*sizeof(int));
11     printf("请依次输入%d个权值(整形):\n",n);
12 
13     for (i = 0; i <= n - 1;i++)
14     {
15         scanf_s("%d",w+i);
16     }
17      HuffmanCoding(HT, HC, w, n);
18 　　　　
19     for (i = 1; i <= n;i++)
20     {
21         puts(HC[i]);
22     }
23     return 0;
24 }

全部代码实现

  1 #include<string.h>
  2 #include<malloc.h>  //malloc()等
  3 #include<stdio.h>
  4 #include<stdlib.h>
  5 #include<ctype.h>
  6 #include<limits.h>
  7 #include<iostream>
  8 
  9 #define TRUE 1
 10 #define FALSE 1
 11 #define OK 1
 12 #define ERROR 1
 13 #define INFEASIBLE -1
 14 
 15 typedef int Status;
 16 typedef int Boolean；
 17 /************************************************************************/
 18 /* 最优二叉树简称：哈夫曼树                                                                     */
 19 /************************************************************************/
 20 //哈夫曼树结构
 21 ; typedef struct{
 22     unsigned int weight;          //权重
 23     unsigned int parent, lchild, rchild;  //树的双亲节点，和左右孩子
 24 
 25 }HTNode, *HuffmanTree;
 26 
 27 typedef char**  HuffmanCode;
 28 
 29 
 30 //返回i个节点中权值最小的树的根节点的序号，供select()调用
 31 int Min(HuffmanTree T, int i){
 32     int j, flag;
 33     unsigned int k = UINT_MAX;  //%d-->UINT_MAX = -1,%u--->非常大的数
 34     for (j = 1; j <= i; j++)
 35         if (T[j].weight < k && T[j].parent == 0)
 36             k = T[j].weight, flag = j;                  //
 37     T[flag].parent = 1;    //将parent标志为1避免二次查找
 38 
 39     return flag;   //返回
 40 }
 41 
 42 void Select(HuffmanTree T, int i,int& s1,int& s2){
 43     //在i个节点中选取2个权值最小的树的根节点序号，s1为序号较小的那个
 44     int j;
 45     s1 = Min(T,i);
 46     s2 = Min(T,i);
 47     if (s1 > s2){
 48         j = s1;
 49         s1 = s2;
 50         s2 = j;
 51     }
 52 }
 53 
 54 //HuffmanCode代表的树解码二进制值
 55 void HuffmanCoding(HuffmanTree &HT, HuffmanCode&HC, int* w, int n){
 56     //w存放n个字符的权值(均>0),构造哈夫曼树HT,并求出n个字符的哈夫曼编码HC
 57     int m, i, s1, s2, start;
 58     unsigned c, f;
 59     char* cd;   
 60     //分配存储空间
 61     HuffmanTree p;
 62     if (n <=1)
 63         return;
 64     //n个字符(叶子节点)有2n-1个树节点，所以树节点m
 65     m = 2 * n - 1;
 66     HT = (HuffmanTree)malloc((m + 1)*sizeof(HTNode));  //0号元素未用
 67     //这一步是给哈夫曼树的叶子节点初始化
 68     for (p = HT + 1, i = 1; i <= n; ++i, ++p,++w)
 69     {
 70         (*p).weight = *w;
 71         (*p).lchild = 0;
 72         (*p).rchild = 0;
 73         (*p).parent = 0;
 74     }
 75     //这一步是给哈夫曼树的非叶子节点初始化
 76     for (; i <= m; ++i, ++p){
 77         (*p).parent = 0;
 78     }
 79     /************************************************************************/
 80     /* 做完准备工作后 ，开始建立哈夫曼树                                                               
 81     /************************************************************************/
 82     for (i = n + 1; i <= m; i++)
 83     {
 84         //在HT[1~i-1]中选择parent=0且weigh最小的节点，其序号分别为s1,s2
 85         Select(HT, i - 1, s1, s2);  //传引用
 86         HT[s1].parent = HT[s2].parent= i;
 87         HT[i].lchild = s1;
 88         HT[i].rchild = s2;
 89         HT[i].weight = HT[s1].weight + HT[s2].weight;
 90     }
 91     /************************************************************************/
 92     /* 从叶子到根逆求每个叶子节点的哈夫曼编码                                          */
 93     /************************************************************************/
 94     //分配n个字符编码的头指针向量，（[0]不用）
 95     HC = (HuffmanCode)malloc((n + 1)*sizeof(char*));  
 96     cd = (char*)malloc(n*sizeof(char));   //分配求编码的工作空间
 97     cd[n - 1] = '\0'; //结束符
 98     for (i = 1; i <= n; i++)  //每个节点的遍历
 99     {
100         start = n - 1;
101         for (c = i, f = HT[i].parent; f != 0; c = f,f = HT[f].parent){ //每个节点到根节点的遍历
102             //从叶子节点到根节点的逆序编码
103             if (HT[f].lchild == c)
104                 cd[--start] = '0';
105             else
106                 cd[--start] = '1';
107         }
108         HC[i] = (char*)malloc((n - start)*sizeof(char));  //生成一个块内存存储字符
109         //为第i个字符编码分配空间
110         strcpy(HC[i], &cd[start]);  //从cd赋值字符串到cd
111     }
112     free(cd);  //释放资源
113 }
114 
115 //函数声明
116 int Min(HuffmanTree T, int i); //求i个节点中的最小权重的序列号，并返回
117 void Select(HuffmanTree T, int i, int& s1, int& s2); //从两个最小权重中选取最小的(左边)给s1，右边的给s2
118 void HuffmanCoding(HuffmanTree &HT, HuffmanCode&HC, int* w, int n);//哈夫曼编码与解码
119 
120 int main(){
121 
122     HuffmanTree HT;
123     HuffmanCode HC;
124     
125     int *w, n, i;
126     printf("请输入权值的个数(>1):");
127     scanf_s("%d",&n);
128 
129     w = (int*)malloc(n*sizeof(int));
130     printf("请依次输入%d个权值(整形):\n",n);
131 
132     for (i = 0; i <= n - 1;i++)
133     {
134         scanf_s("%d",w+i);
135     }
136      HuffmanCoding(HT, HC, w, n);
137 
138     for (i = 1; i <= n;i++)
139     {
140         puts(HC[i]);
141     }
142     return 0;
143 }