6、逻辑代数的化简(公式法和卡诺图法)
一、逻辑函数的化简
将一个逻辑表达式变得最简单、运算量最少的形式就叫做化简。由于 运算量越少,实现逻辑关系所需要的门电路就越少,成本越低,可靠性相对较高,因此在设计逻辑电路时,需要求出逻辑函数的最简表达式。
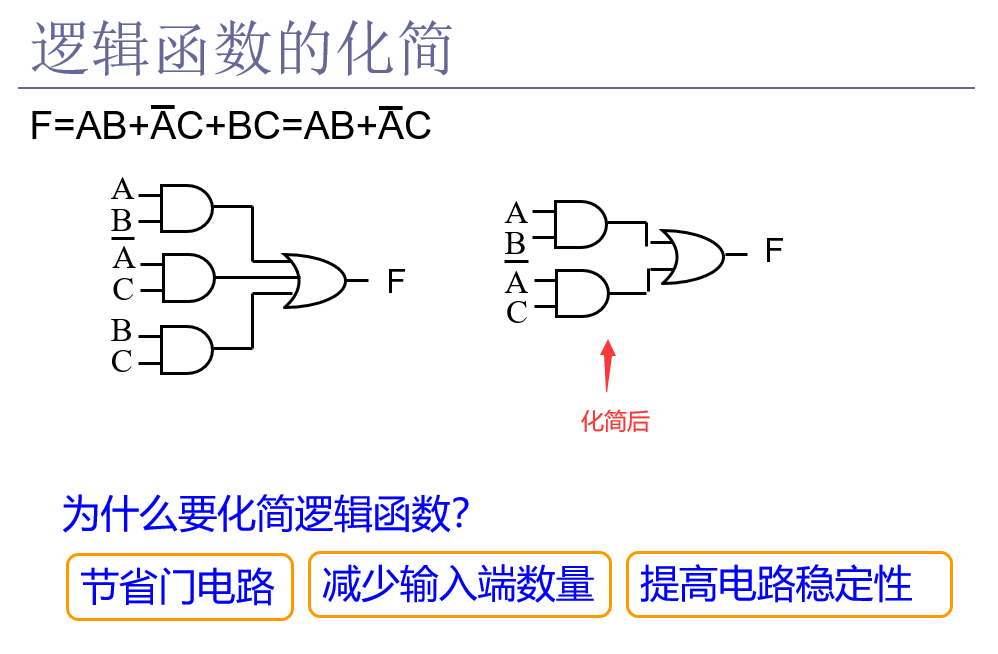
由此可以看到,函数化简是为了简化电路,以便用最少的门实现它们,从而降低系统的成本,提高电路的可靠性。
通常来说,我们化简的结果会有以下五种形式

为什么是这五种情况,这个跟我们实现的逻辑电路的元器件是有关系的。在所有的逻辑电路中,都是通过与、或、非三种逻辑电路来实现的,之前说过逻辑“与或”、“或与”、“与或非”组合逻辑电路是具有完备性的,也就是说能够通过它们不同数量的组合能够实现任何电路。
通过不同的“与或”电路组成的电路,最后化简的表达式就是“与或”表达式,其他同理。
二、将使用“与或”表达式的化简

-
表达式中乘积项的个数应该是最少的
表达了最后要用到的与门是最少的,因为每一个乘积项都需要一个与门来实现。同时也对应了或门输入端的个数变少,有2个与项或门就有2个输入端,有3个与项或门就有3个输入端。
所以第一个条件是为了我们的与门和或门最少。
-
每一个乘积项中所含的变量个数最少
它是解决每一个与门的输入端最少。
逻辑函授的化简有三种方法
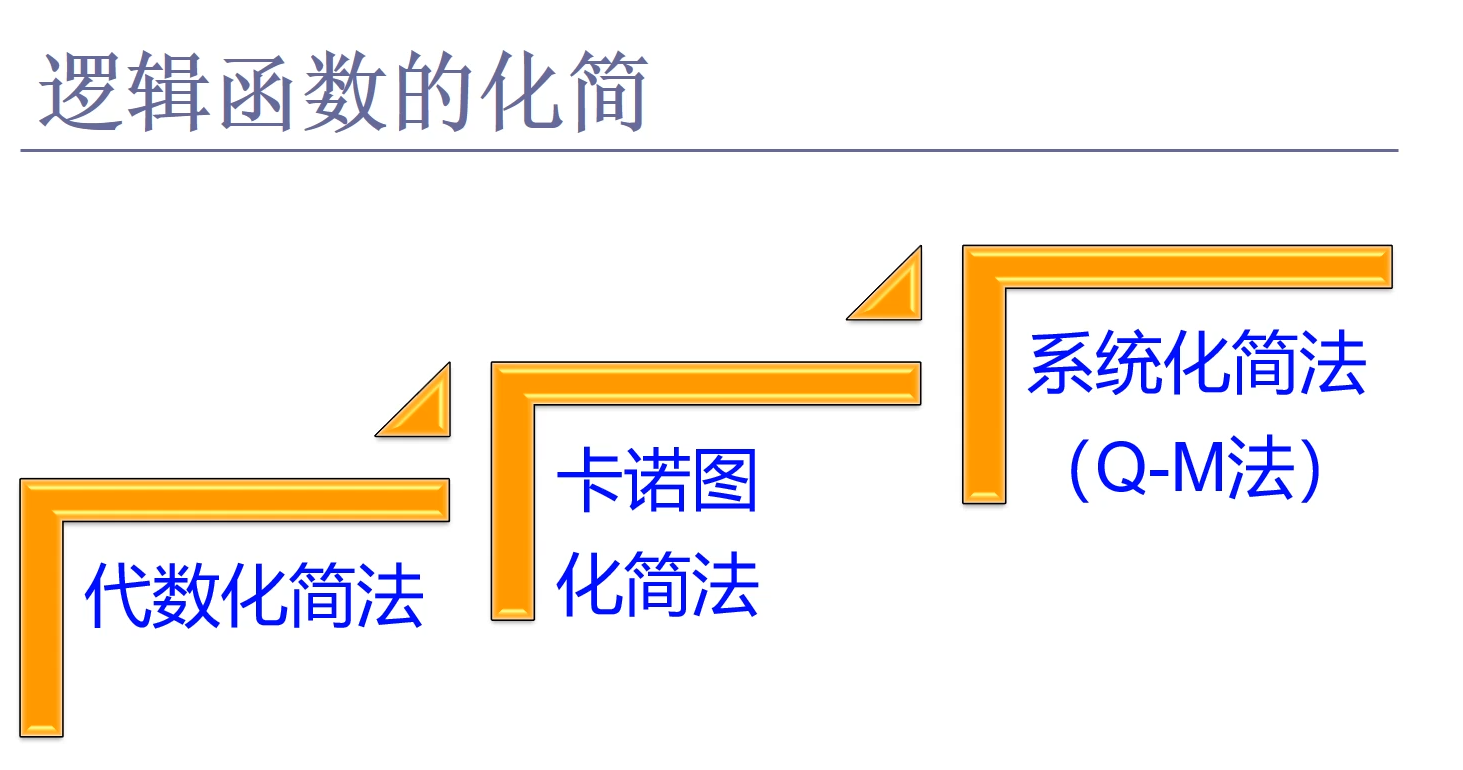
三、逻辑函数的代数化简法
3.1 并项法
并项法就是将两个逻辑相邻(互补)的项合并成一个项,这里就用到了“合并律”

将公因子A提取出来合并成一项,b和b非相或的结果就等于1,所以最后的结果就是A。
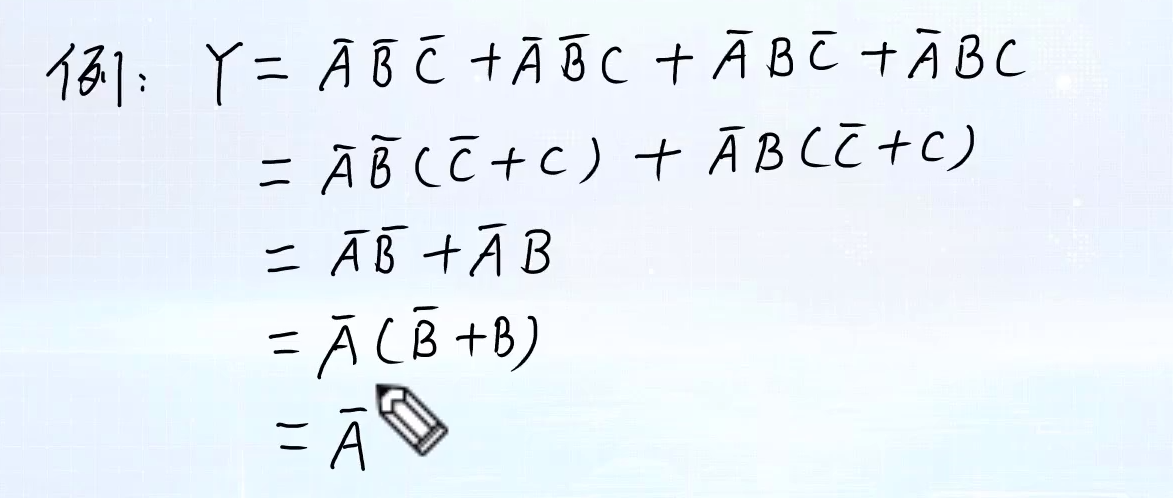


3.2 吸收法
吸收法是利用公式“吸收律”来消去多余的项
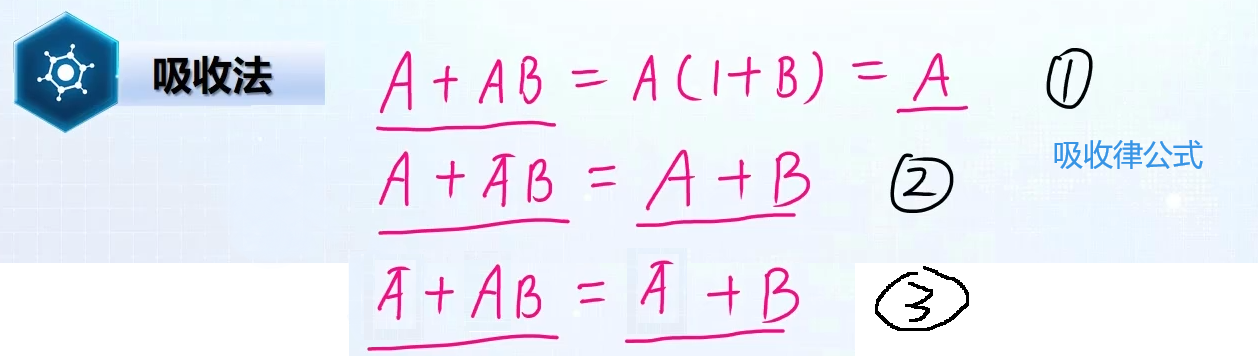
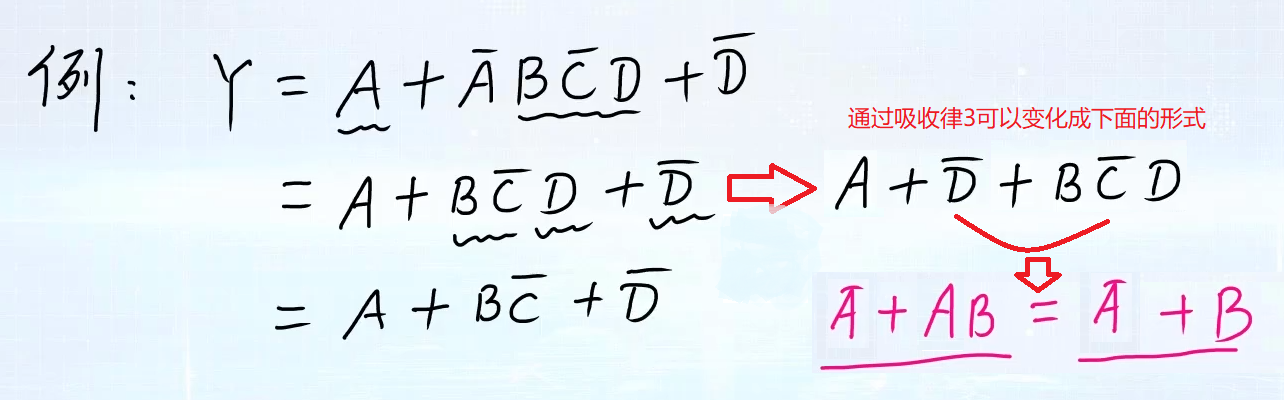

3.3 消项法
消项法又称为吸收律消项法


3.4 消因子法(消元法)

3.4 配项法

左边的例子用到了方法1,右边的例子用到了方法2。
3.5 逻辑函数的代数法化简的优缺点
优点:对变量的个数没有限制。在对定律掌控熟练的情况下,能把无穷多变量的函数化成最简。
缺点:需要掌握多个定律,在使用时需要能够灵活应用,才能把函数化到最简,使用门槛较高。在有些函数下,并不能化到最简。
综上所述,代数法化简的缺点远远大于它的优点,因而引出了卡诺图化简法。
四、卡诺图化简
4.1 概念
-
卡诺图是由美国工程师卡诺(Karnaugh)首先提出的一种用来描述逻辑函数的特殊方格图。
-
在学习卡诺图之前有个概念需要清楚:
-
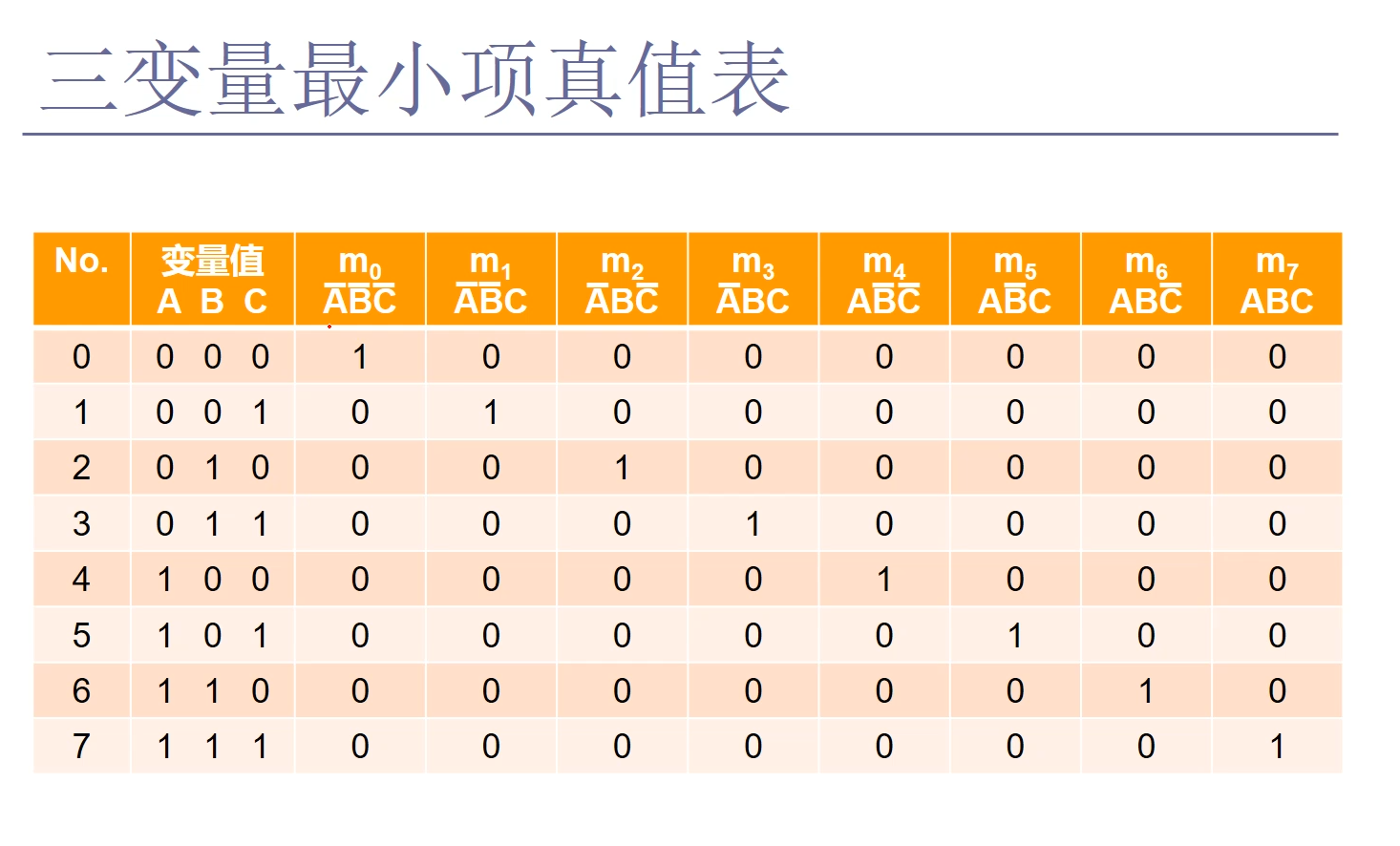
最小项的定义:一个函数的某个乘积项包含了函数的全部变量,其中每个变量都以原变量或反变量的形式出现,且仅出现一次,则这个乘积项称为该函数的一个标准积项,通常称为最小项。
简单来说最小项就是变量只有与非的表达式,3变量的与非表达式能够组合出8种不同的形式。它们的特点是8种不同的与非表达式,输入同样的变量取值,如:000,最后只有一种表达式会得1,其余得0,所以叫做最小项。
-
逻辑相邻最小项,如果两个最小项之间,只有一个变量不同,其余都相同,这个就叫做逻辑相邻最小项。
-
| 编号 | A | B | F |
|---|---|---|---|
| m0 | 0 | 0 | 0 |
| m1 | 0 | 1 | 1 |
| m2 | 1 | 0 | 1 |
| m3 | 1 | 1 | 0 |
这个真值表是AB变量的数值是按照顺序来变化的,可以看到编号为m1和m2之间变量并不相邻,都互相取反了。我们可以通过调整顺序,将这个真值表变成逻辑相邻(格雷码)。
| 编号 | A | B | F |
|---|---|---|---|
| m0 | 0 | 0 | 0 |
| m1 | 0 | 1 | 1 |
| m3 | 1 | 1 | 0 |
| m2 | 1 | 0 | 1 |
将m3和m2进行位置的互换以后,可以看到只有1位变量的值,发生了变化,这样就叫做逻辑相邻(格雷码)。

逻辑相邻(格雷码)给我们找到了一个化简的途径,在卡诺图中正是利用了这个原理进行化简的。
4.2 卡诺图的构成
卡诺图主要的做法就是画一个二维的方格图,在这个图里面,我们把逻辑相邻的最小项都摆放成位置相邻。
-
在这个方格图中,每一个方格代表逻辑函数的一个最小项,而且几何相邻(在几何位置上,上下或左右相邻)的小方格具有逻辑相邻性(格雷码),即两相邻小方格所代表的最小项只有一个变量取值不同。
-
对于有n个变量的逻辑函数,其最小项有2^n个。因此该逻辑函数的卡诺图由 2^n 个小方格构成,每个小方格都满足逻辑相邻项的要求。
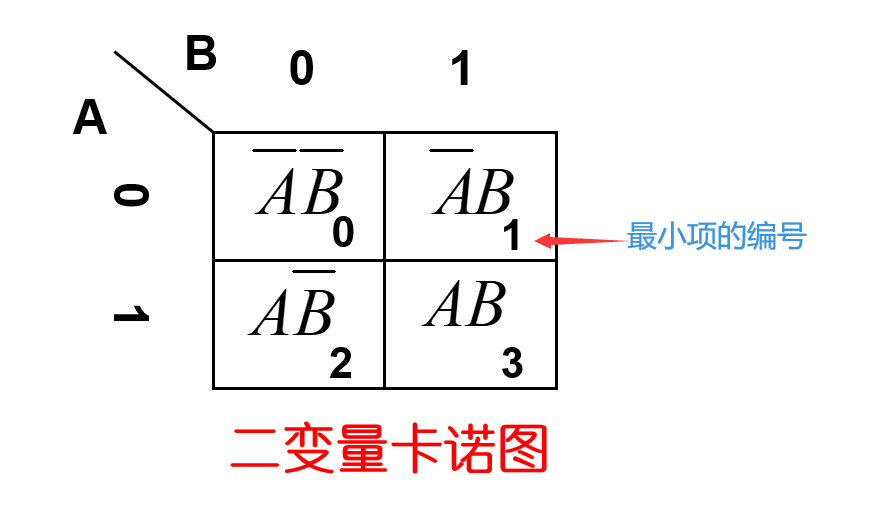
这是一个二变量的卡诺图,变量A写在左侧,0和1表示那一列A不同的取值。变量B写在上方,0和1表示那一行B不同的取值。格子里面是存放的是左侧与上侧的变量结合出来的最小项表达式。结合成最小项时,左侧的变量A在高位,上侧的变量B在低位。
相邻方格位置之间的最小项只有一个变量发生了变化,这个就叫做位置相邻。
在卡诺图中多变量那一行,需要按照逻辑相邻(格雷码)的概念进行排序。
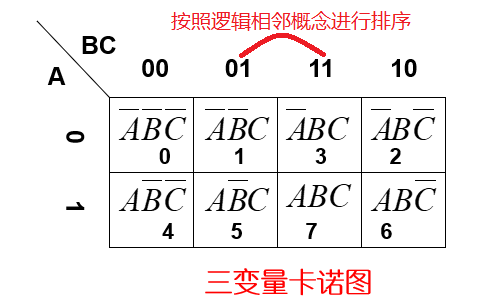
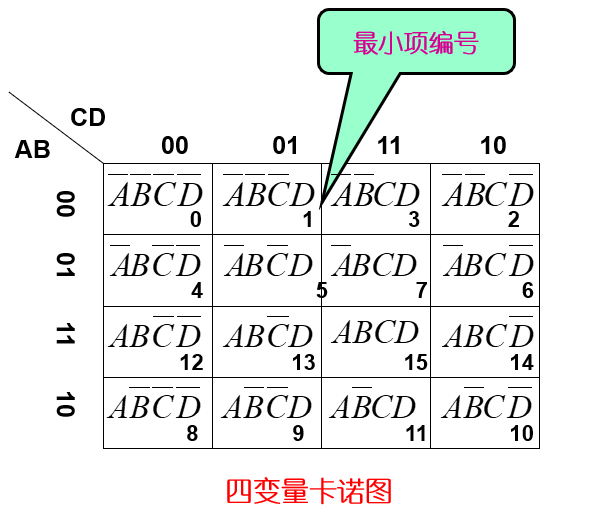
N变量的表达式有N种不同的最小项,这个原理在卡诺图中也是一样的。在N变量的卡诺图中,任意位置的最小项都能找到N个对应位置相邻的最小项。
最小项编号具有格雷码的循环特性,所以在卡诺图中边缘的最小项能够跟它最上面和最左、右边的最小项位置相邻。
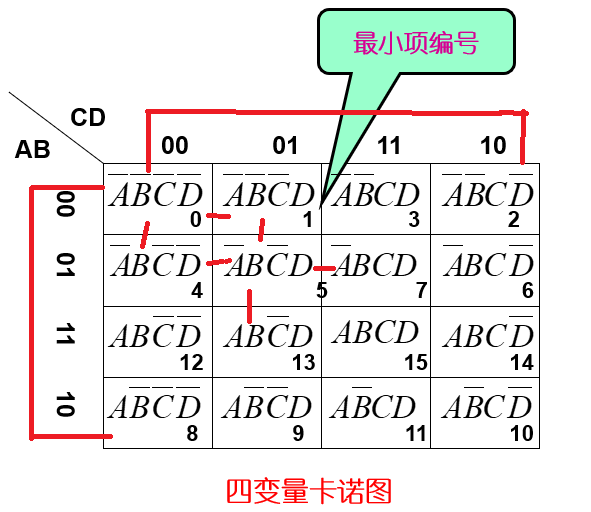
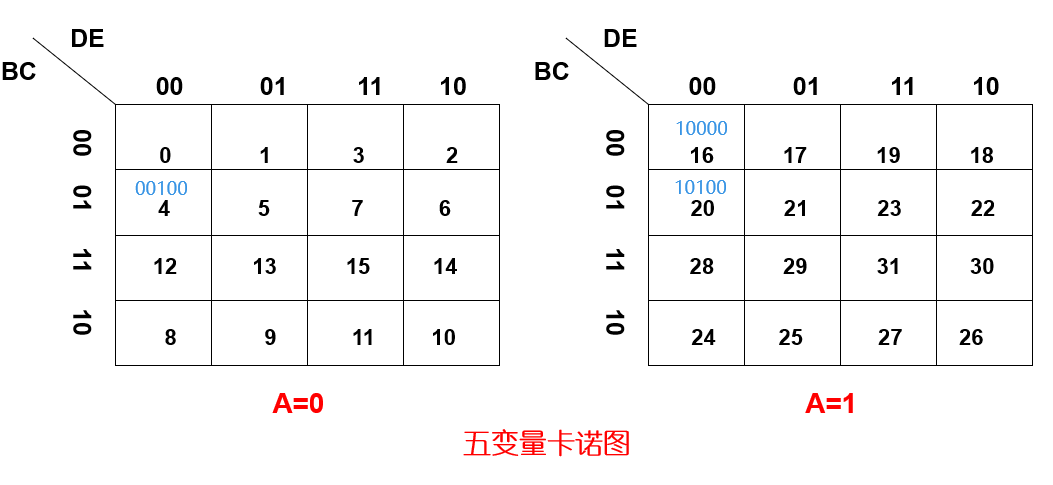
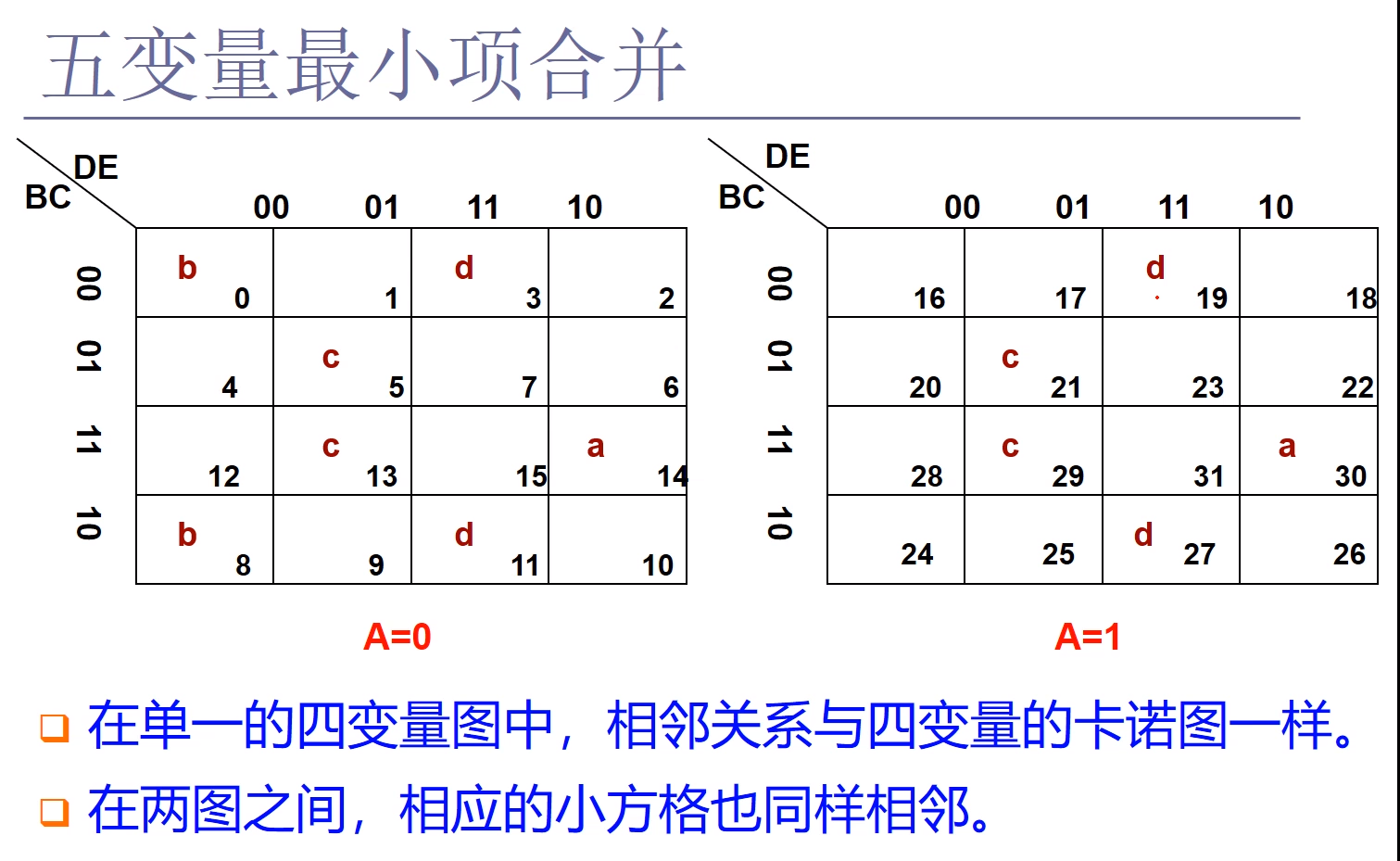
对于5变量的卡诺图,我们也应该提供给每一个最小项都有5个位置相邻的最小项。但是在二维表中,只有上下左右,因此没有办法在一个表中提供5个位置相邻的最小项。那么一张不行,我们就把它定义成2张卡诺图。
假设,5个变量分别为:ABCDE,我们把A变量单独拿出来,将A=0的情况,用一张表来表示;将A=1的情况,再用一张表表示。每个表都是4变量的卡诺图,结合成最小项时,A变量在最高位,接下来是左侧的变量BC,上侧的变量DE在低位。

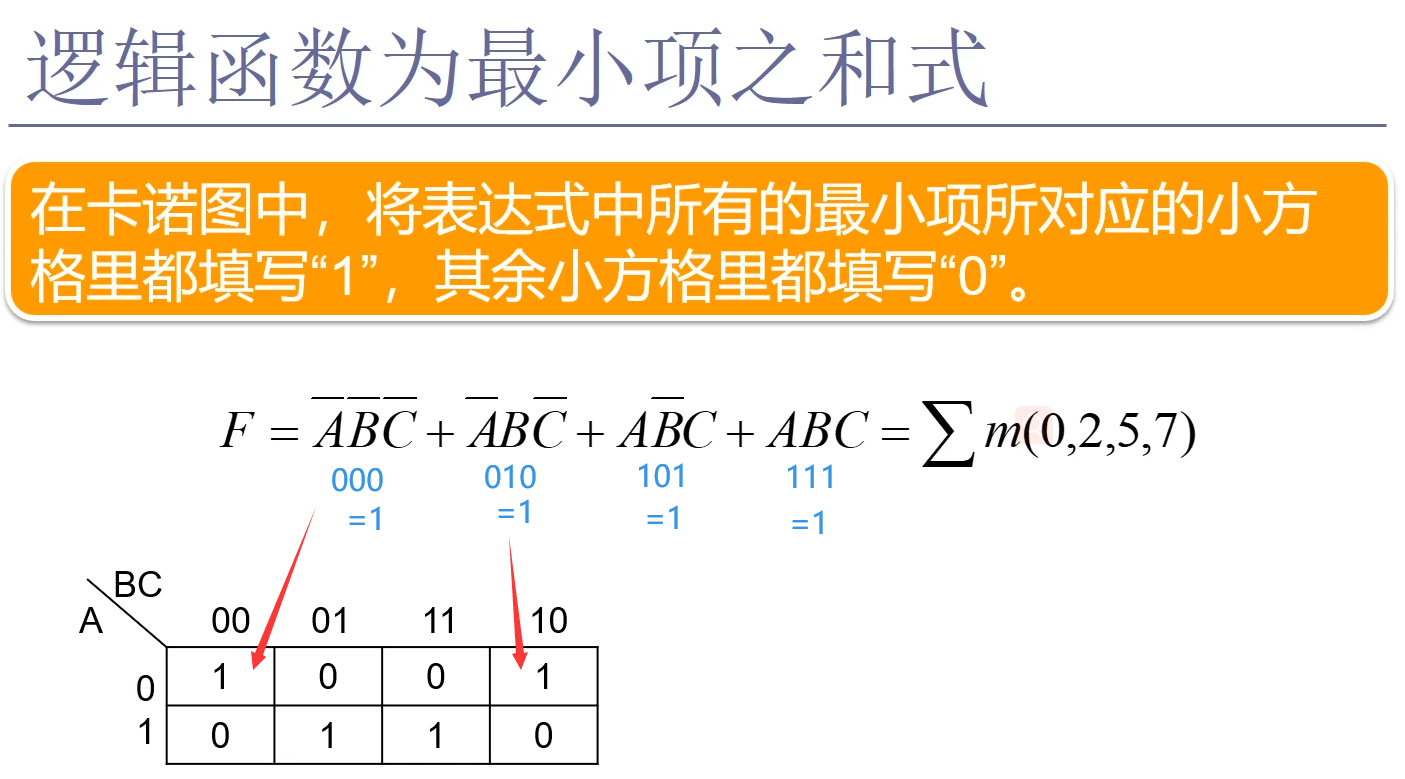
4.3逻辑函数的卡诺图表示

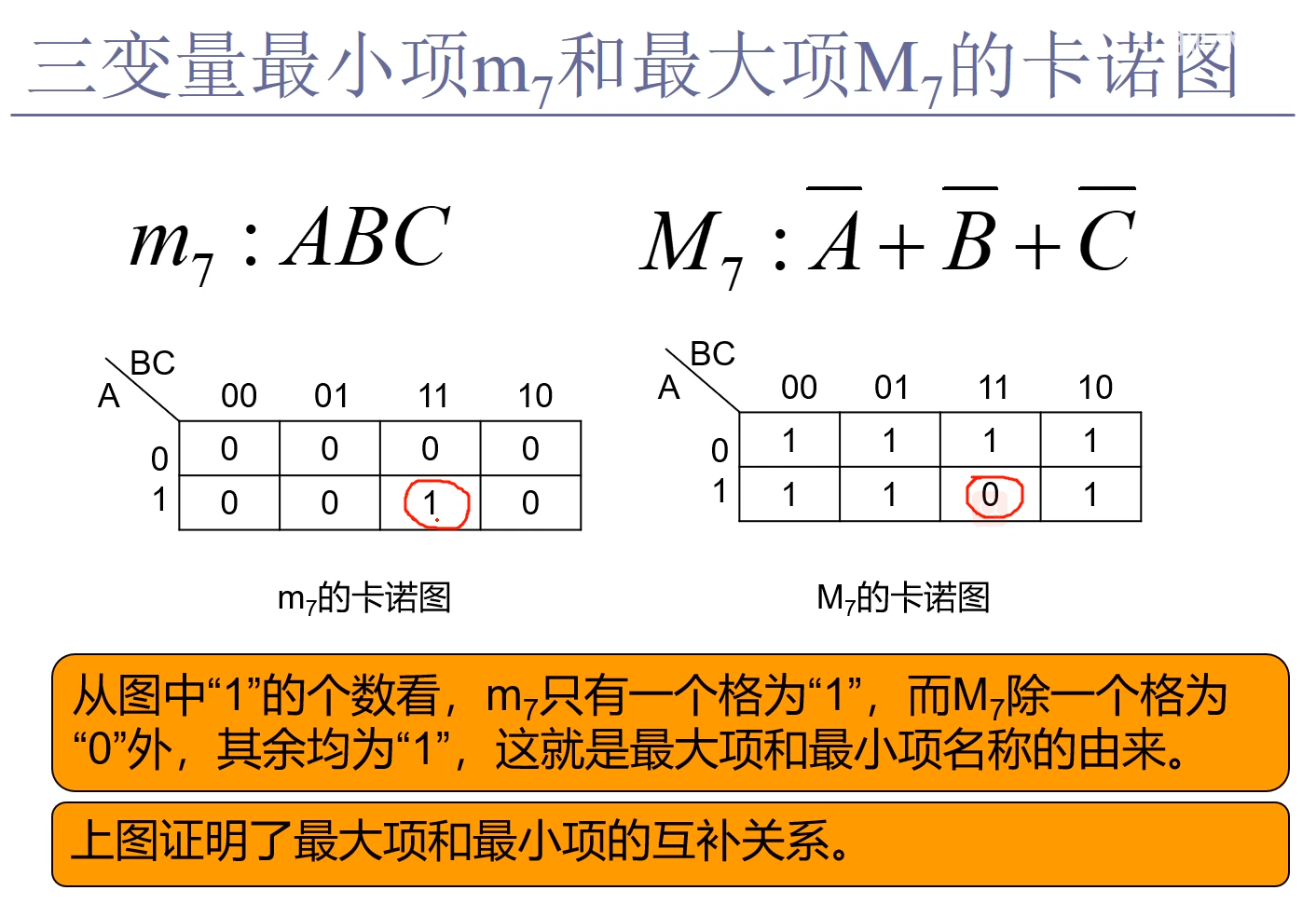
最小项之和式
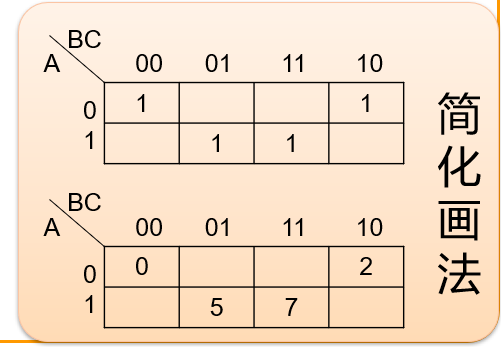
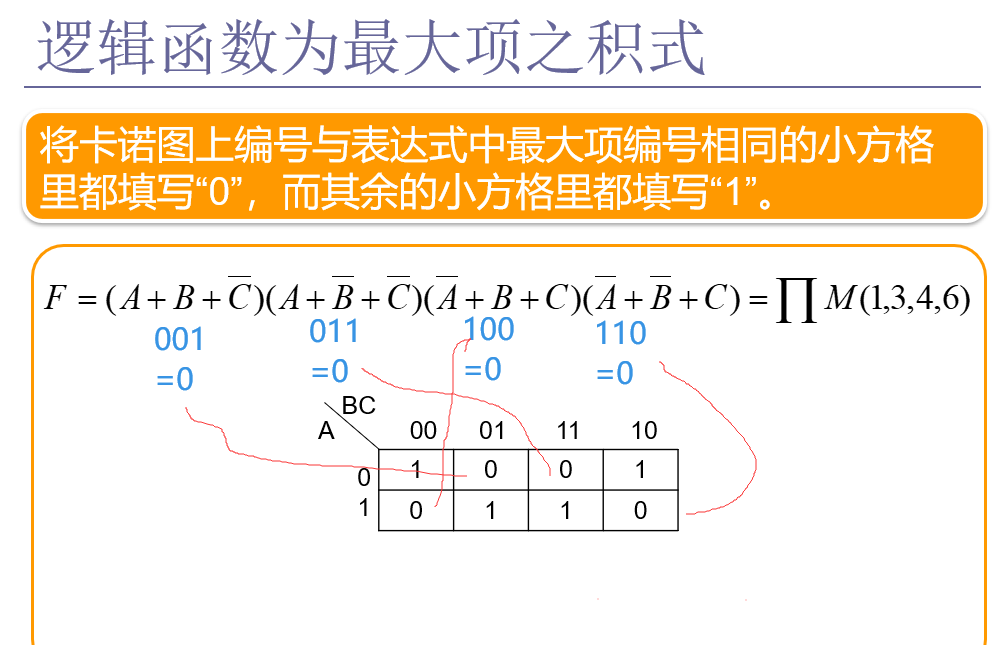
最大项之积式
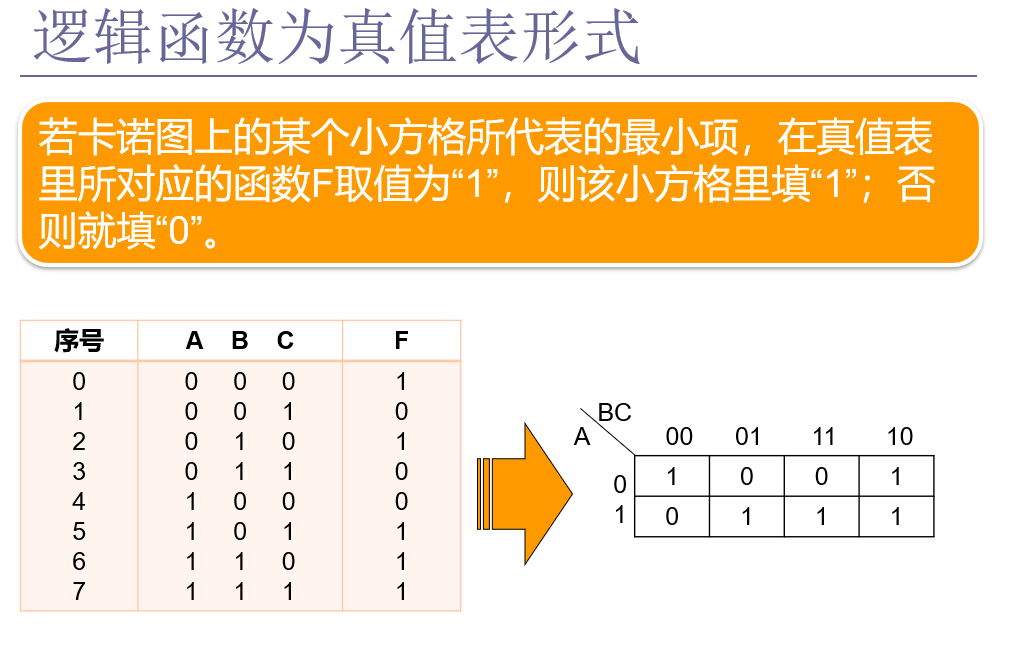
4.4 真值表转换成卡诺图
4.5 一般“与或”式的逻辑函数转换成卡诺图
1、将式子的不同变量提取出来,变成N变量的卡诺图。
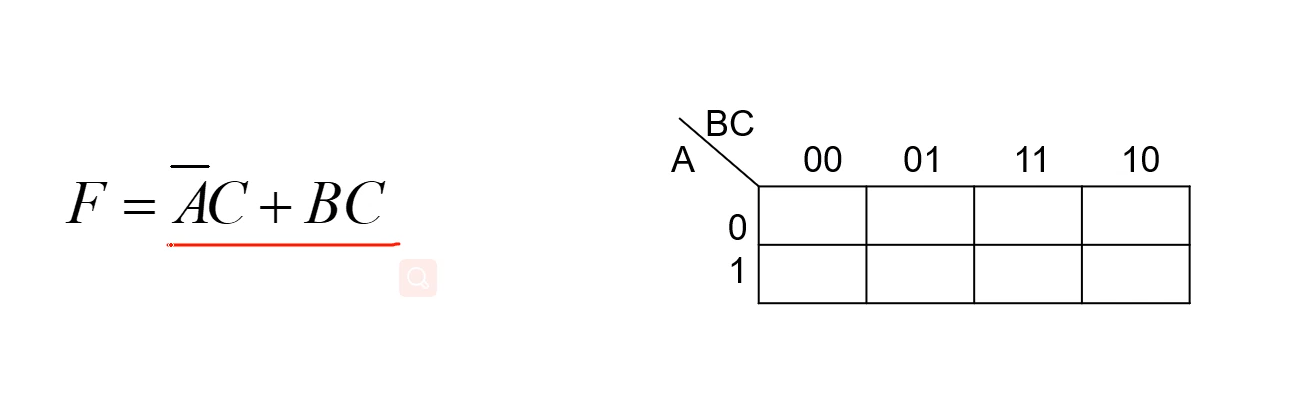
2、观察结果F 在何种状态下结果会变为1,上面式子通过观察可知,只要有一个与项的结果等于1,其结果F就会等于1.
3、将会使结果F等于1的变量值和卡诺图对应上,其格子填上1。
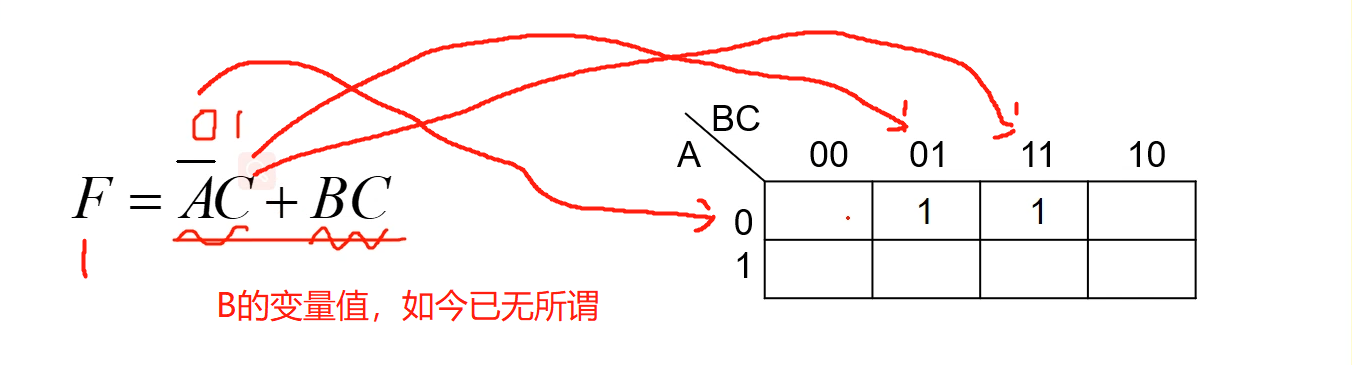
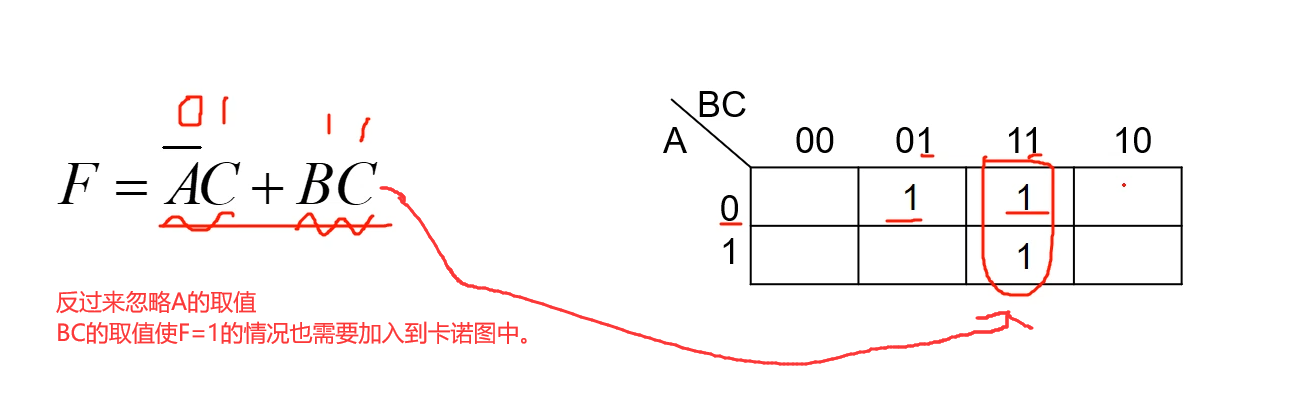
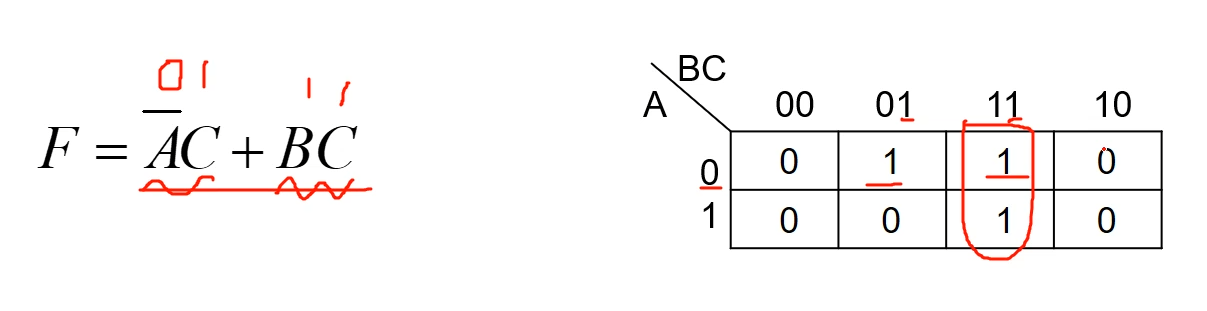
4、所有F=1的情况,列出来以后,其他就=0了。
4.6 一般“或与”式的逻辑函数转换成卡诺图
1、将式子的不同变量提取出来,变成N变量的卡诺图。
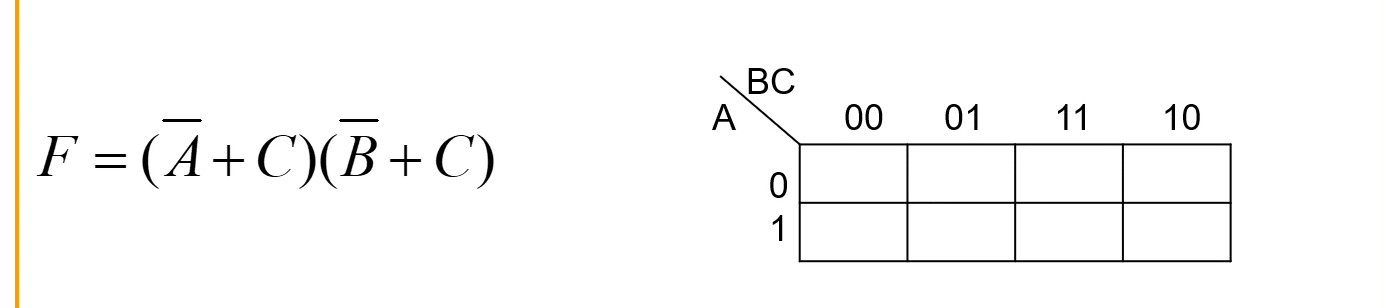
2、观察结果F 在何种状态下结果会变为0,上面式子通过观察可知,只要有一个或项的结果等于0,其结果F就会等于0.
3、将会使结果F等于0的变量值和卡诺图对应上,其格子填上0。
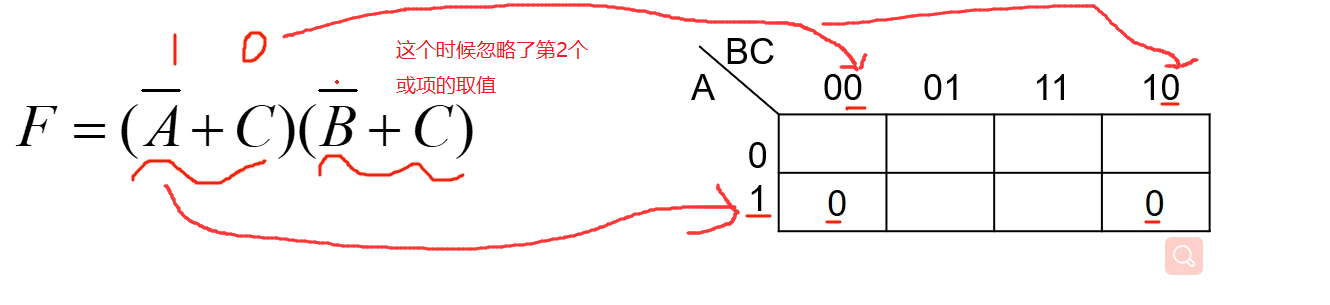
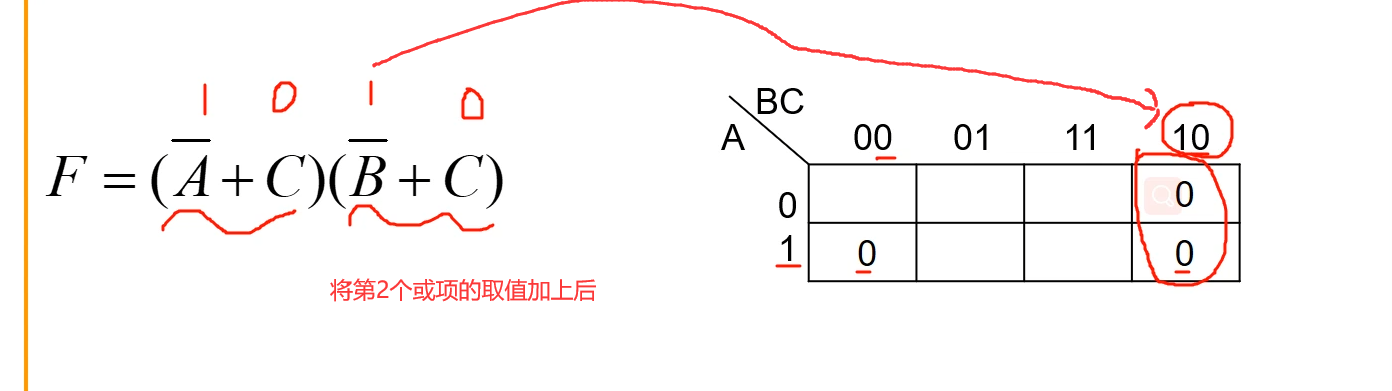
4、所有F=0的情况,列出来以后,其他就=1了。
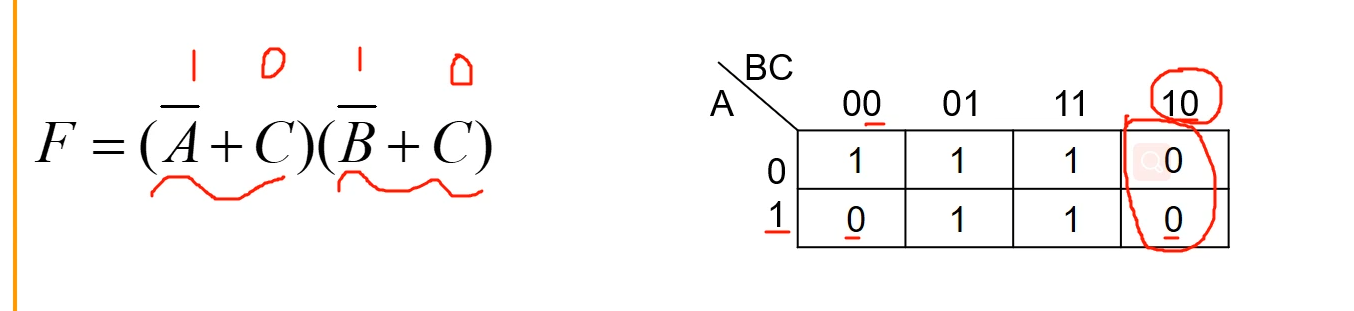
4.7 逻辑函数为其他形式转换成卡诺图


4.7 卡诺图的性质
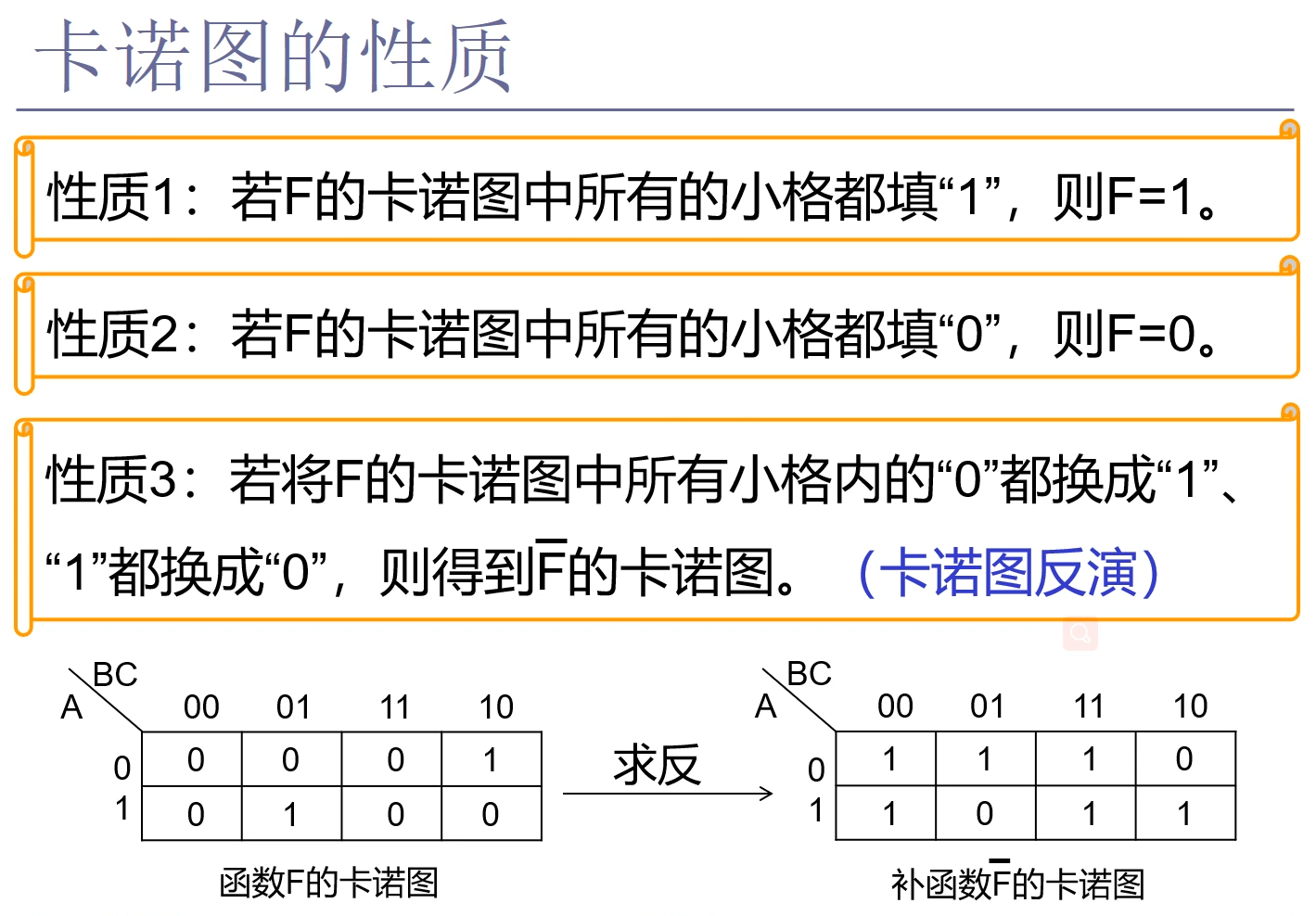
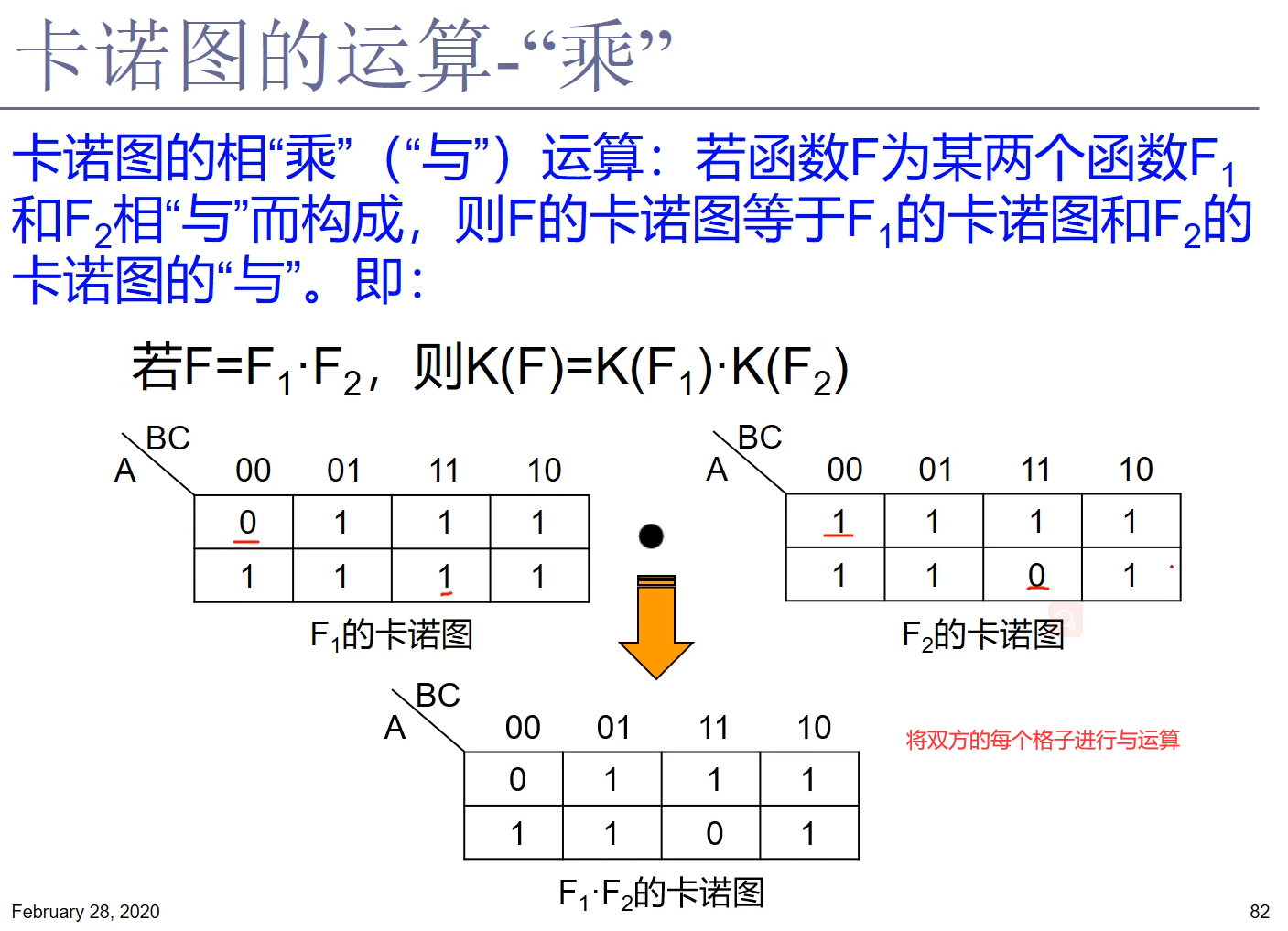
4.8 卡诺图的运算
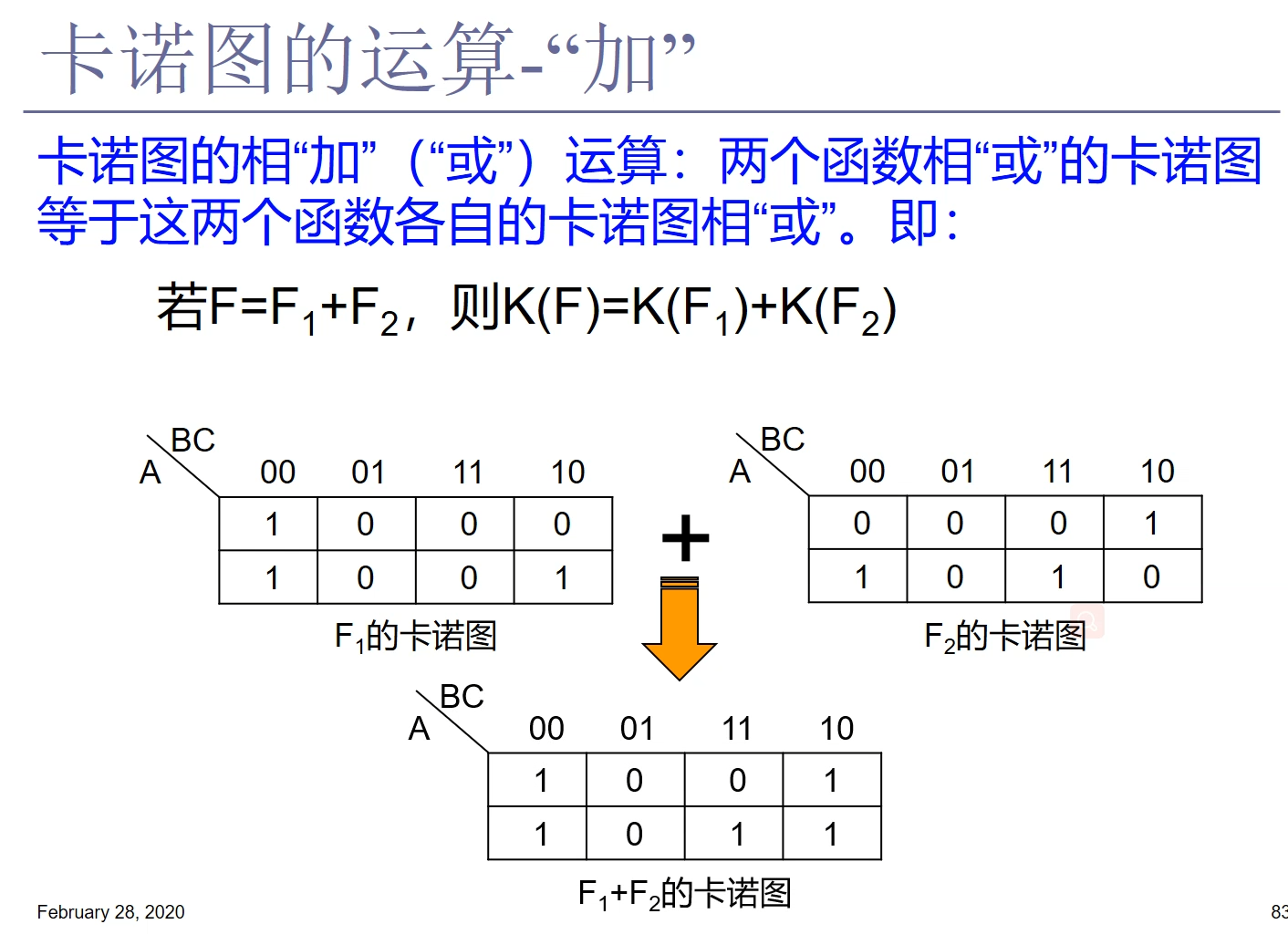
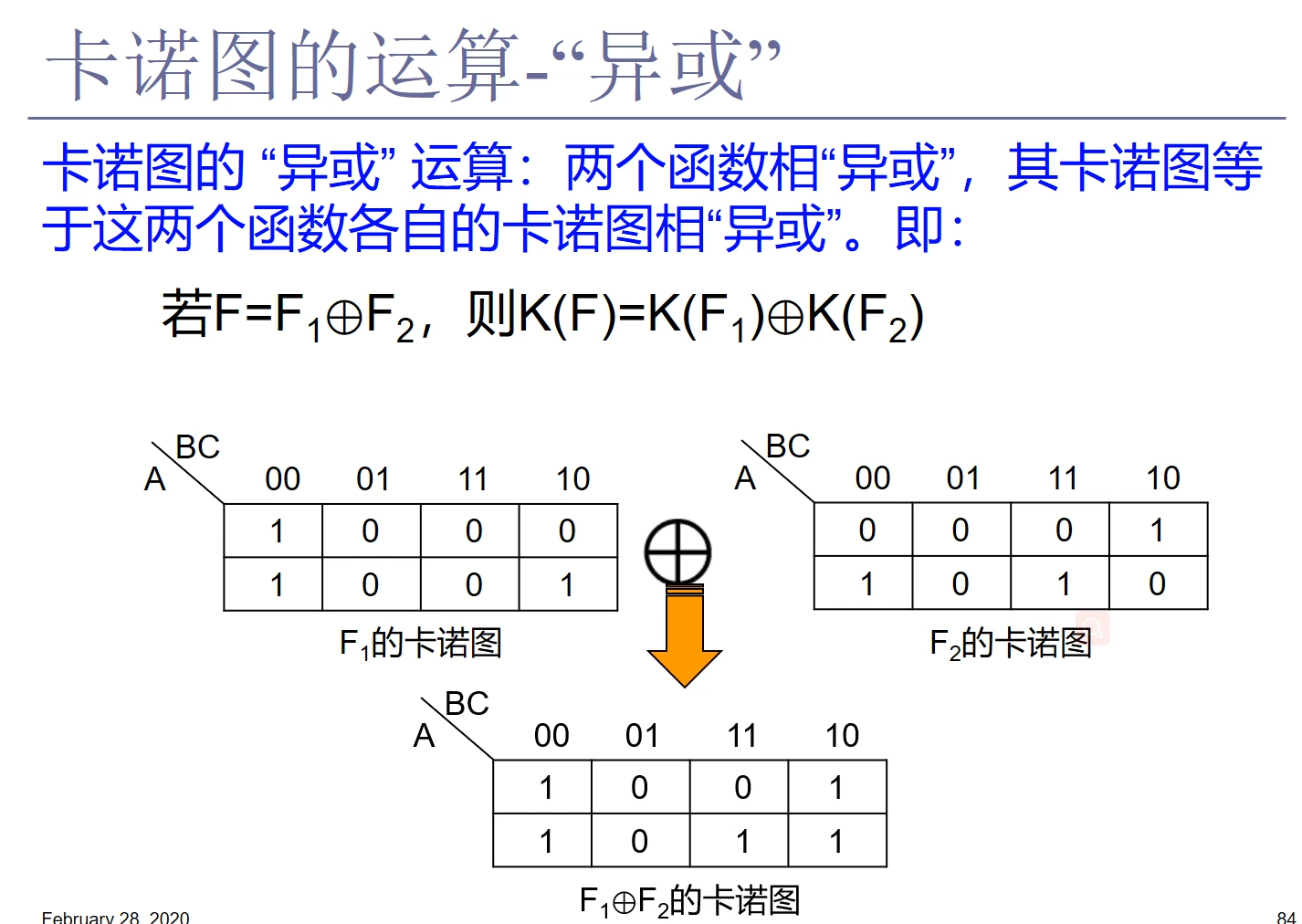

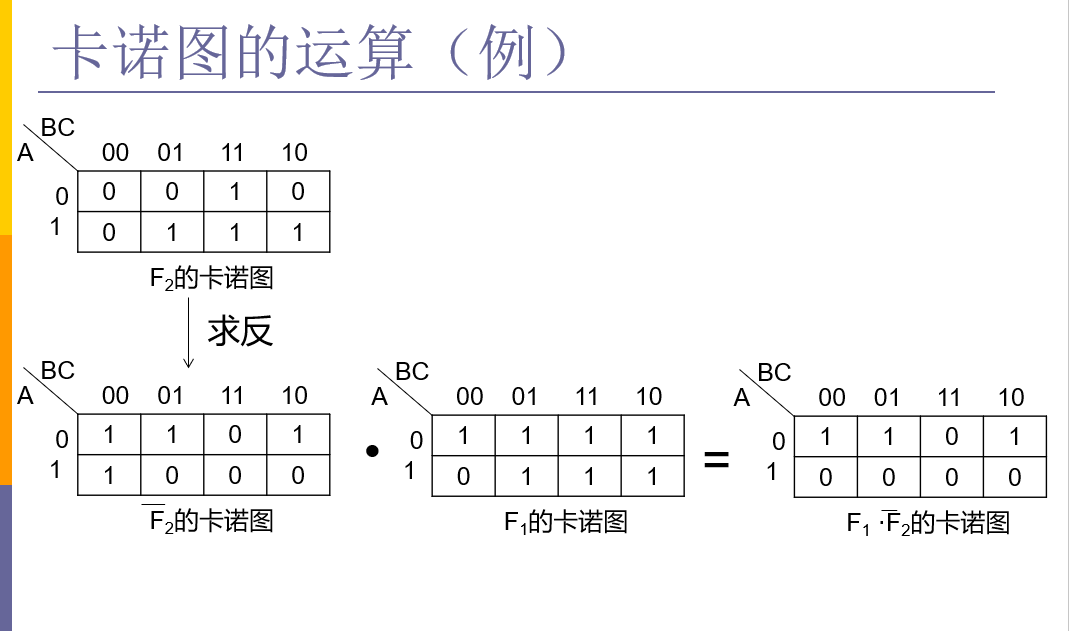
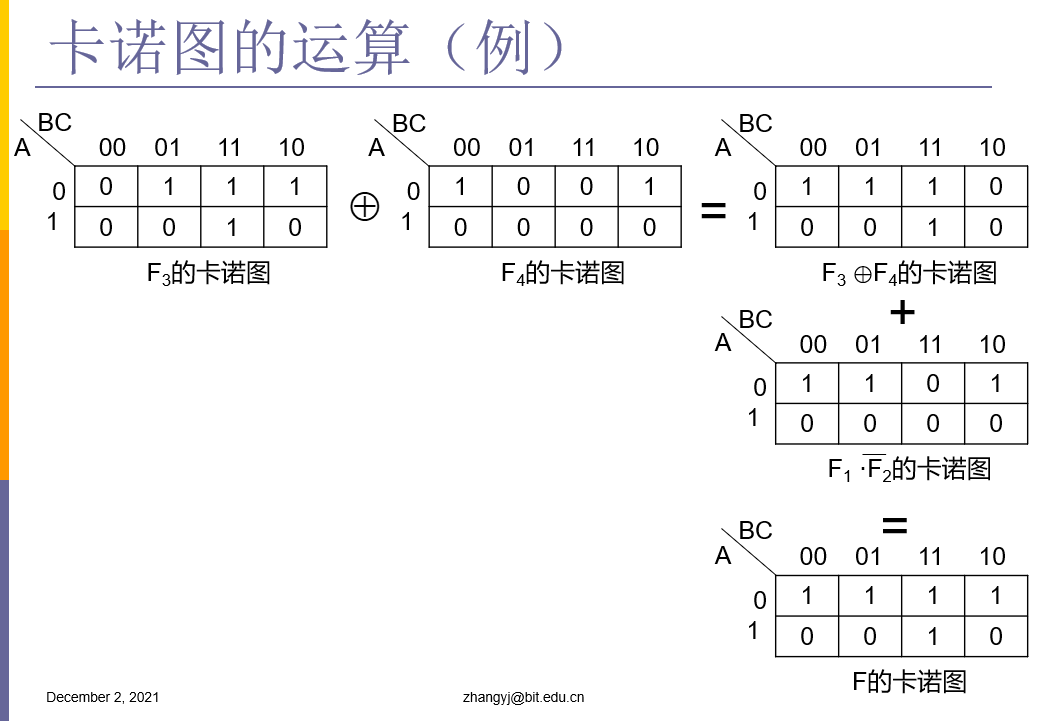
4.9 利用卡诺图化简逻辑函数
4.9.1 最小项合并规律

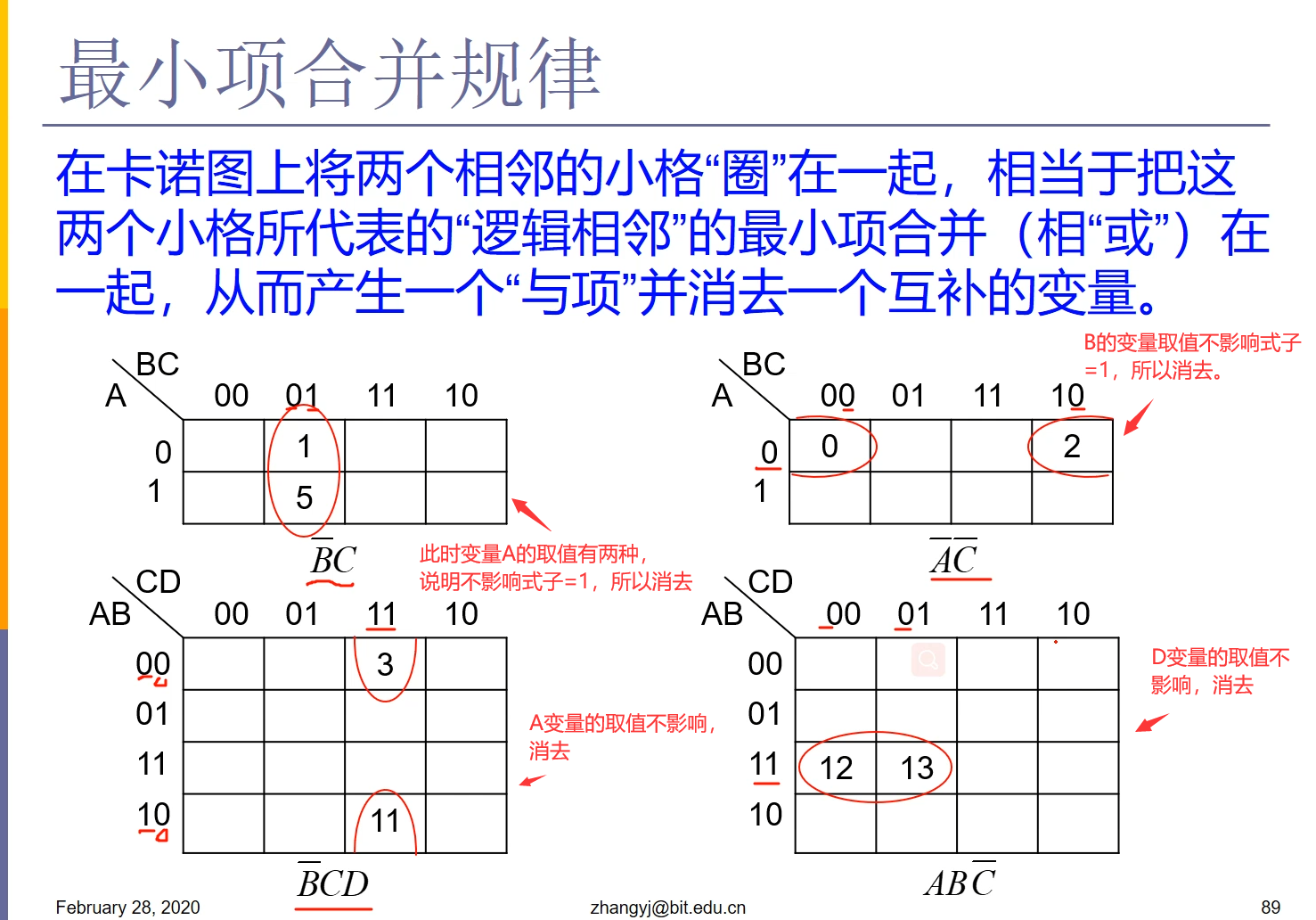
这个圈就叫做卡诺圈。
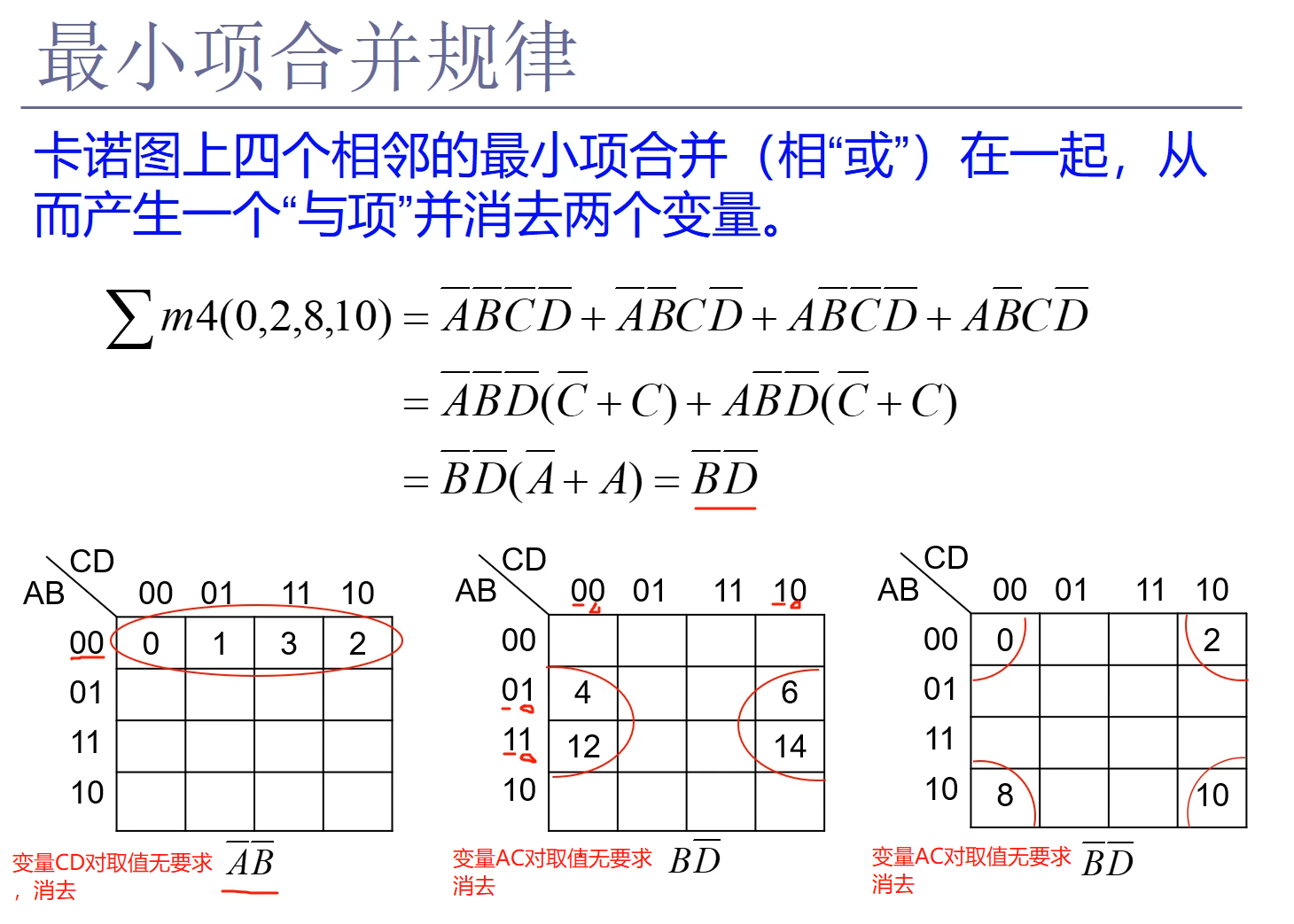
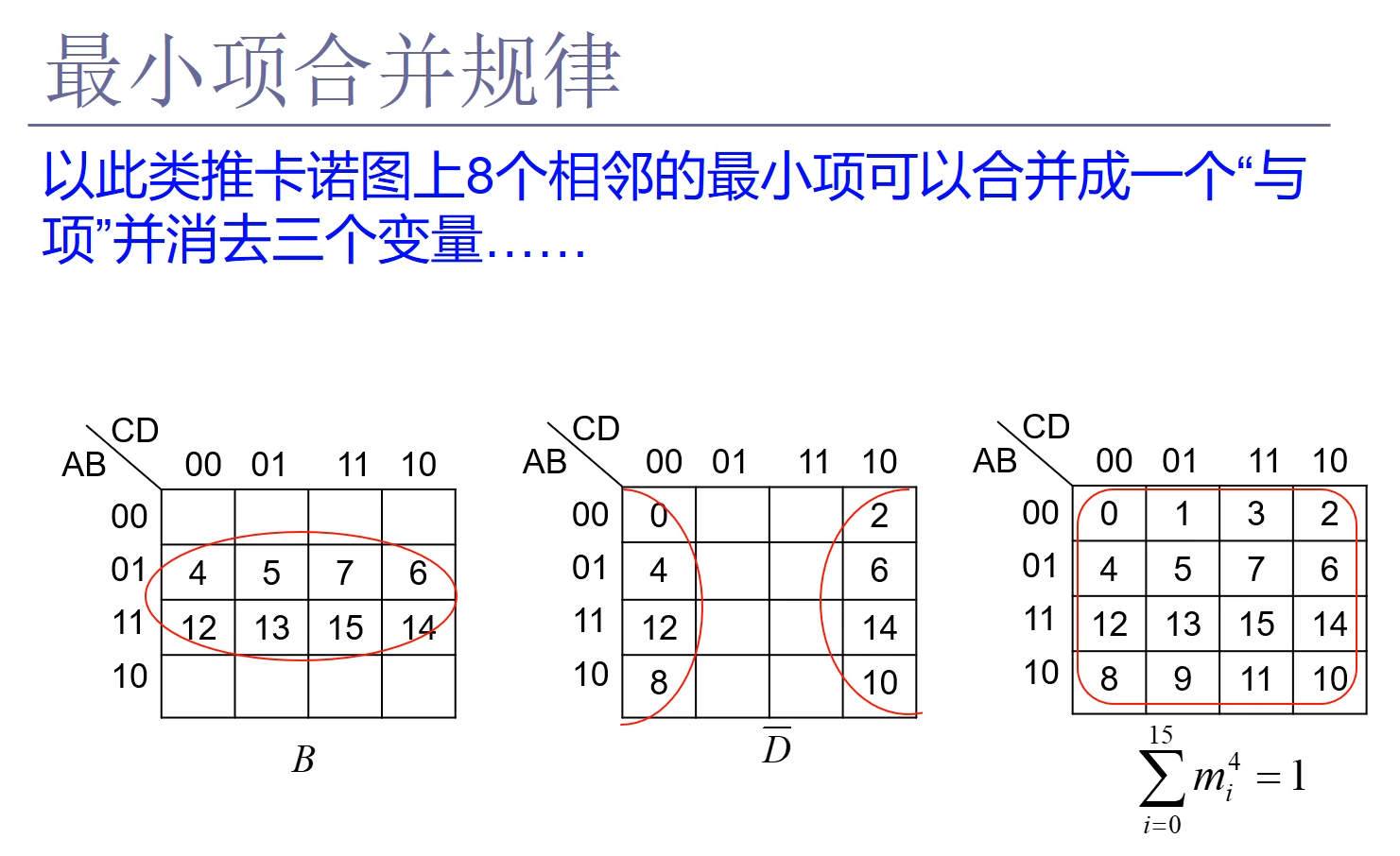
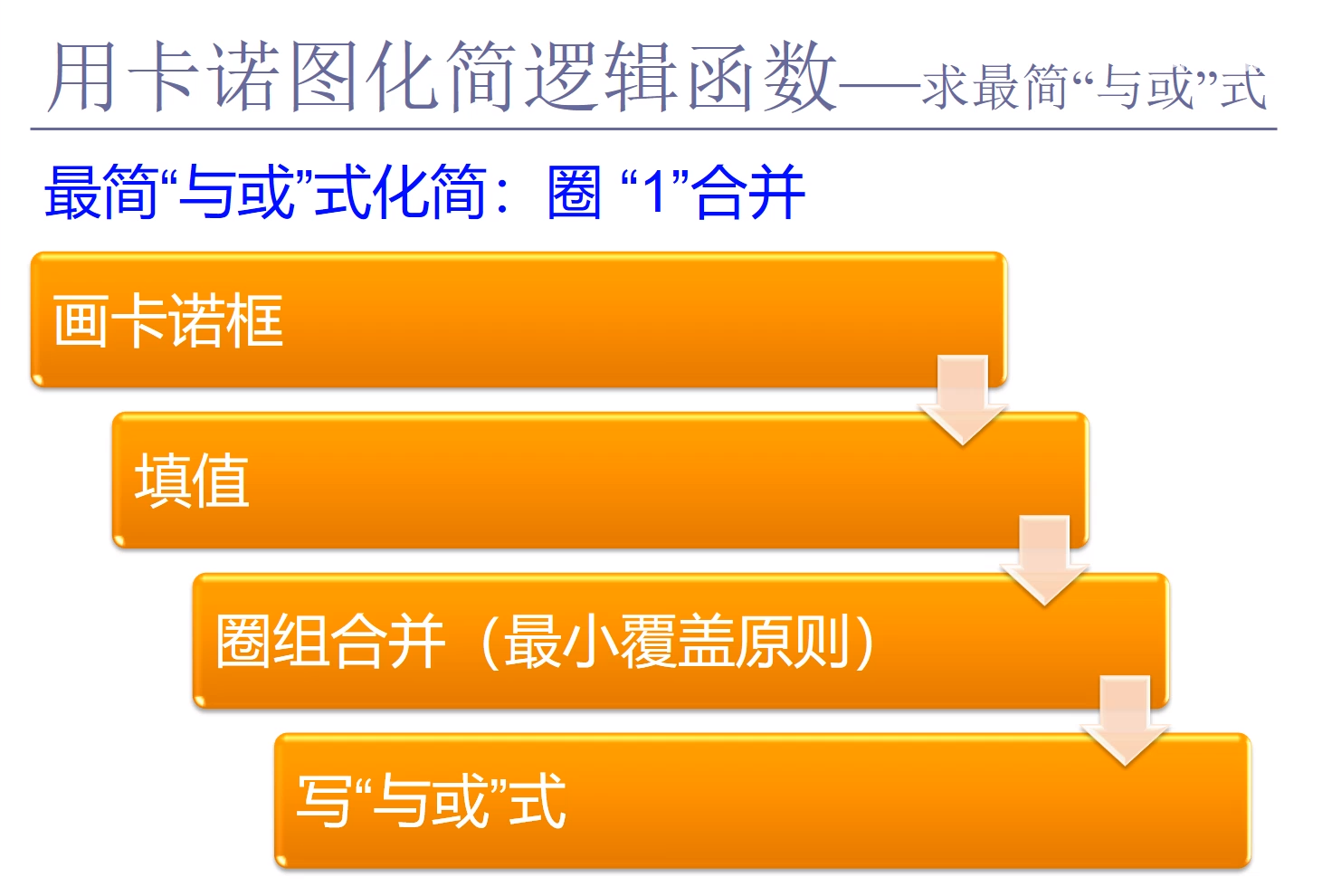
1、求最简“与或”式(最小项)


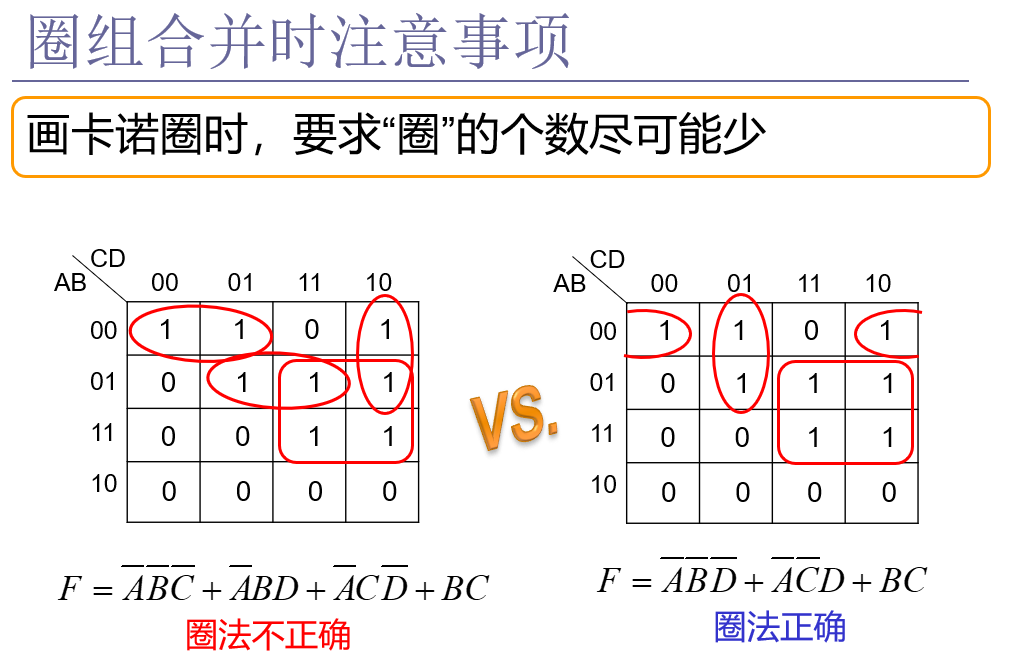
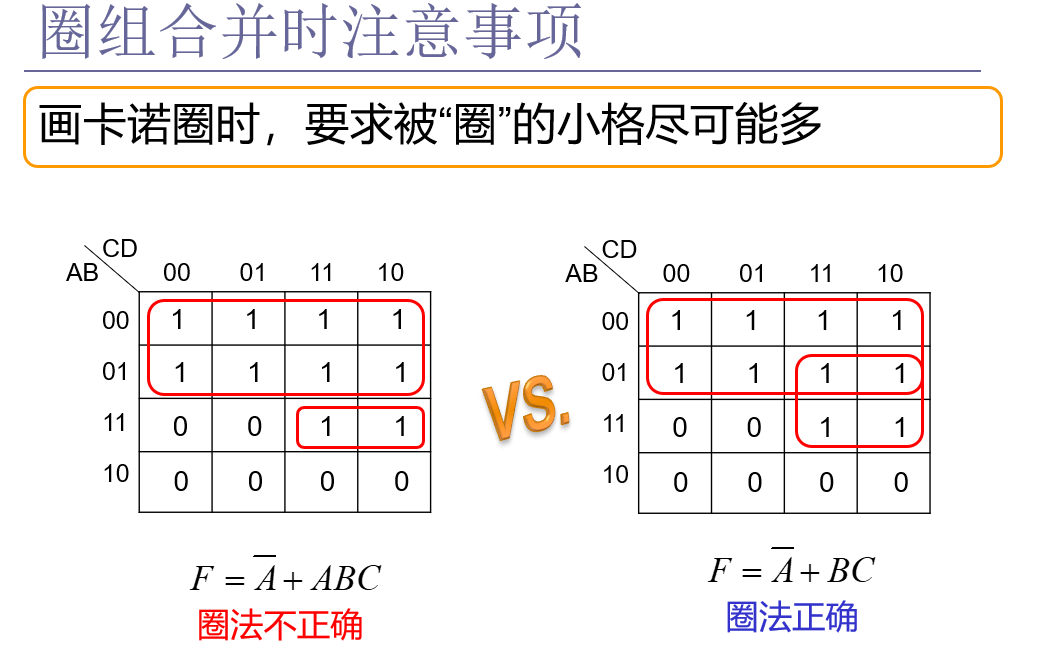
2、圈组合并时注意事项
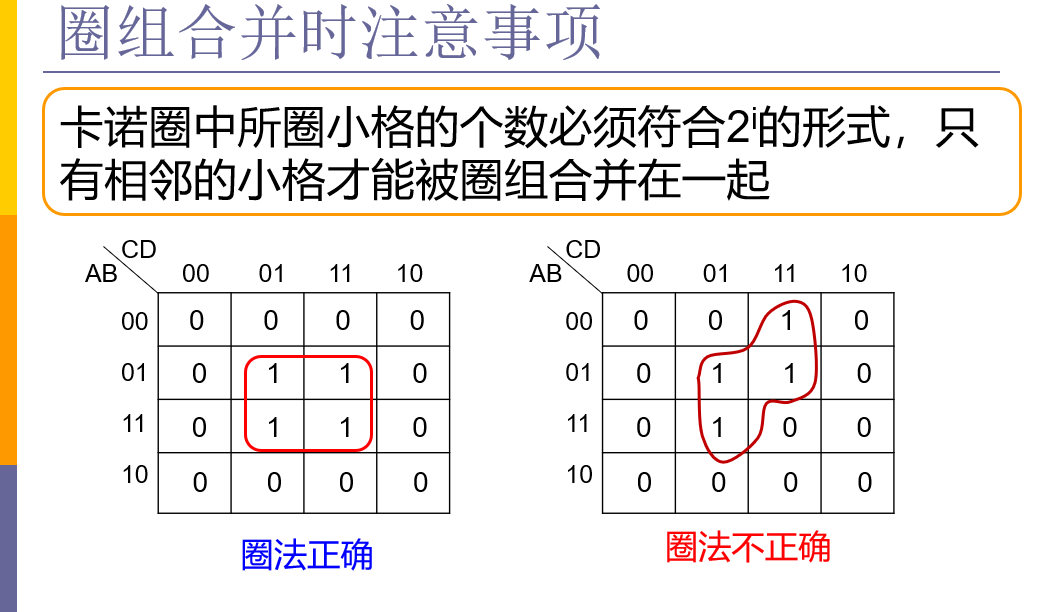
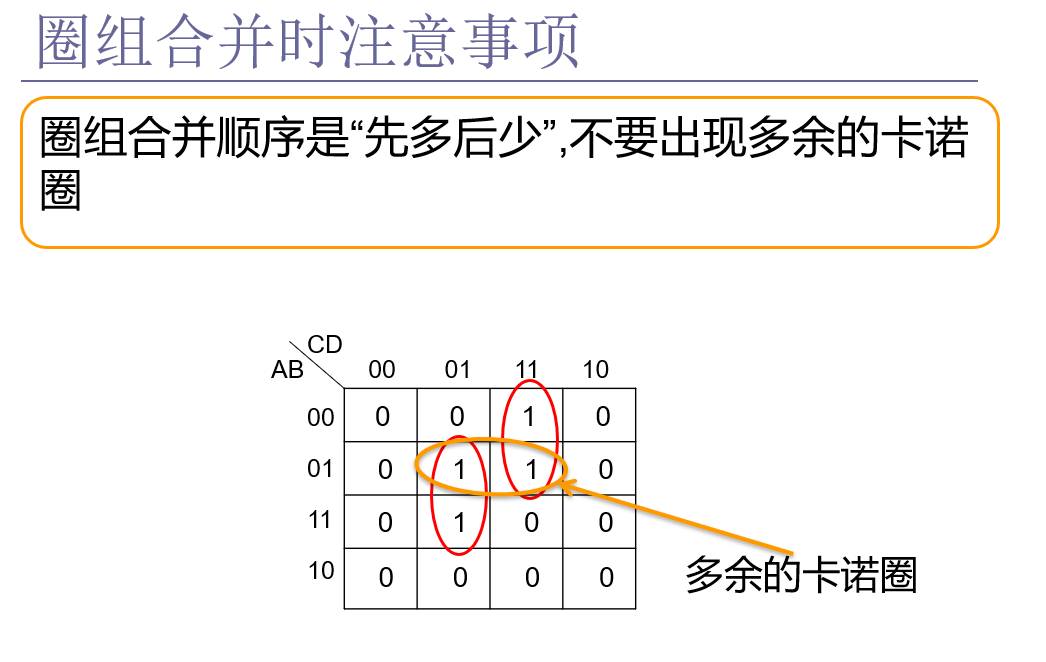
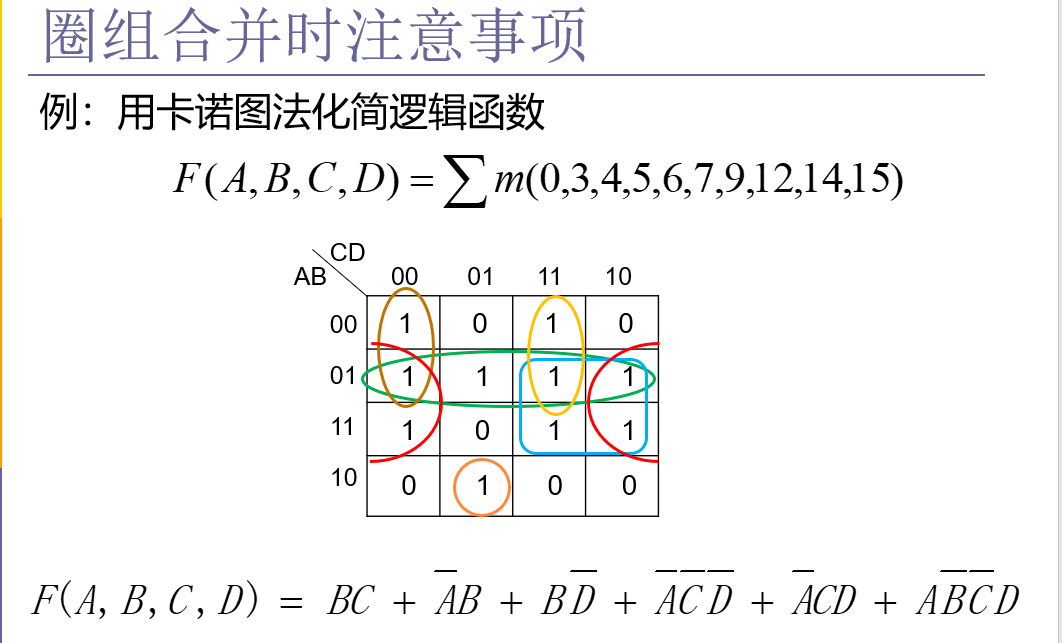
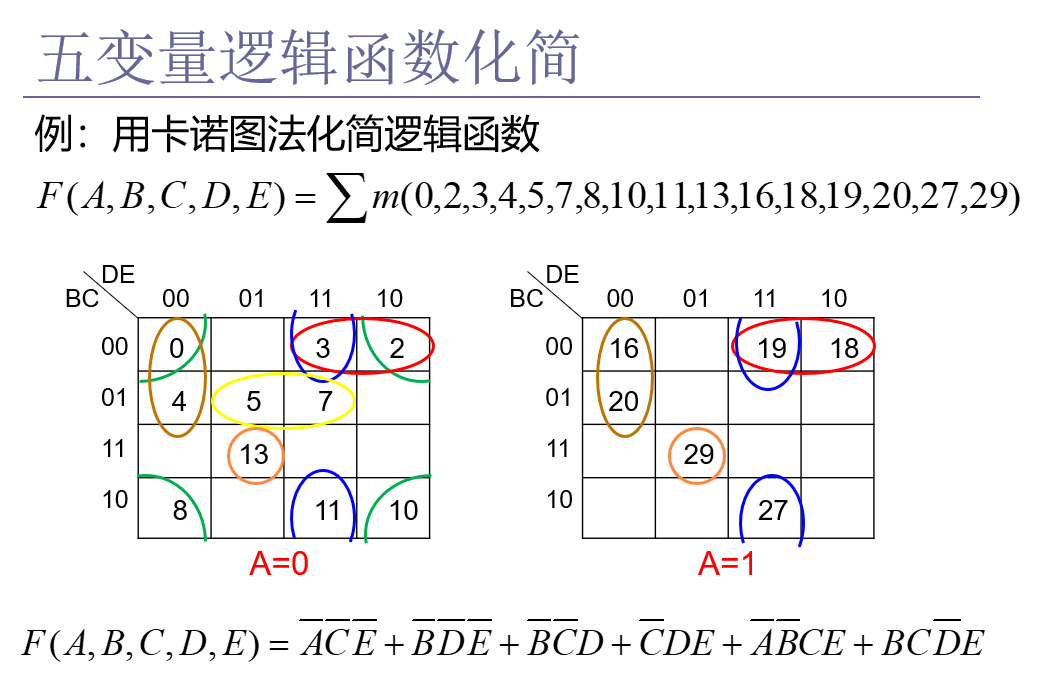
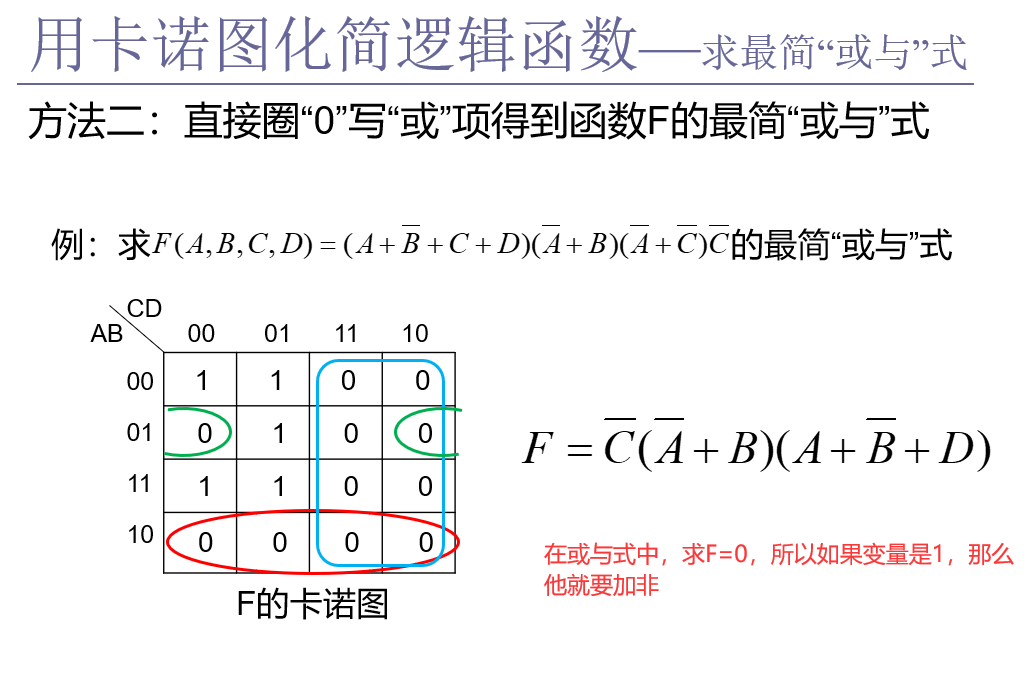
3、求最简“或与”式(最大项)

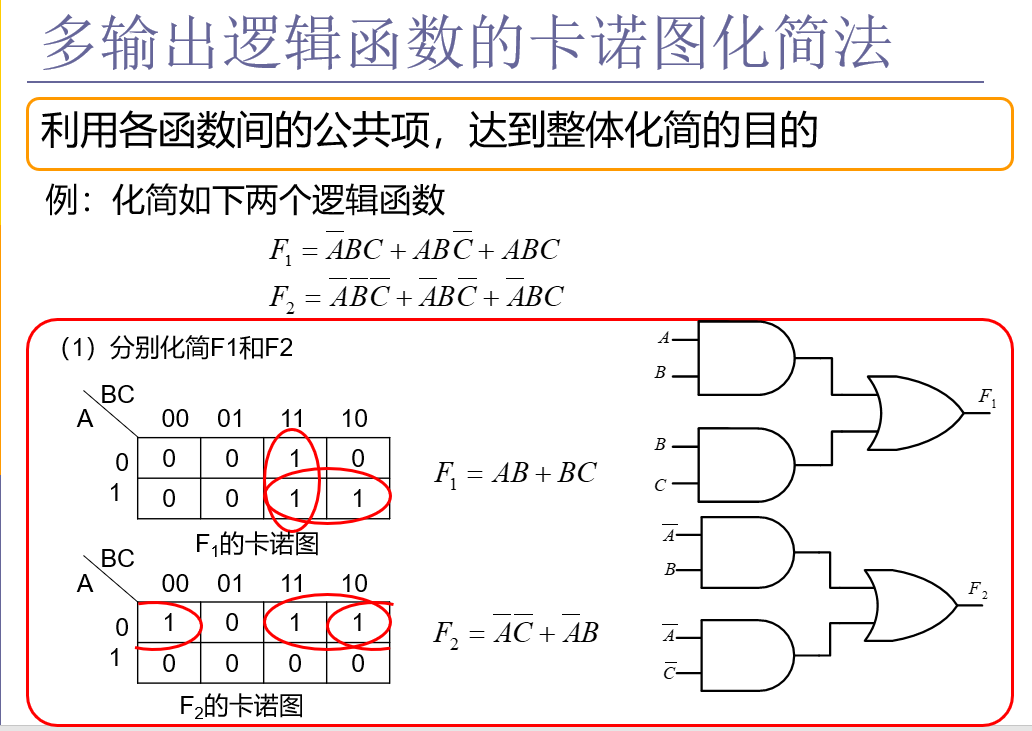
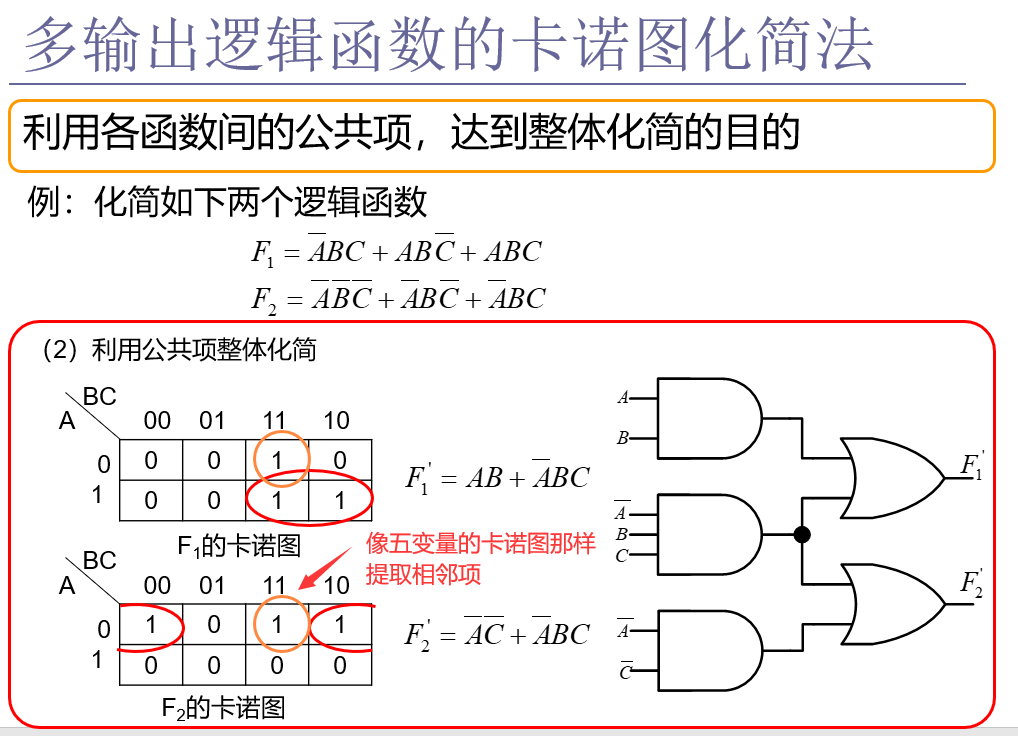
4.9.2 多输出逻辑函数的卡诺图化简法