5、逻辑代数的基本定律和规则
一、逻辑代数基本定律、公理
什么是公理,公理就是不需要证明就能成立的事实。逻辑代数公理主要说的是:逻辑常数“0”和“1”的基本运算规则。
在小学的时候,我们有学过一些关于加法和乘法的运算规律,那么同理这些运算规律在逻辑代数中也是能够成立的。
如:加法交换率

套用在逻辑代数中,就变成了这样:
1. 变量和常量的关系式
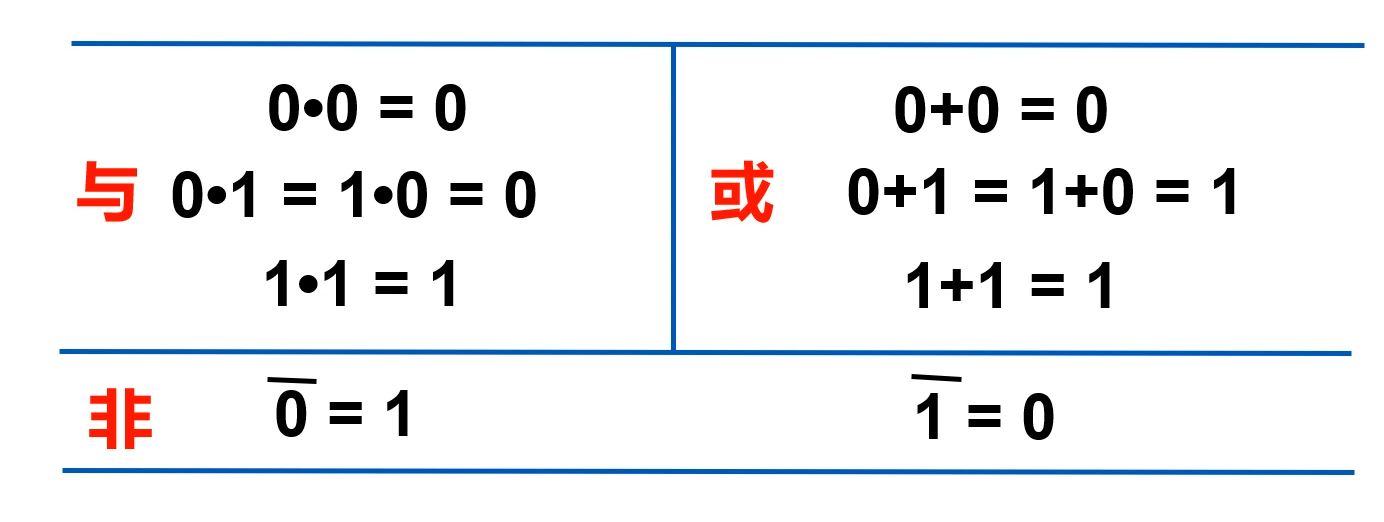
逻辑变量的取值只有0和1,根据三种基本运算的定义,可推得以下关系式
- 0-1律:任何一个逻辑变量和0相与结果都是0,任何一个逻辑变量和0相或结果都是1.
- 自等律:任何一个逻辑变量和1相与结果都是它的本身,任何一个逻辑变量和0相或结果都是它的本身.
- 重叠律:任何一个逻辑变量和它自身相与(相或)结果都是它的本身。
- 互补律:任何一个逻辑变量和它自身的反变量相与结果都是0,任何一个逻辑变量和它自身的反变量相或结果都是1。

2. 和普通代数相似的定律
- 交换律:两个变量相与(相或),互换变量的位置,结果不变。跟小学的加法交换律和乘法交换律是一样的。

- 结合律:三个数相与(相或),先与(或)前两个数,或者先与(或)后两个数,结果不变。跟小学的乘法交换律是一样的。

- 分配率:
把两个数 相或 的结果也就是 B+C
最后和一个数 相与 A·(B+C)
产生的结果等于=
A跟BC 分别 相与 A·B A·C,
分别 相与 的结果 最后再 相或起来 A·B+A·C,
产生的结果是一样的。
A·(B+C)=A·B+A·C
这个跟小学的乘法分配率是一样的

那么反过来
把两个数 相与 也就是B·C
最后和一个数 相或 A+B·C
产生的结果等于=
数A跟两个变量BC 分别相或 A+B A+C,
分别相或 的结果最后再相与起来(A+B)·(A+C),
产生的结果是一样的。
A+B·C=(A+B)·(A+C)

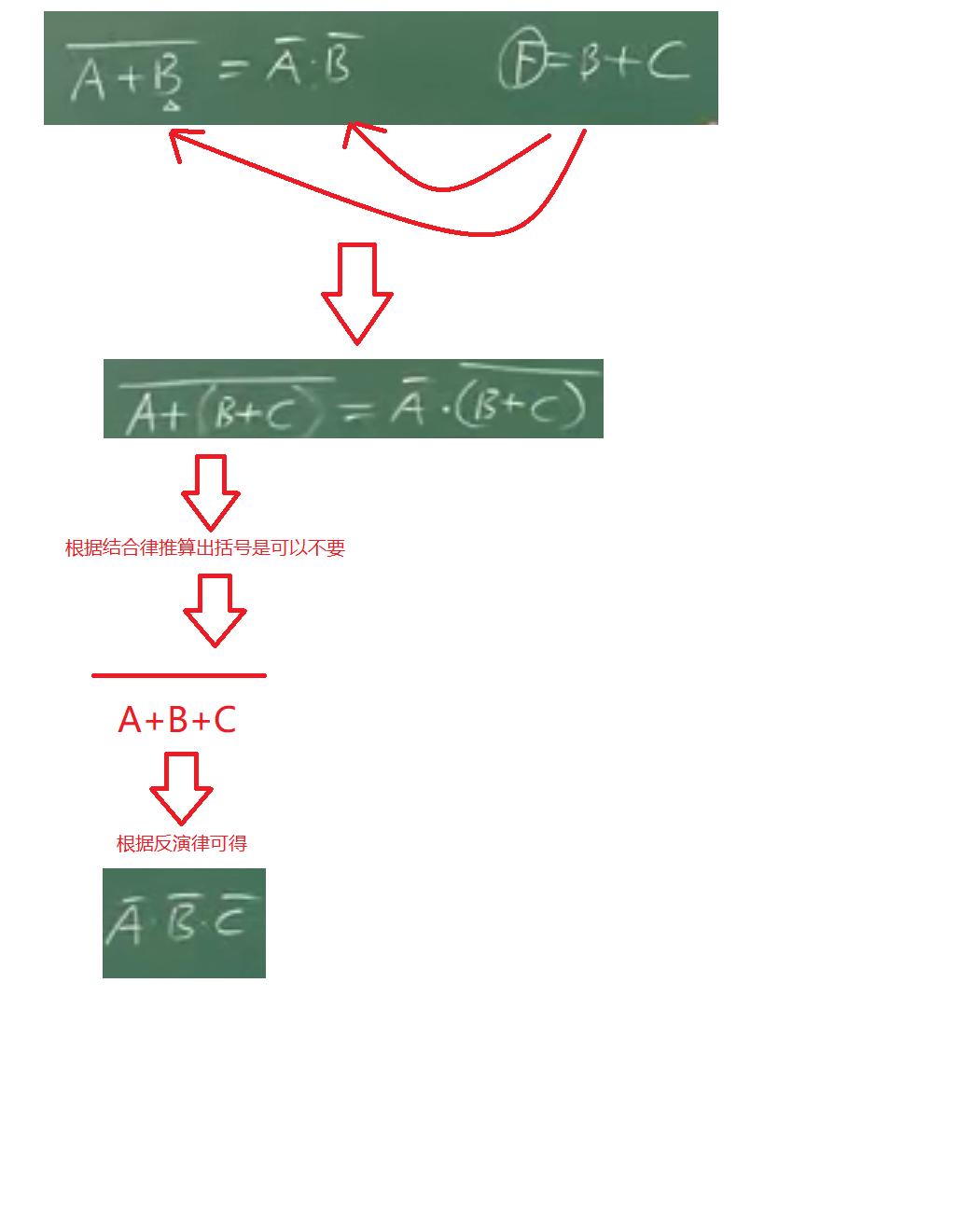
那么在逻辑代数中有着其他不同的基本定律

其中重要的是反演律。
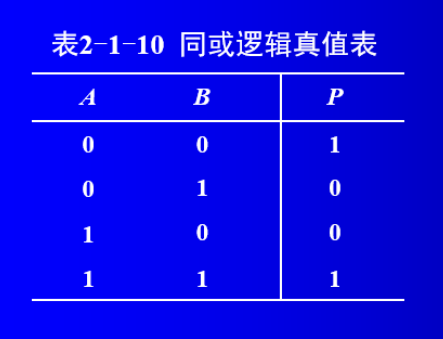
3.常用的异或和同或运算公式

该公式可以通过异或和同或的真值表进行证明

4、其他常用公式
1、合并律

2、吸收律



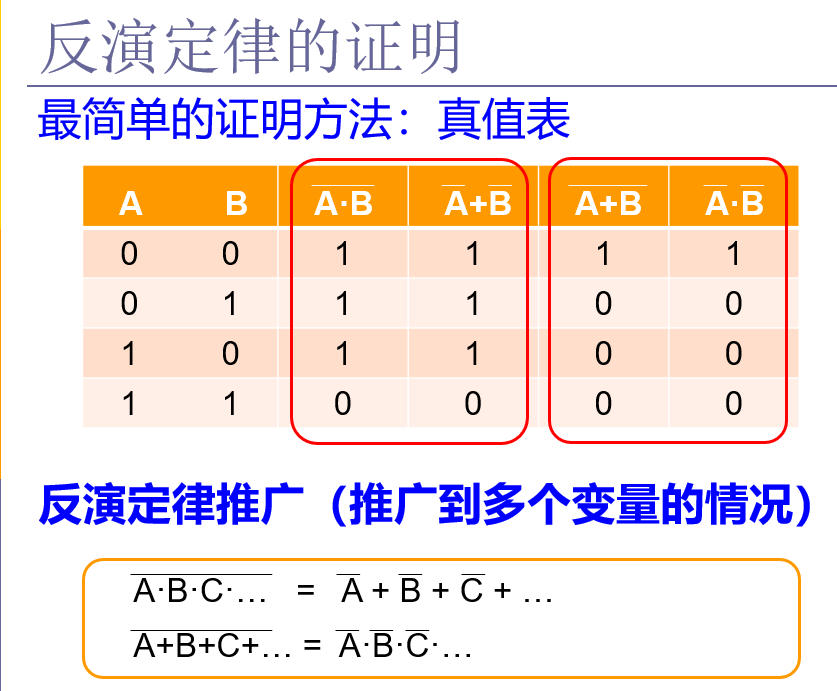
二、定律的证明
1、方法1
要想证明两个式子相等,在逻辑代数里最简单的办法就是罗列出所有的可能性,使用真值表的方式来证明。较为常用。
2、方法2
使用逻辑代数公理的方法来证明


三、逻辑代数三个重要规则
1、规则一,代入规则
代入规则:任何一个逻辑等式,如果将等式两边所出现的某一变量都代之以同一逻辑函数,则等式仍然成立,这个规则称为代入规则。
该例子推导出了代入规则,并将其化简。
2、规则二,反演规则

使用反演规则主要目的就是求出函数的反函数。
例子


3、规则三,对偶规则



四、逻辑运算符的完备性


1、使用“与非门”进行推导“与”“或”“非”
根据上面的结论,发现与非门是一个具有最好完备性,使用与非门能够推倒出“与”“或”“非”。
1.1、使用“与非门”进行推导出“非”
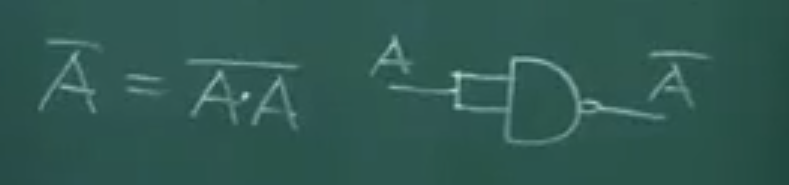
1.2、使用“与非门”进行推导出“与”

1.3、使用“与非门”进行推导出“或”
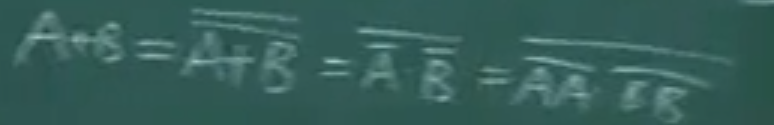
五、逻辑表达式的五种标准形式


六、最大项和最小项
使用最大项和最小项能够证明上面的五种形式函数可以互相转换。
1、最小项

n个变量的积也就是与。ABC三个变量组成的函数,每一个变量都以原变量或者反变量出现一次,也只能出现一次,并且相与。
简单来说最小项就是变量只有与非的表达式,3变量的与非表达式能够组合出8种不同的形式。它们的特点是8种不同的与非表达式,输入同样的变量取值,如:000,最后只有一种表达式会得1,其余得0,所以叫做最小项。
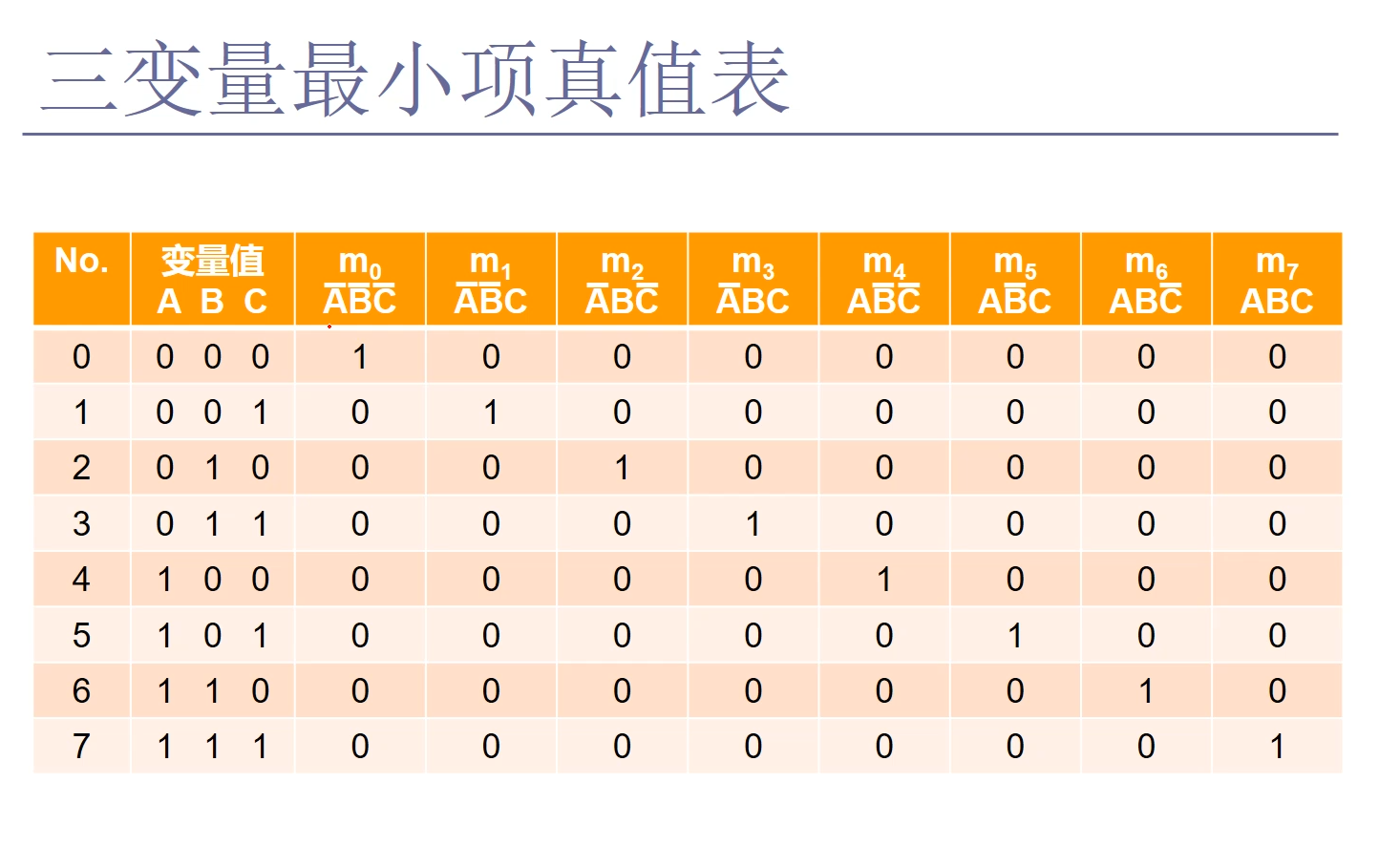
从取值看,变量值为000时得1的最小项,我们可以从这里开始给它编号为0,也就是m0编号最小项。其他编号最小项以此类推。以后为了简写,我们可以用小m0—小m7这些编号来代表不同的最小项。

2、最大项

n个变量的和也就是或。ABC三个变量组成的函数,每一个变量都以原变量或者反变量出现一次,也只能出现一次,并且相或。
简单来说最大项就是变量只有或非的表达式,3变量的或非表达式能够组合出8种不同的形式。它们的特点是8种不同的或非表达式,输入同样的变量取值,如:000,最后只有一种表达式会得0,其余得1,所以叫做最大项。

从取值看,变量值为000时得0的最大项,我们可以从这里开始给它编号为0,也就是M0编号最大项。其他编号最大项以此类推。以后为了简写,我们可以用大M0—大M7这些编号来代表不同的最大项。

3、最大项和最小项的关系
在真值表上,对于最小项来说我们取它变量取值为1的表达式作为编号。
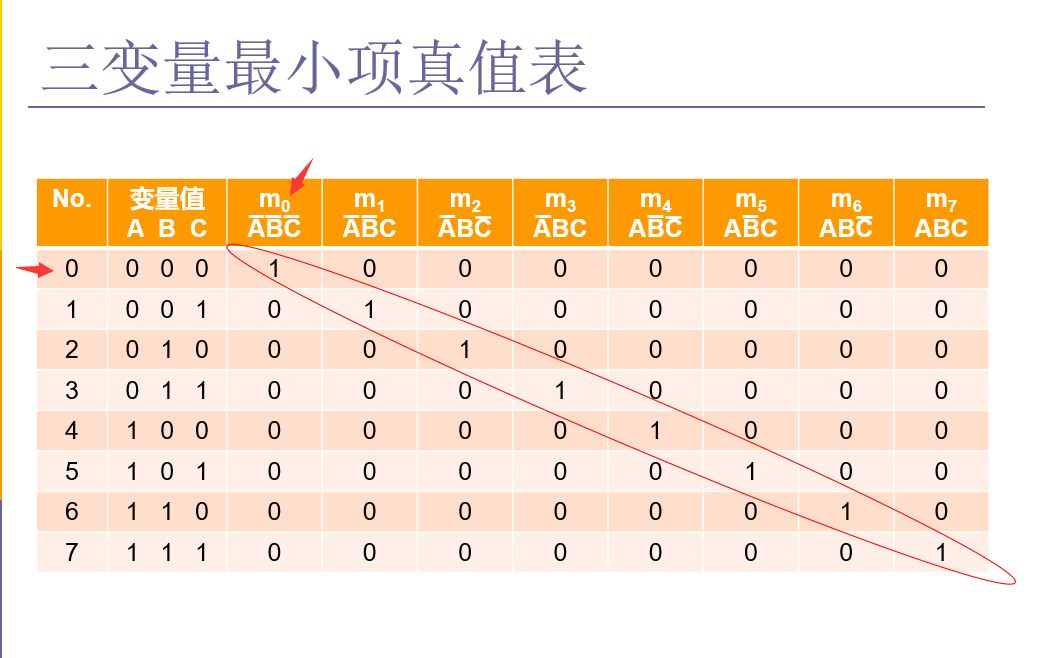
在真值表上,对于最大项来说我们取它变量取值为0的表达式作为编号。
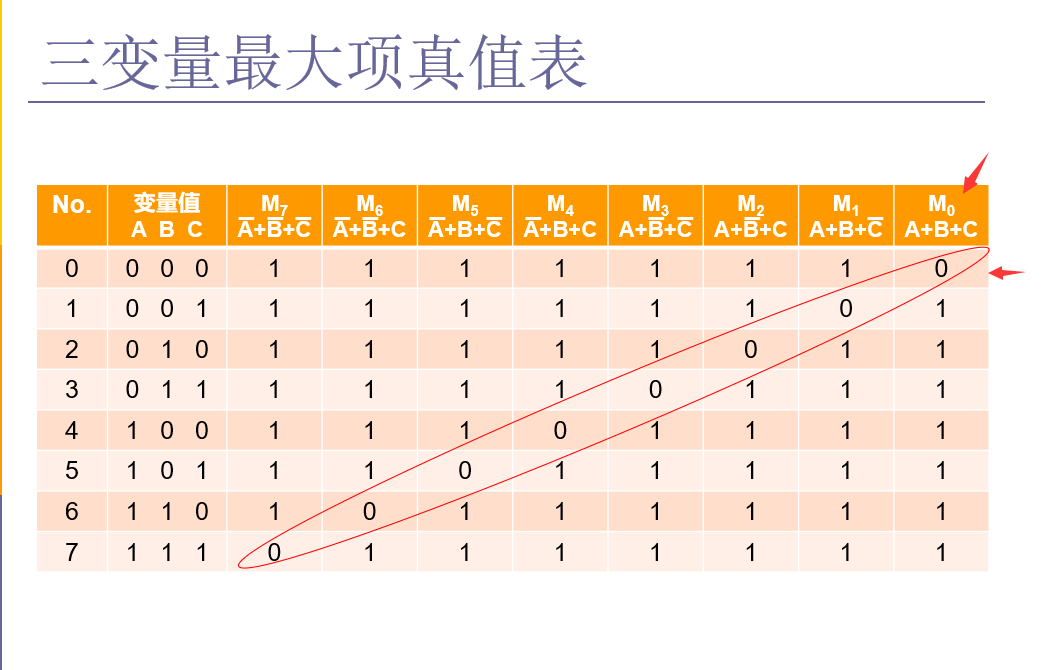
由此可见

4、使用最大项和最小项来表示逻辑函数
有了最大项和最小项的定义之后,就可以用这个来表示逻辑函数。用最大项和最小项表示的逻辑函数就是标准表达式。
4.1、标准表达式1:最小项之和式

使用最小项之和式的目的就是,求出某个函数在什么状态下会得1。由上可见F会在三种情况下取值为1。

由上可见F会四种情况下取值为1。
4.2、标准表达式2:最大项之积式

使用最大项之积式的目的就是,求出某个函数在什么状态下会得0。由上可见F会在4种情况下取值为0。
4.3、由真值表写逻辑表达式
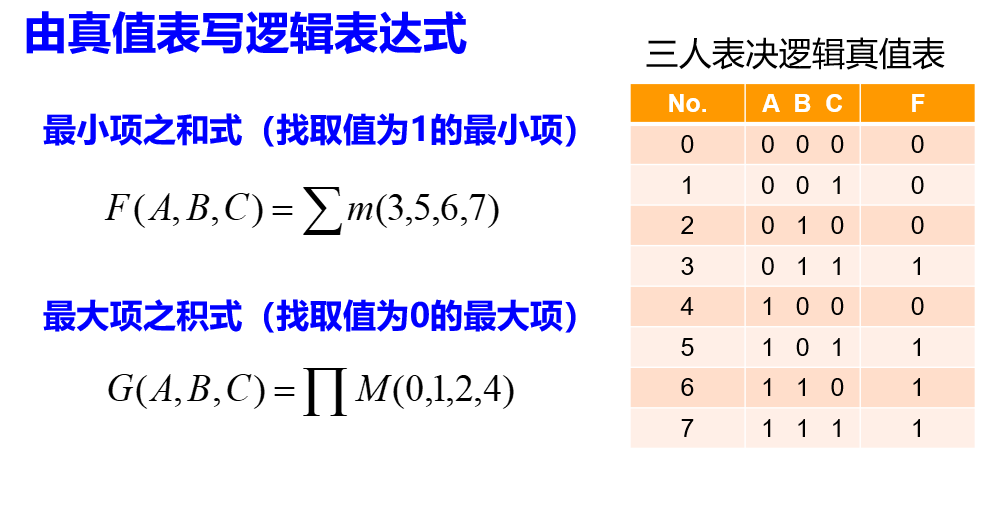

4.4、反函数的标准表达式



