4、逻辑代数

一、逻辑代数概述

逻辑代数是分析和设计逻辑电路的基本数学工具。逻辑代数是英国数学家乔治·布尔于19世纪中叶创立的，因此也叫布尔代数。当时，这种代数纯粹是一种数学游戏，没有任何物理与现实意义。直到20世纪30年代，美国数学家香农在开关电路中找到了它的应用价值，其很快成为分析和设计开关电路的重要数学工具，故又称为开关代数。

在逻辑代数中，参与逻辑运算的变量用字母A、B....表示，称为逻辑变量。每个变量的取值不是0就是1。0和1不表示数值的大小，而是代表两种不同的逻辑状态。

每个事物总有它对立的两个方面，如：“快”的对立面就是“慢”、“大”的对立面是“小”。像这样类似的事物对立的方面称为：事物的二值性

而不同事物之间的状态，会有不同的因果关系，比如：事件A的状态可能会影响事件B的状态。比如说：一个开关的开关闭合可能会影响的灯泡的亮与灭。

最基本的逻辑关系有：与、或、非，三种逻辑关系。

二、基本及常用的逻辑运算

1、”与“逻辑关系

1.1 概念

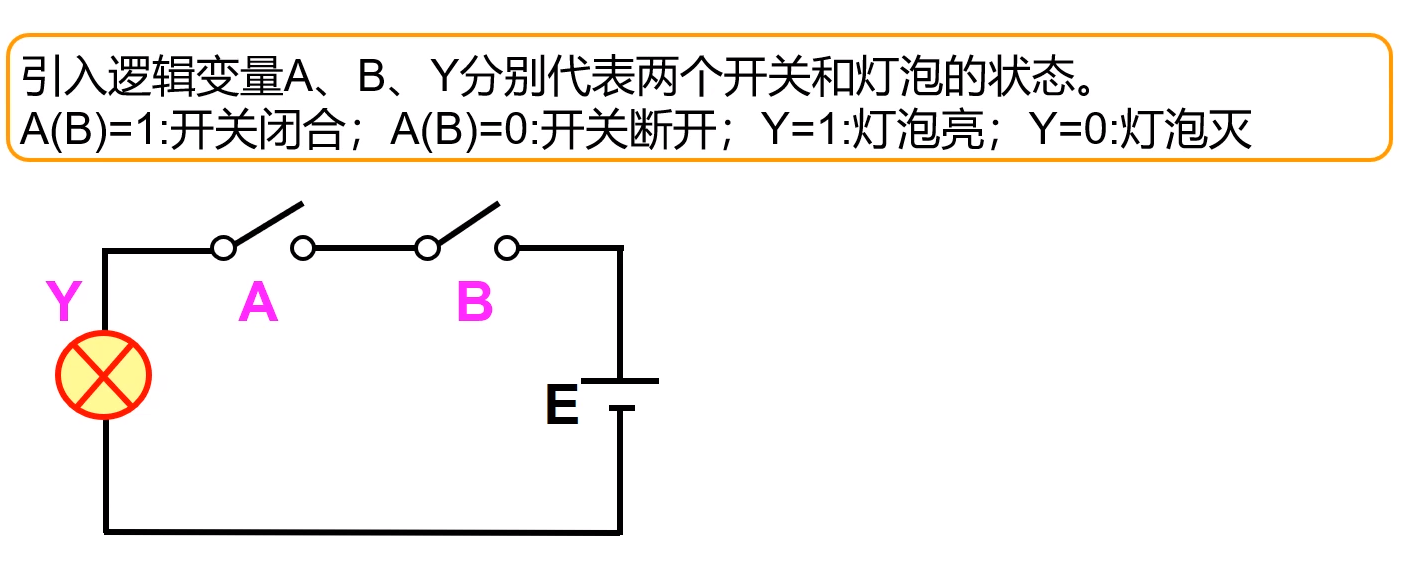
当决定事件的各个条件全部具备之后，事件才会发生。这样的因果关系称为”与“逻辑关系。

如：在电路中只有A和B两个开关都闭合了，灯才会亮。

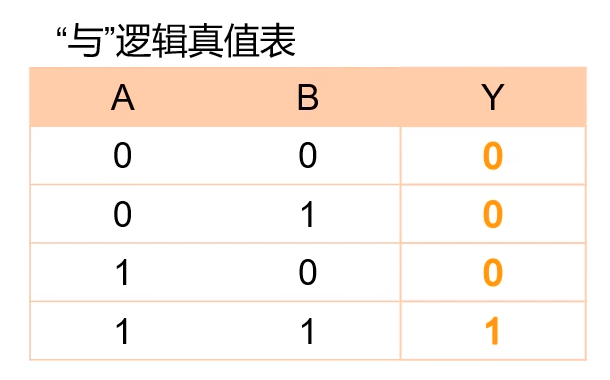
1.2 与逻辑表示真值表

如果用变量A和B分别表示决定这件事情发生的两个条件，用Y表示这件事情的结果，则A、B和Y的与逻辑关系就如表所示，用状态变量和取值可以列出表示三种基本逻辑关系的图表，称为逻辑真值表，或简称真值表。

1.3 ”与“逻辑数学表达式描述法

当状态变量比较多时，使用真值表的列举就不方便了，这个时候就使用到了表达式的方法。

以下是与逻辑不同的数学表达式，它们都是等价的，标注蓝色的表达式是我们常用的。在逻辑代数中，我们又称逻辑与运算也叫做逻辑乘法运算。

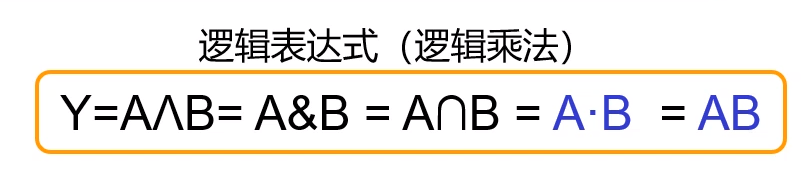
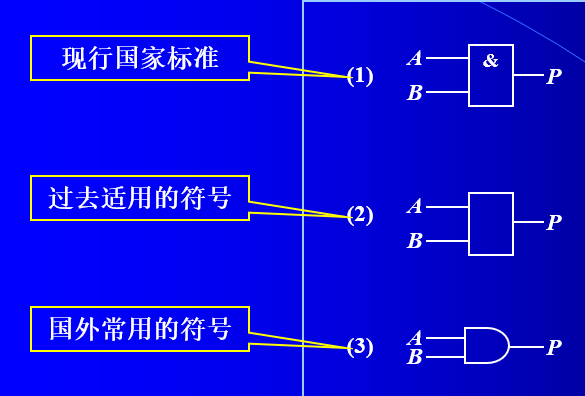
1.4 ”与“逻辑符号描述法

2、”或“逻辑关系

2.1 概念

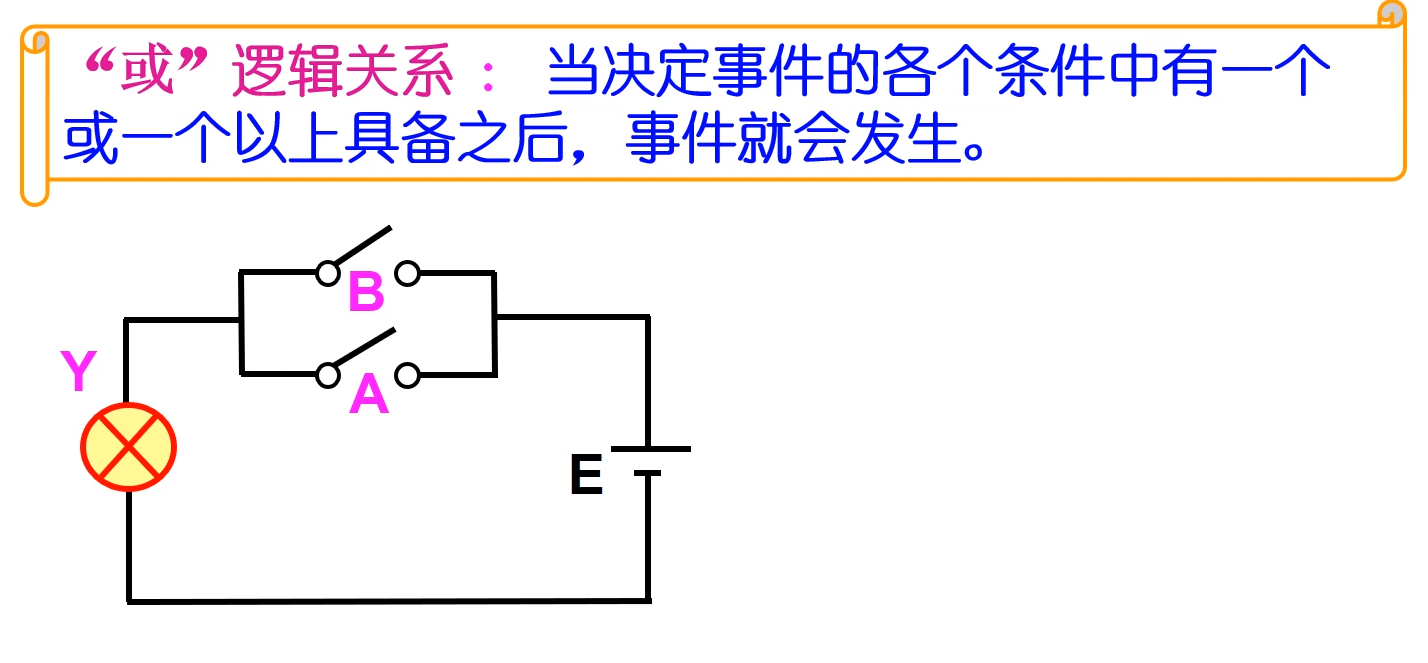
当决定事件的各个条件中有一个或一个以上具备之后，事件就会发生。这样的因果关系称为”或“逻辑关系。

如：在并联电路中，A和B两个开关只要有一个闭合了，灯就会亮。

2.2 ”或“逻辑表示真值表

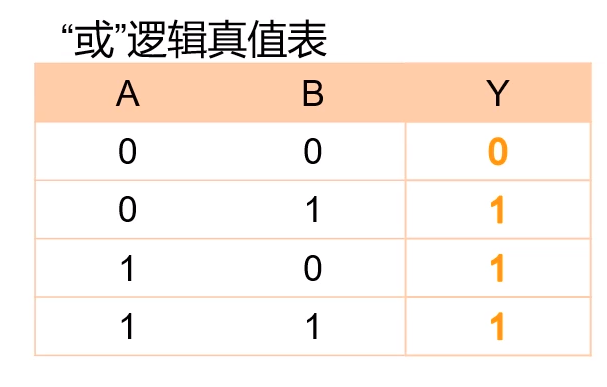
2.3 ”或“逻辑数学表达式描述法

”或“逻辑运算，也称之为逻辑加法。

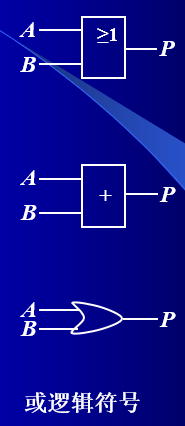
2.4 ”或“逻辑符号表示法

3、 “非”逻辑关系

3.1 概念

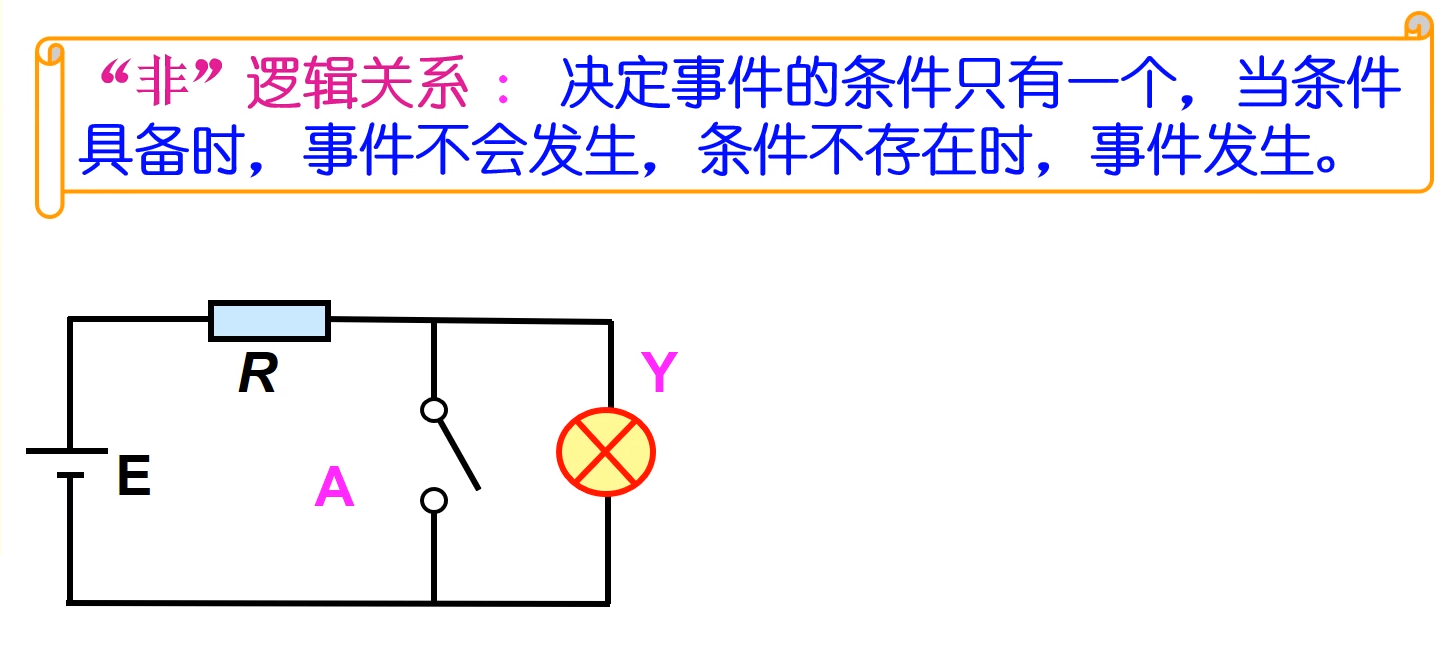
决定事件的条件只有一个，当条件具备时，事件不会发生，条件不存在时，事件发生。这样的因果关系称为”非“逻辑关系。

如：在电路中，A开关只要闭合导致了电路短路，灯就不会亮。

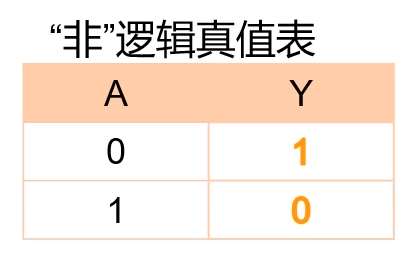
3.2 ”非“逻辑表示真值表

3.3 ”非“逻辑数学表达式描述法

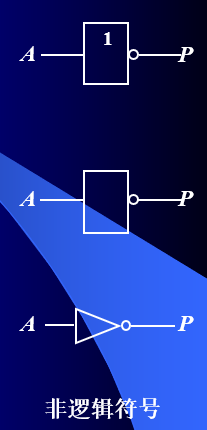
3.4 ”非“逻辑符号表示法

4、波形图—逻辑运算的另一种表示法

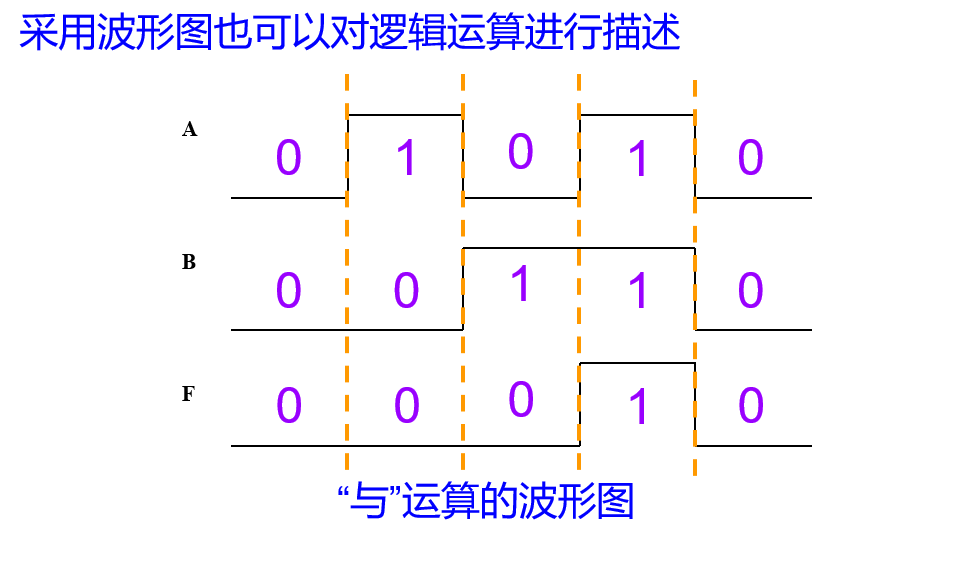
5、逻辑运算的优先次序

6、逻辑函数

逻辑函数：把“与”、“或”、“非”三种基本逻辑运算组合成逻辑表达式，并将该逻辑表达式的运算结果赋予另外一个逻辑变量。

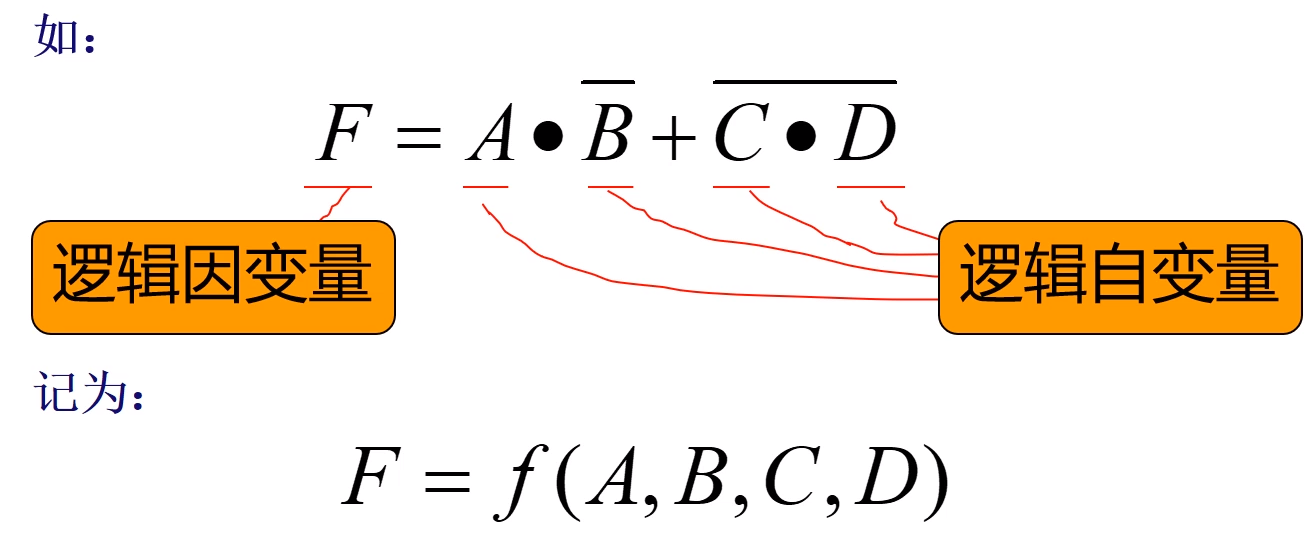
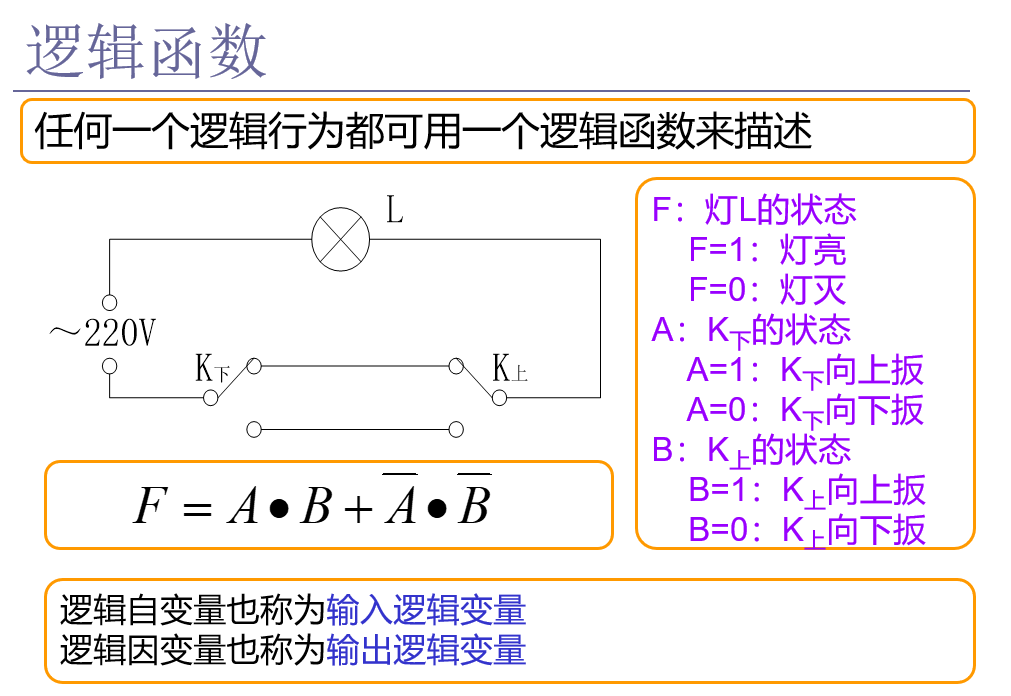
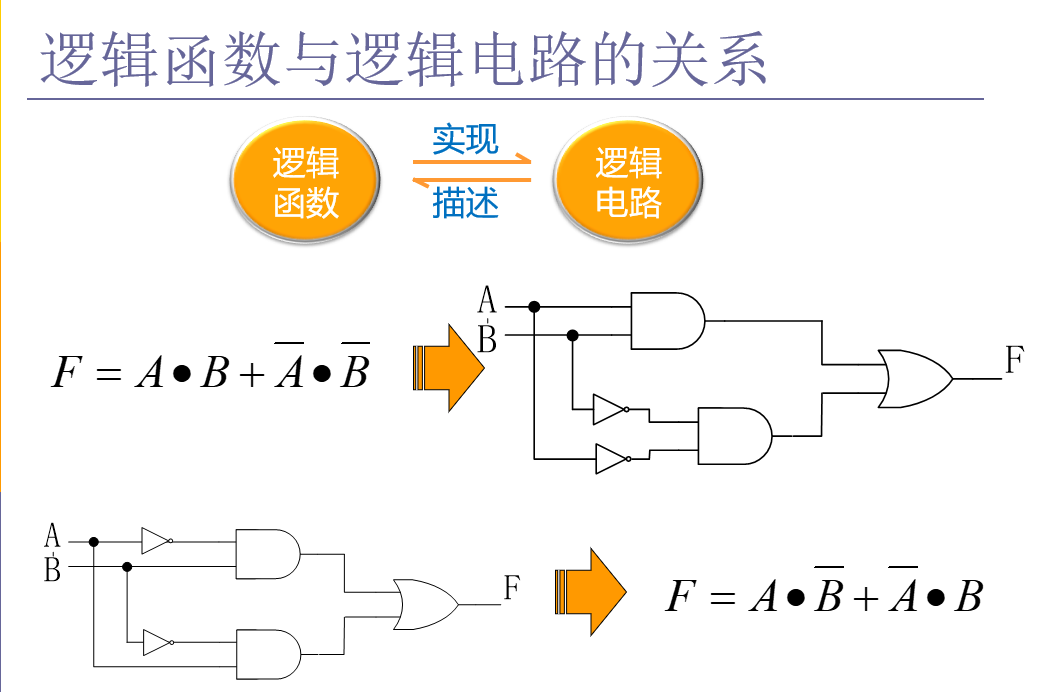
三、复合运算和复合逻辑门

概念

复合运算：将三种基本运算（与、或、非）按某种形式进行的简单的组合构成的新的逻辑运算 。

复合逻辑门：用于实现复合逻辑运算的逻辑门电路，简称复合门。

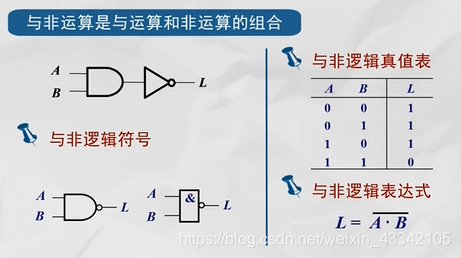
1、”与非“运算

与非运算是将与运算和非运算相结合出来的复合运算，先将变量进行与运算，最后结果再取反。

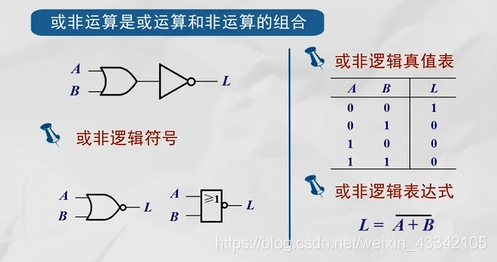
2、”或非“运算

或非运算是将或运算和非运算相结合出来的复合运算，先将变量进行或运算，最后结果再取反。

3、”异或“运算

异或运算，两个变量相同出0，不同出1.

4、”同或“运算

同或运算，两个变量相同出1，不同出0.

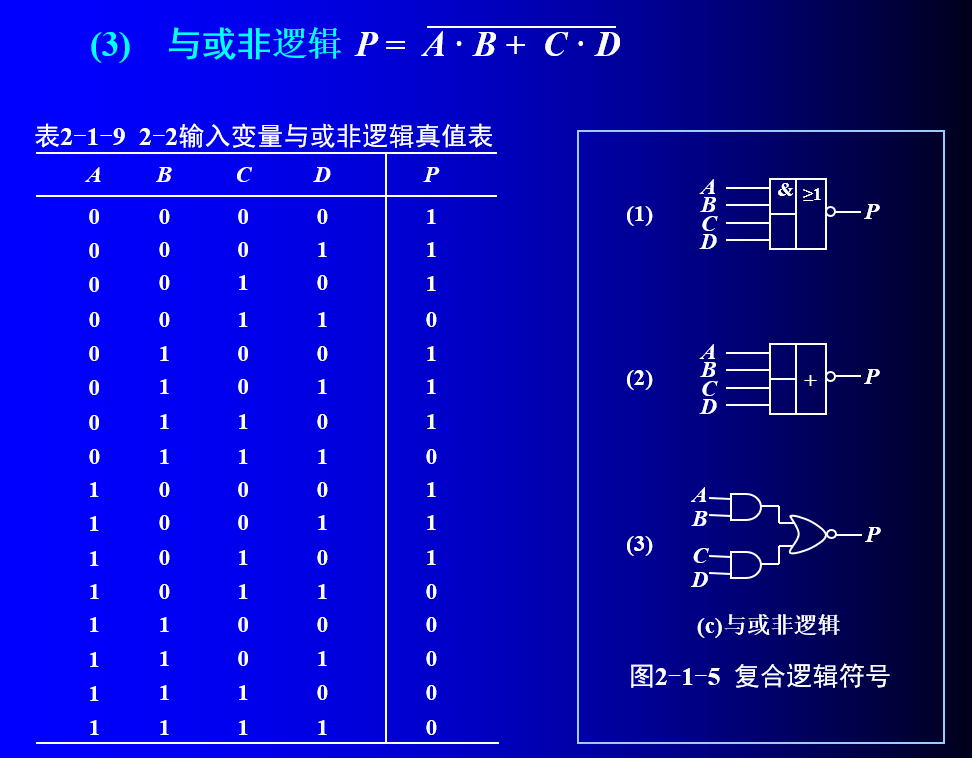
5、”与或非“运算

”与或非“运算，是先进行与运算，再进行或运算，最后进行非运算。