3、带符号的二进制数（原码、反码、补码）

1、数值的符号

​ 之前所提到的二进制数，没有考虑到符号问题，所指的都是无符号数。但实际上数字是有正、负符号的。

​ 以数字6为例，按照习惯的数学表示方法，正数6用+6表示，二进制为+110；负数6用-6表示，二进制数为-110.但在数字系统中，符号“+”、“-”也要数字化，一般将所对应的二进制数最高位增加多一位用来设为符号位，用“0”表示“+”、用“1”表示“-”。

为了区分一个符号数的“+”、“-”符号数字化前后的两种表示方法，引入真值和机器数两个术语。

真值：在一个二进制数前面用“+”、“-”表示正、负数的这种二进制数叫做真值。

机器数：将“+”、“-”符号用二进制码“0”、“1”表示的二进制数叫做机器数。数据最后存到计算机中就是用机器数来表示的

如下：

​ +6 -> +110 -> 0110
​ -6 -> -110 -> 1110
(十进制数) （真值） （机器数）

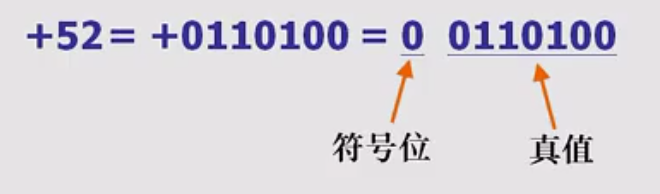
在计算机中最小基本的计算单位是字节，1字节=8位二进制数，由此可见最后存放到计算机中的机器数是8位二进制数，不够补0，符号位占据了1一个位置，所以到了最后只有7位数可以使用。

在c语言中使用 unsigned 关键字可以定义一个无符号的变量，可将变量的存储范围变大。

机器数是由符号位+二进制数组成的，机器数实际上是个大概念，意指这种类型的数据能存进去计算机，机器数在计算机中又有三种不同的表示方法，分别是：原码、补码、反码。下面逐个列举

2、原码

将二进制数的真值中的正符号用0表示，负数符号用1表示，叫做数原码形式，简称原码。

例如：十进制为9的数，它的真值形式和原码形式如下所示：

​ +9 -> +0001001 -> 0 0001001
​ -9 -> - 0001001 -> 1 0001001
(十进制数) （真值） （原码）

原码用8位数码表示，最高位为符号位。

原码的优点是易于辨认，因为它的数值部分就是该数的绝对值，而且与真值和十进制数的转换十分方便。但是在采用原码进行计算时，运算比较是复杂的。

在计算机中加法和减法是最基本的运算，计算机时时刻刻都离不开它们，所以它们由硬件直接支持。为了提高加减法的运算效率，硬件电路要设计得尽量简单。

在使用原码进行加减运算时，会出现这样的情况，当两个数相加时，如果符号是相同的，则两个数值使用加法器直接相加；如果符号位不同时，则要进行减法运算，而且要用减法器来进行减法运算，

对于有符号数，内存要区分符号位和数值位，对于人脑来说，很容易辨别，但是对于计算机来说，就要设计专门的电路，这无疑增加了硬件的复杂性，增加了计算的时间。要是能把符号位和数值位等同起来，让它们一起参与运算，不再加以区分，只用加法器进行运算，这样硬件电路就变得简单了。

为了减少硬件设备量，就引进了反码和补码的数值表示法。

3、反码

加法和减法也可以合并为一种运算，就是加法运算，因为减去一个数相当于加上这个数的相反数，例如，5 - 3 等价于 5 + (-3)，10 - (-9) 等价于 10 + 9。

相反数是指数值相同，符号不同的两个数，例如，10 和 -10 就是一对相反数，-98 和 98 也是一对相反数。

如果能够实现上面的两个目标，那么只要设计一种简单的、不用区分符号位和数值位的加法电路，就能同时实现加法和减法运算，并且非常高效。实际上，这两个目标都已经实现了，真正的计算机硬件电路就是如此简单。

然而，简化硬件电路是有代价的，这个代价就是有符号数在存储和读取时都要进行转化。

反码是在数码左边加上一个符号位，0代表正数，1代表负数。

对于正数，它的反码就是其原码（原码和反码相同）；负数的反码是将原码中除符号位以外的所有位（数值位）取反，也就是 0 变成 1，1 变成 0。

​ +9 -> +0001001 -> 0 0001001 -> 0 0001001
​ -9 -> - 0001001 -> 1 0001001 -> 1 1110110
(十进制数) （真值） （原码） （反码）

由此可以看出：正数的反码与原码相同，负数的反码为其数码位按位取反。

4、补码

假设 6 和 18 都是 short 类型的，现在我们要计算 6 - 18 的结果，根据运算规则，它等价于 6 + (-18)。

如果采用原码计算，那么运算过程为：

6 - 18 = 6 + (-18)
= [0000 0000 0000 0110]原 + [1000 0000 0001 0010]原
= [1000 0000 0001 1000]原
= -24

直接用原码表示整数，让符号位也参与运算，对于类似上面的减法来说，结果显然是不正确的。

于是人们开始继续探索，不断试错，后来设计出了反码。下面就演示了反码运算的过程：

6 - 18 = 6 + (-18)
= [0000 0000 0000 0110]反 + [1111 1111 1110 1101]反
= [1111 1111 1111 0011]反
= [1000 0000 0000 1100]原
= -12

这样一来，计算结果就正确了。

然而，这样还不算万事大吉，我们不妨将减数和被减数交换一下位置，也就是计算 18 - 6 的结果：

18 - 6 = 18 + (-6)
= [0000 0000 0001 0010]反 + [1111 1111 1111 1001]反
= [1 0000 0000 0000 1011]反
= [0000 0000 0000 1011]反
= [0000 0000 0000 1011]原
= 11

按照反码计算的结果是 11，而真实的结果应该是 12 才对，它们相差了 1。

加粗的 1 是加法运算过程中的进位，它溢出了，内存容纳不了了，所以直接截掉。

6 - 18 的结果正确，18 - 6 的结果就不正确，相差 1。按照反码来计算，是不是小数减去大数正确，大数减去小数就不对了，始终相差 1 呢？我们不妨再看两个例子，分别是 5 - 13 和 13 - 5。

5 - 13 的运算过程为：

5 - 13 = 5 + (-13)
= [0000 0000 0000 0101]原 + [1000 0000 0000 1101]原
= [0000 0000 0000 0101]反 + [1111 1111 1111 0010]反
= [1111 1111 1111 0111]反
= [1000 0000 0000 1000]原
= -8

13 - 5 的运算过程为：

13 - 5 = 13 + (-5)
= [0000 0000 0000 1101]原 + [1000 0000 0000 0101]原
= [0000 0000 0000 1101]反 + [1111 1111 1111 1010]反
= [1 0000 0000 0000 0111]反
= [0000 0000 0000 0111]反
= [0000 0000 0000 0111]原
= 7

这足以证明，刚才的猜想是正确的：小数减去大数不会有问题，而大数减去小数的就不对了，结果始终相差 1。

相差的这个 1 要进行纠正，但是又不能影响小数减去大数，怎么办呢？于是人们又绞尽脑汁设计出了补码，给反码打了一个“补丁”，终于把相差的 1 给纠正过来了。

对于正数，它的补码就是其原码（原码、反码、补码都相同）；负数的补码是其反码加 1。

可以认为，补码是在反码的基础上打了一个补丁，进行了一下修正，所以叫“补码”。

原码、反码、补码的概念只对负数有实际意义，对于正数，它们都一样。

​ +9 -> +0001001 -> 0 0001001 -> 0 0001001 -> 0 0001001
​ -9 -> - 0001001 -> 1 0001001 -> 1 1110110 -> 1 1110111
(十进制数) （真值） （原码） （反码） （补码）

在计算机内存中，整数一律采用补码的形式来存储。这意味着，当读取整数时还要采用逆向的转换，也就是将补码转换为原码。
将补码转换为原码也很简单：先减去 1，再将数值位取反即可。