2、进制详解（整数部分）

概念：什么是进制

• 我们平时使用的数字都是由 0~9 共十个数字组成的，例如 1、9、10、297、952 等，一个数字最多能表示九，如果要表示十、十一、二十九、一百等，就需要多个数字组合起来。
  例如表示 5+8 的结果，一个数字不够，只能”进位“，用 13 来表示；这时”进一位“相当于十，”进两位“相当于二十。

• 因为逢十进一（满十进一），也因为只有 0~9 共十个数字，所以叫做十进制（Decimalism）。十进制是在人类社会发展过程中自然形成的，它符合人们的思维习惯，例如人类有十根手指，也有十根脚趾。

• 学习进制，必须首先掌握数码、基数、位权这三个概念。

  数码:数制中表示基本数值大小的不同数字符号
  例如，十进制有10个数码: 0、1、2、3、4、5、6、7、8、9。

  基数:数制所使用数码的个数
  例如，二进制有两个数码：0、1所以它的基数为2;十进制使用10个数码，它的基数为10。N进制的基数为N

  位权:
  官方说法：数制中某一位上的1所表示数值的大小（数码所处位置的价值）。若某数制的基数为 N，则第i位的位权为基数的i次方（Ni)
  例如，十进制数“795”，其个位数5的位权是100，十位数9的位权是101，百位数7的位权是102。
  通俗说法：
  1、在各种数制（无论是二进制，十进制、十六进制等）中，各位数字所表示值的大小不仅与该数字本身的大小有关，还与该数字所在的位置有关，我们称这关系为数的位权。
  2、拿十进制做个不科学但最通俗的比喻，不能说4一定比2大，还要看它在整个数中的位置。如：40中的4代表的值比200中的2所代表的值要小。

  一个二进制数110，其中高位的1表示1个2x2，即4，低位的1表示1个2x1，即2，最低位的0表示0个2x0，即0。
  可见，在数制中，各位数字所表示值的大小不仅与该数字本身的大小有关，还与该数字所在的位置有关，我们称这关系为数的位权。 二进制数的位权是以2为底的幂...
  所以110按照权展开就是110=2x2x1+2x1x1+2x0x0
  权值=当前数值xN进制的"位置"幂。权位都是从右往左开始的，第一位从0开始。

• 进制也就是进位制。进行加法运算时逢X进一（满X进一），进行减法运算时借一当X，这就是X进制，这种进制也就包含X个数字，基数为X。十进制有 0~9 共10个数字，基数为10，在加减法运算中，逢十进一，借一当十。

  常用的进制有：二进制、八进制、十进制、十六进制。刚刚已经介绍过了十进制，下面来讲解其他进制。

一、常见的进制

1、二进制

用0、1两个数字来表示数值，这就是二进制（Binary）。例如，数字 0、1、10、111、100、1000001 都是有效的二进制。在计算机内部，数据都是以二进制的形式存储的。

2、八进制

八进制有 0~7 共8个数字，例如，数字 0、1、5、7、14、733、67001、25430 都是有效的八进制。

3、十六进制

除了二进制和八进制，十六进制也经常使用，甚至比八进制还要频繁。

十六进制中，用A来表示10，B表示11，C表示12，D表示13，E表示14，F表示15，因此有 0~F 共16个数字，基数为16。例如，数字 0、1、6、9、A、D、F、419、EA32、80A3、BC00 都是有效的十六进制。

注意，十六进制中的字母不区分大小写，ABCDEF 也可以写作 abcdef。

二、进制加减法

1、二进制加减法

二进制加减法和十进制加减法的思想是类似的：

对于十进制，进行加法运算时逢十进一，进行减法运算时借一当十；
对于二进制，进行加法运算时逢二进一，进行减法运算时借一当二。

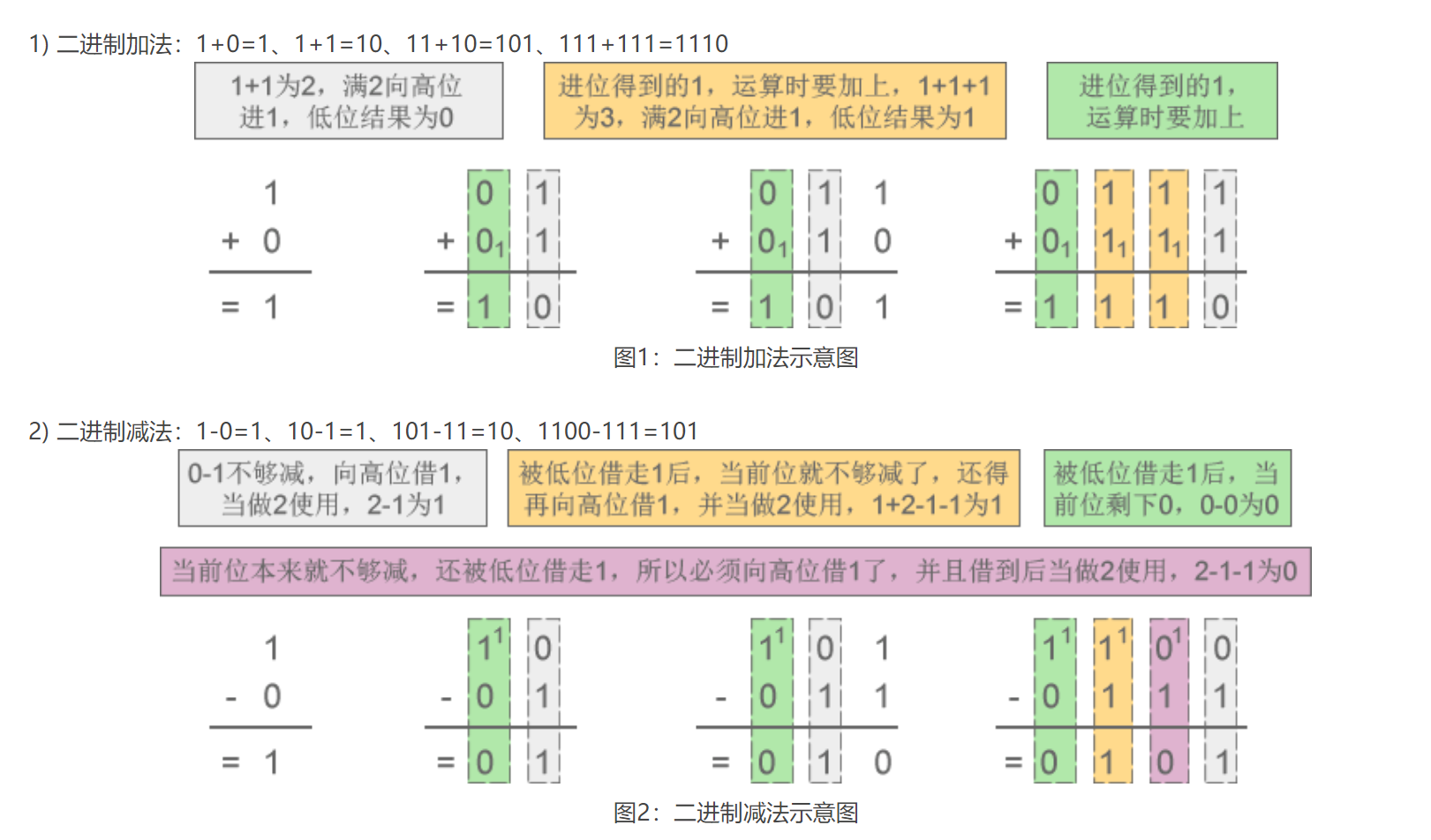
二进制的小数加减法同理

2、八进制加减法

八进制加法运算时逢八进一，减法运算时借一当八。

要点：如果当前位相加满8，向高位进1，然后再减去8，就是当前位的和

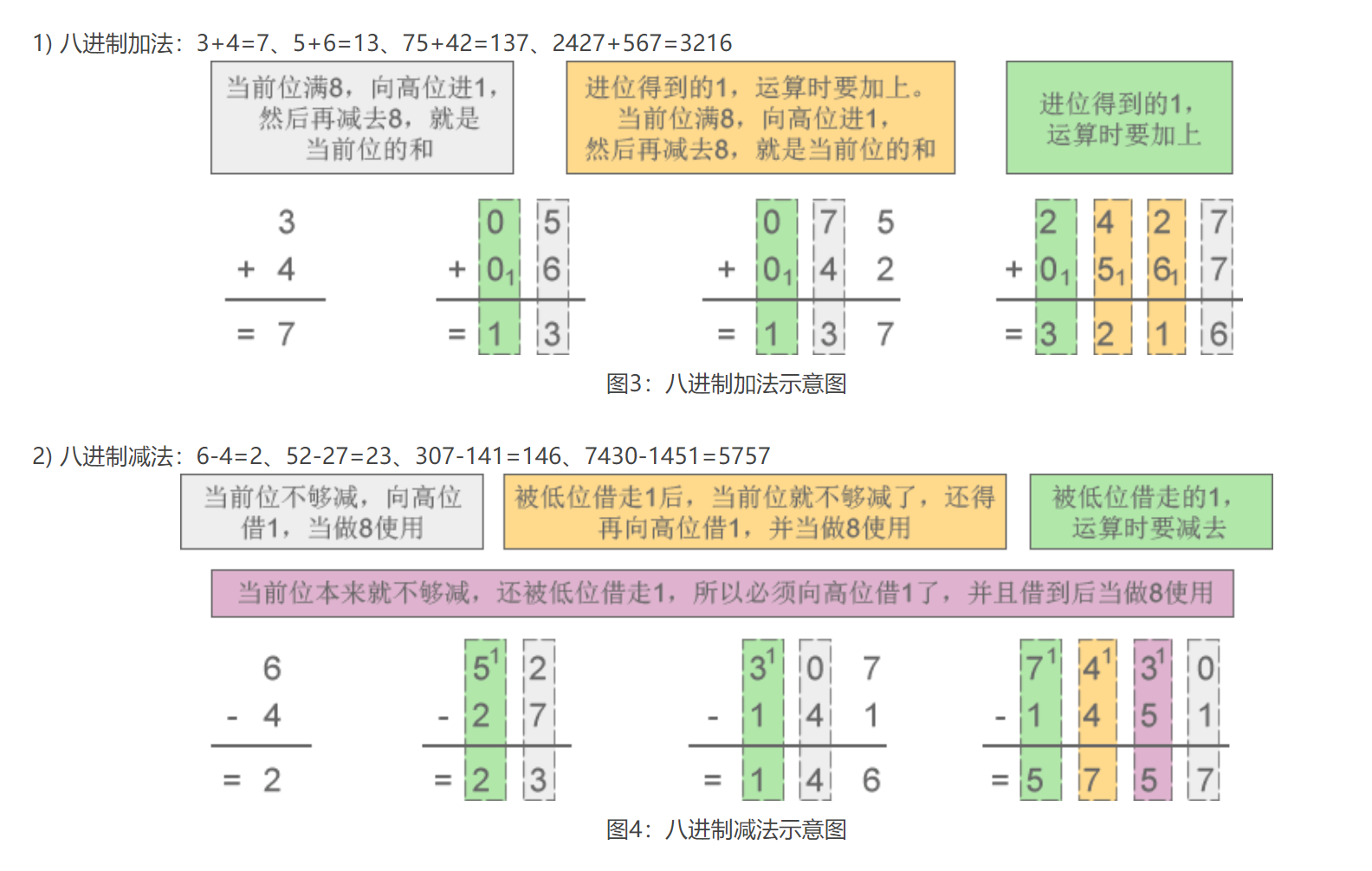
八进制的小数加减法同理

3、十六进制加减法

十六进制加法运算时逢16进1，减法运算时借1当16。

**要点：如果当前位相加满16，向高位进1，然后再减去16，就是当前位的和 **

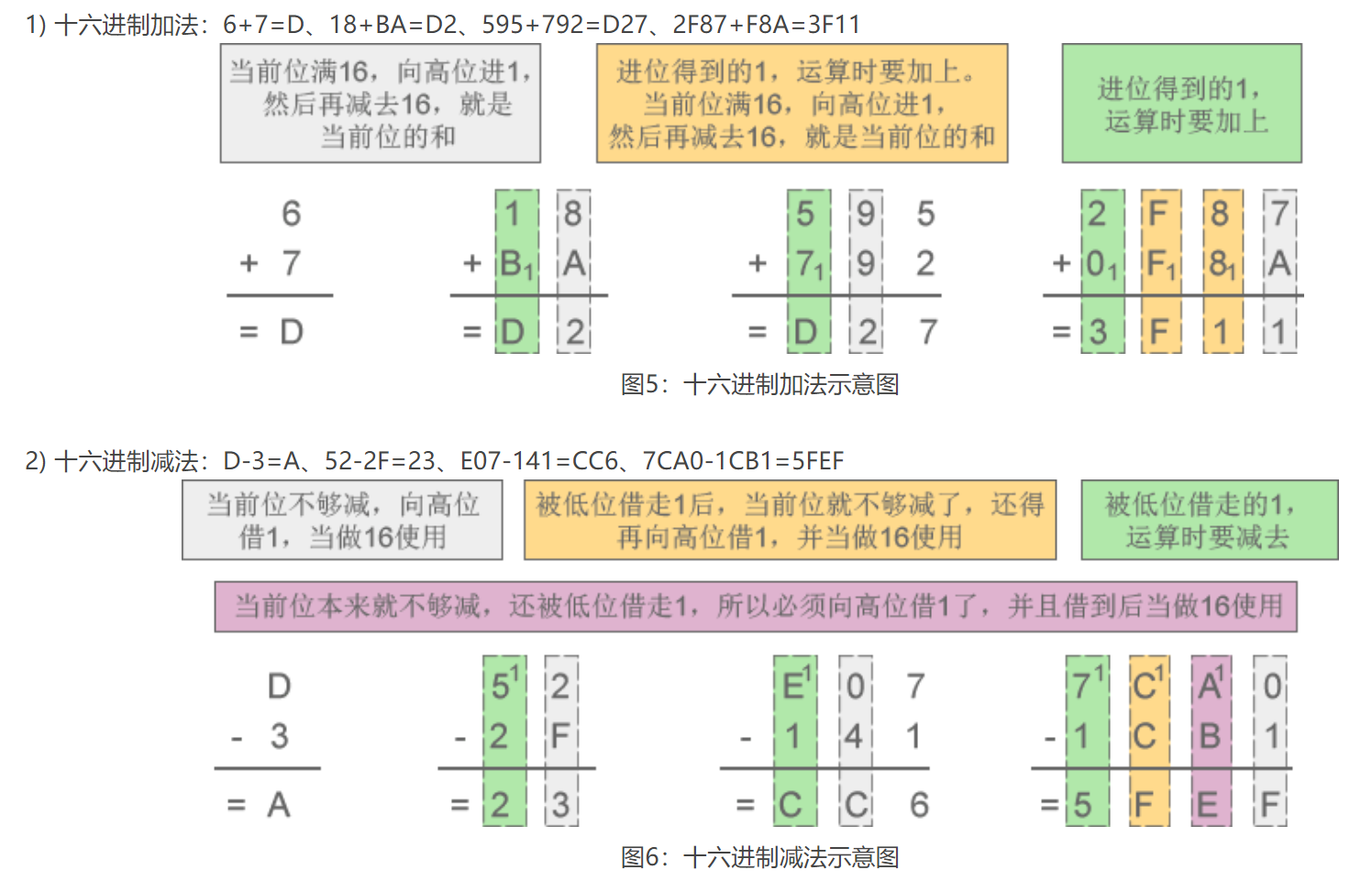
十六进制的小数加减法同理

不同进制之间想要进行加法或者减法，都进行先转换成二进制再进行运算

三、进制转换

1、将二进制、八进制、十六进制转换为十进制

二进制、八进制和十六进制向十进制转换都非常容易，就是“按权相加”。所谓“权”，也即“位权”，第几位数。

注意，这里我们需要以十进制形式来表示位权。

1) 整数部分

将二进制数字转换成十进制

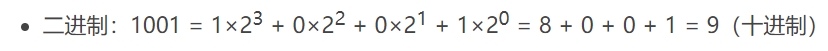
将八进制数字转换成十进制

将十六进制数字转换成十进制

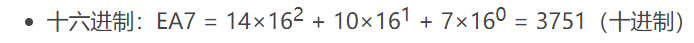
2) 小数部分

将二进制小数转换成十进制

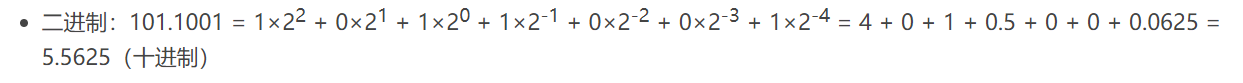
将八进制小数转换成十进制

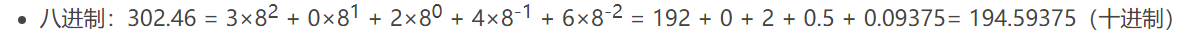
十六进制小数转换成十进制同理。

3) 总结

将N进制转成十进制使用的方法是权位展开。

2、将十进制转换为二进制、八进制、十六进制

将十进制转换为其它进制时比较复杂，整数部分和小数部分的算法不一样，下面我们分别讲解。

1) 整数部分

十进制整数转换为 N 进制整数采用“除 N 取余，逆序排列”法。具体做法是：

• 将 N 作为除数，用十进制整数除以 N，可以得到一个商和余数；
• 保留余数，用商继续除以 N，又得到一个新的商和余数；
• 仍然保留余数，用商继续除以 N，还会得到一个新的商和余数；
• ……
• 如此反复进行，每次都保留余数，用商接着除以 N，直到商为 0 时为止。

把先得到的余数作为 N 进制数的低位数字，后得到的余数作为 N 进制数的高位数字，依次排列起来，就得到了 N 进制数字。

将十进制数字转换成二进制

注意，当被除数为1时，1除以任何数，其余数都是1。

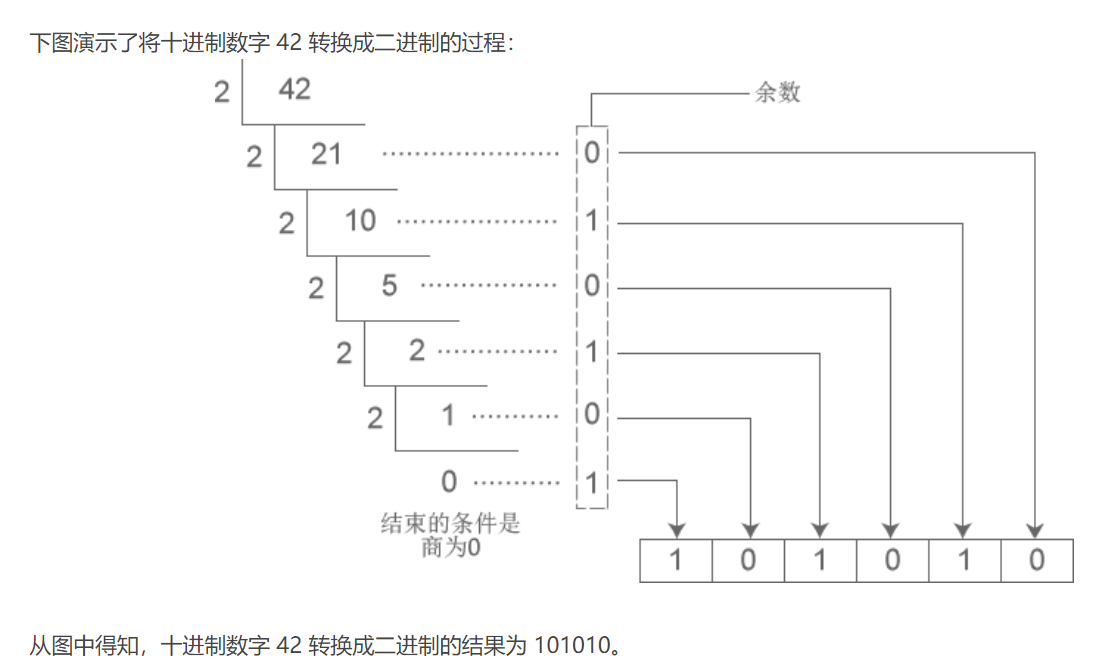
将十进制数字转换成八进制

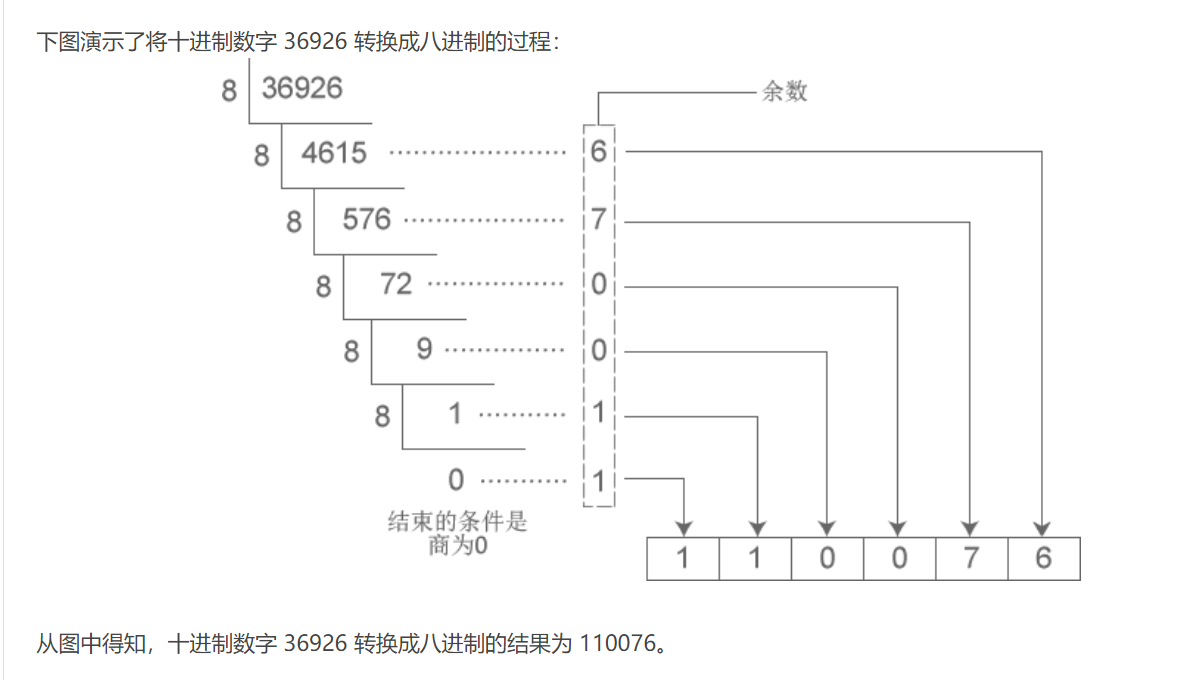
十进制的数字转16进制同理

2) 小数部分

十进制小数转换成 N 进制小数采用“乘 N 取整，顺序排列”法。具体做法是：

• 先将整数与小数进行分离，整数单独进行转换二进制数；
• 用 N 乘以十进制的小数，可以得到一个积，这个积包含了整数部分和小数部分；
• 将积的整数部分取出，再用 N 乘以余下的小数部分，又得到一个新的积；
• 再将积的整数部分取出，继续用 N 乘以余下的小数部分；
• ……
• 如此反复进行，每次都取出整数部分，用 N 接着乘以小数部分，直到积中的小数部分为 0，或者发现该操作会无限循环，那么达到所要求的精度为止。

把取出的整数部分按顺序排列起来，先取出的整数作为 N 进制小数的高位数字，后取出的整数作为低位数字，这样就得到了 N 进制小数。

如果一个数字既包含了整数部分又包含了小数部分，那么将整数部分和小数部分开，分别按照上面的方法完成转换，然后再合并在一起即可。例如：

• 十进制数字 36926.930908203125 转换成八进制的结果为 110076.7345；
• 十进制数字 42.6875 转换成二进制的结果为 101010.1011。

将十进制小数转换成二进制

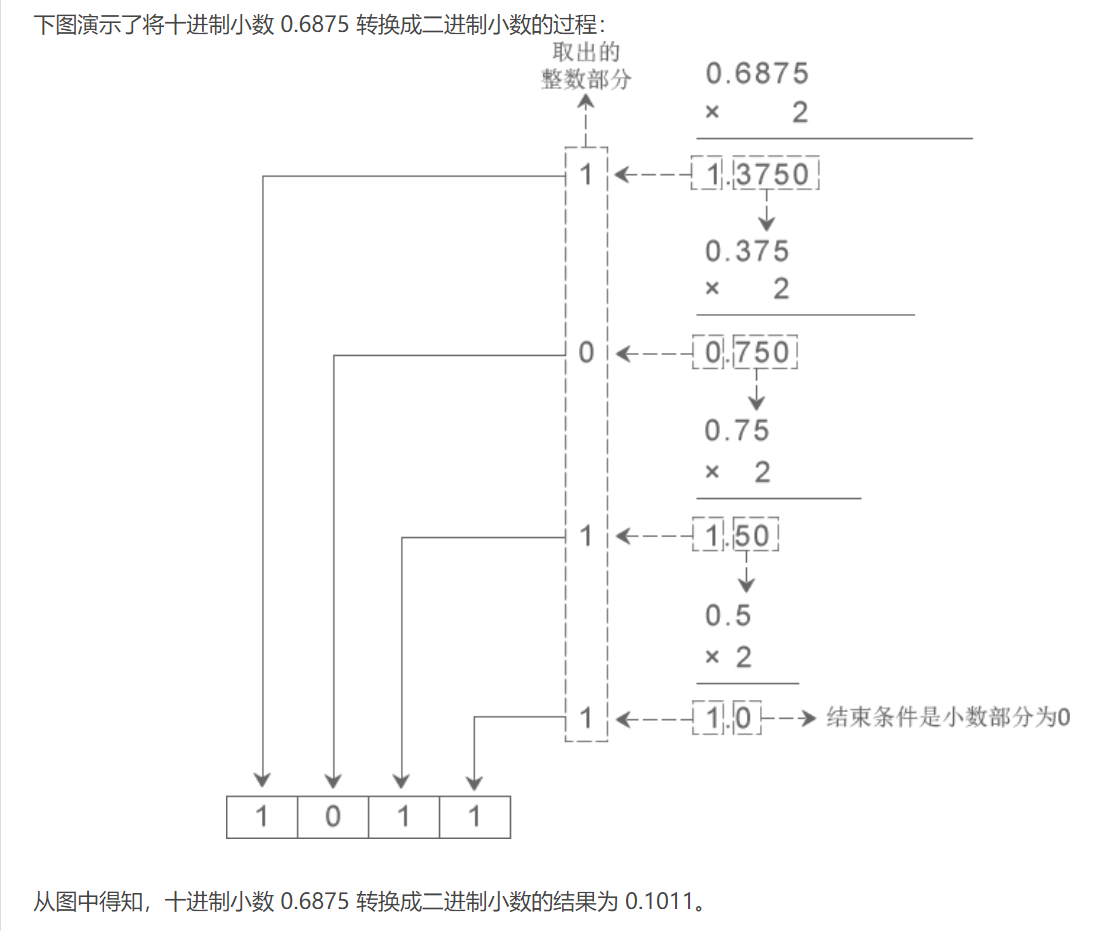
将十进制小数转换成八进制

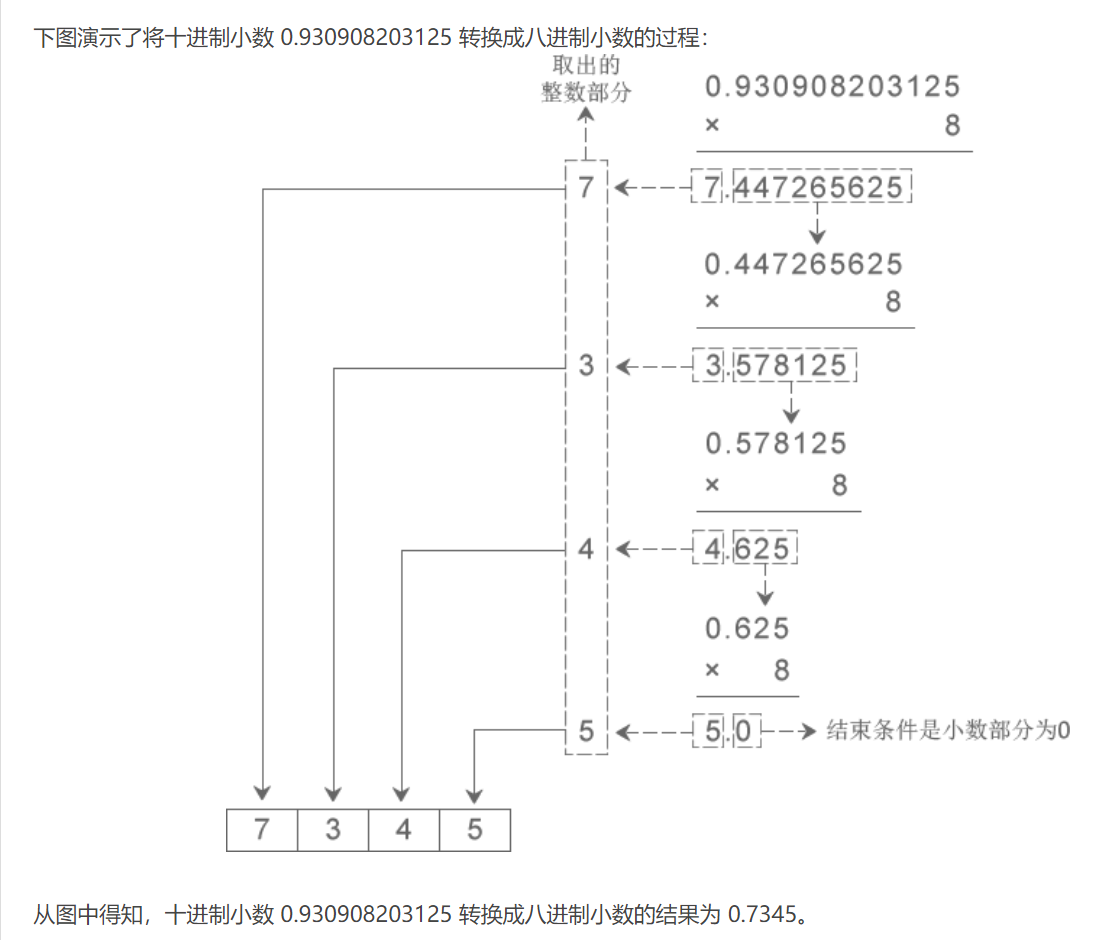
十进制的小数转16进制同理

3、二进制和八进制、十六进制的转换

二进制转换其他进制使用的是权位展开计算法

1) 二进制整数和八进制整数之间的转换

2) 二进制整数和十六进制整数之间的转换

4、总结

• N进制转换十进制使用的是权位展开。
• 十进制转换N进制使用的是除N取余。
• N进制转换Y进制，N进制可以通过进制对照表换算出每一位的二进制数，再通过二进制转换成Y进制。

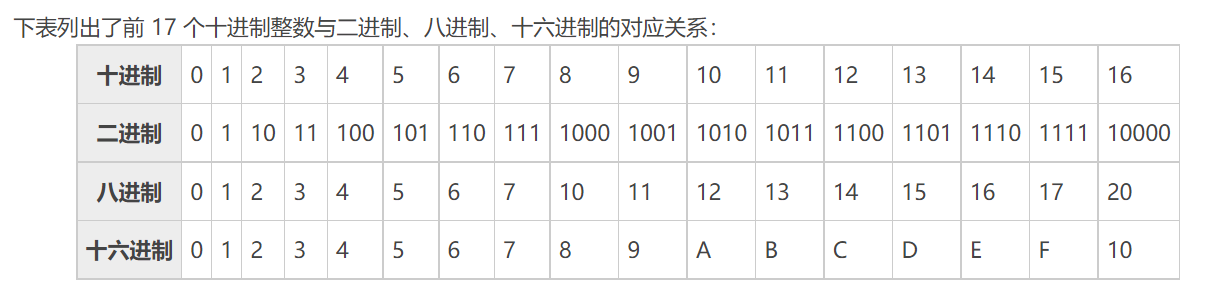
四、进制对应表

五、编码

用代码表示信息的过程称为编码。在数字系统中，由于二进制数用电路实现起来比较容易，因此在编码中广泛使用的是二进制数。我们称用二进制数表示文字符号等信息的过程为二进制编码。
常用的二进制编码方法如下。

1、顺序二进制编码

将十进制数转换成二进制数，所得到的二进制编码就是顺序二进制码，简称二进制码。其特点是相邻的两个数之间的差值为1。

2、独热码

只有一个二进制位为1，其他全为0的编码叫做独热码，又称一位有效编码，其方法是使用N位状态寄存器来对N个状态进行编码，每个状态都有它独立的寄存器位，并且在任意时候，其中只有一位有效。即，只有一位是1，其余都是零值。这中编码方式中，编码的二进制位数与需要进行编码的状态数相等。

例如，对六个状态进行编码：

自然顺序码为 000,001,010,011,100,101
独热编码则是 000001,000010,000100,001000,010000,100000

回到一开始的例子，性别特征：["男","女"]，按照N位状态寄存器来对N个状态进行编码的原理：

性别特征：["男"，"女"]（这里N=2）
男 => 10
女 => 01

地区特征：["北京"，"上海，"深圳"]（这里N=3）：
北京 => 100
上海 => 010
深圳 => 001

工作特征：["演员"，"厨师"，"公务员"，"工程师"，"律师"]（这里N=5）：
演员 => 10000
厨师 => 01000
公务员 => 00100
工程师 => 00010
律师 => 00001

所以，样本的特征是["女","北京","工程师"]的时候，独热编码（One-Hot Encoding）的结果为：

[0，1，1，0，0，0，0，0，1，0]

3、二-十进制编码(BCD码)

• 日常生活中最常使用的是十进制数。在数字系统中，为了既满足系统中使用二进制数的要求，又适应人们使用十进制数的习惯，需要用二进制数来表示十进制数。即用4位二进制数，对十进制数中的10个数符进行编码，简称二-十进制编码，又称BCD码，有了BCD码才有了后来的进制转换。

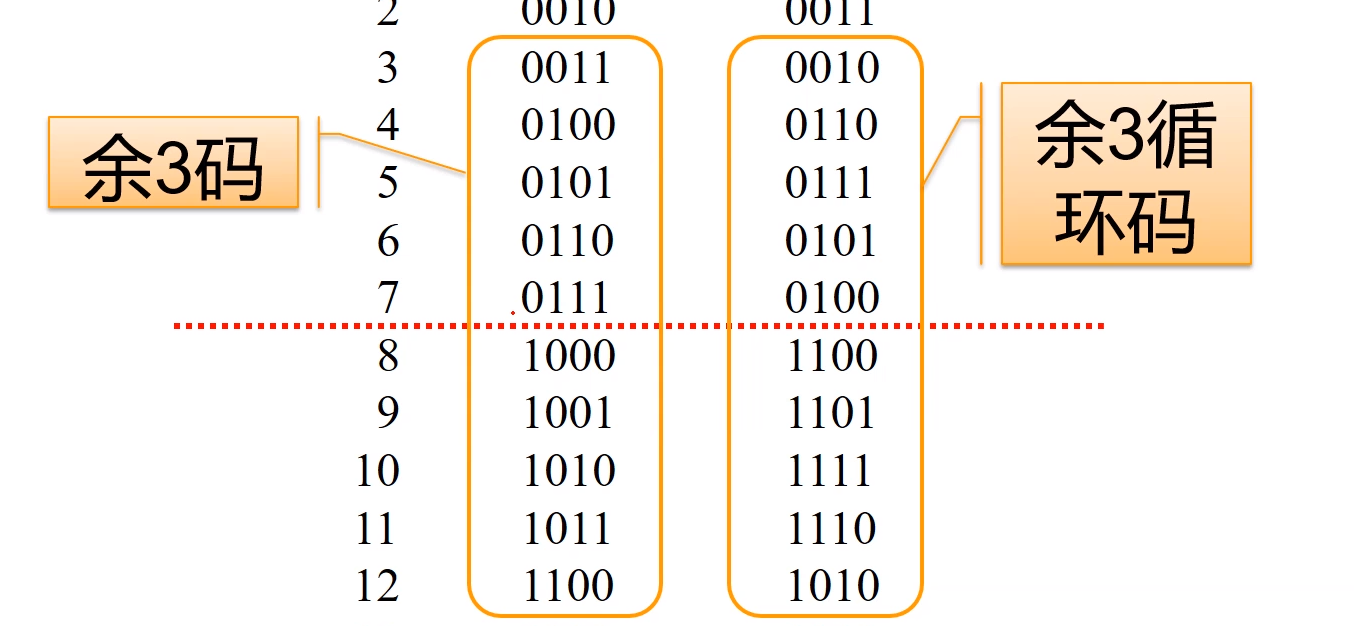
• 二-十进制编码有多种不同的编码方法，也就是说有多种不同的BCD码，常用的有8421码、2421BCD码、5211BCD码、余3码、余3格雷码等。
  

• 使用二进制来表示十进制的话，需要用到4位二进制，但是4位的二进制的组合又能表示出0~15（16个）十进制数。因此需要在二进制的16组合里面取出十个来表示0-9个十进制数。

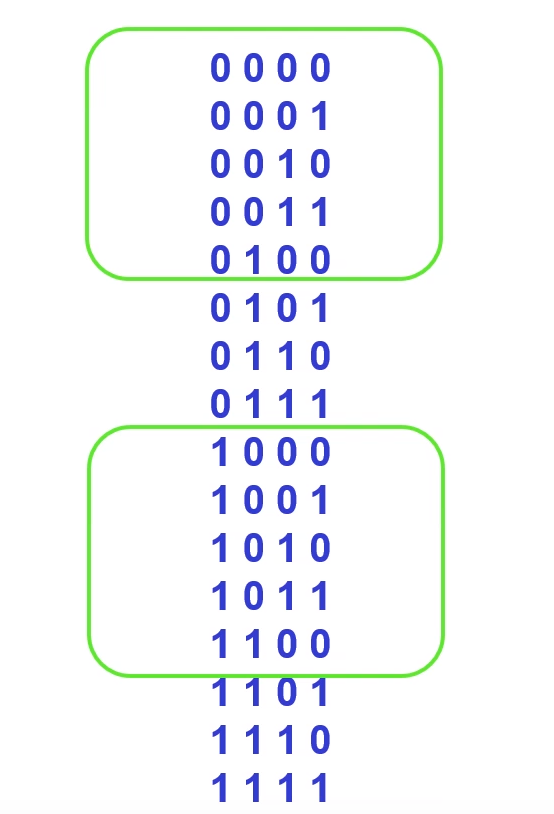
• 如何在二进制的16组合里面取出十个来表示0-9呢？实际上，我们可以从0000开始到1001结束作为选择，也可以在其他地方进行选取，只要这十个二进制编码互相不重复并且好记、好进行运算转换为10进制就可以了。

  选择1，这个是8421码：为什么叫8421，因为按照位权来计算，从左往右依次是8，4，2，1。8421码是最常用到的二进制转换十进制的编码。
  

选择2，这个是5421码：

按照位权来计算，从左往右依次是5，4，2，1。在选取二进制数的时候由于中间跳过了3位，所以它的最高位的位权由8变成了5，这个就是5421码的由来。

5421码的特点：高位互反，其他位上下两边对应。0000高位是0，其余低位是000，1000高位是1，其余低位是000，高位互反，其他位对应。

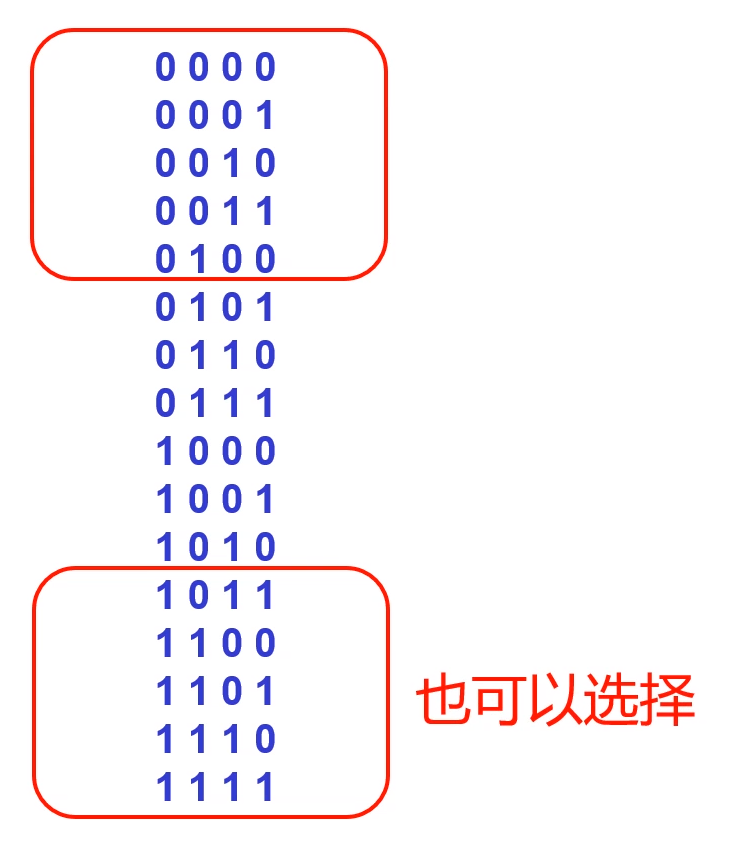
选择3，这个是2421码：

按照位权来计算，从左往右依次是2，4，2，1。在选取二进制数的时候由于中间跳过了6位，所以它的最高位的位权由8变成了2，这个就是2421码的由来。

2421码的特点：互反，第1个二进制数和最后1个二进制数是相反的。0000和1111互反，0001和1110互反...

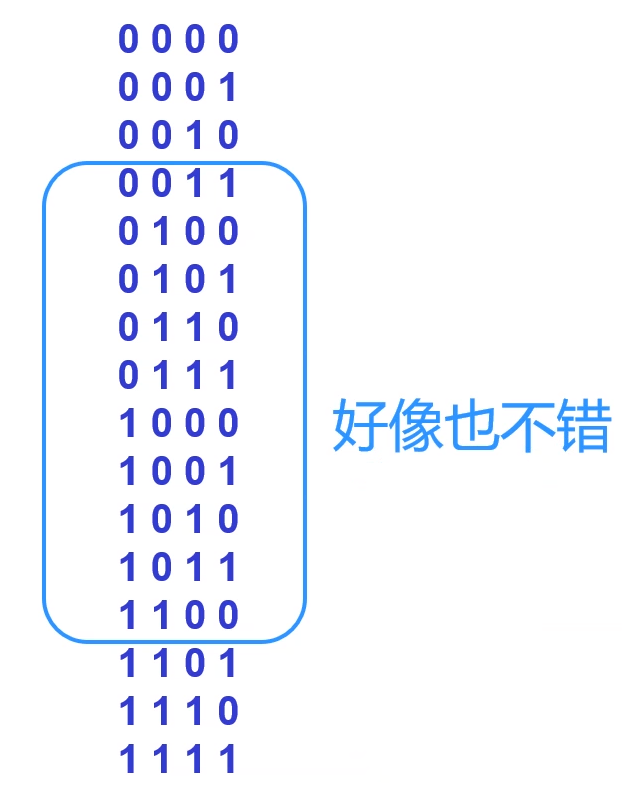
选择4，这个是余3码：

余3码在选取二进制数的时候，每一个二进制数都比顺序码（8421码）多出3（8421码+3），所以叫做余3码。

余3码也有上下互反的特点。

其中8421码、2421码、5211码都属于权位码，即每1位对应一个权值，如8421码中，各位的位权依次是8、4、2、1，将二进制1001转换为十进制数是这样的：8+0+0+1=9。

其他编码就是无权码，无权码每位的权并不确定。因此不能用按权展开的方法来求它所代表的十进制数。无权码在数字系统中不能进行数值运算。但是这些代码都有其特点，在不同的场合可以根据需要选用。

4、格雷码（余3循环码）

顺序二进制编码简单且容易切换，但在相邻的两个编码之间，可能同时有多个二进制位发生变化，例如代码0111变化为1000时，4个二进制位均发生了变化。在数字系统中，常常需要代码按一定顺序变化，但如果多个位同时发生变化，由于各个位变化在时间上的差异，往往会出现短暂的其他代码，例如代码0111变化为1000时，可能会出现短暂的1111或1011等，这有可能会导致严重的电路状态错误。使用格雷码可以避免这种错误的发生。

格雷码又称循环码，它的主要特点是相邻两个编码之间只有一个位不相同，在变化的时候，只会有一位数进行变化。列如：格雷码0000->0001->0011，可以发现只有一位数有变化。

1、格雷码具有以下3种特性：

• 反射特效：16个格雷码从中开始看，第7位格雷码和第8位的格雷码高1位是相反的，低3位数相同的。
  

• 逻辑相邻：格雷码任意两个相邻的数只有一个位不相同，0000->0001->0011，可以发现只有一位数有变化。

• 余3循环：将余3码转换成格雷码则称为余3循环码，第1个二进制数0010和最后一个二进制数1010也是只有1位不同，所以就循环回来了。
  

2、二进制码与格雷码转换

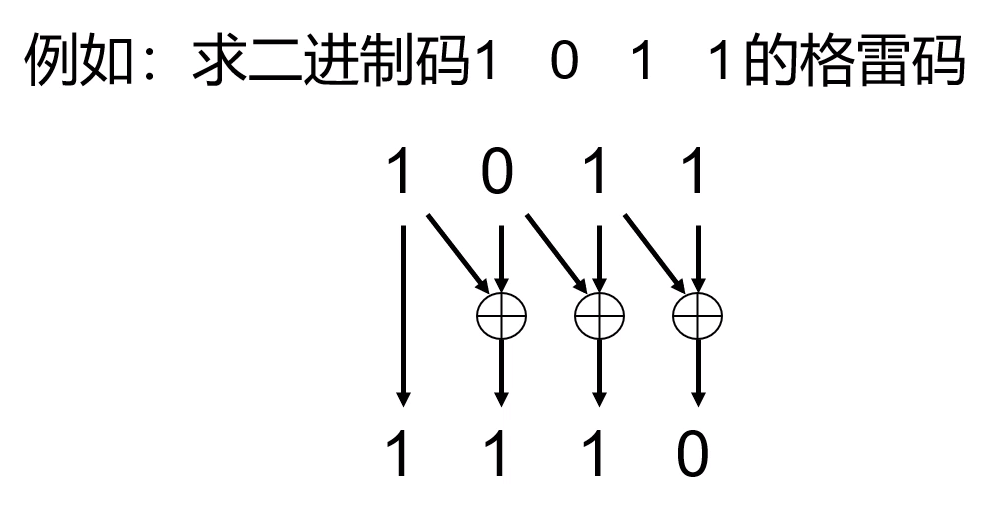
使用异或运算能够很方便的计算出格雷码，异或运算公式：0+0=0，0+1=1，1+1=0，由此可见只有加号两边不相等时结果才为1，相同为0。

在二进制码转换格雷码的时候，二进制码的最高位和格雷码的最高位是相同的，其他位置是通过相邻之间的数值异或运算计算出来的。

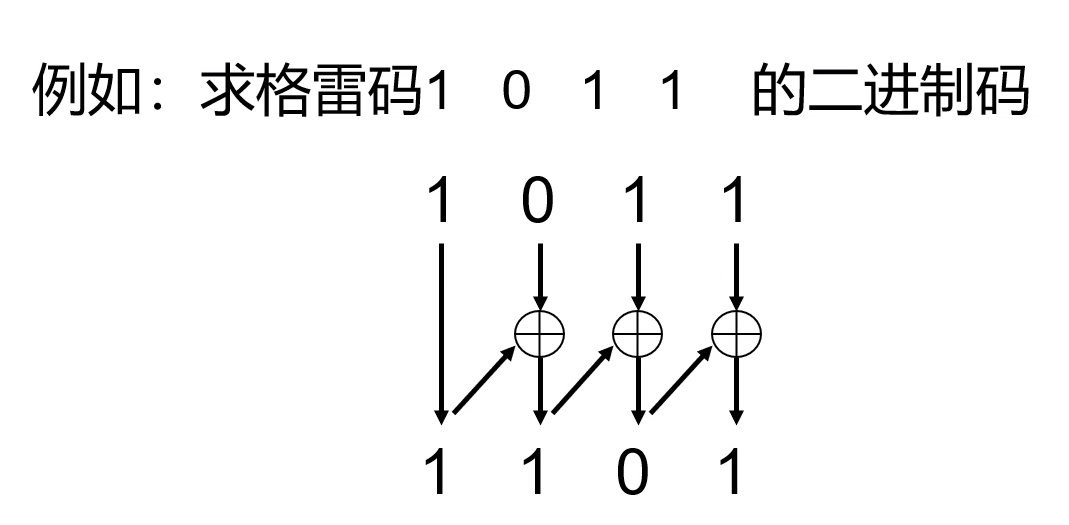
在格雷码转换二进制码的时候，二进制码的最高位和格雷码的最高位是相同的，其他位置是通过左边上次的异或运算结果和右边的数值异或运算计算出来的。

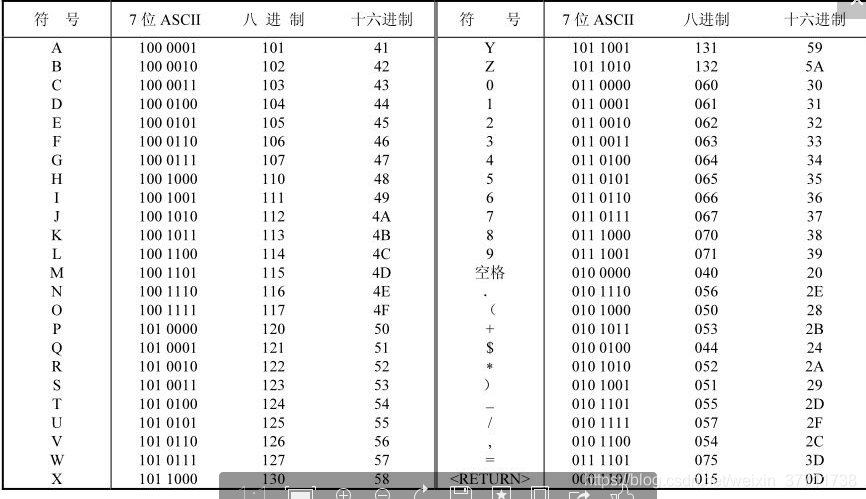
5、ASCII字符集码

除了数字数据外，计算机还必须能处理非数字信息。即计算机应能识别表示字母、标点符号和其他特殊符号以及数字的代码。这些代码叫做字符数字码。一个完整的字符数字码应包括26个小写英文字母、26个大写英文字母、10个数字符号、7个标点符号，以及其他20～40个特殊符号，如+、/、#、%、*等。也就是说，字符数字码能表示计算机键盘上所看到的各种符号和功能键。

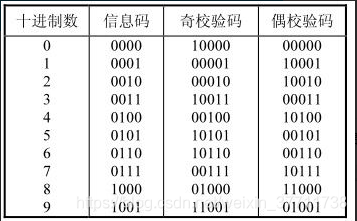
6、奇偶校验码（检错码和纠错码）

检错码:仅能检测数字信号是否发生错误。

纠错码:能够检测并纠正数字信号中的错误

奇偶校验码是一种具有检错能力的代码，它是在原代码（称为信息码）的基础上增加一个码位（称为校验码、校验位或附加位），使代码中含有的1的个数均为奇数（称为奇校验）或偶数（称为偶校验），这样通过检查代码中含有的1的数目的奇偶性来判别代码的合法性。显然，信号在传送过程中如果代码有两位出错，则这种奇偶校验法是无法检测的，因为两位出错不会改变代码中含1码个数的奇偶性。所以，奇偶校验码仅适用于信号出错率很低，且出现成对错误的概率基本为0的情况。