从Java看数据结构之——树和他的操作集

写在前面

树这种数据结构在计算机世界中有广泛的应用，比如操作系统中用到了红黑树，数据库用到了B+树，编译器中的语法树，内存管理用到了堆（本质上也是树），信息论中的哈夫曼编码等等等等。而树的实现和他的操作集也是笔试面试中常见的考核项目。

树的实现

与C语言的结构体+指针的实现方式不同，Java中树的实现当然是基于类。以二叉树为例，树的实现可以用下面这样的形式：

public class BinaryTree<T extends Comparable<T>> {
    private BinaryTree<T> root;
    //定义存储内容：内容、左子树、右子树
    public class Node<T extends Comparable<T>>{
        T data;
        BinaryTree<T> left;
        BinaryTree<T> right;
        //也可以有父节点
        BinaryTree<T> parent;

        public Node(T data, BinaryTree<T> left, BinaryTree<T> right, BinaryTree<T> parent) {
            this.data = data;
            this.left = left;
            this.right = right;
            this.parent = parent;
        }
    }
    
    //定义方法：增、删、查、改。

    public boolean insert(int x){
        ...
    }
    public boolean delete(int x){
        ...
    }
}

要注意，为了清晰树中数据的含义，我们一般不直接把树节点当做其成员变量，而是在其中新建内部类将其打包。针对子节点不止2个的多叉树，只需要把上面的left，right等合并成一个BinaryTree<T>类型的数组即可。

树的遍历

树的遍历应当是我们的基本功，里面涉及了后面图论算法中的深度优先搜索（DFS）和广度优先搜索（BFS），因此虽然简单但也很重要。在树的遍历中，往往对应着递归算法和非递归算法（层序遍历除外）。递归算法往往能写出很精简的代码，但是运行过程中会占用大量的系统资源。因此，非递归算法在这一点上还是更有优势。我们也应该更着重记忆他的非递归算法。面试过程中，我们甚至可以和面试官讨论所要求的写法。

先来看看前中后序遍历的递归写法：

public void preOrderTraversal(BinaryTree<T> tree){
    if(tree==null) return;
    System.out.print(tree.node.data+" ");
    preOrderTraversal(tree.node.left);
    preOrderTraversal(tree.node.right);
}

 

 

//中序遍历
public void inOrderTraversal(BinaryTree<T> tree){
    if(tree==null) return;
    inOrderTraversal(tree.node.left);
    System.out.print(tree.node.data+" ");
    inOrderTraversal(tree.node.right);
}

 

//后序遍历
public void pastOrderTraversal(BinaryTree<T> tree){
    if(tree==null) return;
    pastOrderTraversal(tree.node.left);
    pastOrderTraversal(tree.node.right);
    System.out.print(tree.node.data+" ");
}

 

看起来相当简单，也相当好记对吧。再来看非递归怎么在Java中实现：

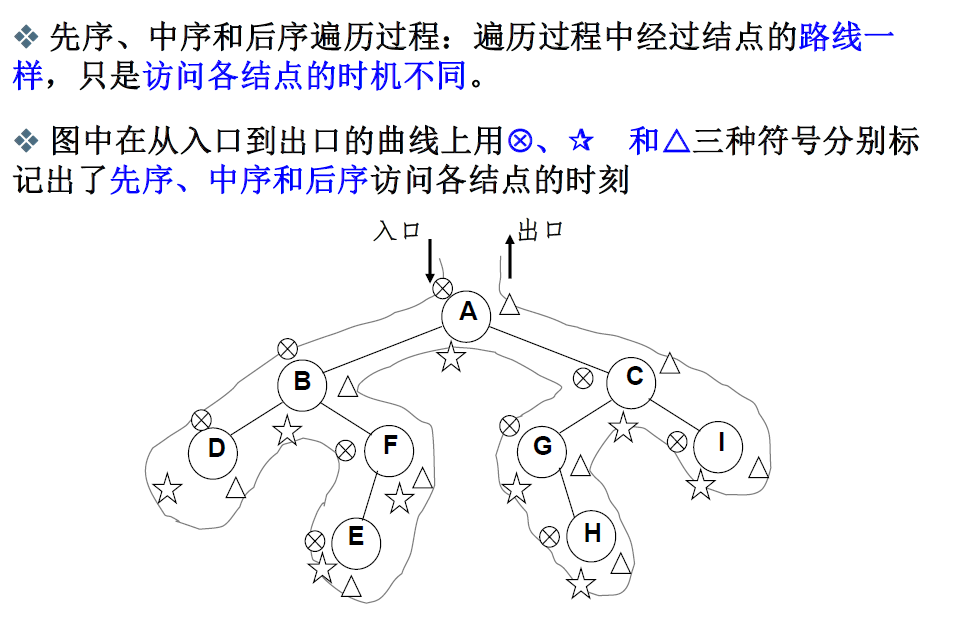
树的前序遍历和中序遍历的非递归算法都是用堆栈来实现，具体实现如下。

public void preOrderTraversal(){
    Stack<BinaryTree<T>> st = new Stack<>();
    BinaryTree<T> tmp = this;
    while(tmp!=null || !st.empty()){
        while(tmp!=null){
            System.out.print(tmp.node.data+" ");
            st.push(tmp);
            tmp=tmp.node.left;//一路向左
        }
        if(!st.empty()){
            tmp=st.pop();
            tmp=tmp.node.right;//偶尔向右
        }
    }
    System.out.println();
}

 

public void inOrderTraversal(){
    Stack<BinaryTree<T>> st = new Stack<>();
    BinaryTree<T> tmp = this;
    while(tmp!=null || !st.empty()){
        while(tmp!=null){
            st.push(tmp);
            tmp=tmp.node.left;
        }
        if(!st.empty()){
            tmp=st.pop();
            //输出变到这里，仅此而已
            System.out.println(tmp.node.data);
            tmp=tmp.node.right;
        }
    }
}

后序遍历思路相似，由于后序遍历是第三次经过才进行输出（见上图），而上面的while循环和if代码块分别表示第一次见和第二次见，因此需要增加一个标志位在每一个节点，用来标明是不是在if代码块中第一次看见它。这么说并不明显，自己实现一遍应该会印象深刻一点。

//后续非递归
public void PastOrderTraversal(){
    BinaryTree<T> Tmp = this;
    Stack<BinaryTree<T>> st = new Stack<>();
    while(Tmp!=null || !st.empty()){
        while(Tmp!=null){
            st.push(Tmp);
            Tmp=Tmp.node.left;
        }
        if(!st.empty()){//if代码块
            Tmp=st.pop();
            if(Tmp.node.IsFirstTraversal){//这里判断是不是第一次进if代码块
                Tmp.node.IsFirstTraversal=false;//进来过了，置位false，下一次就可以输出了
                st.push(Tmp);
                Tmp=Tmp.node.right;
            }
            else{//不是第一次，输出
                System.out.print(Tmp.node.data+" ");
            }
        }
    }
}

 

层序遍历只有非递归写法，没有递归的方法。层序遍历利用的数据结构是队列。遍历应该先从根节点开始，首先将根节点入队，然后开始执行循环：节点出队、访问节点（print）、左右儿子入队。

 

//层序遍历
public void levelOrderTraversal(){
    Queue<BinaryTree<T>> tQueue = new ArrayDeque<>();
    BinaryTree<T> tmp = this;
    tQueue.add(tmp);
    while(!tQueue.isEmpty()){
        tmp = tQueue.remove();
        System.out.print(tmp.node.data+" ");
        if(tmp.node.left!=null) tQueue.add(tmp.node.left);
        if(tmp.node.right!=null) tQueue.add(tmp.node.right);
    }
}

操作集

1.插入

    private BinaryTree<T> insert(BinaryTree<T> t, Node<T> n){
        if(t==null) {
            t = new BinaryTree<>();
            t.node = n;
            return t;
        }
        int cmp = n.data.compareTo(t.node.data);
        if(cmp==0) return null;//节点存在
        else if(cmp<0) t.node.left = insert(t.node.left, n);
        else t.node.right = insert(t.node.right, n);
        return t;
    }

    public void insert(T x){
        Node<T> n = new Node<>(x,null, null, null);
        if(this.node==null){
            this.node = n;
            return;
        }
        insert(this,n);
    }

2.查找

普通查找比较好实现，这个就是利用了二分查找的思想。

　　 /**
     * 查找
     * @param t 树
     * @param x 查找的值
     * @return 值所在树
     */
    private BinaryTree<T> find(BinaryTree<T> t, T x){
        int cmp = x.compareTo(t.node.data);
        if(cmp==0){//找到了
            return t;
        }
        else if(cmp<0) return find(t.node.left,x);
        else return find(t.node.right,x);
    }

    public BinaryTree<T> find(T x){
        return find(this, x);
    }