引入:
在竞赛中我们经常会遇到很多很多你望而却步的题,,不是你的基础知识不扎实,而是这些题都考的是你的思维能力,而不是你学了多少的算法,,,,
下面我们有一道题开始:--//图片来自:
https://blog.csdn.net/chichoxian/article/details/20871497
这道题十分经典,相信oier们都做过.
我就在此给同我一样菜的oier讲讲这道题的思路吧。
然后我发现了一个事实,好像我贴的是英文题目!!!
重来一遍:
描述:
一群蚂蚁在长度为1厘米的水平杆上行走,每根杆的速度恒定为1厘米/秒。当一只行走的蚂蚁到达极的一端时,它会立即脱落。当两只蚂蚁相遇时,它们会转身向相反方向开始行走。我们知道蚂蚁在杆子上的原始位置,不幸的是,我们不知道蚂蚁行走的方向。你的任务是计算所有蚂蚁从杆上掉下来所需的最早和最晚时间。
输入:
第一行输入包含一个整数,给出后面的案例数。每种情况的数据都以两个整数开始:极点的长度(cm)和n,极点上的蚂蚁数量。这两个数字后面跟着n个整数,它们将每个蚂蚁在杆上的位置作为从杆的左端测量的距离,没有特别的顺序。所有输入整数都不大于1000000,它们由空格分隔。
输出:
对于每种输入情况,输出由单个空格分隔的两个数字。第一个数字是所有蚂蚁从杆上掉下来的最早时间(如果他们的步行路线选择得恰当),第二个数字是最新可能的时间。
题意概括:一些蚂蚁以1cm/s的速度在长度为Lcm的水平杆上爬行,爬到端点就会掉下去。当两只蚂蚁相遇,它们就会立刻掉头返回。已知L和一开始每只蚂蚁的位置,但不知道它们的方向,求它们最早何时全部掉落,最迟何时全部掉落。
最多1,000,000只蚂蚁
分析:
这里大家首先想到的是模拟吧(哈哈,和我一样),但是模拟用循环嵌套的话对于每只蚂蚁,都有两种情况,那么一共就是2^n的时间复杂度,看一下题设要求,(好吧这里忘写了n最大是10^6),如果用循环模拟这种n^3的方法的话,必定RE,所以我们要想出一种在一秒内就可以解决的方法,1秒的时间复杂度对于此题来讲是只能为O(n)或则O(1)的,所以我们要找出这个O(n)的方法(这个已经够了),,,,,
怎么做呢?我反正是不会的,老师讲后我才明白,,,
我们先看题:这里是说每只蚂蚁互相碰到后就会掉头,然后每只蚂蚁间持续这样,直到它们都掉下去,我们想一想,两只蚂蚁碰头后又返回,不就像互相继承了对方的方向吗???
看图:更好理解
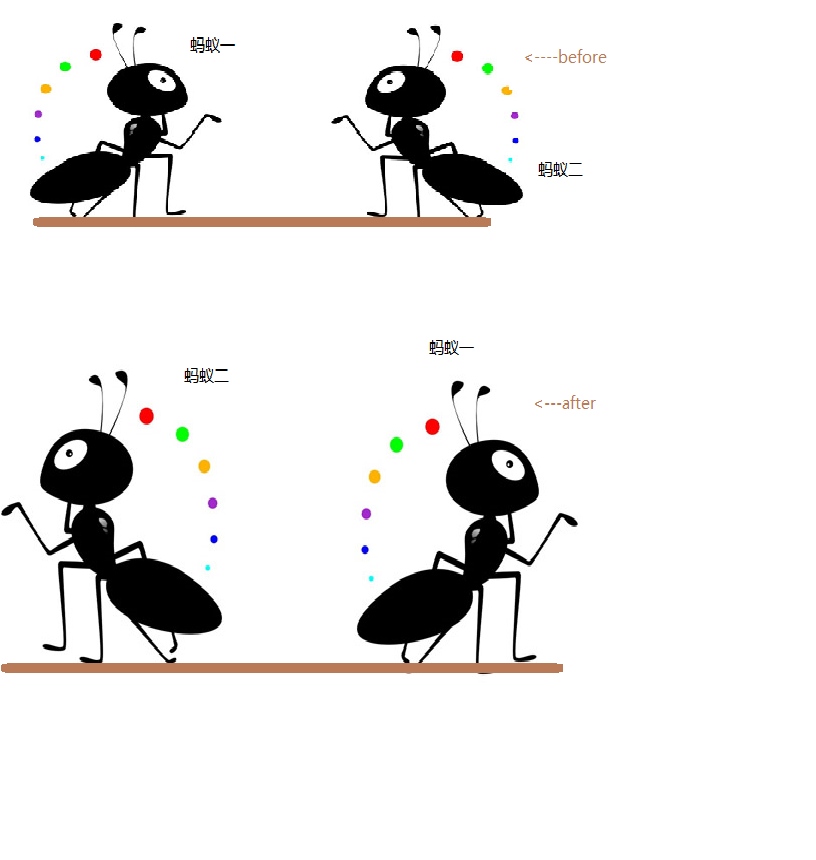
我们可以这样形象的理解:蚂蚁一和蚂蚁二身体是中空的,它们互相穿过了对方,只不过交换了对方的名号而已,,,
其实,说了这么多,我只是想让你想明白一点:
蚂蚁都是一样的,所以当两只蚂蚁相遇时转向跟没转向也是一样的,因为每只蚂蚁都会继承另一只蚂蚁的方向,所以可以视为蚂蚁方向没有变过,所以最短时间就是所有蚂蚁距端点最近距离的最大值,最长时间就是所有蚂蚁距端点最远距离的最大值。
好了贴代码吧:(此处只放核心代码)

这道题你懂了吗???
那我们现在再来拓展一下;

这道题看名字肯定与第一题相关,但是做起来可不一样,我们发现最难的就是定下蚂蚁的状态,并且输出它的位置。
解题思路:
定义一个数据结构 “”蚂蚁” ---用struct可以记载当前位置,编号(第几只蚂蚁),和左右方向
并且我们规定左为-1,右为1,转向为0
还要用三个数组分别记载:1.原蚂蚁序列 2.后来的蚂蚁序列 3.各个蚂蚁的编号--(其实就是它的位置,原因在下面!!)
我们在图上模拟可得,蚂蚁之间互相碰到便掉头,则他们之间巧妙的维护了一种相对平衡的位置顺序,,你模拟看看就知道了,,,
然后我们其实并不能一个一个的算蚂蚁相撞的位置在哪,然后判定他们的方向,因为,时间复杂度太大,工作量也太大,我们直接现将原蚂蚁序列的顺序记录下来,并将其排序,,先不管他们会不会掉下去,直接把他们的位置累加出来,,最后来判断(其中的一个操作便是排序),最后排序输出就行了!
贴代码:
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define maxn 10005 using namespace std; struct Ant { int id; // int p; int d; bool operator < (const Ant &other) const { return p < other.p; } }before[maxn],after[maxn]; const char dirName[][10] = {"L","Turning","R"}; int order[maxn]; int main() { int L,T,n; scanf("%d%d%d",&L,&T,&n);//输出 for(int i = 0;i < n;i++) { int p,d; char c; scanf("%d %c",&p,&c); d = (c == 'L' ? -1 : 1); before[i] = (Ant){i,p,d};//初始化 after[i] = (Ant){0,p+T*d,d}; } sort(before,before+n);//排序 for(int i = 0;i < n;i++) order[before[i].id] = i;//记录下相对位置---编号 sort(after,after+n);//排序 for(int i = 0;i < n - 1;i++) if(after[i].p == after[i+1].p) after[i].d = after[i+1].d = 0;//判断是否相撞--即处于一点 for(int i = 0;i < n;i++) { int a = order[i]; if(after[a].p < 0 || after[a].p > L)//输出 printf("Fell off\n"); else printf("%d %s\n",after[a].p,dirName[after[a].d+1]); } return 0; }
好了,,就到这吧!!!qwq



