呃,,,,上次我们讲到了如何进行区间查询,(其实并不详细),因为---查询一个特定的区间时可以进行一系列的操作:1,查询最值 2,查询区间和 ---等等都要根据题意修改,,这就是为什么线段树的题目十分灵活的原因了。
再此补充一下,建树的时候,数组要开到题设的四倍,以防溢出!!!
单点修改于区间修改(更新)
单点修改与区间修改完全不同,此处放个图理解一下:
图来自大佬博客:https://www.cnblogs.com/ACworker/p/7703537.html(具体模拟过程可见此博客)

此处的单点是某个集合中的元素的值而区间修改则是对节点(区间)的值进行修改
然后,,,,,显而易见,单点修改只用改变这个点所处的单链的值,而区间修改则不同
如图修改
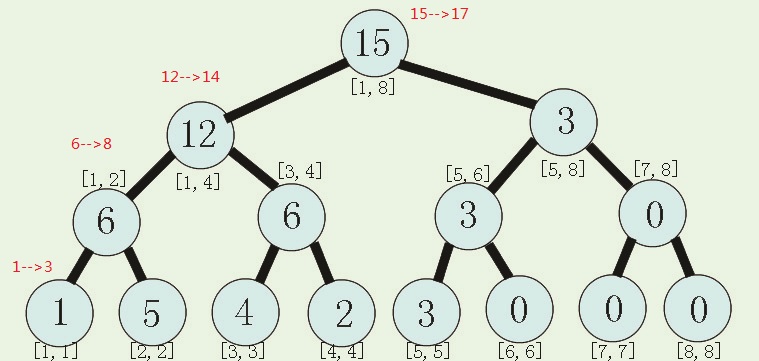
代码附上:
void change(int k,int l,int r,int x,int v) //x为原序列的位置,v为要改变的值 { if(r<=x||l>x) return ;//若当前区间与原序列位置无交集 if(l==r&&l==x) { tr[k]==v;//修改叶节点 return ; } int mid=(l+r)/2; change(k*2+1,mid+1,r,x,v);//修改左区间 change(k*2,l,mid,x,v);//修改右区间 tr[k]= min(tr[k*2+1],tr[k*2]); }
然后区间修改---此处有两个方法:1.出现一个要修改的区间就要查询上下区间直接修改--此处要用到lazy标记,待会再讲 2.现将要修改的值放在此节点(访问区间)上,查询时累加就行---这个叫做标记永久化的东西
1.lazy标记法
区间修改,就是修改一整段的值。第一种方法是进行循环单点修改,但是这样复杂度显然太大……为了能节省复杂度,我们有一种方法,就是使用lazy标记,我们修改一个区间的时候,并不需要把区间中的所有值即刻修改,只要在访问的时候修改即可。那么我们对于修改的区间打上lazy标记,记录要修改的值即可。如果是求和的话一定要在下放lazy标记的时候乘以区间长度。
void down(int k) { tr[k*2].lazy+=tr[k].lazy; tr[k*2+1].lazy+=tr[k].lazy; tr[k*2].w+=(tr[k*2].r-tr[k*2].l+1)*tr[k].lazy; tr[k*2+1].w+=(tr[k*2+1].r-tr[k*2+1].l+1)*tr[k].lazy; tr[k].lazy=0; } //记住要把lazy标记向后传
2.标记永久化
其实就是维护一个标记,然后不动,查询时再累加就行了。
此处就不详讲,推荐一个博客:https://www.cnblogs.com/cjoieryl/p/8213354.html(专门讲标记永久化的)
///////////////////////////////////////////////基本操作就是这些,下面就是模板题了。
/////////但在此之前再加两点线段树的性质:1’对于当前的节点k,其左孩子的下标为k*2,右孩子的下标k*2+1 2’左孩子管辖的区间范围为(l,mid);右孩子管辖的区间范围为(mid+1,r);
/////////////////////////////////////////////////////////////贴题////////////////////////////////////////////////////////////////////

这道题是模板题,,,,,,
代码附上:
#include <iostream> #include <cstdio> using namespace std; struct tree { int l,r; long long w; int lazy; }tr[500000]; long long ans; void build(int l,int r,int k) { tr[k].l=l; tr[k].r=r; if(l==r) { scanf("%d",&tr[k].w); return; } int mid=(l+r)/2; build(l,mid,k*2); build(mid+1,r,k*2+1); tr[k].w=tr[k*2].w+tr[k*2+1].w; } void down(int k) { tr[k*2].lazy+=tr[k].lazy; tr[k*2+1].lazy+=tr[k].lazy; tr[k*2].w+=(tr[k*2].r-tr[k*2].l+1)*tr[k].lazy; tr[k*2+1].w+=(tr[k*2+1].r-tr[k*2+1].l+1)*tr[k].lazy; tr[k].lazy=0; } void add(int l,int r,int num,int k) { if(tr[k].l>=l&&tr[k].r<=r) { tr[k].lazy+=num; tr[k].w+=(tr[k].r-tr[k].l+1)*num; return; } if(tr[k].lazy) down(k); int mid=(tr[k].l+tr[k].r)/2; if(l<=mid) add(l,r,num,k*2); if(r>mid) add(l,r,num,k*2+1); tr[k].w=tr[k*2].w+tr[k*2+1].w; } void ask(int l,int r,int k) { if(tr[k].l>=l&&tr[k].r<=r) { ans+=tr[k].w; return; } if(tr[k].lazy) down(k); int mid=(tr[k].l+tr[k].r)/2; if(l<=mid) ask(l,r,k*2); if(r>mid) ask(l,r,k*2+1); //tr[k].w=tr[k*2].w+tr[k*2+1].w; } int main() { freopen("truffle.in","r",stdin); freopen("truffle.out","w",stdout); int n,m,x; cin>>n>>m>>x; build(1,n,1); int type,a,b,c; for(int i=1;i<=m;i++) { scanf("%d%d%d",&type,&a,&b); if(type==1) { ans=0; ask(a,b,1); if(ans<=x) cout<<"yes\n"; else cout<<"no\n"; } else { scanf("%d",&c); add(a,b,c,1); } } fclose(stdin); fclose(stdout); return 0; }
然后你会发现,此题十分简单,,但是下一题:

这道题就是一个变形,但是他需要你十分灵活的变形,以及对模板题的深刻理解:(我也很懵)
题解:
#include<iostream> #include<cstdio> #include<cstdlib> #include<algorithm> using namespace std; const int MAXN=5e5+10; struct Tree { int l,r; int ls,rs,maxs; int sum; }tr[MAXN*4]; int n,m; int scor[MAXN]; void push_up(int root) { tr[root].sum=tr[root<<1].sum+tr[root<<1|1].sum; tr[root].ls=max(tr[root<<1].ls,tr[root<<1].sum+tr[root<<1|1].ls); tr[root].rs=max(tr[root<<1|1].rs,tr[root<<1|1].sum+tr[root<<1].rs); tr[root].maxs=max(max(tr[root<<1].maxs,tr[root<<1|1].maxs),tr[root<<1].rs+tr[root<<1|1].ls); } void build(int root,int l,int r) { tr[root].l=l; tr[root].r=r; if(l==r) { tr[root].ls=tr[root].rs=tr[root].maxs=tr[root].sum=scor[l]; return ; } int mid=l+r>>1; build(root<<1,l,mid); build(root<<1|1,mid+1,r); push_up(root); } void update(int root,int l,int r,int x,int key) { if(l==r) { tr[root].ls=tr[root].rs=tr[root].maxs=tr[root].sum=key; return ; } int mid=l+r>>1; if(x<=mid) update(root<<1,l,mid,x,key); else update(root<<1|1,mid+1,r,x,key); push_up(root); } Tree query(int root,int L,int R) { if(L<=tr[root].l&&tr[root].r<=R) return tr[root]; int mid=tr[root].l+tr[root].r>>1; if(R<=mid) return query(root<<1,L,R); if(L>mid) return query(root<<1|1,L,R); Tree ans,ans1=query(root<<1,L,mid),ans2=query(root<<1|1,mid+1,R); ans.l=ans1.l,ans.r=ans2.r; ans.ls=max(ans1.ls,ans1.sum+ans2.ls); ans.rs=max(ans2.rs,ans2.sum+ans1.rs); ans.maxs=max(max(ans1.maxs,ans2.maxs),ans1.rs+ans2.ls); ans.sum=ans1.sum+ans2.sum; return ans; } int Read() { int i=0,f=1; char c; for(c=getchar();(c>'9'||c<'0')&&c!='-';c=getchar()); if(c=='-') f=-1,c=getchar(); for(;c>='0'&&c<='9';c=getchar()) i=(i<<3)+(i<<1)+c-'0'; return i*f; } int main() { freopen("drive.in","r",stdin); freopen("drive.out","w",stdout); cin>>n>>m; for(int i=1;i<=n;++i) scor[i]=Read(); build(1,1,n); while(m--) { int cz=Read(),l=Read(),r=Read(); if(cz==1) { if(l>r) swap(l,r); printf("%d\n",query(1,l,r).maxs); } else update(1,1,n,l,r); } return 0; }
好了到了这里,,如果你还是神清气闲,那你一定可以ak所有线段树的题啦!(我反正不行)
推荐题目
洛谷p4513
:
题意。。。很明显看出要维护区间子序列最大值,那么问题就在于如何在区间合并的时候更新区间子序列最大值。
可以推出,区间子序列最大值要么是从最左边开始的一段,要么是最右边向左的一段,
要么是中间的一段,对于第一种,我们发现要么是左儿子最左边的一段,
要么是左儿子+右儿子左边一段,第二种同理。
对于第三种,要么是左儿子的最大值,要么是右儿子的最大值,
要么是左儿子的右边的一段与右儿子的左边的一段拼起来。
题解:
呃,,去洛谷上看吧,,,,over。



