线段树基础知识----（基础数据结构）--（一）

 1.定义

引入：为什么要使用线段树而不用数组模拟呢？

answer:因为有些题用数组来做就要超时，用线段树的O(log(n))的时间复杂度刚好可以求解

毫无疑问线段树是一种数据结构，但是它实际是一个类似树状的链表结构（个人认为）

///还是要正经一点（照搬教科书）----------- /

//////////////////////////////////////////////////////////////////////

线段树定义：线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。

2.线段树的基础操作

 线段树的基本操作分为：{1.建立树形结构 2.对某个特定区间进行查询 3.修改某个点的值 4.修改某个区间的值 5.查询某个区间的最大最小值 6.查询区间的区间和}

那我就一个一个的说吧........

3.实际一点

先说前提--一定要建立一个树状的数据结构--如下

#include <iostream>
#include <cstdio>
#define maxn 500000
using namespace std;

struct tree
{
    int l,r;
    long long w;
    int lazy;
}tr[maxn*4];

//l,r代表左右子树,w代表区间的值(每个节点的值),lazy自有用处---详细见后

对于线段树中的每一个非叶子节点[a,b]，它的左儿子表示的区间为[a,(a+b)/2]，右儿子表示的区间为[(a+b)/2+1,b]。因此线段树是平衡二叉树，最后的子节点数目为N，即整个线段区间的长度。
主要遇到的问题：
要解决计算某一数组任意区间长度，并且在随机改变一个值后，在计算这个区间和
运用线段树可以降低时间复杂度。--从O(n)降低到O(logn)
主要涉及三个函数
1.根据所给数组，创建一个线段树（满二叉树，不够补0）
2.改变一个值，更新线段树
3.计算L-R的区间和
4.具体操作及代码（算法思想）

建树：我们知道线段树是一种二叉搜索树，它的建立就一定要运用到二分思想，每个节点都只有左子树和右子树，所以此处也要用到递归思想，具体建立如下

void build(int l,int r,int k)
{
    tr[k].l=l;
    tr[k].r=r;
    if(l==r)
    {
        scanf("%d",&tr[k].w);
        return;
    }
    int mid=(l+r)/2;
    build(l,mid,k*2);
    build(mid+1,r,k*2+1);
    tr[k].w=tr[k*2].w+tr[k*2+1].w;
}

此处mid的使用就体现了二分思想

再次我给一个例子：将1--10建成一个线段树--如图（更好理解）

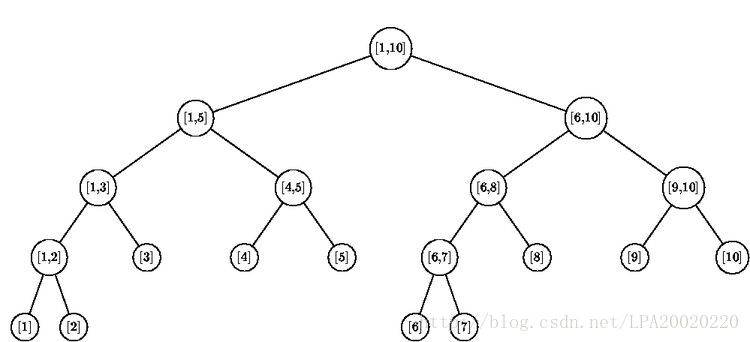
记住--线段树只是一个数据结构，它的每一个节点都是一个区间(相当于集合)

 查询区间

引自  岩之痕 大佬 >https://blog.csdn.net/zearot/article/details/52280189

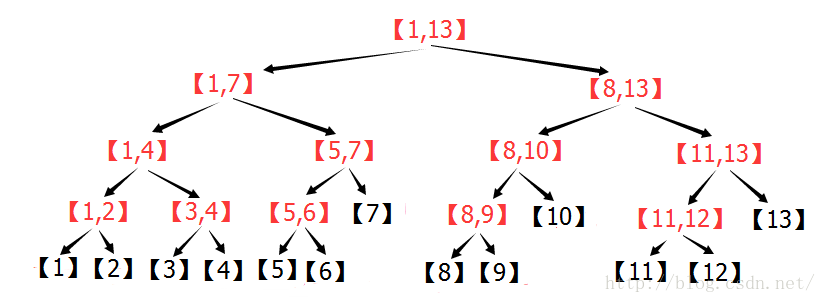
查询区间的思想是将要询问的区间与现在处在的区间进行比较，我们模拟一下很容易知道，要查询的区间只有两种情况：我们那上图来做例子---1.查询2---4（包括在某个已经分好的节点（区间）中的--说白了就是被左或右区间包括的集合）---2.查询6---10（此区间与左和右区间有交集）--集合学得好的童鞋应该很容易理解

具体代码实现如下

void ask(int l,int r,int k)
{
    if(tr[k].l>=l&&tr[k].r<=r)
    {
        ans+=tr[k].w;
        return;
    }
    if(tr[k].lazy)
        down(k);
    int mid=(tr[k].l+tr[k].r)/2;
    if(l<=mid)
        ask(l,r,k*2);
    if(r>mid)
        ask(l,r,k*2+1);
    //tr[k].w=tr[k*2].w+tr[k*2+1].w;
}

好了，，查询和建树就先讲到这里，，下面的请看线段树基础知识--(基础数据结构)--二