B - Bicoloring (二分图判定)C - Catch

 

 

B - Bicoloring

参考2：Bicoloring (并查集/二分图)

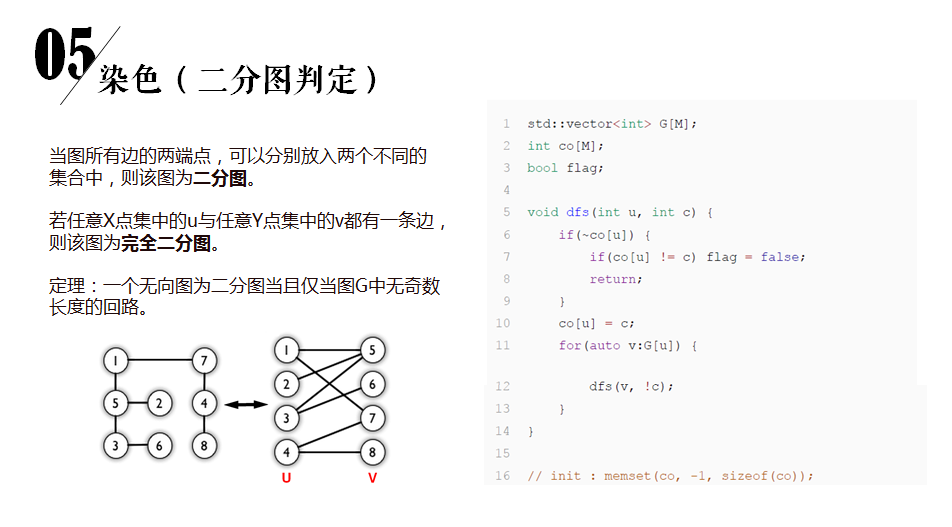
题意：判断此图是否为二分图（染色法，相邻两点不同色）

AC代码：

 1 /***********************************************/
 2 
 3 int co[250];
 4 
 5 struct node{
 6     int v;
 7     node(){}
 8     node(int _v):v(_v){}
 9 };
10 vector<node>G[250];//邻接表法 
11 
12 int fff=0;
13 
14 void dfs(int now,int pre)
15 {
16     if(~co[now])
17     {
18         if(co[pre]!=0) co[now]=-co[pre];
19         else co[now]=1;//头结点染色
20         //cout<<"co"<<G[now].size()<<endl;
21         for(int i=0;i<G[now].size();i++)
22         {
23             if(fff==0 && G[now][i].v!=pre)
24             dfs(G[now][i].v,now);
25         }
26     }
27         
28     else{//染过 
29         if(co[now]==co[pre]){
30             fff=1;
31         }
32     } 
33     
34 }
35 
36 int main()
37 {
38     int n,m;
39     while(cin>>n && n)
40     {
41         fff=0;
42         mem0(G);
43         cin>>m;
44         for(int i=1;i<=m;i++){
45             int a,b;
46             cin>>a>>b;
47             G[a].push_back(node(b));
48             G[b].push_back(node(a)); 
49         }
50         mem0(co);
51         dfs(0,0);
52         //for(int i=0;i<n;i++) cout<<co[i]<<"tt";
53         if(fff){
54             cout<<"NOT BICOLORABLE."<<endl;
55         }
56         else cout<<"BICOLORABLE."<<endl;
57     }
58     return 0;
59 }
60 
61 /*
62 3
63 3
64 0 1
65 1 2
66 2 0
67 3
68 2
69 0 1
70 1 2
71 9
72 8
73 0 1
74 0 2
75 0 3
76 0 4
77 0 5
78 0 6
79 0 7
80 0 8
81 0
82 
83 */
View Code

 

C - Catch

 参考博客：【二部图的判定】Catch

 

题目大意:
　　有一个人，从S点出发，他可能朝任意一条路走到另外一点，走每一条路都需要花费1单位的时间，每一条路可以重复走，问，他是否能够在奇数时刻以及偶数时刻出现在同一点，而且，每个点都能够满足这一条件的话，则输出YES,否则输出NO。
解法：
　　在做这道题目之前，需要了解一下二部图的一些性质，如果一幅图为二部图的充分必要条件是，这幅联通图的任意一个环都为偶数环。
　　相对于，题目所要求的，要使得他能够在偶数时刻以及奇数时刻出现在同一点上，需要的是这个环必须是奇数环，因为奇数环的话，才能使得，在偶数或者奇数时刻出现在环上任意的同一点上，而且，只要联通图存在一个奇数环的话，也就能保存图上的任意一点都能过在偶数时刻以及奇数时刻出现。因为我们刚开始出发的时间为0，既为偶数时刻，连接它的下一点就是奇数时刻，你是从S点出发的，如果形成奇数环的话，也就是说明S点也能在奇数时刻到达，他的下一点也就能够变成偶数时刻了的，也就是说S可以变成偶数时刻出发以及奇数时刻出发，对于联通图上任意一点同样能够变成奇数时刻以及偶数时刻了的、如果他，不存在这一种情况的话，则说明这幅联通图上的环都为偶数环，也就是说这幅图是二部图，总而言之，其实就是让我们判断这幅图是不是二部图而已，是的话输出NO，不是的话输出YES即可。
AC代码：（scanf读入否则TLE）
 1 /***********************************************/
 2 
 3 int co[maxn];
 4 
 5 struct node{
 6     int v;
 7     node(){}
 8     node(int _v):v(_v){}
 9 };
10 vector<node>G[maxn];//邻接表法 
11 
12 int fff=0;
13 
14 void dfs(int now,int pre)
15 {
16     if(~co[now]){
17         if(co[pre]!=0) co[now]=-co[pre];
18         else co[now]=1;
19         
20         for(int i=0;i<G[now].size();i++)
21         {
22             if(fff==0 && G[now][i].v!=pre) dfs(G[now][i].v,now);
23         }
24     }
25     else
26     {
27         if(co[now]==co[pre]){
28             fff=1;//表示无法染色，不是二分图 
29             return ;
30         }
31     }
32 }
33 
34 int main()
35 {
36     int t;
37     cin>>t;
38     int ans=0;
39     while(t--)
40     {
41         int n,m,k;
42         sc3(n,m,k);
43         fff=0;
44         mem0(G);
45         //cout<<m;
46         for(int i=1;i<=m;i++){
47             int a,b;
48             sc2(a,b);
49             G[a].push_back(node(b));
50             G[b].push_back(node(a)); 
51         }
52         mem0(co);
53         dfs(0,0);
54         //for(int i=0;i<n;i++) cout<<co[i]<<"tt";
55         cout<<"Case "<<(++ans)<<": ";
56         if(fff){
57             printf("YES\n");
58         }
59         else printf("NO\n");
60     }
61     return 0;
62 }
View Code

 

posted @ 2019-01-25 14:17  liuyongliu  阅读(332)  评论(0)  编辑  收藏  举报