计算三角形面积

参考：已知三点坐标,求三角形面积

1: 已知直角坐标系3点p(a,b),m(c,d),n(e,f)求三角形pmn面积

两倍三角形面积是整型
代码模板：

ll solve(ll a,ll b,ll c,ll d,ll e,ll f)//计算两倍三角形面积
{
    return abs(a*d+b*e+c*f-a*f-b*c-d*e);
}

此写法可以不爆long long，之后再除以2即可

2: 若是由三条边求面积,则海伦公式

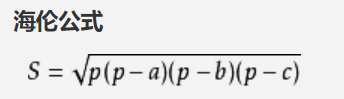
模板为：

double hailun(double a,double b,double c)
{//保证尽量不爆long long
    double s;
    double pp=(a+b+c)/2.0;
    double s1=sqrt(fabs(pp));
    double s2=sqrt(fabs(pp-a));
    double s3=sqrt(fabs(pp-b));
    double s4=sqrt(fabs(pp-c));
    s=s1*s2*s3*s4;
    return s;
}

3: 判断三点一线

bool judge(node a,node b,node c)
{
    return (c.x-a.x)*(b.y-a.y)-(c.y-a.y)*(b.x-a.x)!=0;
}

---

参考例题：https://ac.nowcoder.com/acm/contest/327/A

处女座的签到题
时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述

平面上有n个点，问：平面上所有三角形面积第k大的三角形的面积是多少?

输入描述

第一行T，表示样例的个数。
对于每一组样例，第一行两个整数n和k，
接下来n行，每行两个整数x,y表示点的坐标
T<=80
3<=n<=100
-109<=x,y<=109
对于每一组样例，保证任意两点不重合，且能构成的三角形的个数不小于k

输出描述

对于每一组样例，输出第k大三角形的面积，精确到小数点后两位（四舍五入）。

示例

输入

1
4 3
1 1
0 0
0 1
0 -1

输出

0.50

说明

样例中一共能构成3个三角形，面积分别为0.5，0.5，和1，面积第3大的为0.5
WA点：1,此题用海伦公式会爆double 和 long long
　　　 2,寻找第K大，若不用STL（nth_element），直接sort大法，会超时....

AC代码

#include <bits/stdc++.h>

using namespace std;
#define sc(a) scanf("%d",&a)
#define sc2(a,b) scanf("%d%d",&a,&b)
#define sc3(a,b,c) scanf("%d%d%d",&a,&b,&c)
#define scl(a) scanf("%lld",&a)
#define scl2(a,b) scanf("%lld%lld",&a,&b)
#define scl3(a,b,c) scanf("%lld%lld%lld",&a,&b,&c)
#define l_b lower_bound
#define u_b upper_bound

#define min_2(a,b) a<b?a:b
#define min_3(a,b,c) min_2(min_2(a,b),c)
#define max_2(a,b) a>b?a:b
#define max_3(a,b,c) max_2(max_2(a,b),c)
#define ll long long
#define rint register int
#define mem0(x) memset(x, 0, sizeof(x))
#define mem1(x) memset(x, -1, sizeof(x))
#define lowbit(x)  x&-x
/**inline int read()///神奇的读优
{
    int x=0,f=1;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
    return x*f;
}*/
///2147483647 -2147483648
///9223372036854775807 -9223372036854775808
//freopen("input.txt", "r", stdin);
const double PI=acos(-1.0);
const int inf = 0x3f3f3f3f;
const ll inff = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9+7;
const int maxn= 1e8+5;

//map<ll,ll>mp;
//set<ll>st;
//stack<>st;
//queue<>Q;
/***********************************************/
vector<ll>V;
ll x[200+3],y[200+3];


ll solve(ll a,ll b,ll c,ll d,ll e,ll f)
{
    return abs(a*d+b*e+c*f-a*f-b*c-d*e);
}

int main()
{
    int T;
    cin>>T;
    while(T--)
    {
        V.clear();
        int n,k;
        sc2(n,k);

        for(int i=1;i<=n;i++){
            scanf("%lld%lld",&x[i],&y[i]);
        }

        for(int i=1;i<=n-2;i++)
        {
            for(int j=i+1;j<=n-1;j++){
                for(int p=j+1;p<=n;p++){
                    ll ans=solve(x[i],y[i],x[j],y[j],x[p],y[p]);
                    if(ans) V.push_back(ans);
                }
            }
        }
        int nn=V.size();
        nth_element(V.begin(),V.begin()+nn-k,V.end());
        if(V[nn-k]%2)
        printf("%lld.50\n",V[nn-k]/2);
        else
        printf("%lld.00\n",V[nn-k]/2);
    }
    return 0;
}