论文笔记《Data Uncertainty Learning in Face Recognition》
Data Uncertainty Learning in Face Recognition
- 2021.5.25
- CVPR20
Abstract
- 对于有噪声的图片,对于数据的不确定性非常重要,但很少有研究面部识别。之前的PFE将每个面部的嵌入作为高斯分布来考虑不确定性。它使用先前已有模型的固定特征作为高斯分布的均值,并通过一种特殊昂贵的度量方法预测方差,所以这个方法使用起来并不方便,并不确定该不确定性是怎么影响特征学习的。本工作将数据不确定学习用到了面部识别上,特征(均值)和不确定性(方差)可以首次同时进行学习。我们还对不确定性估计如何帮助减少噪声样本的不利影响以及如何影响特征学习进行了深入的分析。
Introduction
-
数据不确定性捕获了数据内在的噪声,因为噪声是广泛存在于图片的,所以对这样的不确定性进行建模非常重要
![]()
-
大多数人脸识别方法将每个脸的图片表示为潜在空间一个确定点的嵌入。通常,相同ID的高质量图片可以进行聚类。然后,很难为带噪声的人脸图片预测一个准确的点的嵌入,这些点通常在聚类之外。
-
在PFE中,给定一个训练好的FR模型,高斯分布对于每个样本的的均值固定为模型的嵌入,一个额外的分支加入这个模型来训练预测方差,这个训练通过相似度的度量方式驱动,MLS,预测两个高斯分布之间的相似概率。可以看到PFE对高质量的样本预测出小方差,对于有噪声的预测出大的方差,从而减少对噪声样本的错误匹配。所以,并不清楚不确定性对于特征学习产生的影响。而且传统意义上的cos相似度并不可以用,而是用复杂的MLS进行代替,产生更多的时间和内存开销
-
这是第一次提出在人脸识别中运用数据不确定学习,将特征和不确定性,也就是均值和方差同时进行学习。可以让同类样本更加紧凑,不同类的样本更加分离。这样,可以使用传统的cos相似度进行度量,不再需要MLS
-
具体而言,我们提出了两种措施
- 首先是基于分类的,从零开始学习模型
- 第二种是基于回归的,改进现存的已有模型
-
我们将讨论学习得到的不确定性在这两种方法下对于模型训练有多大影响,我们得到一个结论就是。学习得到的不确定性会通过自适应的减少噪声样本带来的负面影响来改善相同嵌入的学习。其最后的实验结果在多个确定性模型上都有所提升,尤其是在低质量图片的benchmark上效果会很好,表明数据不确定学习对于非结构化的人脸识别场景更为适用。
-
我们的方法并不是专门针对有噪声的数据训练提出的,但是我们从图像噪声的角度对学习到的数据不确定性如何影响模型训练进行了有意义的分析。验结果表明,本文提出的方法在噪声数据集上具有更高的鲁棒性。
Method
Preliminaries
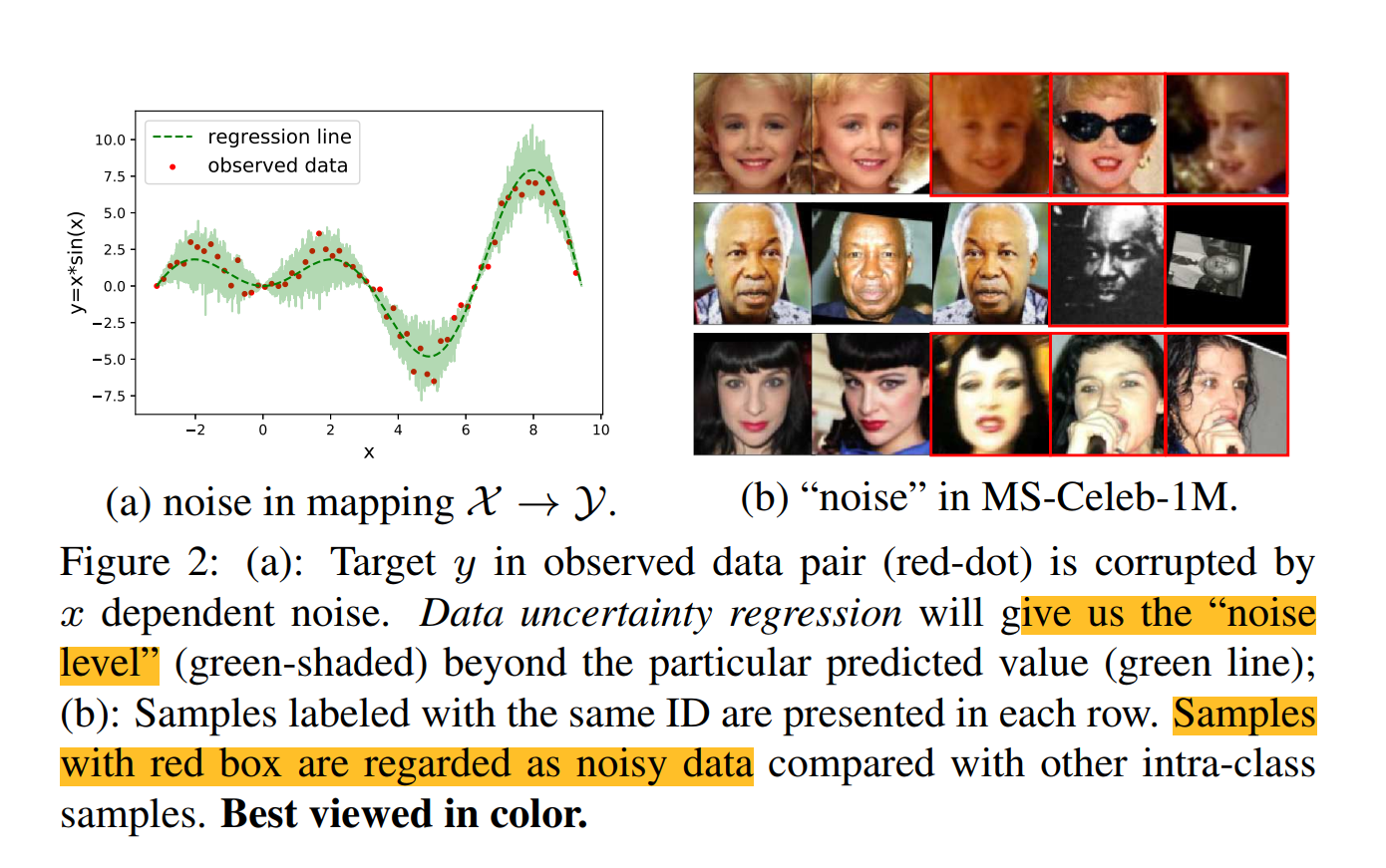
- 假设在连续的映射空间中\(\cal{X}\rightarrow \cal{Y}\),每个\(y_i\in\cal{Y}\)被一些输入以来的噪声破坏,记为\(n(x_i),x_i\in\cal{X}\),考虑一个见到的情况,这个噪声是额外从均值为0和与\(x\)相关的方差中得到的,可以将观察目标表示成\(y_i=f(x_i)+\epsilon\sigma(x_i),\epsilon\sim\mathcal{N}(0,\mathbf{I})\),传统的回归任务只根据输入预测embedding,有数据不确定性学习的回归模型也会预测方差\(\sigma(x_i)\),表示预测值的不确定性
- 在人脸数据中的不确定性。网上收集的大量人脸图像在视觉上具有模糊性,很难从训练集中筛选出这些质量较差的样本,在深度学习时代,每个样本都被表示为潜在空间中的一个嵌入。如果我们假设每个\(x_i\in\cal{X}\)有理想的嵌入并不受任何身份无关信息的影响,可以将网络所预测的DNN重新描述成\(z_i=f(x_i)+n(x_i)\)
Classification-based DUL
- 分布表征。我们将潜在空间内的每个样本\(x_i\)的表征\(z_i\)定义为高斯分布\(p(z_i|x_i)=\mathcal{N}(z_i;\mu_i,\sigma_i^2 I)\)高斯分布均值和方差两个参数都是输入依赖的,\(\mu_i=f_{\theta_1}(x_i)\)表示练的特征,\(\sigma_i=f_{\theta_2}(x_i)\)表示预测的不确定性,其中\(\theta_1,\theta_2\)分别代表的是模型参数,这里我们想到预测的高斯分布是对角多元正态分布。现在每个样本的表征不再是一个确定的嵌入点而是一个\(\mathcal{N}(z_i;\mu_i,\sigma_i^2 I)\)中随机采样的嵌入。但是采样是不可导的会导致不可反向传播,我们使用重参数技巧让模型正常使用梯度。具体的,我们首先从一个普通的分布中采样一个随机的噪声\(\epsilon\),独立于模型参数,生成\(s_i\)作为等效采样,有\[s_i=\mu_i+\epsilon\sigma_i,\ \epsilon\sim\mathcal{N}(0,I) \]
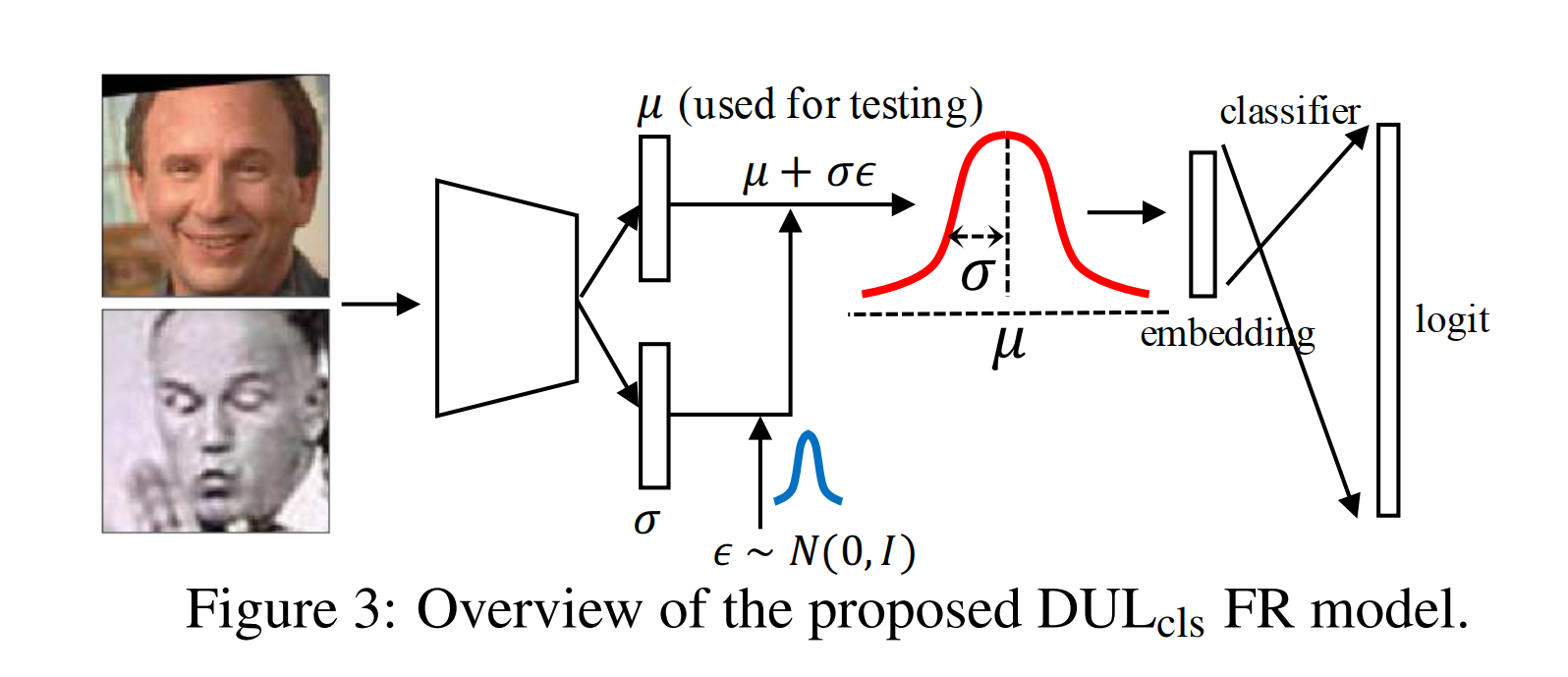
-
分类损失。因为\(s_i\)是每个图片\(x_i\)的最终表征,我们将其放入分类其中最小化下面的softmax loss
\[L_{softmax}=\frac{1}{N}\sum_i^N-log\frac{e^{w_{y_i}s_i}}{\begin{matrix} \sum_{c}^C e^{w_{c}s_i} \end{matrix}} \] -
上述公式表示所有的嵌入都在训练阶段被方差\(\sigma_i\)所影响,这会导致模型对于所有样本都预测比较小的\(\sigma\),为了抑制其中不稳定成分,这样其实这个随机表征会逐渐退化成原始确定性表征。也让上面的loss为所有样本预测很难收敛,受变分信息瓶颈的启发,我们在优化过程中为了限制\(\mathcal{N}(\mu_i,\sigma_i)\)接近一个正常分布\(\mathcal{N}(0,I)\)设置了一个正则项,通过KL散度进行计算,可以描述成
\[L_{kl}=KL[N(z_i|\mu_i,\sigma_i^2)||N(\epsilon|0,I)]=-\frac{1}{2}(1+log\sigma^2-\mu^2-\sigma^2) \] -
上面的两个loss起到了互相制约的作用,最后的loss采用\(L_{cls}=L_{softmax}+\lambda L_{kl}\)
Regression-based DUL
-
人脸数据集中的映射空间由连续的图像空间\(\mathcal{X}\)和离散的对应标签\(\mathcal{Y}\),并不可以直接通过数据不确定性回归来拟合,关键之处在于身份标签\(y_c\in Y\)不可以做为连续的目标向量来估计,所以我们需要解决这一问题
![]()
-
为人脸识别构造新的映射空间,我们构造了一个新的目标空间,对于人脸数据来说连续,最重要的是,它几乎等同于原始的离散目标空间\(Y\),这鼓励了正确的映射关系。尤其是,我们预训练好了一个确定性模型,我们利用其分类器中的权重\(\mathcal{W}\in\mathbb{R}^{D\times C}\)作为目标向量,其中每一个\(w_i\in\mathcal{W}\)都可以作为相同类别嵌入的典型中心,\(\{\mathcal{X,W}\}\)被看作是我们新的等价映射空间。与连续映射空间内的不确定性相似,这个空间内也含有固有的噪声,我们可以将其映射描述成\(w_i=f(x_i)+n(x_i)\)
-
之后我们就可以通过数据不确定性回归预测上面的\(f\)和\(n\),具体的一个高斯分布可以被假设成如下的似然函数:\(p(z_i|x_i)=\mathcal{N}(z_i;\mu_i,\sigma_i^2I)\),如果我们将每个\(w_c\)作为目标,我们需要最大化下面对于每个\(x_i\)的似然
\[p(w_c|x_{i\in c},\theta)=\frac{1}{\sqrt{2\pi\sigma_i^2 }}exp(-\frac{(w_c-\mu_i)^2}{2\sigma_i^2}) \] -
对此求对数似然
\[\mathrm{ln} p(w_c|x_{i\in c},\theta)=-\frac{(w_c-\mu_i)^2}{2\sigma_i^2}-\frac{1}{2}\mathrm{ln}\sigma^2_i-\frac{1}{2}\mathrm{ln}2\pi \] -
假设\(x_i,i\in1,2,...\)是独立同分布的,在所有数据集上的似然为\(\prod_c\prod_i\mathrm{ln} p(w_c|x_{i\in c},\theta)\)实际中我们训练网络来预测log方差\(r_i:=\mathrm{ln}\sigma_i^2\)来在随机优化过程中稳定数值解。最后将这个最大似然转换成下面函数的最小,其中\(D\)表示嵌入的维度,\(C\)表示类别数,\(N\)表示数据量,\(l\)表示每个向量中的第\(l\)维
\[\mathcal{L}_{rgs}=\frac{1}{2N}\sum_c^C\sum_{i\in c}[\frac{1}{D}\sum_l^Dexp(-r_i^{(l)})(w_c^{(l)}-\mu_i^{(l)})^2+r_i^{(l)}] \] -
**Loss Attenuation Mechanism **通过上面的分析,我们所学习得到的方差\(\sigma_i\)可以被认为是衡量所学习得到的嵌入\(\mu_i\)属于第\(c\)类的不确定性得分。具体来说,对于这些离类别中心\(w_c\)比较远的模棱两可的\(\mu_i\),将估计较大的方差来缓和误差项\(\frac{(w_c-\mu_i)^2}{2\sigma_i^2}\)来防止对有噪声样本的过拟合。回归DUL不鼓励给所有样本预测大方差,这可能会导致\((w_c-\mu_i)^2\)拟合不足,并且较大的\(\sigma\)项会反过来惩罚模型。同时它也不鼓励给所有样本预测小方差,可能会导致误差项呈指数增长。所以,这可以误差项自适应调节。这使得模型学会了减弱由于一些质量不高的样本导致的摸棱两可的\(\mu_i\)
Discussion
- 首先讨论\(DUL_{cls}\)与VIB之间的关系,VIB是在深度学习框架下对信息瓶颈(IB)原理的一种变分近似,VIB寻求从输入数据X到潜在表征空间Z的随机映射,找到使Z尽可能简洁但仍有足够能力预测标签Y之间进行基本的权衡,可以发现\(L_{cls}\)与VIB相似,但我们是从数据不确定性的角度分析而VIB是通过信息瓶颈的角度分析
- 我们接着阐述一些\(DUL_{rgs}\)与PFE之间的不同,尽管PFE和\(DUL_{rgs}\)都将输入的不确定性作为方差的表征。然后,PFE衡量的是每个正样本对\(\{x_i,x_j\}\)具有相同潜在嵌入的最大似然,而\(DUL_{rgs}\)将一个传统的最小二乘回归技术几十位具有数据不确定性回归模型的最大似然估计。最后,\(DUL_{cls}\)和\(DUL_{rgs}\)都学习了身份表征\(\mu\)和不确定性表示\(\sigma\),确保我们的预测可以直接用常用的匹配度量进行评价。而PFE中用来一个相互似然得分(MLS)来作为度量方法改进确定性模型的表现,因为身份表征并没有学习。
Experiment
Implement details
- baseline先用ResNet+SE-block,主干网络投影头的结构为\(BackBone-Flatten-FC-BN\),嵌入维度为512
- \(DUL_{cls}\)有一个额外的分支来输出方差,和上面结构相同
- \(DUL_{rgs}\)也有一个额外的投影头分支,其结构为\(BackBone-Flatten-FC-BN-ReLU-FC-BN-exp\)来输出方差
Training
- baseline模型和\(DUL_{cls}\)模型都训练了210000次,用一个SGD优化器和0.9的动量,……
- 对于\(DUL_{rgs}\),我们首先训练了baseline模型210000个step,然后再所有的卷积层固定参数。然后我们训练均值和方差的分支额外140000个step。
Comparing DUL with Deterministic Baselines
-
所有的主干模型都用ResNt18训练,带有不同的softmax损失,嵌入的特征和分类器中的权重都经过L2归一化。表中展示的结果当然是比之前的确定模型性能都要好。采用余弦相似度进行评价。这些结果表明身份嵌入(µ)用数据不确定性训练(σ)比基准模型估计的点嵌入具有更好的类内紧性和类间可分性。
-
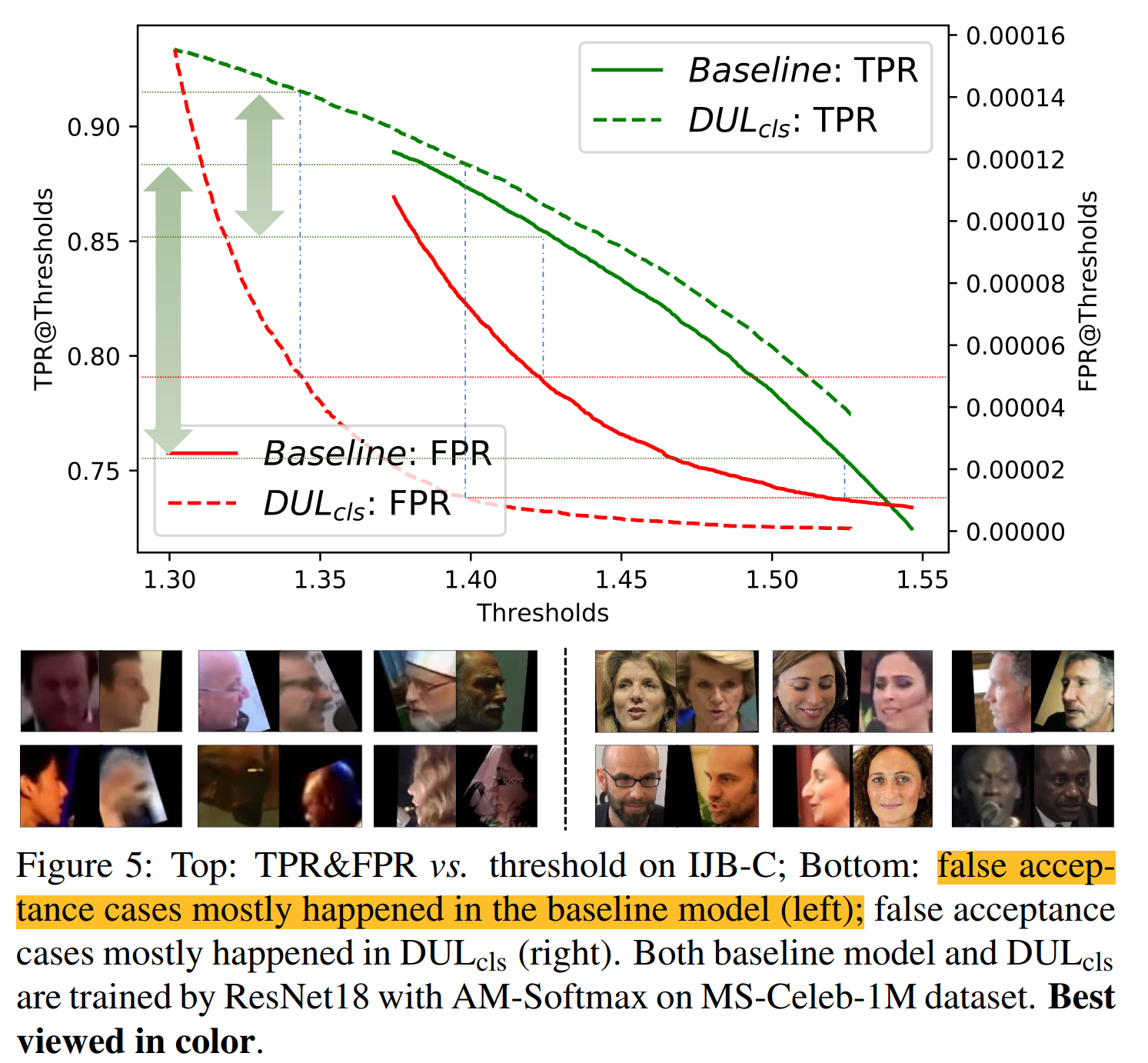
所提出的DUL在IJB-C基准测试验证协议上取得了最显著的改进,也是最具挑战性的改进。因此,我们绘制了真实接受率(TPR)和错误接受率(FPR)随不同匹配阈值变化的曲线。我们可以看到,\(DUL_{cls}\)解决了更多带有极端噪声的FP情况,这通常发生在基线模型中。这表明数据不确定性学习模型比确定性模型更适用于无约束的人脸识别场景。
(这里阈值是什么还没弄懂)
![]()
Comparing DUL with PFE & SOTA
- 略
Understand Uncertainty Learning
-
**What is the meaning of the learned uncertainty? **
-
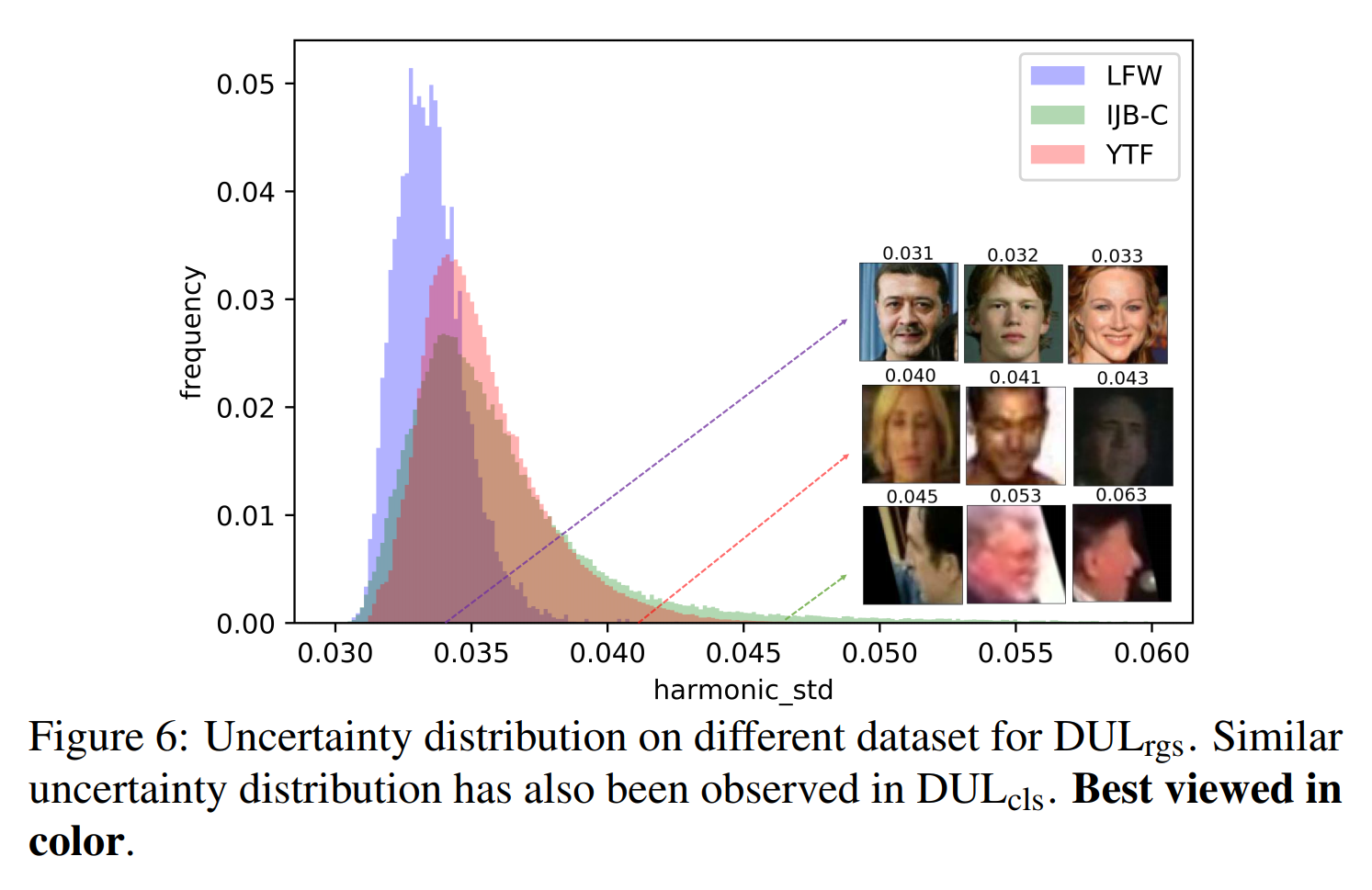
所预测的不确定性和人脸图片的质量联系很紧密。对于可视化,我们展示了学习得到的不确定性,如图6所示,结果表明,学习的不确定性随着图像质量的下降而增加。这种学习的不确定性可以看作是模型估计的相应身份嵌入的质量,衡量预测的人脸表示与潜在空间中真实(或真实)点位置的接近程度。
![]()
-
因此,利用数据不确定性学习进行人脸识别有两个优点。首先,学习到的方差可以作为一个“风险指标”来警告FR系统,当估计方差很高时,输出决策是不可靠的。其次,学习的方差也可以作为图像质量评价的度量。在这种情况下,我们注意到没有必要像以前那样训练一个单独的质量评估模型,它需要明确的质量标签。
-
-
**How the learned uncertainty affect the FR model? **
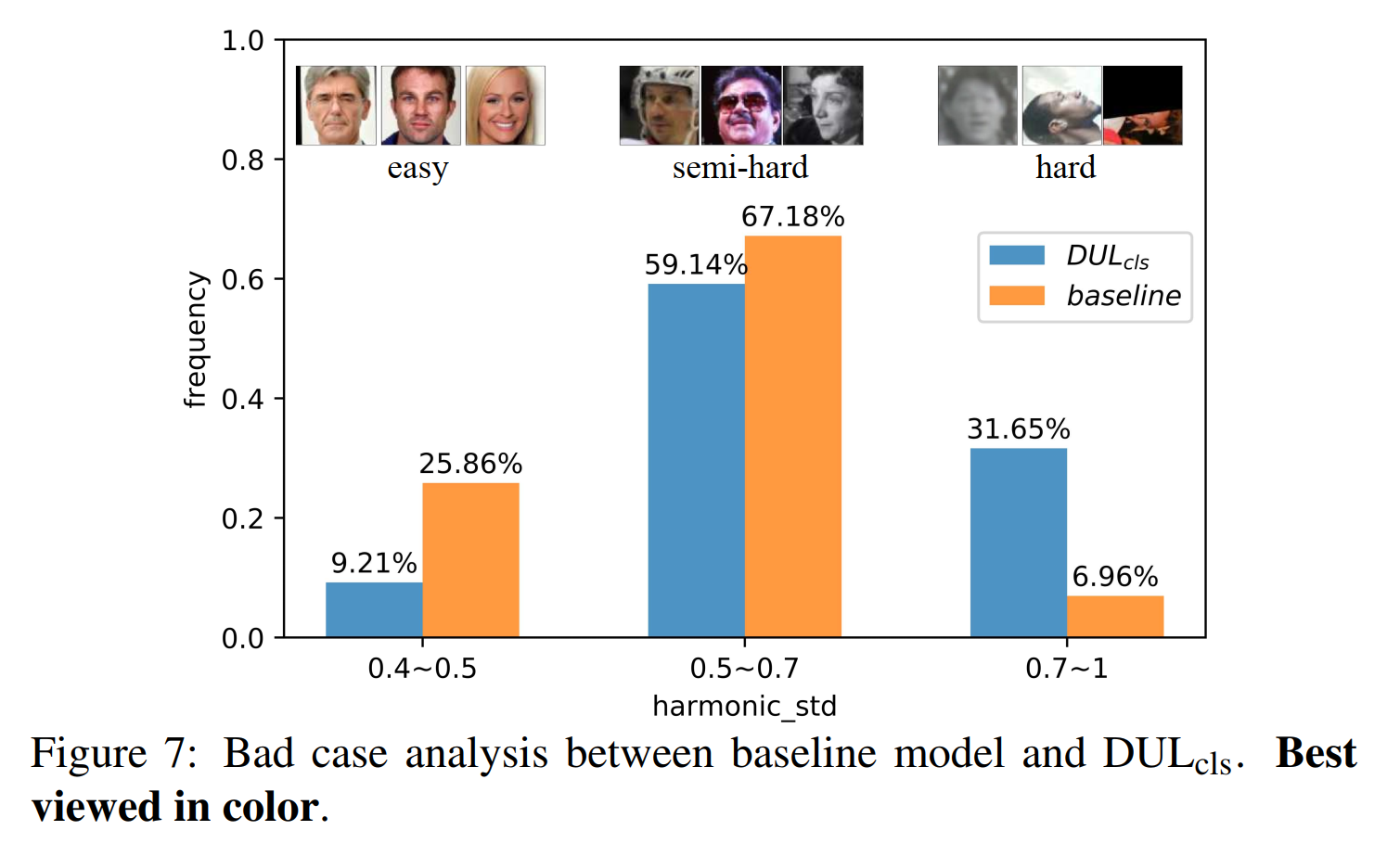
- 我们将MS-Celeb-1M中的样本根据\(DUL_{cls}\)分成三个类别,方差较低的简单样本,中等方差的一般样本,方差较大的难样本。我们计算了三种类别所有被错误分类样本的各种比例,与basline模型相比,我们的\(DUL_{cls}\)在简单样本和一般样本上造成的错误较少,较难的样本上还是原baseline模型做的好。这证明了具有数据不确定性学习的网络更关注于那些需要正确分类的样本,同时放弃了那些过度难的样本并没有去过度拟合它们。我们也在\(DUL_{rgs}\)上做出了相似的实验,我们计算了baseline模型和\(DUL_{rgs}\)模型类别中心点\(w_c\)和类内身份嵌入之间的平均欧氏距离。如图8所示,可以看到,\(DUL_{rgs}\)将简单样本和一般样本向他们的类别中心拉近了将难样本拉远,这也就说明了其通过自适应调整权重的方式防止模型对于极度有噪声的样本过拟合。
![]()
-
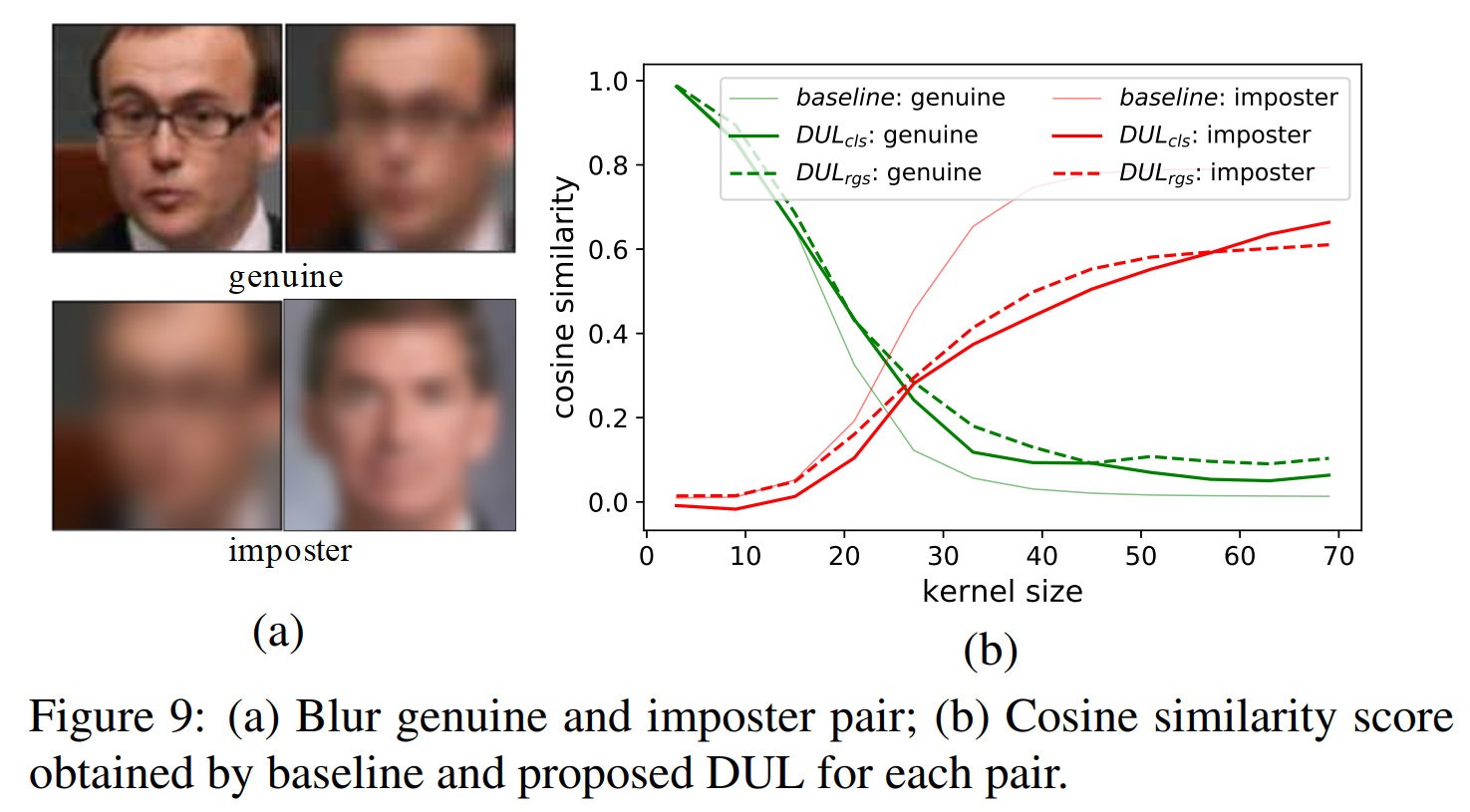
最后我们手动构造了不同blur下的假冒/真实测试样本对,来分别比较我们主干模型和我们的方法之间的余弦相似度,如图9所示,可以看到随着blur噪声的增加,我们的baseline和所提出的DUL模型均会有很大的下降。但是我们所提出的方法真实数据对的相似性更好,假冒对更低,说明我们的方法更鲁棒。
![]()
Conclusion
- 其实这是一篇去年的文章了,它提出了两种在人脸识别上的数据不确定学习方法,对每个图片给出了一种高斯分布的预测结果,将原身份嵌入作为均值,将其不确定性学习为方差。证明其效果更好,可以减少模型在噪声较多的复杂样本上的过拟合,比确定性模型好也更具有鲁棒性。也额外讨论了这个不确定性如何从图片噪声角度影响模型训练。其中有一个结论在于,对于其预测的方差,可以根据这个方差来判断样本的难易程度判断出是简单样本还是一般样本还是复杂样本。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号