java常用数据结构
java常用数据结构:数组、链表、栈、队列、二叉树、红黑树、哈希表.......!
数组
数组是相同类型变量的结合，可以通过下标来访问数组，数组占用连续的内存空间，这样在检索时能够快速地通过偏移来进行下标定位索引数据。数组在初始化之后内存大小将不能被改变。数组分一维数组和二维数组，二维数组其实也是一维数组，是一个一维数组中引用啦另一个一维数组。
链表
单向链表
单链表的存储原理图，简单易懂，head为头节点，他不存放任何的数据，只是充当一个指向链表中真正存放数据的第一个节点的作用，而每个节点中都有一个next引用，指向下一个节点，就这样一节一节往下面记录，直到最后一个节点，其中的next指向null。
双向链表
如果我们在表的第一项处插入或者删除元素该操作花费的时间很短，但是如果我们需要在最后一项插入或者删除元素这是一个花费时间的操作。
我们可以用双向链表来解决这个问题。双向链表的每一个结点都有一条指向其后继结点的next链和一条指向其前结点的pre链。双向链表既可以从第一项开始遍历也可以从最后一项开始往前遍历，双向链表可以用上图表示：
栈
栈是一种只允许在一端进行插入或删除的线性表，也就是说先进后出。栈的操作端通常被称为栈顶，另一端被称为栈底，栈的插入操作称为压栈（push），栈删除操作称为出栈（pop）。压栈是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；出栈则是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。
栈的实现方式主要分为两种，一种是基于数组实现的，另一种则是基于链表。顺序存储的栈称为顺序栈；链式存储的栈称为链式栈。不管是基于何种形式，一般都要实现几个方法，分别为检查栈是否为空，是否已满，压栈操作和出栈操作，值得说明的是，在链式栈中无需检测栈是否已满，只要内存足够大，原理上链式栈是不会满的。
队列
队列（queue）：一种只允许在一端进行插入，在另一端进行删除的线性表结构。允许插入的一端叫队尾（rear），允许删除的一端叫队头（font）。
二叉树
二叉树：树的每个节点最多只能有两个子节点，如果有两个以上就不叫二叉树，被称为多路树。
查找节点
查找某个节点，我们必须从根节点开始遍历。
①、查找值比当前节点值大，则搜索右子树；
②、查找值等于当前节点值，停止搜索（终止条件）；
③、查找值小于当前节点值，则搜索左子树；
遍历完整个树没找到，返回null
插入节点
要插入节点，必须先找到插入的位置。与查找操作相似，由于二叉搜索树的特殊性，待插入的节点也需要从根节点开
始进行比较，小于根节点则与根节点左子树比较，反之则与右子树比较，直到左子树为空或右子树为空，则插入到相应为
空的位置，在比较的过程中要注意保存父节点的信息 及 待插入的位置是父节点的左子树还是右子树，才能插入到正确的
位置。
遍历树
遍历树是根据一种特定的顺序访问树的每一个节点。比较常用的有前序遍历，中序遍历和后序遍历。而二叉搜索树最常用的
是中序遍历。
①、中序遍历:左子树——》根节点——》右子树
②、前序遍历:根节点——》左子树——》右子树
③、后序遍历:左子树——》右子树——》根节点
查找最大值和最小值
这没什么好说的，要找最小值，先找根的左节点，然后一直找这个左节点的左节点，直到找到没有左节点的节点，那
么这个节点就是最小值。同理要找最大值，一直找根节点的右节点，直到没有右节点，则就是最大值。
删除节点
删除节点是二叉搜索树中最复杂的操作，删除的节点有三种情况，前两种比较简单，但是第三种却很复杂。
1、该节点是叶节点（没有子节点）
2、该节点有一个子节点
3、该节点有两个子节点
①、删除没有子节点的节点
要删除叶节点，只需要改变该节点的父节点引用该节点的值，即将其引用改为 null 即可。要删除的节点依然存
在，但是它已经不是树的一部分了，由于Java语言的垃圾回收机制，我们不需要非得把节点本身删掉，一旦Java意识
到程序不在与该节点有关联，就会自动把它清理出存储器。
删除节点，我们要先找到该节点，并记录该节点的父节点。在检查该节点是否有子节点。如果没有子节点，接着
检查其是否是根节点，如果是根节点，只需要将其设置为null即可。如果不是根节点，是叶节点，那么断开父节点和
其的关系即可。
②、删除有一个子节点的节点
删除有一个子节点的节点，我们只需要将其父节点原本指向该节点的引用，改为指向该节点的子节点即可。
③、删除有两个子节点的节点
当删除的节点存在两个子节点，那么删除之后，两个子节点的位置我们就没办法处理了。既然处理不了，我们就
想到一种办法，用另一个节点来代替被删除的节点，那么用哪一个节点来代替呢？
我们知道二叉搜索树中的节点是按照关键字来进行排列的，某个节点的关键字次高节点是它的中序遍历后继节
点。用后继节点来代替删除的节点，显然该二叉搜索树还是有序的。（这里用后继节点代替，如果该后继节点自己也
有子节点，我们后面讨论。）
那么如何找到删除节点的中序后继节点呢？其实我们稍微分析，这实际上就是要找比删除节点关键值大的节点集
合中最小的一个节点，只有这样代替删除节点后才能满足二叉搜索树的特性。
后继节点也就是：比删除节点大的最小节点。
算法：程序找到删除节点的右节点，(注意这里前提是删除节点存在左右两个子节点，如果不存在则是删除情况的前
面两种)，然后转到该右节点的左子节点，依次顺着左子节点找下去，最后一个左子节点即是后继节点；如果该右节
点没有左子节点，那么该右节点便是后继节点。
需要确定后继节点没有子节点，如果后继节点存在子节点，那么又要分情况讨论了。
①、后继节点是删除节点的右子节点
这种情况简单，只需要将后继节点表示的子树移到被删除节点的位置即可！
②、后继节点是删除节点的右子节点的左子节点
④、删除有必要吗？
通过上面的删除分类讨论，我们发现删除其实是挺复杂的，那么其实我们可以不用真正的删除该节点，只需要在
Node类中增加一个标识字段isDelete，当该字段为true时，表示该节点已经删除，反正没有删除。那么我们在做比如
find()等操作的时候，要先判断isDelete字段是否为true。这样删除的节点并不会改变树的结构。
红黑树
特征:
①、节点都有颜色；
②、在插入和删除的过程中，要遵循保持这些颜色的不同排列规则。
第一个很好理解，在红-黑树中，每个节点的颜色或者是黑色或者是红色的。当然也可以是任意别的两种颜色，这里的颜色用于标
记，我们可以在节点类Node中增加一个boolean型变量isRed，以此来表示颜色的信息。
第二点，在插入或者删除一个节点时，必须要遵守的规则称为红-黑规则：
1.每个节点不是红色就是黑色的；
2.根节点总是黑色的；
3.如果节点是红色的，则它的子节点必须是黑色的（反之不一定）,(也就是从每个叶子到根的所有路径上不能有两个连续的红
色节点)；
4.从根节点到叶节点或空子节点的每条路径，必须包含相同数目的黑色节点（即相同的黑色高度）。
从根节点到叶节点的路径上的黑色节点的数目称为黑色高度，规则 4 另一种表示就是从根到叶节点路径上的黑色高度必须相
同。
注意：新插入的节点颜色总是红色的，这是因为插入一个红色节点比插入一个黑色节点违背红-黑规则的可能性更小，原因是插入
黑色节点总会改变黑色高度（违背规则4），但是插入红色节点只有一半的机会会违背规则3（因为父节点是黑色的没事，父
节点是红色的就违背规则3）。另外违背规则3比违背规则4要更容易修正。当插入一个新的节点时，可能会破坏这种平衡
性，那么红-黑树是如何修正的呢？
红-黑树的自我修正
红-黑树主要通过三种方式对平衡进行修正，改变节点颜色、左旋和右旋。
①、改变节点颜色
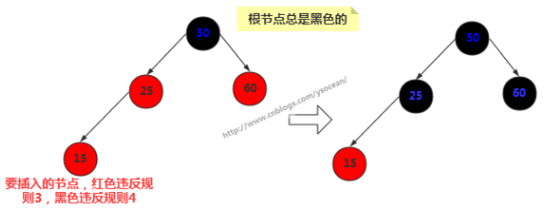
新插入的节点为15，一般新插入颜色都为红色，那么我们发现直接插入会违反规则3，改为黑色却发现违反规则4。这时
候我们将其父节点颜色改为黑色，父节点的兄弟节点颜色也改为黑色。通常其祖父节点50颜色会由黑色变为红色，但是由
于50是根节点，所以我们这里不能改变根节点颜色。
②、右旋
首先要说明的是节点本身是不会旋转的，旋转改变的是节点之间的关系，选择一个节点作为旋转的顶端，如果做一次右
旋，这个顶端节点会向下和向右移动到它右子节点的位置，它的左子节点会上移到它原来的位置。右旋的顶端节点必须要
有左子节点。
③、左旋
左旋的顶端节点必须要有右子节点。
我们改变颜色也是为了帮助我们判断何时执行什么旋转，而旋转是为了保证树的平衡。光改变节点颜色是不能起到任何作
用的，旋转才是关键的操作，在新增节点或者删除节点之后，可能会破坏二叉树的平衡，那么何时执行旋转以及执行什么
旋转，这是我们需要重点关注的。
