数据结构-B树和B+树

一、B树

1.B树的定义

B树就是一棵平衡的多叉查找树

2.B树的作用以及相对于二叉查找树的优势

用于实现快速查找，相对于二叉树，具有更多的分支，更小的高度。查找树的高度决定了查找过程中访问磁盘的次数，而磁盘的访问速度低。由于B树具有更小的高度，因此在查找时对磁盘的访问会大大降低，从而相对于二叉查找树有更高的效率

3.B树的特性

一棵M阶的B树的特性：

1）数据项存储在树叶上

2）非叶子节点存储M-1个关键字，这些关键字用于指示搜索的方向；第i个关键字为第i+1棵子树中最小的关键字

3）树根节点和树叶儿子数在2到M之间，除树根和叶子节点外，其他节点儿子数在M/2 到M 之间

4）所有树叶都在相同深度上并有L/2 到L之间个数据项

每个树节点代表一个磁盘区块，因此根据磁盘区块的大小和所存储项的大小决定M和L的值。假设一个区块为8192个字节，一棵M阶B数非叶子节点有M-1个关键字和M个指向子节点的指针，设每个关键字占用32个字节，每个指针4个字节，则一个非叶子节点占用36M-32字节，这样可以出M=288。设每个记录占用256个字节，则可计算出L=32

M=5, L=5 的B树结构图：

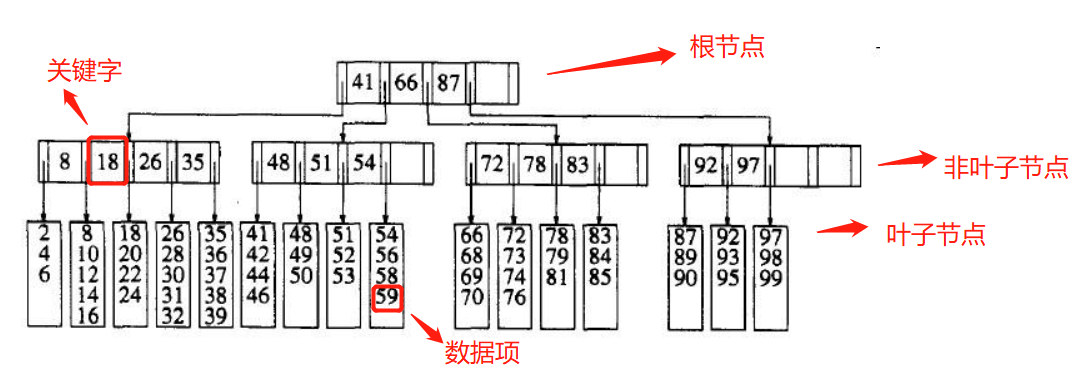
 4.对B数的操作

4.1插入

如要将57插入上面的B树中，首先沿树的根节点向下查找，发现57不在树中，且该树叶没有装满，则直接添加，如

 

 

 如果节点中数据项已经满了，则将这个节点分裂成两个节点，如在上图基础上再添加55节点，则需要将叶子节点分裂为两个，并更新父节点，可以看到新增的叶子节点都为3个数据项，满足数据项在L/2到L之间的要求：

 

 

 

 上面的分裂后会是父节点新增一个子节点，如果父节点的字节点没满则没问题，如果父节点已经满了呢。解决方法是继续向上分裂父节点，直到找到一个不需要分裂的父节点。如果分裂到了树根则分裂完后有两个树根，两个树根是不能接受的，这时可以新增一个根节点，根节点下为前面分裂后的两个树根节点，这是B树高度增加的唯一方式。此时树根只有两个子节点，这就是为什么根节点允许只有两个子节点的原因。将40插入到上面的树中需要分裂父节点：

 

 

 

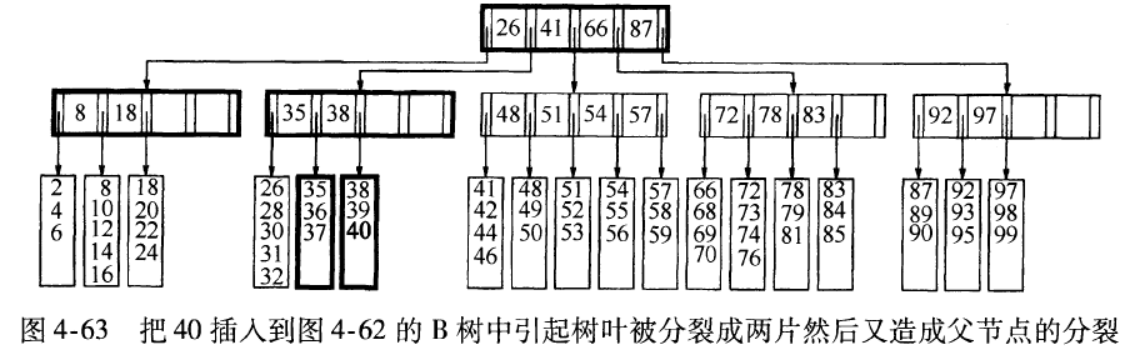
 4.2 删除

1）从上到下找到需要删除的数据项

2）删除数据项

3）由于删除数据项后，当前节点数据项数减小，如果数据项数不小于最小值（L/2）则直接结束，如果删除后小于最小值，则需要调整数结构。此时，如果临节点数据项数大于最小值，则从这个临节点领养一个。如果临节点已经达到最小值，则将当前节点和临节点合并为一个节点。这样他们的父节点将少一个节点，如果父节点的子节点数又小于最小值，则按同样的方法领养或合并节点，直到树达到要求。这个过程可以一直上行到根，到根节点时可能导致根节点只有一个儿子，此时删除根节点，将当前节点最为新的根，这是使B树高度降低的唯一方式。如在上面树基础上删除99：

 二、B+树

B+树是B树的一个升级版，相对于B树来说B+树更充分的利用了节点的空间，让查询速度更加稳定

B+树和B树的区别：

（1）B+跟B树不同在于B+树的非叶子节点不保存关键字记录的指针，只进行数据索引，这样使得B+树每个非叶子节点所能保存的关键字大大增加；
（2）B+树叶子节点保存了父节点的所有关键字记录的指针，所有数据地址必须要到叶子节点才能获取到。所以每次数据查询的次数都一样；

优缺点：

1、B+树的层级更少：相较于B树B+每个非叶子节点存储的关键字数更多，树的层级更少所以查询数据更快；

2、B+树查询速度更稳定：B+所有关键字数据地址都存在叶子节点上，所以每次查找的次数都相同所以查询速度要比B树更稳定;

3、B+树天然具备排序功能：B+树所有的叶子节点数据构成了一个有序链表，在查询大小区间的数据时候更方便，数据紧密性很高，缓存的命中率也会比B树高。
4、B+树全节点遍历更快：B+树遍历整棵树只需要遍历所有的叶子节点即可，，而不需要像B树一样需要对每一层进行遍历，这有利于数据库做全表扫描。

B树相对于B+树的优点是，如果经常访问的数据离根节点很近，而B树的非叶子节点本身存有关键字其数据的地址，所以这种数据检索的时候会要比B+树快。

注：上面B树和B+树的资料来源两个地方，根据B+树的介绍，感觉上面的B树就是B+树，不过两者区别，可以总结为一点：B树的非叶子节点包含数据索引，而B+树只有叶子节点才有数据索引，查找时必须要找到叶子节点。