简析算法中的时间复杂度与空间复杂度

前言：算法复杂度是什么？什么作用？为什么？本文将从这三个方面展开讨论。

 

一、时间复杂度与空间复杂度是什么？

任何程序运行都需要耗费计算机资源，算法的复杂性体现在运行该算法时的计算机所需资源的多少上，计算机资源最重要的是时间和空间（即寄存器）资源，因此复杂度分为时间复杂度和空间复杂度。

时间复杂度和空间复杂度往往是相互影响的。当追求一个较好的时间复杂度时，可能会使空间复杂度的性能变差，即可能导致占用较多的存储空间；反之，当追求一个较好的空间复杂度时，可能会使时间复杂度的性能变差，即可能导致占用较长的运行时间

 

时间复杂度：

1、一个算法花费的时间与该算法中语句的执行次数成正比，也就是说执行次数越多，花费的时间越多。执行次数又称为语句频度或时间频度，记为T(n)。

2、一般情况下，算法中基本操作重复执行的次数是问题规模为n的某个函数，用T(n)表示，若有某个辅助函数f(n),使得当n趋近于无穷大时，T（n)/f (n)的极限值为非零的常数，则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n)),称O(f(n)) 为算法的渐进时间复杂度，简称时间复杂度（ ps:是字母O而不是数字0 ）

3、在时间频度不相同时，时间复杂度有可能相同，如T(n)=n2+3n+4与T(n)=4n2+2n+1它们的频度不同，但时间复杂度相同，都为O(n2)

 

空间复杂度：

1、算法在运行过程中临时占用的存储空间随算法的不同而异，有的算法只需要占用少量的临时工作单元，而且不随问题规模的大小而改变，我们称这种算法是“就地\"进行的，是节省存储的算法，有的算法需要占用的临时工作单元数与解决问题的规模n有关，它随着n的增大而增大，当n较大时，将占用较多的存储单元，例如快速排序和归并排序就属于这种情况。
2、一般情况下，算法中基本操作重复执行的次数是问题规模为n的某个函数，用S(n)表示，若有某个辅助函数f(n),使得当n趋近于无穷大时，S（n)/f (n)的极限值为非零的常数，则称f(n)是S(n)的同数量级函数。记作S(n)=O(f(n)),称O(f(n)) 为算法的渐进时间复杂度，简称时间复杂度（ ps:是字母O而不是数字0 ）

3、一个算法在计算机存储器上所占用的存储空间分为三部分，分别为存储算法本身所占用的存储空间、算法的输入输出数据所占用的存储空间、算法在运行过程中临时占用的存储空间，算法的输入输出数据所占用的存储空间是由要解决的问题决定的，是通过参数表由调用函数传递而来的，它不随本算法的不同而改变。存储算法本身所占用的存储空间与算法书写的长短成正比，要压缩这方面的存储空间，就必须编写出较短的算法。

 

二、什么作用

合理分配计算机资源

 

 

三、 常见的时间复杂度：

O(n)  :    时间复杂度为O(n)—线性阶，就代表数据量增大几倍，耗时也增大几倍。比如常见的遍历算法。

 

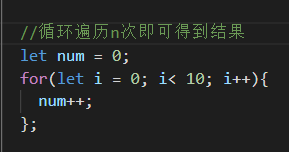
 O(n^2)   :     时间复杂度O(n^2)—平方阶, 就代表数据量增大n倍时，耗时增大n的平方倍，这是比线性更高的时间复杂度。比如冒泡排序，就是典型的O(n x n)的算法，对n个数排序，需要扫描n x n次。

 

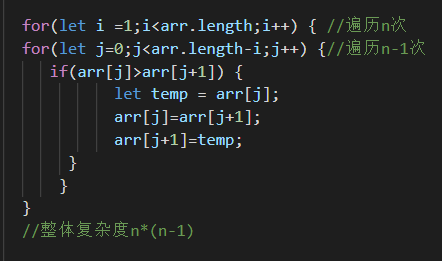
 O(logn)  ：   时间复杂度O(logn)—对数阶，当数据增大n倍时，耗时增大logn倍（这里的log是以2为底的，比如，当数据增大256倍时，耗时只增大8倍，是比线性还要低的时间复杂度）。二分查找就是O(logn)的算法，每找一次排除一半的可能，256个数据中查找只要找8次就可以找到目标。

如下例子，二分法实现indexOf方法(暂未对数组重复元素处理，仅当参考)

 

 

 

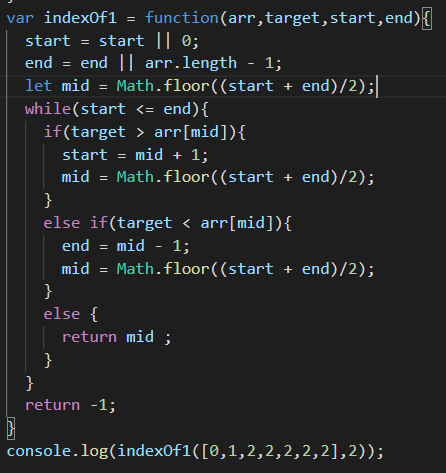
 O(nlogn)   ：   —线性对数阶，就是n乘以logn，当数据增大256倍时，耗时增大256*8=2048倍。这个复杂度高于线性低于平方。归并排序就是O(nlogn)的时间复杂度。

 

 

 

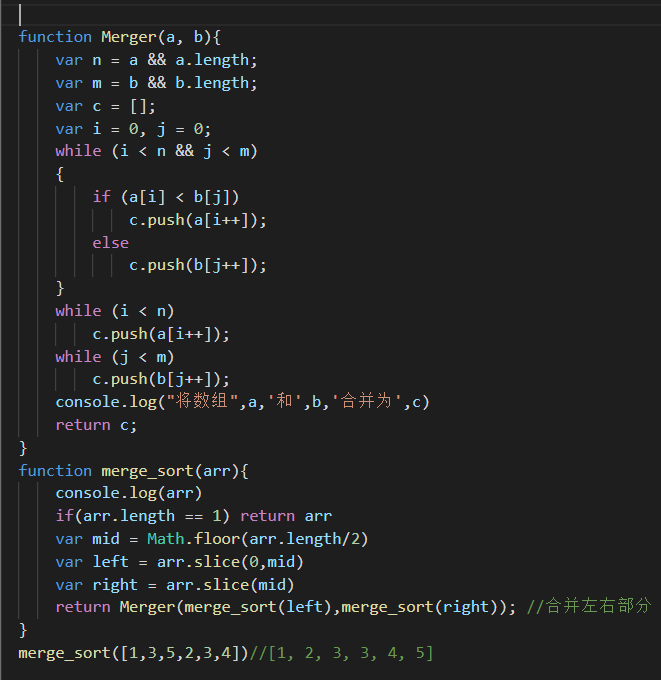
 O(1)   :   O(1)—常数阶：最低的时空复杂度，也就是耗时与输入数据大小无关，无论输入数据增大多少倍，耗时/耗空间都不变。 哈希算法就是典型的O(1)时间复杂度，无论数据规模多大，都可以在一次计算后找到目标。

 

 

时间复杂度的优劣对比
常见的数量级大小：越小表示算法的执行时间频度越短，则越优；

O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n3)

 

 

 

 

 

 

 

 

 

 

文章参考：

• https://blog.csdn.net/loongwong2011/article/details/52571513
• https://blog.csdn.net/A_dg_Jffery/article/details/99713579