20190919-6 四则运算试题生成,结对
本次作业要求参见:[https://edu.cnblogs.com/campus/nenu/2019fall/homework/7631]
结对伙伴:韩昊
• 功能1. 四则运算
支持出题4个数的四则运算题目,所有题目要求作者有能力正确回答
重难点:四个数字的四则运算,分两种优先级,加减与乘除,因此在计算表达式的时候,不能顺序处理。不过我想到了编译原理中,对于表达式的处理原理,因此借助了栈结构及逆波兰式的转换。
编程收获:本功能表面看起来简单,于是抬手就做,可是在实施时遇到了事先没有考虑到的问题,所以此处得出教训,在处理任何问题之前,需要多花些时间,进行详细的功能分析和设计,此处想到了一句话:“有的时候慢一点,往往会更快一点”。
重点代码片段:
# 将中缀表达式转换为后缀表达式 def middle_to_after(s): expression = [] ops = [] for item in s: if item in ['+', '-', '*', '/']: while len(ops) >= 0: if len(ops) == 0: ops.append(item) break op = ops.pop() if op == '(' or op_rules[item] > op_rules[op]: ops.append(op) ops.append(item) break else: expression.append(op) elif item == '(': ops.append(item) elif item == ')': while len(ops) > 0: op = ops.pop() if op == '(': break else: expression.append(op) else: expression.append(item) while len(ops) > 0: expression.append(ops.pop()) return expression
# 计算后缀表达式 def cal_suffix_exp_value(expression): stack_value = [] for item in expression: if item in ['+', '-', '*', '/']: n2 = stack_value.pop() n1 = stack_value.pop() result = cal_rules(n1, n2, item) stack_value.append(result) else: stack_value.append(int(item)) return stack_value[0]

• 功能2. 支持括号
重难点:此功能在功能1的基础上,增加了括号,思路上还是借助逆波兰式,但有个问题是如何保证随机生成的一对括号有意义,因此这里并不是真正意义上的随机,而是一种伪随机。
编程收获:这个地方的随机机制花费了很长时间去思考,最终伪随机借鉴了某些小游戏中的随机机制,所以收获是,平时还要多拓展自己的解决问题的思路,这样在考虑问题时才会更开阔。
重点代码片段:
# 4个数的式子括号最多两对,随机生成一对括号或两对括号 position_matrix = [[-1, 0, 0, 0, 1, 0, 0, 0, 0, 2, 2], [-1, 0, 0, 0, 0, 0, 1, 0, 0, 2, 2], [0, 0, -1, 0, 0, 0, 1, 0, 0, 2, 2], [0, 0, -1, 0, 0, 0, 0, 0, 1, 2, 2], [0, 0, 0, 0, -1, 0, 0, 0, 1, 2, 2], [-1, 0, 0, 0, 1, 0, -1, 0, 0, 0, 1], [-1, -1, 0, 0, 0, 1, 0, 0, 1, 0, 0], [-1, 0, 0, -1, 0, 0, 0, 1, 1, 0, 0], [0, 0, -1, -1, 0, 0, 0, 1, 0, 0, 1], [0, 0, -1, 0, 0, -1, 0, 0, 0, 1, 1] ] # 生成括号表达式 def generate_parentheses(self, exp): expression = [] # 从10种情况中选取一种 position = random.randint(0, 9) if exp: i = 0 for j in self.position_matrix[position]: if j == 0: expression.append(exp[i]) if i < len(exp): i += 1 elif j == -1: expression.append('(') elif j == 1: expression.append(')') # 如果生成的括号表达式形如 (1 + 2/3 + 3) 则重新生成 (1+(2+3))+4 1+((2+3)+4) 1+(2+(3+4)) if expression[0] == '(' and expression[-1] == ')': expression = self.generate_parentheses(exp) return expression return expression

[注]在实际代码中,我们将功能1和功能2结合到了一起,因此最终实现起来的结果是这样的:
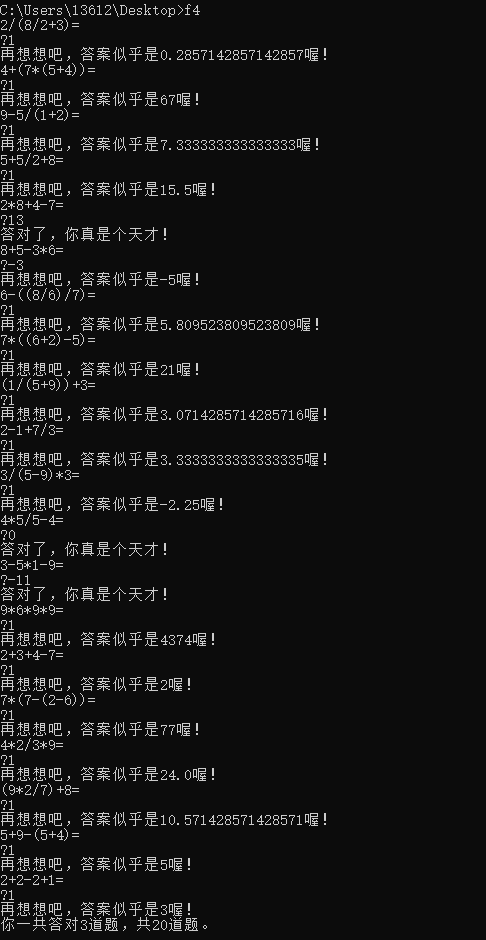
• 功能3. 限定题目数量,"精美"打印输出,避免重复
重难点:在前两个功能前提下,实现功能3相对来说比较简单,相对来说,重点是保证按参数指定的个数输出表达式及结果。编程收获:。
重点代码片段:
# 功能三输出一行计算表达式及结果 def print_exp_result(num): i = 0 num = int(num) while i < num: generate = Exp_Generator.Generator() mid_experision = generate.generate() suffix_expression = middle_to_after(mid_experision) value = cal_suffix_exp_value(suffix_expression) mid_experision += '=' print('%-15s %-15s' % (mid_experision, value)) i += 1
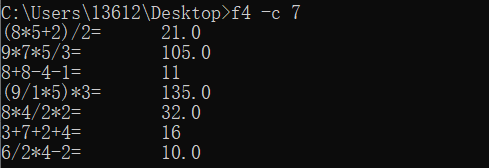
• 总结与体会
1、费时:
1.1 关于栈在四则运算的使用
由于对本科学习的数据结构内容有所遗忘,导致在该部分花费了一定时间,通过查阅教材,教程等等,由于逆波兰和栈的使用是重点所以遇到困难我们仍然坚持使用,最后慢慢摸索,实现了该功能。
1.2 研究如何避免生成重复问题
解决的办法在前文的文字和代码中已经有所体现,但在该部分确实花费了较多时间,我们通过积极思考,积极交流,最终找出当下的办法。
2、收获
2.1 关于结对编程:沟通太重要了,分工太重要了,真的要坐在一起编码,有问题随时交流,这样才能将两个人的能量最大化。
2.2 关于费时问题处理:每个人对某项问题的看法和理解都不一样,在处理费时问题时,两个人各抒己见,解决问题的思路也拓宽了,毕竟一个人的想法还是比较宅,以后再遇到比较难的费时问题时,还需要多跟别人交流,问题会变得简单。
3、给出照片1张,包括结对的2位同学、工作地点、计算机,可选项包括其他能表达结对编程工作经历的物品或场景。
工作地点:冬华B 620寝室
使用本人的电脑进行编程

• 版本控制



