bp算法的一个简单例子

《视觉机器学习20讲》中简单讲解了一下bp算法的基本原理，公式推导看完后不是特别能理解，在网上找到一个不错的例子：BP算法浅谈（Error Back-propagation），对bp算法的理解非常有帮助。于是为了加强记忆，将文中的示例代码用Python重新写了一遍。

 

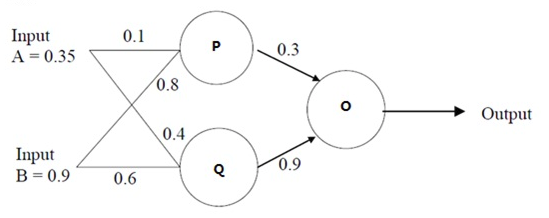
使用梯度下降算法不断迭代更新参数w，使得损失函数（例子中选取平方和误差）最小。参数更新值Δw用链式求导法则求出。

 1 # -*- coding: utf-8 -*-
 2 import numpy as np
 3 def sigmoid(x):#激活函数
 4    return 1/(1+np.exp(-x))
 5 input = np.array([[0.35], [0.9]]) #输入数据
 6 w1 = np.array([[0.1, 0.8], [0.4, 0.6]])#第一层权重参数
 7 w2 = np.array([0.3, 0.9])#第二层权重参数
 8 
 9 real = np.array([[0.5]])#真实值
10 for s in range(0,100,1):
11     pq = sigmoid(np.dot(w1,input))#第一层输出
12     output = sigmoid(np.dot(w2,pq))#第二层输出,也即是最终输出
13     e = output-real #误差
14     if np.square(e)/2<0.01:
15         break
16     else:
17         #否则,按照梯度下降计算权重参数
18         #其中,应用链式法则计算权重参数的更新量
19        w2 = w2 - e*output*(1-output)*pq.T
20        w1 = w1 - e*output*(1-output)*w2*pq.T*(1-pq.T)*input
21 print w1,'\n',w2 #输出最终结果
22 print output

最终结果：

w1: [[ 0.09606536  0.78371966]
 [ 0.38988235  0.55813627]] 

w2: [[ 0.12472196  0.72965595]]

output: [[ 0.63690405]]

 ###

为什么沿着梯度的反方向函数f(x,y)在点P0(x0,y0)处下降得最快？

 ###

梯度下降是求解机器学习算法模型参数的一种常用方法

 

posted @ 2017-12-07 13:59  Lo3King  阅读(6562)  评论(0)  编辑  收藏  举报