人工智能必备数学知识学习笔记16：对称矩阵与矩阵的SVD分解

 

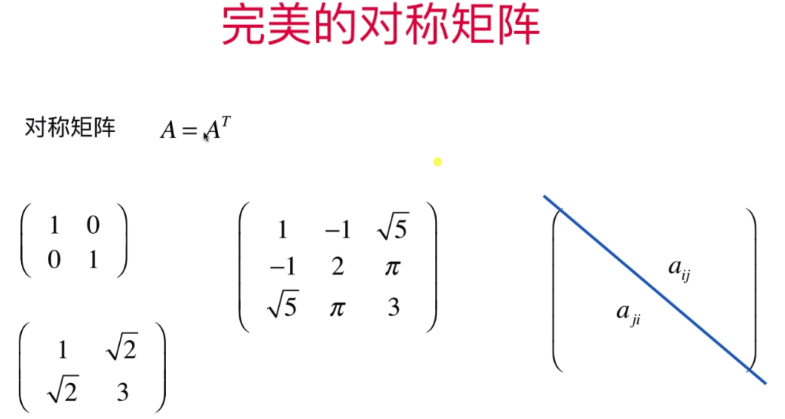
• 完美的对称矩 

   

 

 

 

 

 

 

---

---

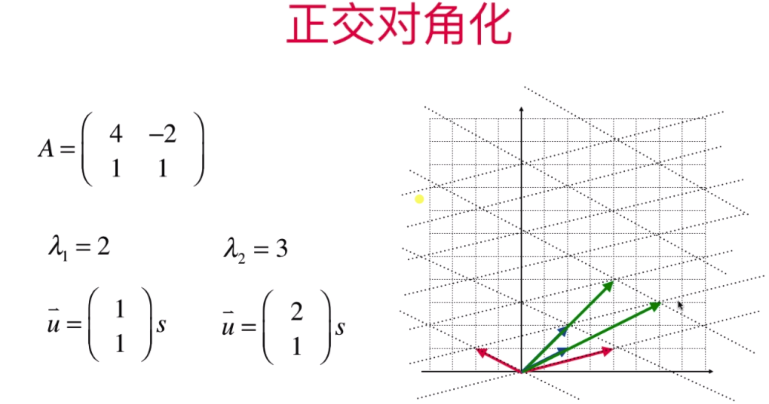
• 正交对角化

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

---

 

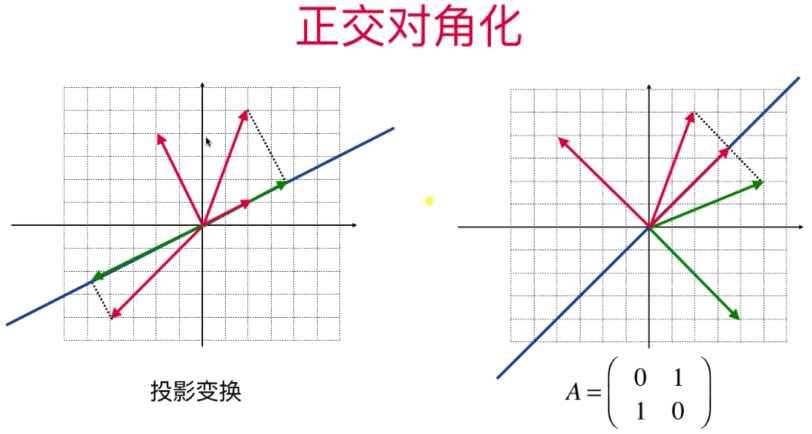
• 什么是奇异值

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

---

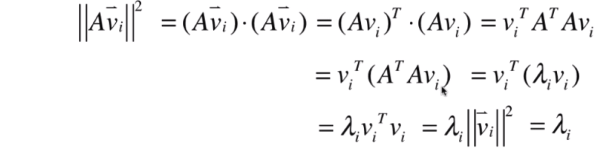
• 奇异值的几何意

   

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

---

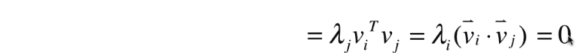
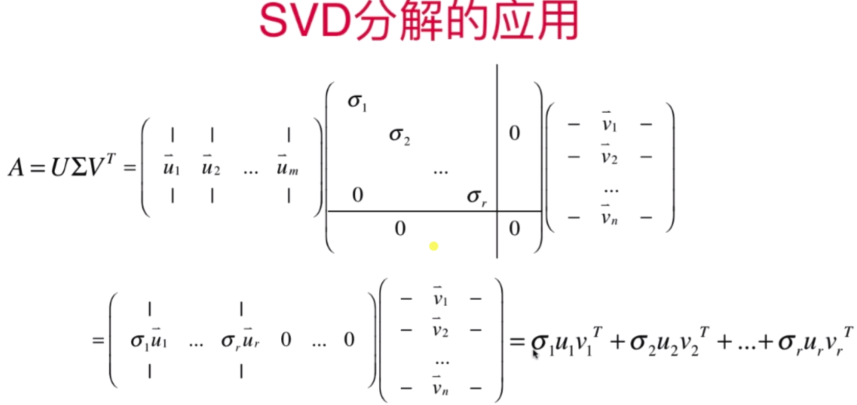
• 矩阵的SVD分解
  

   

 

 

 

 

 

 

 

 

 

 

 

 

 

 

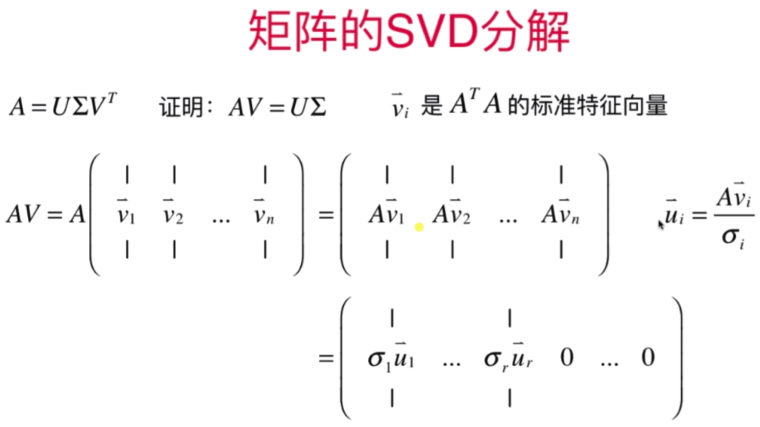
 代码实现：

 

 1.文件 main_svd.py 编写代码：

#矩阵的svd分解
import numpy as np
from scipy.linalg import svd

if __name__ == "__main__":

    A = np.array([[1, 2],
                  [3, 4],
                  [5, 6]])

    U, s, VT = svd(A) #svd分解
    print(U)
    print(s)
    print(VT)
    print()

    Sigma = np.zeros(A.shape)#Sigma矩阵
    for i in range(len(s)):
        Sigma[i][i] = s[i]
    print(Sigma)
    print(U.dot(Sigma).dot(VT))#验证svd（奇异值）分解

2.文件 main_svd.py 运行结果：

/Users/liuxiaoming/PycharmProjects/LinearAlgebra/venv/bin/python /Applications/PyCharm.app/Contents/plugins/python/helpers/pydev/pydevconsole.py --mode=client --port=49318
import sys; print('Python %s on %s' % (sys.version, sys.platform))
sys.path.extend(['/Users/liuxiaoming/PycharmProjects/LinearAlgebra'])
PyDev console: starting.
Python 3.8.2 (v3.8.2:7b3ab5921f, Feb 24 2020, 17:52:18) 
[Clang 6.0 (clang-600.0.57)] on darwin
>>> runfile('/Users/liuxiaoming/PycharmProjects/LinearAlgebra/main_svd.py', wdir='/Users/liuxiaoming/PycharmProjects/LinearAlgebra')
[[-0.2298477   0.88346102  0.40824829]
 [-0.52474482  0.24078249 -0.81649658]
 [-0.81964194 -0.40189603  0.40824829]]
[9.52551809 0.51430058]
[[-0.61962948 -0.78489445]
 [-0.78489445  0.61962948]]
[[9.52551809 0.        ]
 [0.         0.51430058]
 [0.         0.        ]]
[[1. 2.]
 [3. 4.]
 [5. 6.]]
Process finished with exit code 0

---

---

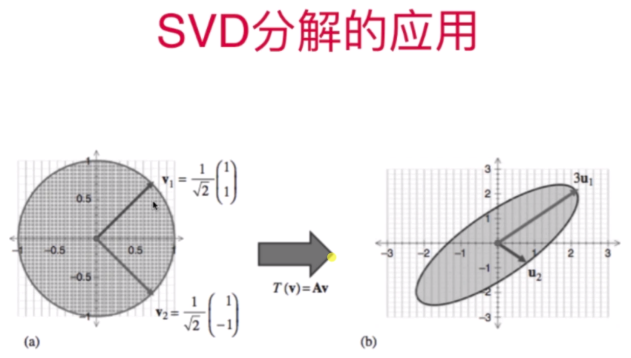
• SVD分解的应用