人工智能必备数学知识学习笔记15:特征值与特征向量

- 什么是特征值和特征向量

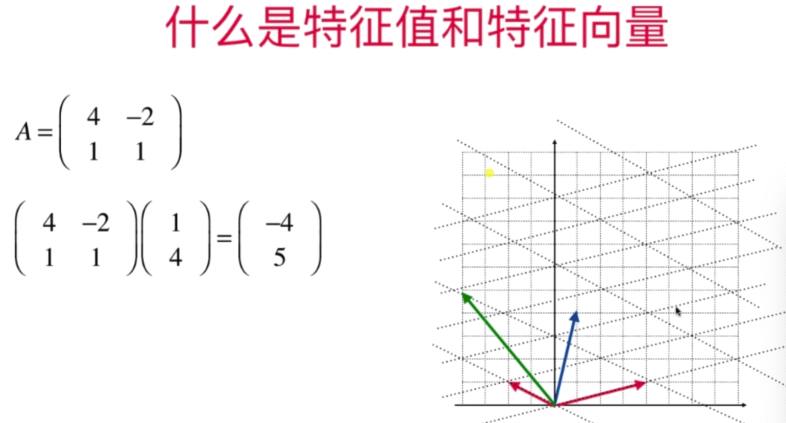
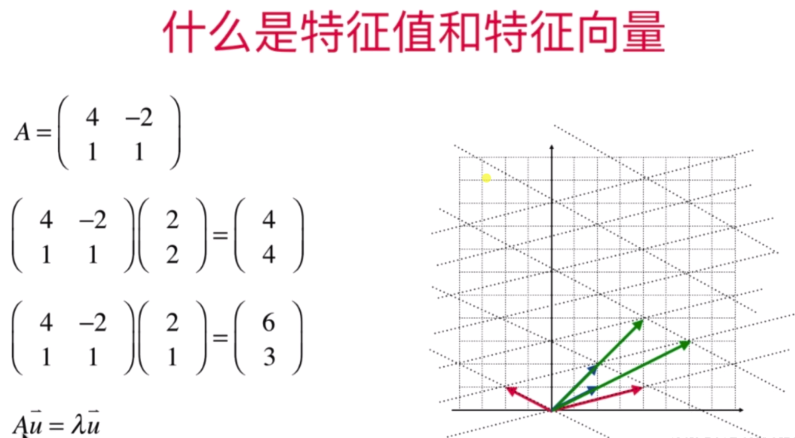
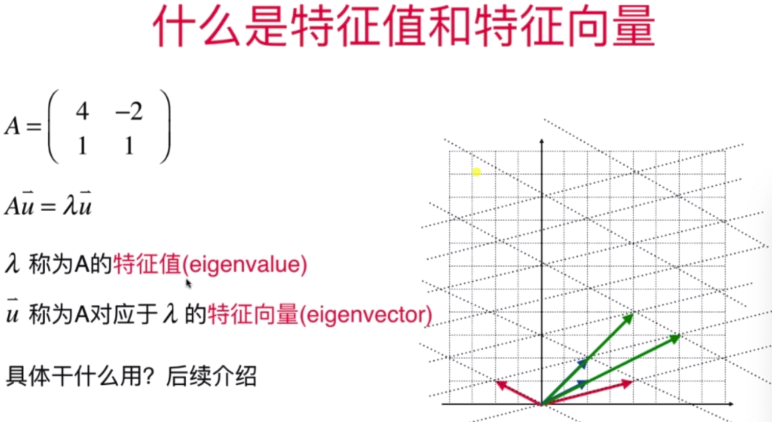




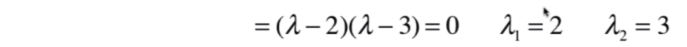


- 特征值和特征向量的相关概






- 特征值与特征向量的性质









直观理解特征值与特征向量

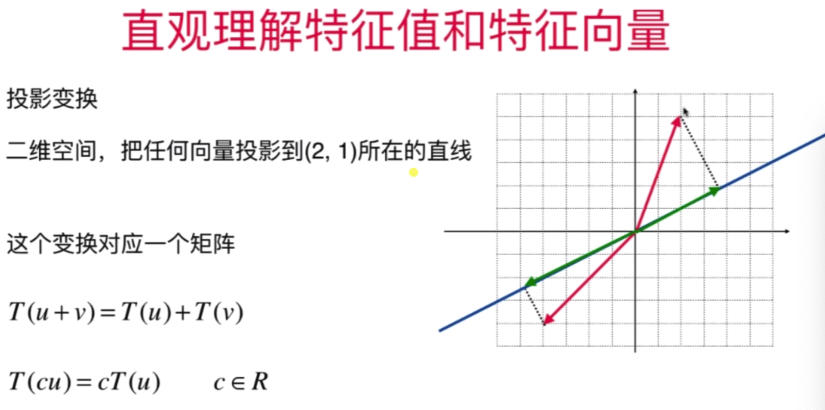
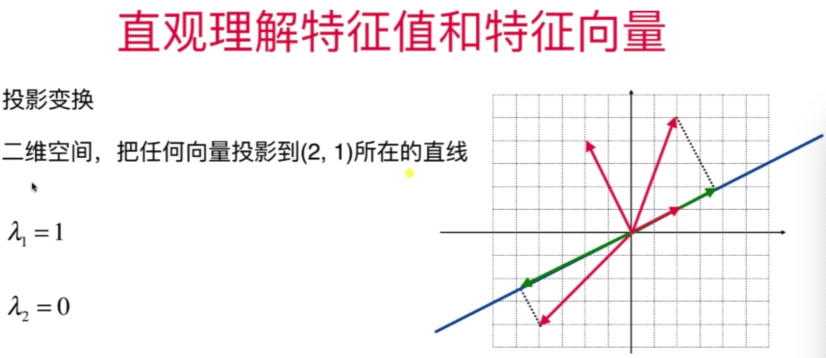
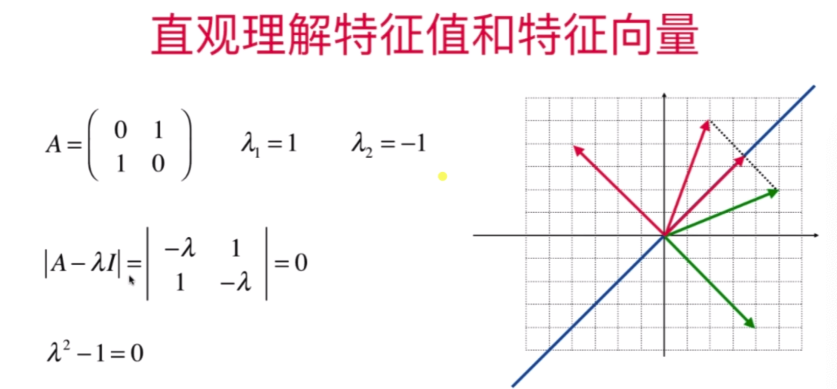

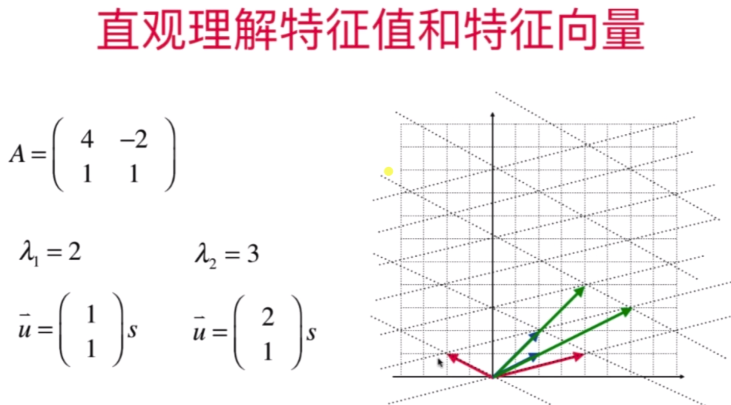

- “不简单”的特征值






代码实现:


1.文件 main_eigen.py 编写代码:
1 #在numpy中求解特征值与特征向量 2 import numpy as np 3 from numpy.linalg import eig 4 5 if __name__ == "__main__": 6 7 A1 = np.array([[4, -2], 8 [1, 1]]); 9 eigenvalues1, eigenvectors1 = eig(A1)#求取矩阵的特征值与特征向量 eigenvalues:特征值 eigenvectors:特征向量 10 print(eigenvalues1) #特征值 11 print(eigenvectors1)#特征向量 12 print() 13 14 # 关于y=x翻转 15 A2 = np.array([[0, 1], 16 [1, 0]]); 17 eigenvalues2, eigenvectors2 = eig(A2)#求取矩阵的特征值与特征向量 eigenvalues:特征值 eigenvectors:特征向量 18 print(eigenvalues2) #特征值 19 print(eigenvectors2)#特征向量 20 print() 21 22 # 旋转90 23 A3 = np.array([[0, -1], 24 [1, 0]]); 25 eigenvalues3, eigenvectors3 = eig(A3)#求取矩阵的特征值与特征向量 eigenvalues:特征值 eigenvectors:特征向量 26 print(eigenvalues3) #特征值 27 print(eigenvectors3)#特征向量 28 print() 29 30 # 单位矩阵 31 A4 = np.array([[1, 0], 32 [0, 1]]); 33 eigenvalues4, eigenvectors4 = eig(A4)#求取矩阵的特征值与特征向量 eigenvalues:特征值 eigenvectors:特征向量 34 print(eigenvalues4) #特征值 35 print(eigenvectors4)#特征向量 36 print() 37 38 # 几何重数为1 39 A5 = np.array([[3, 1], 40 [0, 3]]); 41 eigenvalues5, eigenvectors5 = eig(A5)#求取矩阵的特征值与特征向量 eigenvalues:特征值 eigenvectors:特征向量 42 print(eigenvalues5) #特征值 43 print(eigenvectors5)#特征向量 44 print() 45 46
2.文件 main_eigen.py 运行结果:
1 /Users/liuxiaoming/PycharmProjects/LinearAlgebra/venv/bin/python /Applications/PyCharm.app/Contents/plugins/python/helpers/pydev/pydevconsole.py --mode=client --port=62920 2 import sys; print('Python %s on %s' % (sys.version, sys.platform)) 3 sys.path.extend(['/Users/liuxiaoming/PycharmProjects/LinearAlgebra']) 4 PyDev console: starting. 5 Python 3.8.2 (v3.8.2:7b3ab5921f, Feb 24 2020, 17:52:18) 6 [Clang 6.0 (clang-600.0.57)] on darwin 7 runfile('/Users/liuxiaoming/PycharmProjects/LinearAlgebra/main_eigen.py', wdir='/Users/liuxiaoming/PycharmProjects/LinearAlgebra') 8 [3. 2.] 9 [[0.89442719 0.70710678] 10 [0.4472136 0.70710678]] 11 [ 1. -1.] 12 [[ 0.70710678 -0.70710678] 13 [ 0.70710678 0.70710678]] 14 [0.+1.j 0.-1.j] 15 [[0.70710678+0.j 0.70710678-0.j ] 16 [0. -0.70710678j 0. +0.70710678j]] 17 [1. 1.] 18 [[1. 0.] 19 [0. 1.]] 20 [3. 3.] 21 [[ 1.00000000e+00 -1.00000000e+00] 22 [ 0.00000000e+00 6.66133815e-16]]
- 矩阵相似和背后的重要含义

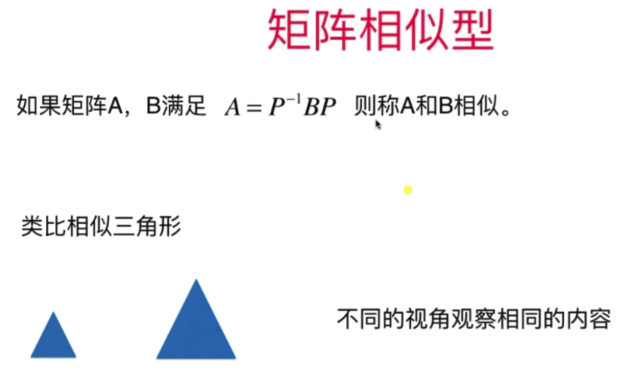

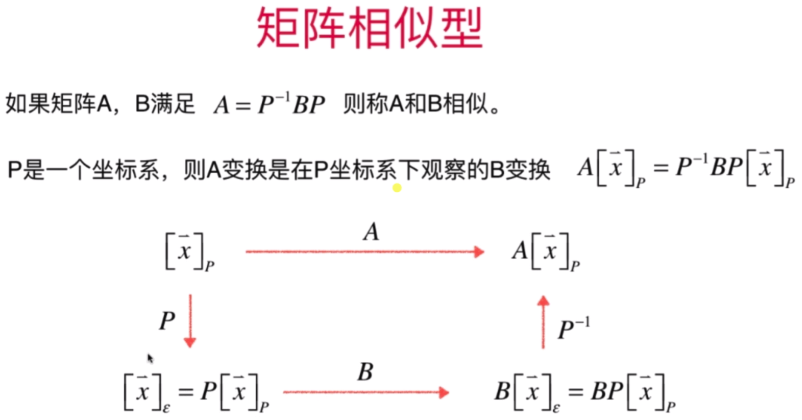


- 矩阵对角






代码实现:

1.调用文件 Matrix.py :
1 #矩阵类 2 from playLA.Vector import Vector 3 4 5 class Matrix: 6 # 参数2:二维数组 7 def __init__(self, list2d): 8 if isinstance(list2d[0], list): #若二维数组为 list 集合 9 self._values = [row[:] for row in list2d] # 将数组变为矩阵 10 elif isinstance(list2d[0], Vector): #若二维数组 为向量时 11 self._values = [row.underlying_list() for row in list2d] #将数组中的每一行作为一个数组放到一个大的数组中 12 13 #矩阵类方法:返回一个r行c列的零矩阵:参数1:为零的类对象 14 @classmethod 15 def zero(cls,r,c): 16 return cls([[0] * c for _ in range(r)]) #创建一个r行c列为零的一个列表 17 18 #单位矩阵类方法:返回一个n行n列的单位矩阵 19 @classmethod 20 def identity(cls, n): 21 m = [[0] * n for _ in range(n)] #此处 m 代表有 n 行,每一行有 n 个 0 22 for i in range(n): 23 m[i][i] = 1 #此处代表将矩阵 m 的 第i行的第i个元素赋值为1 24 return cls(m) 25 26 #返回矩阵的转置矩阵 27 def T(self): 28 #将每一行的相同位置(每一列)元素提取出来变为行组成新的矩阵 29 return Matrix([[e for e in self.col_vector(i)] 30 for i in range(self.col_num())]) 31 32 #返回两个矩阵的加法结果 33 def __add__(self, another): 34 # 校验两个矩阵的形状为一致(行数、列数一致) 35 assert self.shape() == another.shape(), \ 36 "Error in adding. Shape of matrix must be same." 37 # 根据矩阵的加法公式:两个矩阵对应的每一行的每一个元素相加,获得新的矩阵(遍历两个矩阵对应的每一个行每个元素进行相加<第二步>,外部再遍历该矩阵的行数(循环的次数)<第一步>) 38 return Matrix([[a+b for a,b in zip(self.row_vector(i),another.row_vector(i))] 39 for i in range(self.row_num())]) 40 41 # 返回两个矩阵的减法结果 42 def __sub__(self, another): 43 assert self.shape() == another.shape(), \ 44 "Error in subtracting. Shape of matrix must be same." 45 return Matrix([[a - b for a, b in zip(self.row_vector(i), another.row_vector(i))] 46 for i in range(self.row_num())]) 47 48 #返回两个矩阵的乘法结果(矩阵乘以矩阵) 49 def dot(self,another): 50 if isinstance(another,Vector):#判断是否为向量:矩阵与向量的乘法 51 assert self.col_num() == len(another),\ 52 "Error in Matrix_Vector Multiplication." #矩阵与向量的乘法错误 53 return Vector([self.row_vector(i).dot(another) for i in range(self.row_num())]) 54 if isinstance(another,Matrix):#判断是否为矩阵:矩阵与矩阵的乘法 55 assert self.col_num() == another.row_num(),\ 56 "Error in Matrix-Matrix Multiplication." #矩阵与矩阵的乘法错误 57 # 将矩阵的每一行与另一矩阵的每一列进行向量间的点乘 58 return Matrix([[self.row_vector(i).dot(another.col_vector(j)) for j in range(another.col_num())] 59 for i in range(self.row_num())]) 60 61 #返回矩阵的数量乘结果(矩阵乘以数字):self * k 62 def __mul__(self, k): 63 #通过遍历每一行的每个元素e后分别乘以k<第一步>,外部再遍历该矩阵的行数(循环的次数)<第二步> 64 return Matrix([[e * k for e in self.row_vector(i)] 65 for i in range(self.row_num())]) 66 67 # 返回矩阵的数量乘结果(数字乘以矩阵):k * self 68 def __rmul__(self, k): 69 return self * k 70 71 #返回数量除法的结果矩阵:self / k 72 def __truediv__(self, k): 73 return (1 / k) * self 74 75 #返回矩阵取正的结果 76 def __pos__(self): 77 return 1 * self 78 79 #返回矩阵取负的结果 80 def __neg__(self): 81 return -1 * self 82 83 #返回矩阵的第index个行向量 84 def row_vector(self,index): 85 return Vector(self._values[index]) 86 87 # 返回矩阵的第index个列向量 88 def col_vector(self, index): 89 return Vector([row[index] for row in self._values]) 90 91 #返回矩阵pos位置的元素(根据元素的位置取元素值) :参数2:元组 92 def __getitem__(self, pos): 93 r,c = pos 94 return self._values[r][c] 95 96 #返回矩阵的元素个数 97 def size(self): 98 r,c = self.shape() 99 return r*c 100 101 #返回矩阵行数 102 def row_num(self): 103 return self.shape()[0] 104 105 __len__ = row_num 106 107 #返回矩阵列数 108 def col_num(self): 109 return self.shape()[1] 110 111 #返回矩阵形状:(行数,列数) 112 def shape(self): 113 return len(self._values),len(self._values[0]) 114 115 #矩阵展示 116 def __repr__(self): 117 return "Matrix({})".format(self._values) 118 119 __str__ = __repr__
2.调用文件 LinearSystem.py :
1 from playLA.Matrix import Matrix 2 from playLA.Vector import Vector 3 from playLA._global import is_zero 4 5 6 #线性系统 7 class LinearSystem: 8 9 #初始化函数:参数A:增广矩阵的等号左边的系数 参数b:增广矩阵的等号右边的值(方程右边的结果) 10 def __init__(self, A, b): 11 #判断 b为None 或者 矩阵A的行数等于b的列数 12 assert b is None or A.row_num() == len(b),\ 13 "row number of A must be equal to the length of b" 14 self._m = A.row_num()#行数 15 self._n = A.col_num()#列数 16 17 #判断若b为空时,则该矩阵为A矩阵 TODO:2020-08-22 18 if b is None: 19 self.Ab = [A.row_vector(i) for i in range(self._m)] 20 21 if isinstance(b, Vector):#如果等号右侧方程结果为列向量时 22 #增广矩阵 23 self.Ab = [Vector(A.row_vector(i).underlying_list() + [b[i]]) 24 for i in range(self._m)] 25 26 if isinstance(b, Matrix):#如果等号右侧方程结果为单位矩阵时 27 #增广矩阵 28 self.Ab = [Vector(A.row_vector(i).underlying_list() + b.row_vector(i).underlying_list()) 29 for i in range(self._m)] 30 #主元 31 self.pivots = [] 32 33 #寻找最大主源系数 34 def _max_row(self, index_i, index_j, n): 35 best, ret = self.Ab[index_i][index_j], index_i #存储第index行index列的元素值与当前index的值 36 for i in range(index_i + 1, n): #从index+1开始一直遍历到n 37 if self.Ab[i][index_j] > best: 38 best, ret = self.Ab[i][index_j], i 39 return ret 40 41 #高斯—约旦消元法-前向过程 42 def _forward(self): 43 44 i,k = 0,0 45 while i < self._m and k < self._n: 46 #看Ab[i][k]位置是否为主元 47 max_row = self._max_row(i, k, self._m)#寻找最大主源系数的行数 48 self.Ab[i], self.Ab[max_row] = self.Ab[max_row],self.Ab[i] #行交换操作 49 50 if is_zero(self.Ab[i][k]):#判断此时该值是否为0 51 k += 1 52 else: 53 #将主元归为一 54 self.Ab[i] = self.Ab[i] / self.Ab[i][k] 55 #将当前主源下的所有行对应主源列的元素全部归为0 :也就是第一次循环会将该主源下的所有对应列变为0,第二次循环会将第二次主源列下的所有对应列变为0 56 for j in range(i + 1, self._m): 57 self.Ab[j] =self.Ab[j] -self.Ab[j][k] * self.Ab[i]#该主源行下的所有行减去主源行 58 self.pivots.append(k) 59 i += 1 60 61 #高斯-约旦消元法-后向过程 62 def _backward(self): 63 n = len(self.pivots) 64 #n = self._m #行数 65 for i in range(n-1, -1, -1): #反向遍历且 从参数1的位置遍历到参数2的位置,也就是从倒数第一个位置遍历到第一个位置,参数3为步长(遍历的方向及单位) 66 k = self.pivots[i] 67 #Ab[i][k]为主源 68 for j in range(i-1, -1, -1): 69 self.Ab[j] = self.Ab[j] - self.Ab[j][k] * self.Ab[i]#该主源行上的所有行减去主源行 70 71 #高斯-约旦消元法:如果有解,返回True;如果没有解,返回False 72 def gauss_jordan_elimination(self): 73 # 高斯—约旦消元法-前向过程 74 self._forward() 75 # 高斯-约旦消元法-后向过程 76 self._backward() 77 for i in range(len(self.pivots), self._m):#此处为最后一行的非零行下一行的全零行的结果值不为零的判断 0.0 0.0 | 5.0 78 if not is_zero(self.Ab[i][-1]): 79 return False 80 return True 81 82 # 打印结果(求每个未知数的值) 83 def fancy_print(self): 84 for i in range(self._m): 85 print(" ".join(str(self.Ab[i][j]) for j in range(self._n)),end=" ") 86 print("|",self.Ab[i][-1]) 87 88 89 #求增广矩阵的逆 90 def inv(A): 91 92 if A.row_num() != A.col_num():#判断矩阵行是否等于列,若不等于无解 93 return None 94 95 n = A.row_num() # TODO:A.row_num 无括号代表方法,类型为method A.row_num() 有括号代表具体的返回值 96 print(n,type(n)) 97 ls = LinearSystem(A, Matrix.identity(n))#实例化一个线性系统(创建一个增广矩阵) 98 if not ls.gauss_jordan_elimination(): #判断是否有逆矩阵(是否有解) 99 return None 100 101 invA = [[row[i] for i in range(n, n*n)] for row in ls.Ab] #将右侧的单位矩阵拼接到矩阵中 102 103 return Matrix(invA) 104 105 106 #求矩阵的秩(主元数量) 107 def rank(A): 108 109 ls = LinearSystem(A,None) #声明一个矩阵A 110 ls.gauss_jordan_elimination() #将矩阵进行高斯消元 111 112 zero = Vector.zero(A.col_num()) #创建零向量(维度为该矩阵的列数即可,每一行的元素个数) 113 return sum([row != zero for row in ls.Ab]) #判断有多少非零行 (不等指的是向量间是否不等)
3.文件 main_diag.py 编写代码:
1 import numpy as np 2 from numpy.linalg import eig, inv # eig:特征值、特征向量 inv:矩阵的逆 3 from playLA.LinearSystem import rank # 矩阵的秩(主元数量) 4 from playLA.Matrix import Matrix 5 6 #矩阵的对角化 7 def diagonalize(A): 8 9 assert A.ndim == 2 #判断A的维度为2 10 assert A.shape[0] == A.shape[1] #判断矩阵A的长等于宽(是否为方阵) 11 12 eigenvalues, eigenvectors = eig(A)#求取矩阵的特征值与特征向量 13 14 P = eigenvectors #特征向量 15 if rank(Matrix(P.tolist())) != A.shape[0]:# 判断矩阵是否满秩(满秩矩阵可逆,不满秩则矩阵不可逆) 16 print("Matrix can not be diagonalized")#矩阵不能对角化 17 return None, None, None 18 19 D = np.diag(eigenvalues) #将特征值放入矩阵的对角线上 20 Pinv = inv(P) #特征向量的逆 21 22 23 return P, D, Pinv 24 25 26 if __name__ == "__main__": 27 28 A1 = np.array([[4, -2], 29 [1, 1]]) 30 P1, D1, Pinv1 = diagonalize(A1) 31 print(P1) 32 print(D1) 33 print(Pinv1) 34 print(P1.dot(D1).dot(Pinv1)) 35 36 A2 = np.array([[3, 1], 37 [0, 3]]) 38 P2, D2, Pinv2 = diagonalize(A2) 39 print(P2) 40 print(D2) 41 print(Pinv2)
4.文件 main_diag.py 运行结果:
1 /Users/liuxiaoming/PycharmProjects/LinearAlgebra/venv/bin/python /Applications/PyCharm.app/Contents/plugins/python/helpers/pydev/pydevconsole.py --mode=client --port=63553 2 import sys; print('Python %s on %s' % (sys.version, sys.platform)) 3 sys.path.extend(['/Users/liuxiaoming/PycharmProjects/LinearAlgebra']) 4 PyDev console: starting. 5 Python 3.8.2 (v3.8.2:7b3ab5921f, Feb 24 2020, 17:52:18) 6 [Clang 6.0 (clang-600.0.57)] on darwin 7 runfile('/Users/liuxiaoming/PycharmProjects/LinearAlgebra/main_diag.py', wdir='/Users/liuxiaoming/PycharmProjects/LinearAlgebra') 8 [[0.89442719 0.70710678] 9 [0.4472136 0.70710678]] 10 [[3. 0.] 11 [0. 2.]] 12 [[ 2.23606798 -2.23606798] 13 [-1.41421356 2.82842712]] 14 [[ 4. -2.] 15 [ 1. 1.]] 16 Matrix can not be diagonalized 17 None 18 None 19 None
- 矩阵对角化的应用:求解矩阵的幂和动态系统










