人工智能必备数学知识学习笔记12:正交性,标准正交矩阵和投影
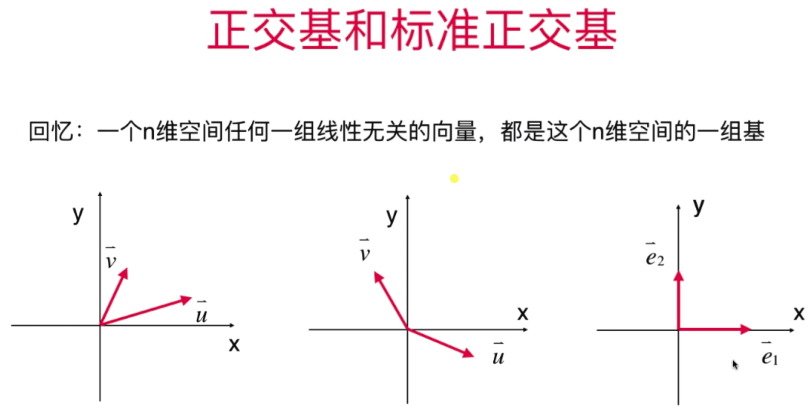
- 正交基和标准正交基







- 一维投影


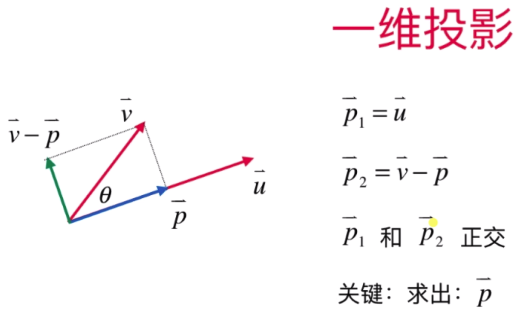
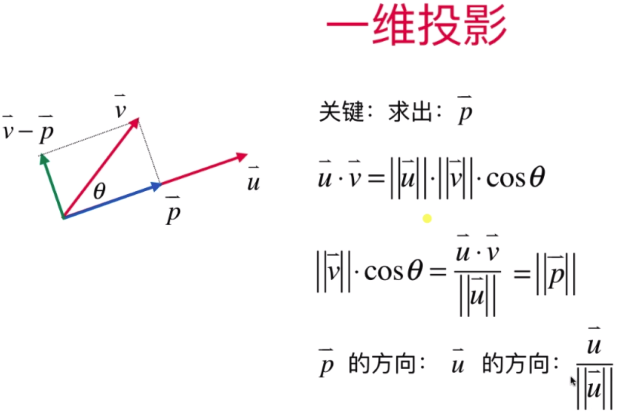
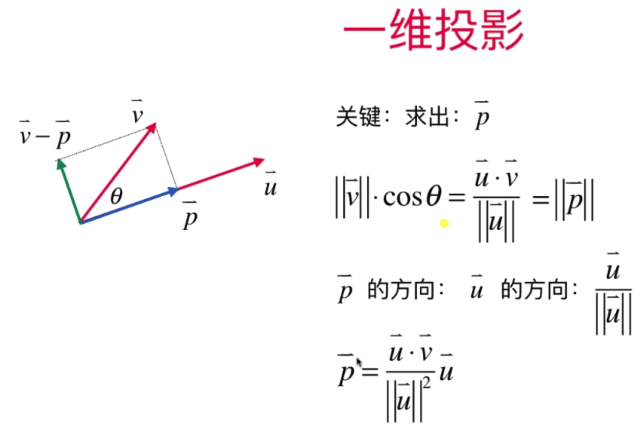
求出向量P的思路:先根据余弦定理求出向量p,再求出向量P的单位向量,再通过单位向量乘以向量P的模,就得出向量P
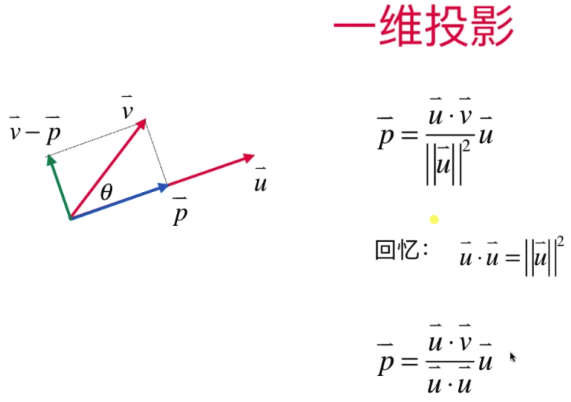
注: 分数线上下 向量U无法约掉
- 高维投影和Gram-Schmidt过程



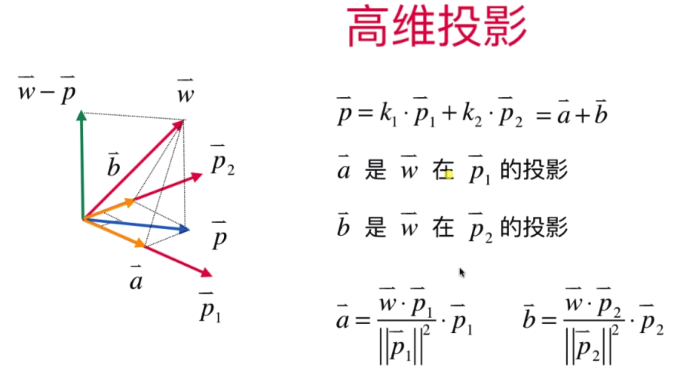
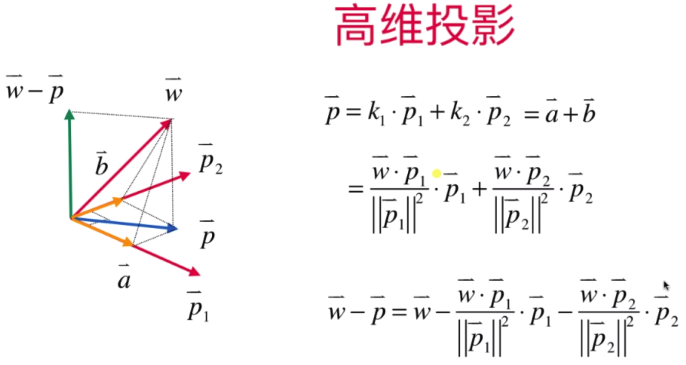
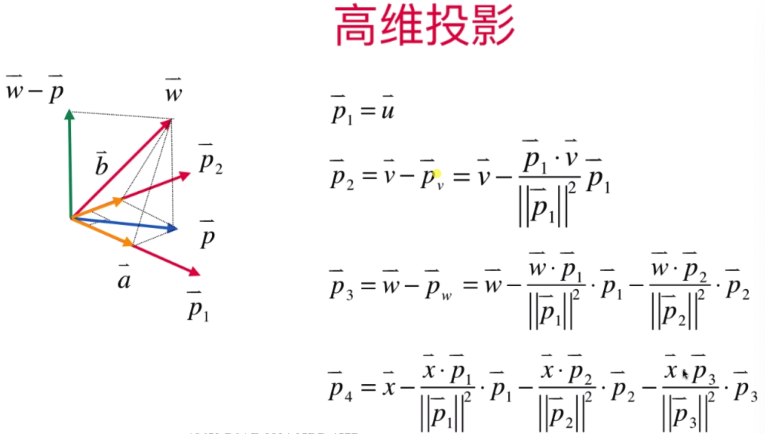
高维投影:如三维投影需要将向量W 在向量P1、P2所组成的面上 做一个垂线




代码实现:
1.在文件 Matrix.py 编写代码:在__init__方法中增加判断条件:若二维数组 为向量时
1 #矩阵类 2 from playLA.Vector import Vector 3 4 5 class Matrix: 6 # 参数2:二维数组 7 def __init__(self, list2d): 8 if isinstance(list2d[0], list): #若二维数组为 list 集合 9 self._values = [row[:] for row in list2d] # 将数组变为矩阵 10 elif isinstance(list2d[0], Vector): #若二维数组 为向量时 11 self._values = [row.underlying_list() for row in list2d] #将数组中的每一行作为一个数组放到一个大的数组中 12 13 #矩阵类方法:返回一个r行c列的零矩阵:参数1:为零的类对象 14 @classmethod 15 def zero(cls,r,c): 16 return cls([[0] * c for _ in range(r)]) #创建一个r行c列为零的一个列表 17 18 #单位矩阵类方法:返回一个n行n列的单位矩阵 19 @classmethod 20 def identity(cls, n): 21 m = [[0] * n for _ in range(n)] #此处 m 代表有 n 行,每一行有 n 个 0 22 for i in range(n): 23 m[i][i] = 1 #此处代表将矩阵 m 的 第i行的第i个元素赋值为1 24 return cls(m) 25 26 #返回矩阵的转置矩阵 27 def T(self): 28 #将每一行的相同位置(每一列)元素提取出来变为行组成新的矩阵 29 return Matrix([[e for e in self.col_vector(i)] 30 for i in range(self.col_num())]) 31 32 #返回两个矩阵的加法结果 33 def __add__(self, another): 34 # 校验两个矩阵的形状为一致(行数、列数一致) 35 assert self.shape() == another.shape(), \ 36 "Error in adding. Shape of matrix must be same." 37 # 根据矩阵的加法公式:两个矩阵对应的每一行的每一个元素相加,获得新的矩阵(遍历两个矩阵对应的每一个行每个元素进行相加<第二步>,外部再遍历该矩阵的行数(循环的次数)<第一步>) 38 return Matrix([[a+b for a,b in zip(self.row_vector(i),another.row_vector(i))] 39 for i in range(self.row_num())]) 40 41 # 返回两个矩阵的减法结果 42 def __sub__(self, another): 43 assert self.shape() == another.shape(), \ 44 "Error in subtracting. Shape of matrix must be same." 45 return Matrix([[a - b for a, b in zip(self.row_vector(i), another.row_vector(i))] 46 for i in range(self.row_num())]) 47 48 #返回两个矩阵的乘法结果(矩阵乘以矩阵) 49 def dot(self,another): 50 if isinstance(another,Vector):#判断是否为向量:矩阵与向量的乘法 51 assert self.col_num() == len(another),\ 52 "Error in Matrix_Vector Multiplication." #矩阵与向量的乘法错误 53 return Vector([self.row_vector(i).dot(another) for i in range(self.row_num())]) 54 if isinstance(another,Matrix):#判断是否为矩阵:矩阵与矩阵的乘法 55 assert self.col_num() == another.row_num(),\ 56 "Error in Matrix-Matrix Multiplication." #矩阵与矩阵的乘法错误 57 # 将矩阵的每一行与另一矩阵的每一列进行向量间的点乘 58 return Matrix([[self.row_vector(i).dot(another.col_vector(j)) for j in range(another.col_num())] 59 for i in range(self.row_num())]) 60 61 #返回矩阵的数量乘结果(矩阵乘以数字):self * k 62 def __mul__(self, k): 63 #通过遍历每一行的每个元素e后分别乘以k<第一步>,外部再遍历该矩阵的行数(循环的次数)<第二步> 64 return Matrix([[e * k for e in self.row_vector(i)] 65 for i in range(self.row_num())]) 66 67 # 返回矩阵的数量乘结果(数字乘以矩阵):k * self 68 def __rmul__(self, k): 69 return self * k 70 71 #返回数量除法的结果矩阵:self / k 72 def __truediv__(self, k): 73 return (1 / k) * self 74 75 #返回矩阵取正的结果 76 def __pos__(self): 77 return 1 * self 78 79 #返回矩阵取负的结果 80 def __neg__(self): 81 return -1 * self 82 83 #返回矩阵的第index个行向量 84 def row_vector(self,index): 85 return Vector(self._values[index]) 86 87 # 返回矩阵的第index个列向量 88 def col_vector(self, index): 89 return Vector([row[index] for row in self._values]) 90 91 #返回矩阵pos位置的元素(根据元素的位置取元素值) :参数2:元组 92 def __getitem__(self, pos): 93 r,c = pos 94 return self._values[r][c] 95 96 #返回矩阵的元素个数 97 def size(self): 98 r,c = self.shape() 99 return r*c 100 101 #返回矩阵行数 102 def row_num(self): 103 return self.shape()[0] 104 105 __len__ = row_num 106 107 #返回矩阵列数 108 def col_num(self): 109 return self.shape()[1] 110 111 #返回矩阵形状:(行数,列数) 112 def shape(self): 113 return len(self._values),len(self._values[0]) 114 115 #矩阵展示 116 def __repr__(self): 117 return "Matrix({})".format(self._values) 118 119 __str__ = __repr__
2.在文件 GramSchmidtProcess.py 编写代码:
1 from .Vector import Vector 2 from .Matrix import Matrix 3 from .LinearSystem import rank 4 5 6 #格拉姆-斯密特过程(参数为一组基-各个向量) 7 def gram_schmidt_process(basis): 8 #矩阵的秩 9 matrix = Matrix(basis)#初始化为矩阵 10 assert rank(matrix) == len(basis) #矩阵的秩 与这组基是否相等 11 12 #根据 #格拉姆-斯密特 公式分别计算向量P1、P2...再放入集合中 13 res = [basis[0]] 14 for i in range(1, len(basis)): 15 p = basis[i] 16 for r in res: 17 p = p - basis[i].dot(r) / r.dot(r) * r 18 res.append(p) 19 return res
3.在文件 main_garm_schmidt_process.py 编写代码:
1 from playLA.Vector import Vector 2 from playLA.GramSchmidtProcess import gram_schmidt_process 3 4 if __name__ == "__main__": 5 6 #根据 格拉姆-斯密特过程 求出该空间基的正交基 7 basis1 = [Vector([2, 1]), Vector([1, 1])] #空间的基 8 res1 = gram_schmidt_process(basis1) #根据 格拉姆-斯密特过程 求出该空间基的正交基 9 for row in res1: 10 print("正交基 = {}".format(row)) 11 12 #根据得出的正交基得出 13 res1 = [row / row.norm() for row in res1] 14 for row in res1: 15 print("标准正交基 = {}".format(row)) 16 #验证是否为正交基(判断各个向量是否垂直的条件为:两个向量点乘为0) 17 print(res1[0].dot(res1[1])) 18 print("-"*50) 19 20 #----------------------------------------------------------------------- 21 22 #根据 格拉姆-斯密特过程 求出该空间基的正交基 23 basis2 = [Vector([2, 3]), Vector([4, 5])] #空间的基 24 res2 = gram_schmidt_process(basis2) #根据 格拉姆-斯密特过程 求出该空间基的正交基 25 for row in res2: 26 print("正交基 = {}".format(row)) 27 28 #根据得出的正交基得出 29 res2 = [row / row.norm() for row in res2] 30 for row in res2: 31 print("标准正交基 = {}".format(row)) 32 #验证是否为正交基(判断各个向量是否垂直的条件为:两个向量点乘为0) 33 print(res2[0].dot(res2[1])) 34 print("-" * 50) 35 36 #三维向量----------------------------------------------------------------------- 37 38 #根据 格拉姆-斯密特过程 求出该空间基的正交基 39 basis3 = [Vector([1, 0, 1]), Vector([3, 1, 1]), Vector([-1, -1, -1])] #空间的基 40 res3 = gram_schmidt_process(basis3) #根据 格拉姆-斯密特过程 求出该空间基的正交基 41 for row in res3: 42 print("正交基 = {}".format(row)) 43 44 #根据得出的正交基得出 45 res3 = [row / row.norm() for row in res3] 46 for row in res3: 47 print("标准正交基 = {}".format(row)) 48 #验证是否为正交基(判断各个向量是否垂直的条件为:两个向量点乘为0) 49 print(res3[0].dot(res3[1])) 50 print("-" * 50) 51 52 #三个四维向量----------------------------------------------------------------------- 53 54 #根据 格拉姆-斯密特过程 求出该空间基的正交基 55 basis3 = [Vector([1, 1, 5, 2]), Vector([-3, 3, 4, -2]), Vector([-1, -2, 2, 5])] #空间的基 56 res3 = gram_schmidt_process(basis3) #根据 格拉姆-斯密特过程 求出该空间基的正交基 57 for row in res3: 58 print("正交基 = {}".format(row)) 59 60 #根据得出的正交基得出 61 res3 = [row / row.norm() for row in res3] 62 for row in res3: 63 print("标准正交基 = {}".format(row)) 64 #验证是否为正交基(判断各个向量是否垂直的条件为:两个向量点乘为0) 65 print(res3[0].dot(res3[1])) 66 print("-" * 50)
4. 文件 main_garm_schmidt_process.py 运行结果为:
1 /Users/liuxiaoming/PycharmProjects/LinearAlgebra/venv/bin/python /Applications/PyCharm.app/Contents/plugins/python/helpers/pydev/pydevconsole.py --mode=client --port=51095 2 import sys; print('Python %s on %s' % (sys.version, sys.platform)) 3 sys.path.extend(['/Users/liuxiaoming/PycharmProjects/LinearAlgebra']) 4 PyDev console: starting. 5 Python 3.8.2 (v3.8.2:7b3ab5921f, Feb 24 2020, 17:52:18) 6 [Clang 6.0 (clang-600.0.57)] on darwin 7 runfile('/Users/liuxiaoming/PycharmProjects/LinearAlgebra/main_garm_schmidt_process.py', wdir='/Users/liuxiaoming/PycharmProjects/LinearAlgebra') 8 正交基 = (2, 1) 9 正交基 = (-0.19999999999999996, 0.4) 10 标准正交基 = (0.8944271909999159, 0.4472135954999579) 11 标准正交基 = (-0.44721359549995787, 0.894427190999916) 12 1.1102230246251565e-16 13 -------------------------------------------------- 14 正交基 = (2, 3) 15 正交基 = (0.4615384615384617, -0.3076923076923075) 16 标准正交基 = (0.5547001962252291, 0.8320502943378437) 17 标准正交基 = (0.8320502943378439, -0.5547001962252287) 18 4.996003610813204e-16 19 -------------------------------------------------- 20 正交基 = (1, 0, 1) 21 正交基 = (1.0, 1.0, -1.0) 22 正交基 = (0.3333333333333333, -0.6666666666666667, -0.3333333333333333) 23 标准正交基 = (0.7071067811865475, 0.0, 0.7071067811865475) 24 标准正交基 = (0.5773502691896258, 0.5773502691896258, -0.5773502691896258) 25 标准正交基 = (0.40824829046386296, -0.816496580927726, -0.40824829046386296) 26 0.0 27 -------------------------------------------------- 28 正交基 = (1, 1, 5, 2) 29 正交基 = (-3.5161290322580645, 2.4838709677419355, 1.4193548387096775, -3.032258064516129) 30 正交基 = (-3.176789587852494, -1.3980477223427332, -0.08459869848156165, 2.4989154013015185) 31 标准正交基 = (0.1796053020267749, 0.1796053020267749, 0.8980265101338746, 0.3592106040535498) 32 标准正交基 = (-0.6447334317039531, 0.4554538921211412, 0.2602593669263664, -0.5560086475245101) 33 标准正交基 = (-0.7426488253165523, -0.32682633521100585, -0.019776923309897908, 0.584179888538524) 34 2.7755575615628914e-17 35 --------------------------------------------------
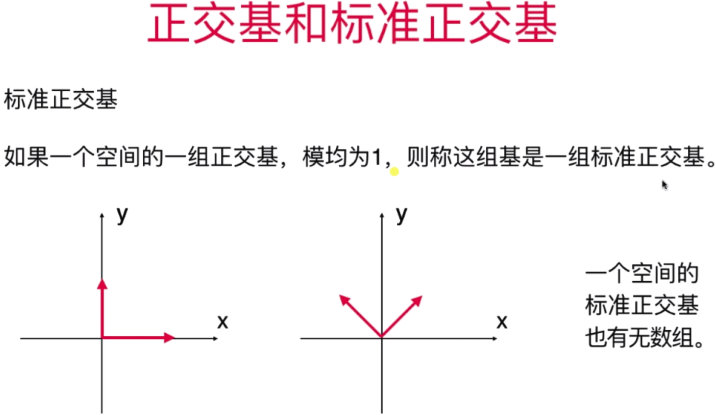
- 标准正交基的性质

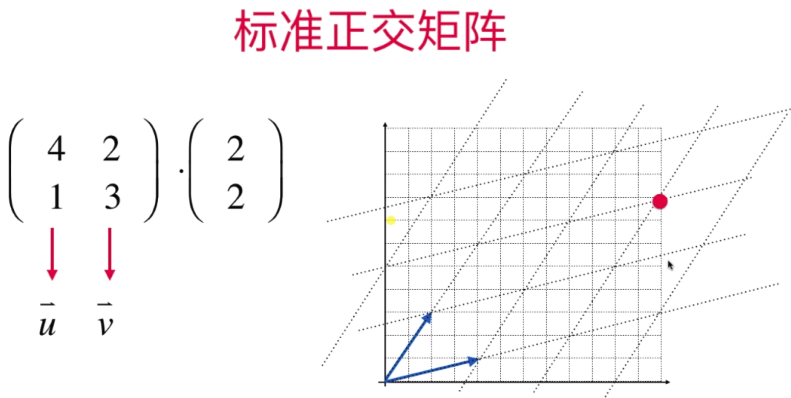


其中 模的平方是1,其他向量相乘为0,所以该矩阵主元行程的对角线上的元素均为1,其他元素均为0,得证,该矩阵为单位矩阵



- 矩阵的QR分解

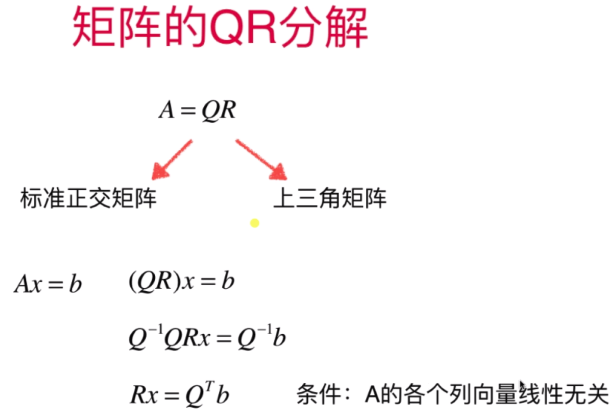

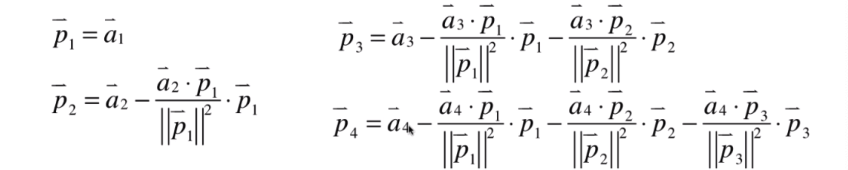





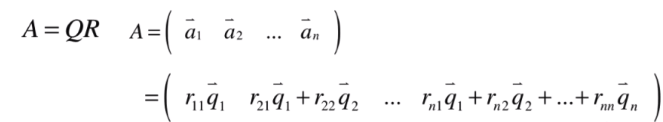
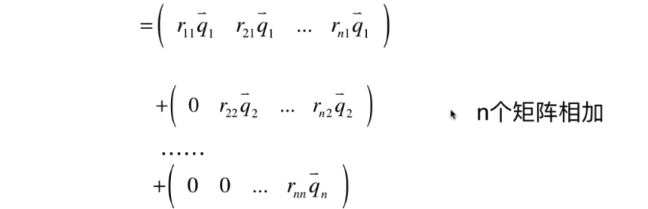
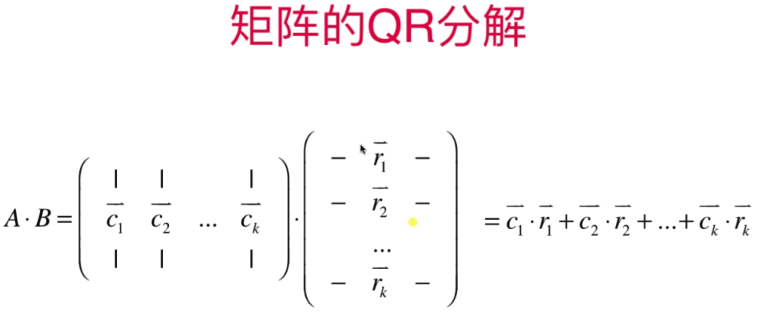


代码实现:
1.文件Matrix.py调用:
1 #矩阵类 2 from playLA.Vector import Vector 3 4 5 class Matrix: 6 # 参数2:二维数组 7 def __init__(self, list2d): 8 if isinstance(list2d[0], list): #若二维数组为 list 集合 9 self._values = [row[:] for row in list2d] # 将数组变为矩阵 10 elif isinstance(list2d[0], Vector): #若二维数组 为向量时 11 self._values = [row.underlying_list() for row in list2d] #将数组中的每一行作为一个数组放到一个大的数组中 12 13 #矩阵类方法:返回一个r行c列的零矩阵:参数1:为零的类对象 14 @classmethod 15 def zero(cls,r,c): 16 return cls([[0] * c for _ in range(r)]) #创建一个r行c列为零的一个列表 17 18 #单位矩阵类方法:返回一个n行n列的单位矩阵 19 @classmethod 20 def identity(cls, n): 21 m = [[0] * n for _ in range(n)] #此处 m 代表有 n 行,每一行有 n 个 0 22 for i in range(n): 23 m[i][i] = 1 #此处代表将矩阵 m 的 第i行的第i个元素赋值为1 24 return cls(m) 25 26 #返回矩阵的转置矩阵 27 def T(self): 28 #将每一行的相同位置(每一列)元素提取出来变为行组成新的矩阵 29 return Matrix([[e for e in self.col_vector(i)] 30 for i in range(self.col_num())]) 31 32 #返回两个矩阵的加法结果 33 def __add__(self, another): 34 # 校验两个矩阵的形状为一致(行数、列数一致) 35 assert self.shape() == another.shape(), \ 36 "Error in adding. Shape of matrix must be same." 37 # 根据矩阵的加法公式:两个矩阵对应的每一行的每一个元素相加,获得新的矩阵(遍历两个矩阵对应的每一个行每个元素进行相加<第二步>,外部再遍历该矩阵的行数(循环的次数)<第一步>) 38 return Matrix([[a+b for a,b in zip(self.row_vector(i),another.row_vector(i))] 39 for i in range(self.row_num())]) 40 41 # 返回两个矩阵的减法结果 42 def __sub__(self, another): 43 assert self.shape() == another.shape(), \ 44 "Error in subtracting. Shape of matrix must be same." 45 return Matrix([[a - b for a, b in zip(self.row_vector(i), another.row_vector(i))] 46 for i in range(self.row_num())]) 47 48 #返回两个矩阵的乘法结果(矩阵乘以矩阵) 49 def dot(self,another): 50 if isinstance(another,Vector):#判断是否为向量:矩阵与向量的乘法 51 assert self.col_num() == len(another),\ 52 "Error in Matrix_Vector Multiplication." #矩阵与向量的乘法错误 53 return Vector([self.row_vector(i).dot(another) for i in range(self.row_num())]) 54 if isinstance(another,Matrix):#判断是否为矩阵:矩阵与矩阵的乘法 55 assert self.col_num() == another.row_num(),\ 56 "Error in Matrix-Matrix Multiplication." #矩阵与矩阵的乘法错误 57 # 将矩阵的每一行与另一矩阵的每一列进行向量间的点乘 58 return Matrix([[self.row_vector(i).dot(another.col_vector(j)) for j in range(another.col_num())] 59 for i in range(self.row_num())]) 60 61 #返回矩阵的数量乘结果(矩阵乘以数字):self * k 62 def __mul__(self, k): 63 #通过遍历每一行的每个元素e后分别乘以k<第一步>,外部再遍历该矩阵的行数(循环的次数)<第二步> 64 return Matrix([[e * k for e in self.row_vector(i)] 65 for i in range(self.row_num())]) 66 67 # 返回矩阵的数量乘结果(数字乘以矩阵):k * self 68 def __rmul__(self, k): 69 return self * k 70 71 #返回数量除法的结果矩阵:self / k 72 def __truediv__(self, k): 73 return (1 / k) * self 74 75 #返回矩阵取正的结果 76 def __pos__(self): 77 return 1 * self 78 79 #返回矩阵取负的结果 80 def __neg__(self): 81 return -1 * self 82 83 #返回矩阵的第index个行向量 84 def row_vector(self,index): 85 return Vector(self._values[index]) 86 87 # 返回矩阵的第index个列向量 88 def col_vector(self, index): 89 return Vector([row[index] for row in self._values]) 90 91 #返回矩阵pos位置的元素(根据元素的位置取元素值) :参数2:元组 92 def __getitem__(self, pos): 93 r,c = pos 94 return self._values[r][c] 95 96 #返回矩阵的元素个数 97 def size(self): 98 r,c = self.shape() 99 return r*c 100 101 #返回矩阵行数 102 def row_num(self): 103 return self.shape()[0] 104 105 __len__ = row_num 106 107 #返回矩阵列数 108 def col_num(self): 109 return self.shape()[1] 110 111 #返回矩阵形状:(行数,列数) 112 def shape(self): 113 return len(self._values),len(self._values[0]) 114 115 #矩阵展示 116 def __repr__(self): 117 return "Matrix({})".format(self._values) 118 119 __str__ = __repr__
2.在文件 GramSchmidtProcess.py 编写代码:新增矩阵的QR分解(qr)
1 from .Vector import Vector 2 from .Matrix import Matrix 3 from .LinearSystem import rank 4 5 6 #格拉姆-斯密特过程(参数为一组基-各个向量) 7 def gram_schmidt_process(basis): 8 #矩阵的秩 9 matrix = Matrix(basis)#初始化为矩阵 10 assert rank(matrix) == len(basis) #矩阵的秩 与这组基是否相等 11 12 #根据 #格拉姆-斯密特 公式分别计算向量P1、P2...再放入集合中 13 res = [basis[0]] 14 for i in range(1, len(basis)): 15 p = basis[i] 16 for r in res: 17 p = p - basis[i].dot(r) / r.dot(r) * r 18 res.append(p) 19 return res 20 21 22 #矩阵的QR分解 23 def qr(A): 24 # 判断A为方阵(行等于列) 25 assert A.row_num() == A.col_num(), "A must be square" 26 27 basis = [A.col_vector(i) for i in range(A.col_num())]#A的各个列向量 28 P = gram_schmidt_process(basis) # P为向量组(正交基) 29 Q = Matrix([v / v.norm() for v in P]).T()# 将P正交基变为标准正交基同时放入矩阵中去,再将该矩阵进行转置变为列向量的形式(标准正交矩阵Q) 30 R = Q.T().dot(A) # 标准正交矩阵的逆等于它的转置再点乘矩阵A(上三角矩阵R) 31 32 return Q, R
3.文件 main_qr.py 编写代码为:
1 from playLA.Matrix import Matrix 2 from playLA.GramSchmidtProcess import qr 3 4 if __name__ == "__main__": 5 6 #对矩阵进行QR分解 7 A1 = Matrix([[1,1,2], 8 [1,1,0], 9 [1,0,0]]) 10 11 Q1, R1 = qr(A1) 12 print("Q1 = {}".format(Q1)) 13 print("R1 = {}".format(R1)) 14 print("Q1.dot(R1) = {}".format(Q1.dot(R1)))#验证Q点乘R是否为 15 16 #对矩阵进行QR分解 17 A2 = Matrix([[2,-1,-1], 18 [2,0,2], 19 [2,-1,3]]) 20 21 Q2, R2 = qr(A2) 22 print("Q2 = {}".format(Q2)) 23 print("R2 = {}".format(R2)) 24 print("Q2.dot(R2) = {}".format(Q2.dot(R2)))#验证Q点乘R是否为
4.文件 main_qr.py 运行结果为:
1 /Users/liuxiaoming/PycharmProjects/LinearAlgebra/venv/bin/python /Applications/PyCharm.app/Contents/plugins/python/helpers/pydev/pydevconsole.py --mode=client --port=56341 2 import sys; print('Python %s on %s' % (sys.version, sys.platform)) 3 sys.path.extend(['/Users/liuxiaoming/PycharmProjects/LinearAlgebra']) 4 PyDev console: starting. 5 Python 3.8.2 (v3.8.2:7b3ab5921f, Feb 24 2020, 17:52:18) 6 [Clang 6.0 (clang-600.0.57)] on darwin 7 >>> runfile('/Users/liuxiaoming/PycharmProjects/LinearAlgebra/main_qr.py', wdir='/Users/liuxiaoming/PycharmProjects/LinearAlgebra') 8 Q1 = Matrix([[0.5773502691896258, 0.408248290463863, 0.7071067811865475], [0.5773502691896258, 0.408248290463863, -0.7071067811865475], [0.5773502691896258, -0.8164965809277259, 0.0]]) 9 R1 = Matrix([[1.7320508075688776, 1.1547005383792517, 1.1547005383792517], [1.1102230246251565e-16, 0.816496580927726, 0.816496580927726], [0.0, 0.0, 1.414213562373095]]) 10 Q1.dot(R1) = Matrix([[1.0000000000000002, 1.0000000000000002, 2.0], [1.0000000000000002, 1.0000000000000002, 4.440892098500626e-16], [1.0000000000000002, 2.220446049250313e-16, 2.220446049250313e-16]]) 11 Q2 = Matrix([[0.5773502691896258, -0.408248290463863, -0.7071067811865475], [0.5773502691896258, 0.8164965809277259, 1.1775693440128314e-16], [0.5773502691896258, -0.408248290463863, 0.7071067811865476]]) 12 R2 = Matrix([[3.4641016151377553, -1.1547005383792517, 2.3094010767585034], [-2.220446049250313e-16, 0.816496580927726, 0.8164965809277258], [4.440892098500626e-16, -1.1102230246251565e-16, 2.8284271247461907]]) 13 Q2.dot(R2) = Matrix([[2.0, -1.0000000000000002, -1.0], [2.0000000000000004, -2.220446049250313e-16, 2.0000000000000004], [2.000000000000001, -1.0000000000000002, 3.000000000000001]])
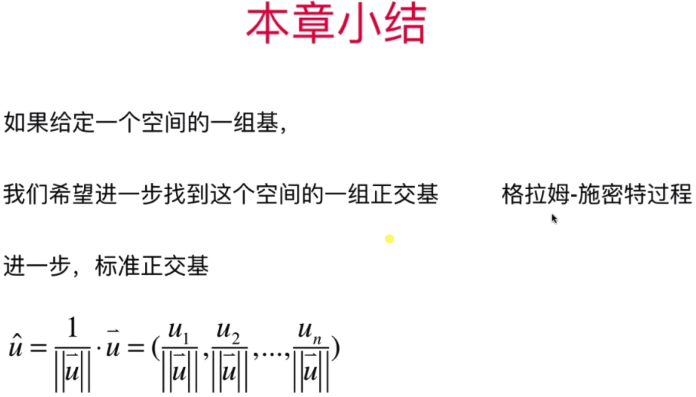
- 本章小结和更多和投影相关的话题