人工智能必备数学知识学习笔记9:初等矩阵和矩阵的可逆性
- 线性系统与矩阵的逆


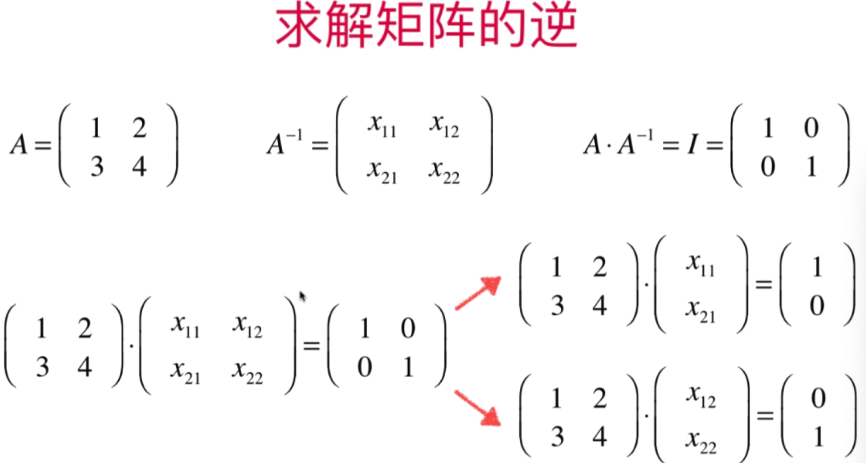

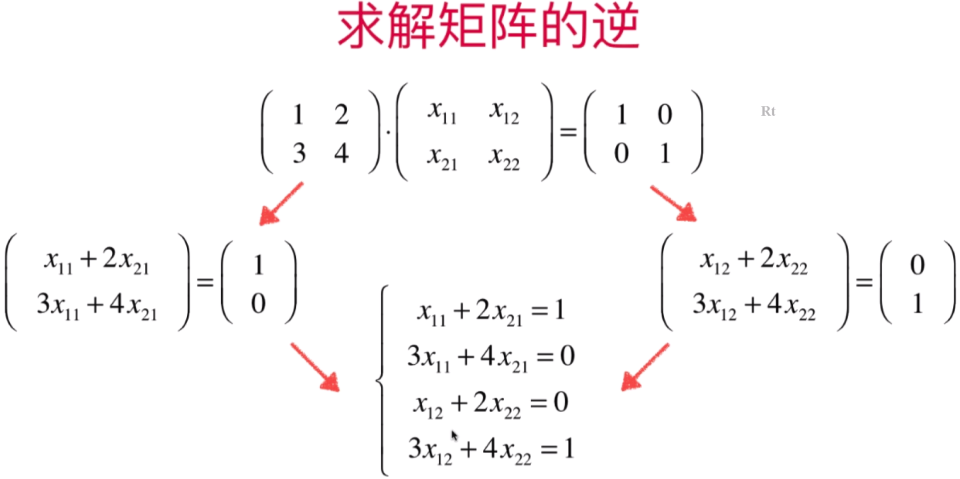
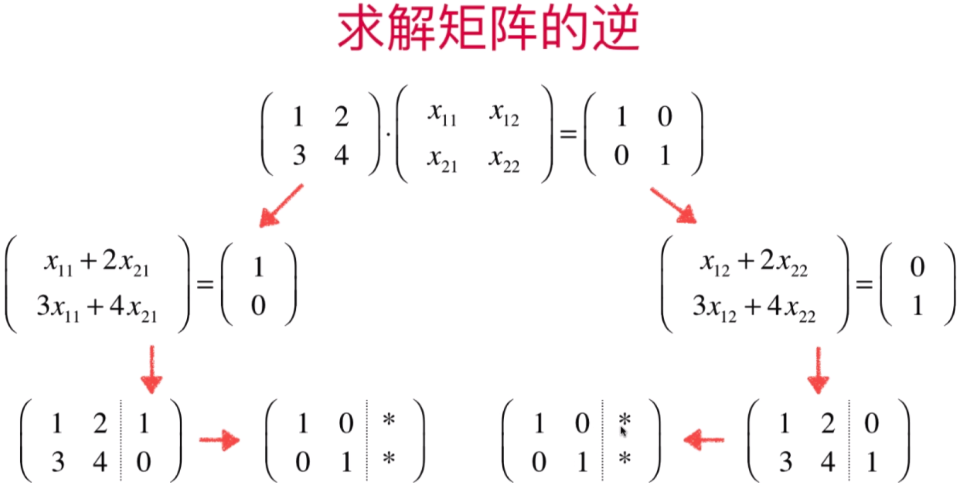
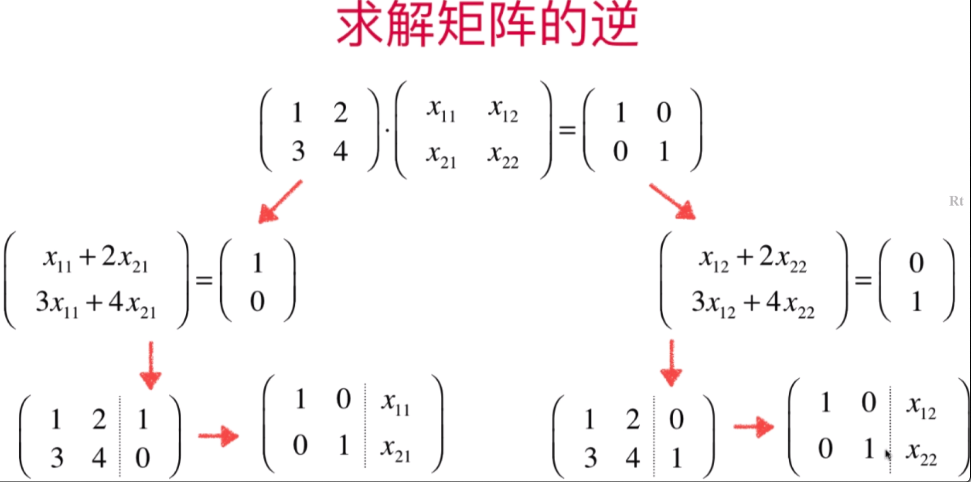





代码实现:
1.在文件 Matrix.py 中使用identity(单位矩阵方法)
1 #矩阵类 2 from playLA.Vector import Vector 3 4 5 class Matrix: 6 # 参数2:二维数组 7 def __init__(self, list2d): 8 self._values = [row[:] for row in list2d]#将数组变为矩阵 9 10 #矩阵类方法:返回一个r行c列的零矩阵:参数1:为零的类对象 11 @classmethod 12 def zero(cls,r,c): 13 return cls([[0] * c for _ in range(r)]) #创建一个r行c列为零的一个列表 14 15 #单位矩阵类方法:返回一个n行n列的单位矩阵 16 @classmethod 17 def identity(cls, n): 18 m = [[0] * n for _ in range(n)] #此处 m 代表有 n 行,每一行有 n 个 0 19 for i in range(n): 20 m[i][i] = 1 #此处代表将矩阵 m 的 第i行的第i个元素赋值为1 21 return cls(m) 22 23 #返回矩阵的转置矩阵 24 def T(self): 25 #将每一行的相同位置(每一列)元素提取出来变为行组成新的矩阵 26 return Matrix([[e for e in self.col_vector(i)] 27 for i in range(self.col_num())]) 28 29 #返回两个矩阵的加法结果 30 def __add__(self, another): 31 # 校验两个矩阵的形状为一致(行数、列数一致) 32 assert self.shape() == another.shape(), \ 33 "Error in adding. Shape of matrix must be same." 34 # 根据矩阵的加法公式:两个矩阵对应的每一行的每一个元素相加,获得新的矩阵(遍历两个矩阵对应的每一个行每个元素进行相加<第二步>,外部再遍历该矩阵的行数(循环的次数)<第一步>) 35 return Matrix([[a+b for a,b in zip(self.row_vector(i),another.row_vector(i))] 36 for i in range(self.row_num())]) 37 38 # 返回两个矩阵的减法结果 39 def __sub__(self, another): 40 assert self.shape() == another.shape(), \ 41 "Error in subtracting. Shape of matrix must be same." 42 return Matrix([[a - b for a, b in zip(self.row_vector(i), another.row_vector(i))] 43 for i in range(self.row_num())]) 44 45 #返回两个矩阵的乘法结果(矩阵乘以矩阵) 46 def dot(self,another): 47 if isinstance(another,Vector):#判断是否为向量:矩阵与向量的乘法 48 assert self.col_num() == len(another),\ 49 "Error in Matrix_Vector Multiplication." #矩阵与向量的乘法错误 50 return Vector([self.row_vector(i).dot(another) for i in range(self.row_num())]) 51 if isinstance(another,Matrix):#判断是否为矩阵:矩阵与矩阵的乘法 52 assert self.col_num() == another.row_num(),\ 53 "Error in Matrix-Matrix Multiplication." #矩阵与矩阵的乘法错误 54 # 将矩阵的每一行与另一矩阵的每一列进行向量间的点乘 55 return Matrix([[self.row_vector(i).dot(another.col_vector(j)) for j in range(another.col_num())] 56 for i in range(self.row_num())]) 57 58 #返回矩阵的数量乘结果(矩阵乘以数字):self * k 59 def __mul__(self, k): 60 #通过遍历每一行的每个元素e后分别乘以k<第一步>,外部再遍历该矩阵的行数(循环的次数)<第二步> 61 return Matrix([[e * k for e in self.row_vector(i)] 62 for i in range(self.row_num())]) 63 64 # 返回矩阵的数量乘结果(数字乘以矩阵):k * self 65 def __rmul__(self, k): 66 return self * k 67 68 #返回数量除法的结果矩阵:self / k 69 def __truediv__(self, k): 70 return (1 / k) * self 71 72 #返回矩阵取正的结果 73 def __pos__(self): 74 return 1 * self 75 76 #返回矩阵取负的结果 77 def __neg__(self): 78 return -1 * self 79 80 #返回矩阵的第index个行向量 81 def row_vector(self,index): 82 return Vector(self._values[index]) 83 84 # 返回矩阵的第index个列向量 85 def col_vector(self, index): 86 return Vector([row[index] for row in self._values]) 87 88 #返回矩阵pos位置的元素(根据元素的位置取元素值) :参数2:元组 89 def __getitem__(self, pos): 90 r,c = pos 91 return self._values[r][c] 92 93 #返回矩阵的元素个数 94 def size(self): 95 r,c = self.shape() 96 return r*c 97 98 #返回矩阵行数 99 def row_num(self): 100 return self.shape()[0] 101 102 __len__ = row_num 103 104 #返回矩阵列数 105 def col_num(self): 106 return self.shape()[1] 107 108 #返回矩阵形状:(行数,列数) 109 def shape(self): 110 return len(self._values),len(self._values[0]) 111 112 #矩阵展示 113 def __repr__(self): 114 return "Matrix({})".format(self._values) 115 116 __str__ = __repr__
2.在文件 LinearSystem.py 中编写:
2.1修改__init__中增加两个条件分别判断参数b是列向量还是矩阵
2.2增加 求增广矩阵的逆方法(inv)
1 from playLA.Matrix import Matrix 2 from playLA.Vector import Vector 3 from playLA._global import is_zero 4 5 6 #线性系统 7 class LinearSystem: 8 9 #初始化函数:参数A:增广矩阵的等号左边的系数 参数b:增广矩阵的等号右边的值(方程右边的结果) 10 def __init__(self, A, b): 11 #判断矩阵A的行数是否等于b的列数 12 assert A.row_num() == len(b),\ 13 "row number of A must be equal to the length of b" 14 self._m = A.row_num()#行数 15 self._n = A.col_num()#列数 16 17 if isinstance(b, Vector):#如果等号右侧方程结果为列向量时 18 #增广矩阵 19 self.Ab = [Vector(A.row_vector(i).underlying_list() + [b[i]]) 20 for i in range(self._m)] 21 22 if isinstance(b, Matrix):#如果等号右侧方程结果为单位矩阵时 23 #增广矩阵 24 self.Ab = [Vector(A.row_vector(i).underlying_list() + b.row_vector(i).underlying_list()) 25 for i in range(self._m)] 26 #主元 27 self.pivots = [] 28 29 #寻找最大主源系数 30 def _max_row(self, index_i, index_j, n): 31 best, ret = self.Ab[index_i][index_j], index_i #存储第index行index列的元素值与当前index的值 32 for i in range(index_i + 1, n): #从index+1开始一直遍历到n 33 if self.Ab[i][index_j] > best: 34 best, ret = self.Ab[i][index_j], i 35 return ret 36 37 #高斯—约旦消元法-前向过程 38 def _forward(self): 39 40 i,k = 0,0 41 while i < self._m and k < self._n: 42 #看Ab[i][k]位置是否为主元 43 max_row = self._max_row(i, k, self._m)#寻找最大主源系数的行数 44 self.Ab[i], self.Ab[max_row] = self.Ab[max_row],self.Ab[i] #行交换操作 45 46 if is_zero(self.Ab[i][k]):#判断此时该值是否为0 47 k += 1 48 else: 49 #将主元归为一 50 self.Ab[i] = self.Ab[i] / self.Ab[i][k] 51 #将当前主源下的所有行对应主源列的元素全部归为0 :也就是第一次循环会将该主源下的所有对应列变为0,第二次循环会将第二次主源列下的所有对应列变为0 52 for j in range(i + 1, self._m): 53 self.Ab[j] =self.Ab[j] -self.Ab[j][k] * self.Ab[i]#该主源行下的所有行减去主源行 54 self.pivots.append(k) 55 i += 1 56 57 #高斯-约旦消元法-后向过程 58 def _backward(self): 59 n = len(self.pivots) 60 #n = self._m #行数 61 for i in range(n-1, -1, -1): #反向遍历且 从参数1的位置遍历到参数2的位置,也就是从倒数第一个位置遍历到第一个位置,参数3为步长(遍历的方向及单位) 62 k = self.pivots[i] 63 #Ab[i][k]为主源 64 for j in range(i-1, -1, -1): 65 self.Ab[j] = self.Ab[j] - self.Ab[j][k] * self.Ab[i]#该主源行上的所有行减去主源行 66 67 #高斯-约旦消元法:如果有解,返回True;如果没有解,返回False 68 def gauss_jordan_elimination(self): 69 # 高斯—约旦消元法-前向过程 70 self._forward() 71 # 高斯-约旦消元法-后向过程 72 self._backward() 73 for i in range(len(self.pivots), self._m):#此处为最后一行的非零行下一行的全零行的结果值不为零的判断 0.0 0.0 | 5.0 74 if not is_zero(self.Ab[i][-1]): 75 return False 76 return True 77 78 # 打印结果(求每个未知数的值) 79 def fancy_print(self): 80 for i in range(self._m): 81 print(" ".join(str(self.Ab[i][j]) for j in range(self._n)),end=" ") 82 print("|",self.Ab[i][-1]) 83 84 85 #求增广矩阵的逆 86 def inv(A): 87 88 if A.row_num() != A.col_num():#判断矩阵行是否等于列,若不等于无解 89 return None 90 91 n = A.row_num() # TODO:A.row_num 无括号代表方法,类型为method A.row_num() 有括号代表具体的返回值 92 print(n,type(n)) 93 ls = LinearSystem(A, Matrix.identity(n))#实例化一个线性系统(创建一个增广矩阵) 94 if not ls.gauss_jordan_elimination(): #判断是否有逆矩阵(是否有解) 95 return None 96 97 invA = [[row[i] for i in range(n, n*n)] for row in ls.Ab] #将右侧的单位矩阵拼接到矩阵中 98 99 return Matrix(invA)
3.在文件 main_linear_system.py 编写:求矩阵的逆
1 from playLA.Matrix import Matrix 2 from playLA.Vector import Vector 3 from playLA.LinearSystem import LinearSystem 4 from playLA.LinearSystem import inv 5 6 if __name__ == "__main__": 7 8 # 高斯—约旦消元法 9 A = Matrix([[1,2,4],[3,7,2],[2,3,3]]) 10 b = Vector([7,-11,1]) 11 ls = LinearSystem(A,b) #线性系统赋值成一个增广矩阵 12 ls.gauss_jordan_elimination() #高斯—约旦消元 13 ls.fancy_print() #打印出结果(求每个未知数的值) 14 print("-" * 50)#分隔线 15 16 # 高斯—约旦消元法 17 A2 = Matrix([[1, -3, 5], [2, -1, -3], [3, 1, 4]]) 18 b2 = Vector([-9, 19, 13]) 19 ls2 = LinearSystem(A2, b2) # 线性系统赋值成一个增广矩阵 20 ls2.gauss_jordan_elimination() # 高斯—约旦消元 21 ls2.fancy_print() # 打印出结果(求每个未知数的值) 22 print("-" * 50) # 分隔线 23 24 # 高斯—约旦消元法 25 A3 = Matrix([[1, 2, -2], [2, -3, 1], [3, -1, 3]]) 26 b3 = Vector([6, -10, -16]) 27 ls3 = LinearSystem(A3, b3) # 线性系统赋值成一个增广矩阵 28 ls3.gauss_jordan_elimination() # 高斯—约旦消元 29 ls3.fancy_print() # 打印出结果(求每个未知数的值) 30 print("-" * 50) # 分隔线 31 32 # 高斯—约旦消元法 33 A4 = Matrix([[3, 1, -2], [5, -3, 10], [7, 4, 16]]) 34 b4 = Vector([4, 32, 13]) 35 ls4 = LinearSystem(A4, b4) # 线性系统赋值成一个增广矩阵 36 ls4.gauss_jordan_elimination() # 高斯—约旦消元 37 ls4.fancy_print() # 打印出结果(求每个未知数的值) 38 print("-" * 50) # 分隔线 39 40 # 高斯—约旦消元法 41 A5 = Matrix([[6, -3, 2], [5, 1, 12], [8, 5, 1]]) 42 b5 = Vector([31, 36, 11]) 43 ls5 = LinearSystem(A5, b5) # 线性系统赋值成一个增广矩阵 44 ls5.gauss_jordan_elimination() # 高斯—约旦消元 45 ls5.fancy_print() # 打印出结果(求每个未知数的值) 46 print("-" * 50) # 分隔线 47 48 # 高斯—约旦消元法 49 A6 = Matrix([[1, 1, 1], [1, -1, -1], [2, 1, 5]]) 50 b6 = Vector([3, -1, 8]) 51 ls6 = LinearSystem(A6, b6) # 线性系统赋值成一个增广矩阵 52 ls6.gauss_jordan_elimination() # 高斯—约旦消元 53 ls6.fancy_print() # 打印出结果(求每个未知数的值) 54 print("-" * 50) # 分隔线 55 56 # 高斯—约旦消元法 57 A7 = Matrix([[1, -1, 2, 0, 3], 58 [-1, 1, 0, 2, -5], 59 [1, -1, 4, 2, 4], 60 [-2, 2, -5, -1, -3]]) 61 b7 = Vector([1, 5, 13, -1]) 62 ls7 = LinearSystem(A7, b7) # 线性系统赋值成一个增广矩阵 63 ls7.gauss_jordan_elimination() # 高斯—约旦消元 64 ls7.fancy_print() # 打印出结果(求每个未知数的值) 65 print("-" * 50) # 分隔线 66 print(ls7.pivots) #查看主源列数值 (从零开始算) 67 68 # 高斯—约旦消元法 69 A8 = Matrix([[2, 2], 70 [2, 1], 71 [1, 2]]) 72 b8 = Vector([3, 2.5, 7]) 73 ls8 = LinearSystem(A8, b8) # 线性系统赋值成一个增广矩阵 74 if not ls8.gauss_jordan_elimination(): 75 print("主元:",ls8.pivots 76 ,len(ls8.pivots)) # 查看主源列数值 (从零开始算) 77 print("No Solution!") 78 79 ls8.fancy_print() # 打印出结果(求每个未知数的值) 80 print("-" * 50) # 分隔线 81 82 #求矩阵的逆 83 A = Matrix([[1,2],[3,4]]) 84 invA = inv(A) 85 print("invA = {}".format(invA)) 86 print("A.dot(invA) = {}".format(A.dot(invA))) 87 print("invA.dot(A) = {}".format(invA.dot(A)))
4.运行文件 main_linear_system.py 结果为:
1 /Users/liuxiaoming/PycharmProjects/LinearAlgebra/venv/bin/python /Users/liuxiaoming/PycharmProjects/LinearAlgebra/main_linear_system.py 2 1.0 0.0 0.0 | -1.0 3 -0.0 1.0 0.0 | -2.0 4 -0.0 -0.0 1.0 | 3.0 5 -------------------------------------------------- 6 1.0 0.0 0.0 | 6.853333333333333 7 -0.0 1.0 0.0 | 1.506666666666665 8 0.0 0.0 1.0 | -2.266666666666666 9 -------------------------------------------------- 10 1.0 0.0 0.0 | -1.9999999999999998 11 0.0 1.0 0.0 | 1.0 12 -0.0 -0.0 1.0 | -3.0 13 -------------------------------------------------- 14 1.0 0.0 0.0 | 2.9999999999999996 15 -0.0 1.0 0.0 | -3.9999999999999996 16 0.0 0.0 1.0 | 0.4999999999999999 17 -------------------------------------------------- 18 1.0 0.0 0.0 | 3.0 19 -0.0 1.0 0.0 | -3.0 20 -0.0 -0.0 1.0 | 2.0 21 -------------------------------------------------- 22 1.0 0.0 0.0 | 1.0 23 0.0 1.0 0.0 | 1.0 24 -0.0 -0.0 1.0 | 1.0 25 -------------------------------------------------- 26 1.0 -1.0 0.0 -2.0 0.0 | -15.0 27 0.0 0.0 1.0 1.0 0.0 | 5.0 28 0.0 0.0 0.0 0.0 1.0 | 2.0 29 0.0 0.0 0.0 0.0 0.0 | 0.0 30 -------------------------------------------------- 31 [0, 2, 4] 32 主元: [0, 1] 2 33 No Solution! 34 1.0 0.0 | -4.0 35 0.0 1.0 | 5.5 36 0.0 0.0 | 5.0 37 -------------------------------------------------- 38 2 <class 'int'> 39 invA = Matrix([[-1.9999999999999996, 0.9999999999999998], [1.4999999999999998, -0.4999999999999999]]) 40 A.dot(invA) = Matrix([[1.0, 0.0], [8.881784197001252e-16, 0.9999999999999996]]) 41 invA.dot(A) = Matrix([[0.9999999999999996, 0.0], [2.220446049250313e-16, 1.0]]) 42 43 Process finished with exit code 0
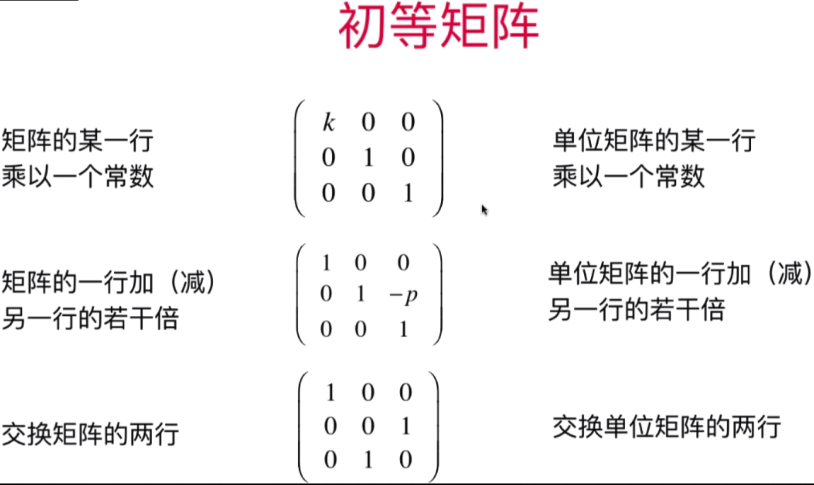
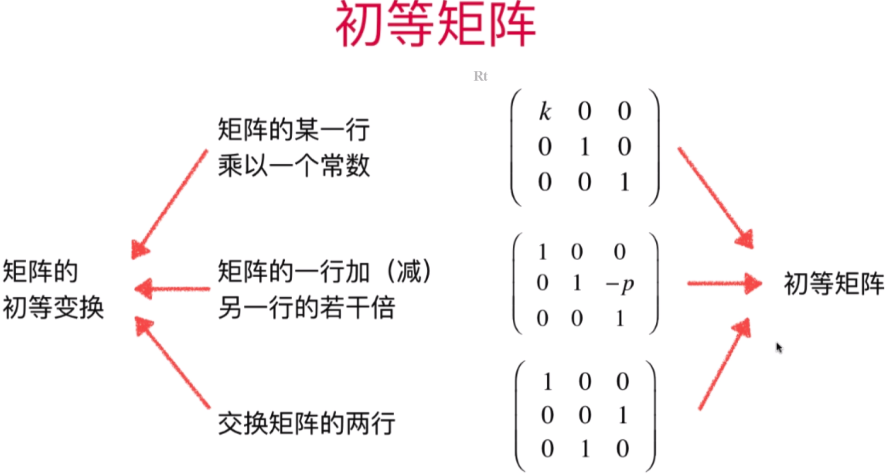
- 初等矩阵






将 d e f 与 g h i 则将单位矩阵第二行与第三行调换位置即可

单位矩阵中每一行中的1来控制第二行的列中每个元素的位置,也就是说单位矩阵每一行乘以后面矩阵的列(单位矩阵来控制后面矩阵的行列展示)
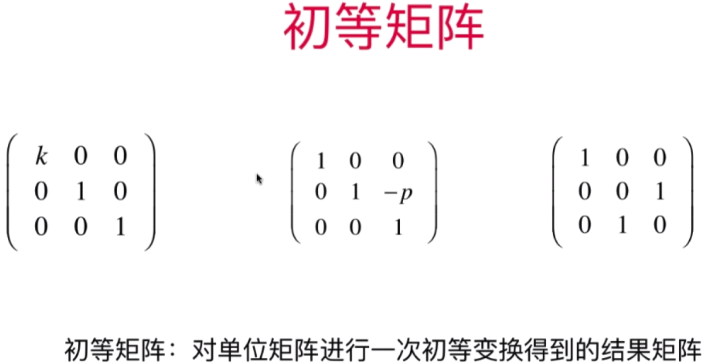
行最简形式:rref

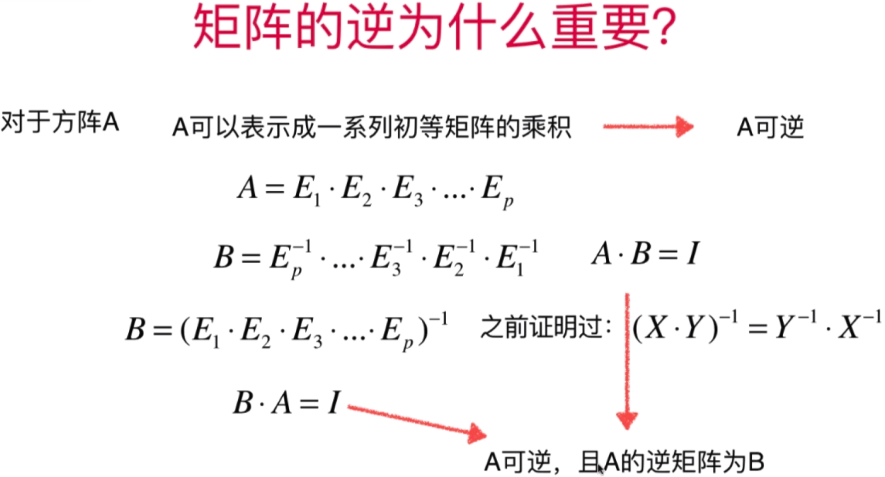
- 从初等矩阵到矩阵的逆


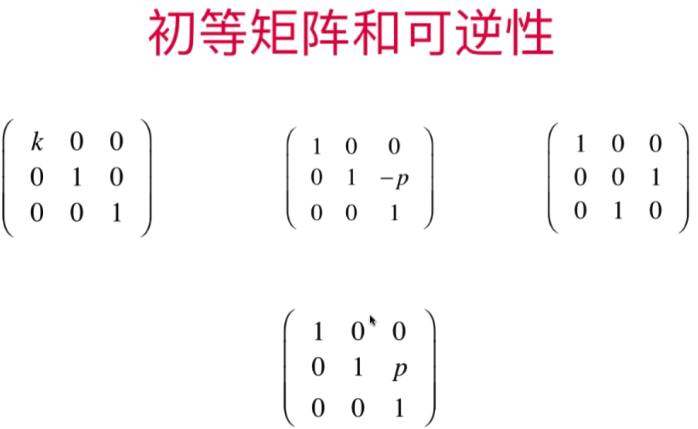
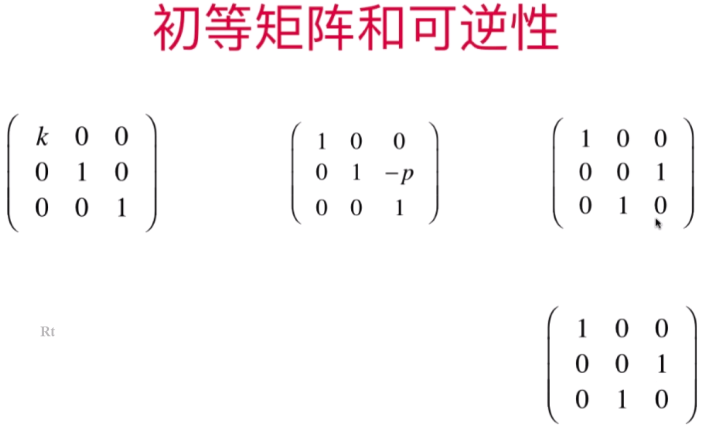

E为初等变换:高斯-约旦消元法的操作都叫E

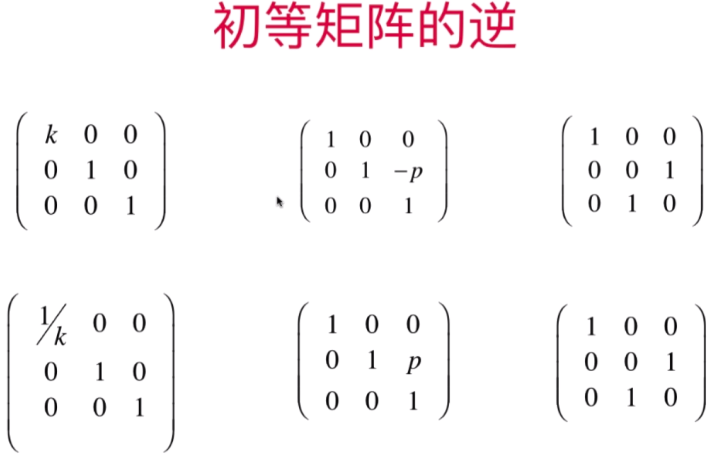
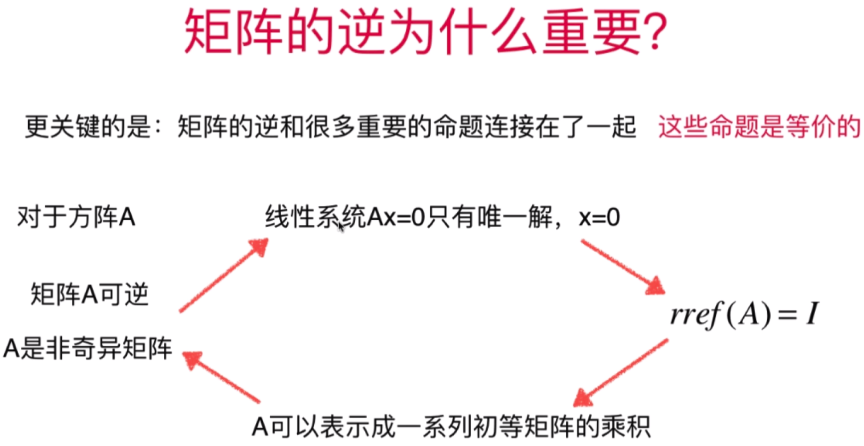
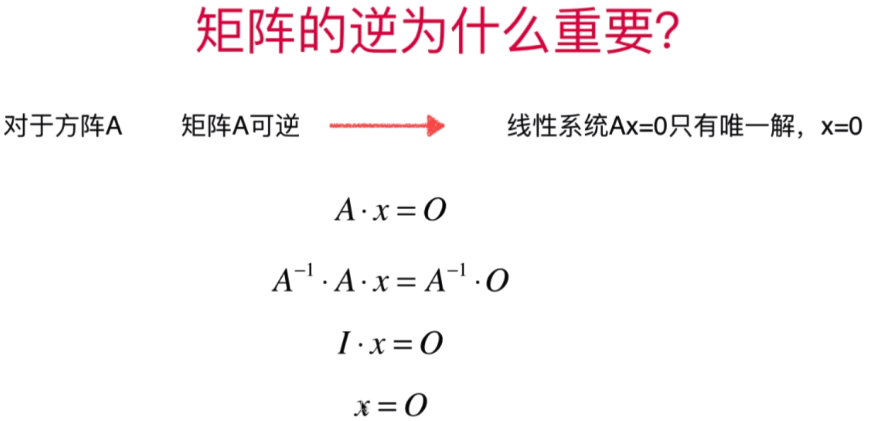
- 为什么矩阵的逆这么重要

A-1 * A = I (单位矩阵) I * x = x


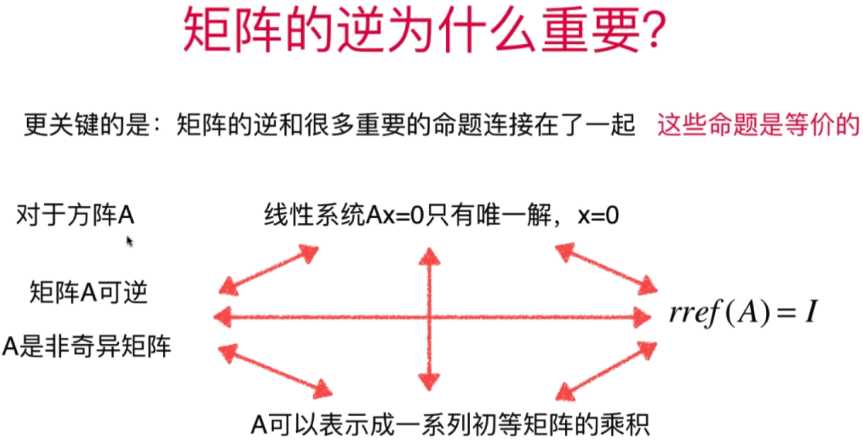




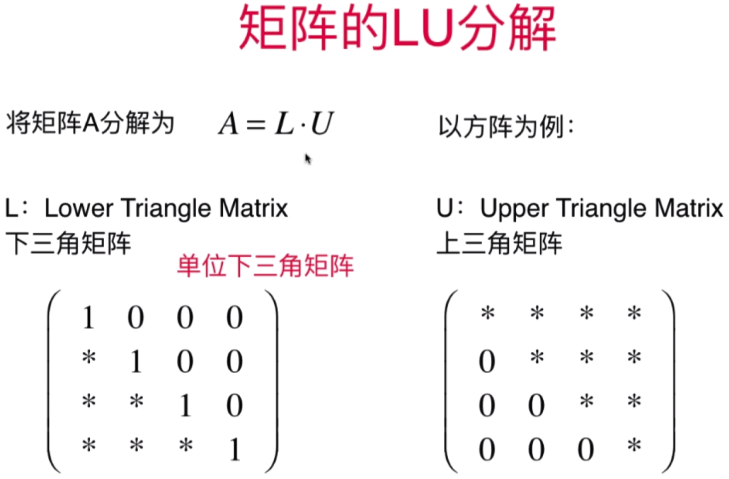
- 矩阵的LU分解


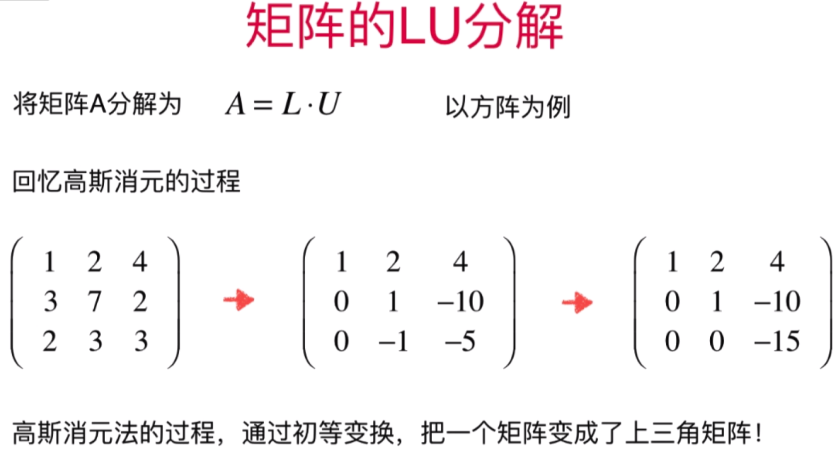

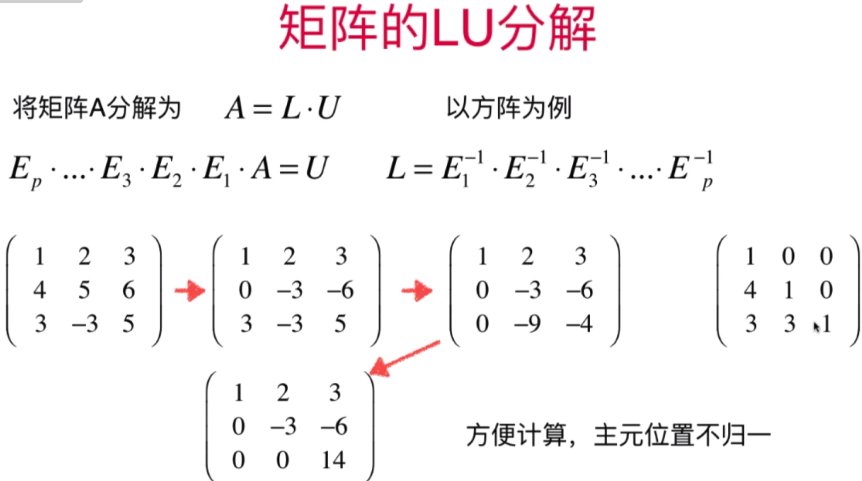



代码实现:
1.调用文件 _global.py
1 #包内部使用的全局变量 2 3 EPSILON = 1e-8 #精度范围为 1除以10的八次方 4 5 6 #判断x的绝对值是否小于精度范围(EPSILON) 7 def is_zero(x): 8 return abs(x) < EPSILON 9 10 11 #判断a和b两个浮点值是否相等 12 def is_equal(a,b): 13 return abs(a - b) < EPSILON #判断差值的绝对值是否在精度范围内
2.调用文件 Matrix.py
1 #矩阵类 2 from playLA.Vector import Vector 3 4 5 class Matrix: 6 # 参数2:二维数组 7 def __init__(self, list2d): 8 self._values = [row[:] for row in list2d]#将数组变为矩阵 9 10 #矩阵类方法:返回一个r行c列的零矩阵:参数1:为零的类对象 11 @classmethod 12 def zero(cls,r,c): 13 return cls([[0] * c for _ in range(r)]) #创建一个r行c列为零的一个列表 14 15 #单位矩阵类方法:返回一个n行n列的单位矩阵 16 @classmethod 17 def identity(cls, n): 18 m = [[0] * n for _ in range(n)] #此处 m 代表有 n 行,每一行有 n 个 0 19 for i in range(n): 20 m[i][i] = 1 #此处代表将矩阵 m 的 第i行的第i个元素赋值为1 21 return cls(m) 22 23 #返回矩阵的转置矩阵 24 def T(self): 25 #将每一行的相同位置(每一列)元素提取出来变为行组成新的矩阵 26 return Matrix([[e for e in self.col_vector(i)] 27 for i in range(self.col_num())]) 28 29 #返回两个矩阵的加法结果 30 def __add__(self, another): 31 # 校验两个矩阵的形状为一致(行数、列数一致) 32 assert self.shape() == another.shape(), \ 33 "Error in adding. Shape of matrix must be same." 34 # 根据矩阵的加法公式:两个矩阵对应的每一行的每一个元素相加,获得新的矩阵(遍历两个矩阵对应的每一个行每个元素进行相加<第二步>,外部再遍历该矩阵的行数(循环的次数)<第一步>) 35 return Matrix([[a+b for a,b in zip(self.row_vector(i),another.row_vector(i))] 36 for i in range(self.row_num())]) 37 38 # 返回两个矩阵的减法结果 39 def __sub__(self, another): 40 assert self.shape() == another.shape(), \ 41 "Error in subtracting. Shape of matrix must be same." 42 return Matrix([[a - b for a, b in zip(self.row_vector(i), another.row_vector(i))] 43 for i in range(self.row_num())]) 44 45 #返回两个矩阵的乘法结果(矩阵乘以矩阵) 46 def dot(self,another): 47 if isinstance(another,Vector):#判断是否为向量:矩阵与向量的乘法 48 assert self.col_num() == len(another),\ 49 "Error in Matrix_Vector Multiplication." #矩阵与向量的乘法错误 50 return Vector([self.row_vector(i).dot(another) for i in range(self.row_num())]) 51 if isinstance(another,Matrix):#判断是否为矩阵:矩阵与矩阵的乘法 52 assert self.col_num() == another.row_num(),\ 53 "Error in Matrix-Matrix Multiplication." #矩阵与矩阵的乘法错误 54 # 将矩阵的每一行与另一矩阵的每一列进行向量间的点乘 55 return Matrix([[self.row_vector(i).dot(another.col_vector(j)) for j in range(another.col_num())] 56 for i in range(self.row_num())]) 57 58 #返回矩阵的数量乘结果(矩阵乘以数字):self * k 59 def __mul__(self, k): 60 #通过遍历每一行的每个元素e后分别乘以k<第一步>,外部再遍历该矩阵的行数(循环的次数)<第二步> 61 return Matrix([[e * k for e in self.row_vector(i)] 62 for i in range(self.row_num())]) 63 64 # 返回矩阵的数量乘结果(数字乘以矩阵):k * self 65 def __rmul__(self, k): 66 return self * k 67 68 #返回数量除法的结果矩阵:self / k 69 def __truediv__(self, k): 70 return (1 / k) * self 71 72 #返回矩阵取正的结果 73 def __pos__(self): 74 return 1 * self 75 76 #返回矩阵取负的结果 77 def __neg__(self): 78 return -1 * self 79 80 #返回矩阵的第index个行向量 81 def row_vector(self,index): 82 return Vector(self._values[index]) 83 84 # 返回矩阵的第index个列向量 85 def col_vector(self, index): 86 return Vector([row[index] for row in self._values]) 87 88 #返回矩阵pos位置的元素(根据元素的位置取元素值) :参数2:元组 89 def __getitem__(self, pos): 90 r,c = pos 91 return self._values[r][c] 92 93 #返回矩阵的元素个数 94 def size(self): 95 r,c = self.shape() 96 return r*c 97 98 #返回矩阵行数 99 def row_num(self): 100 return self.shape()[0] 101 102 __len__ = row_num 103 104 #返回矩阵列数 105 def col_num(self): 106 return self.shape()[1] 107 108 #返回矩阵形状:(行数,列数) 109 def shape(self): 110 return len(self._values),len(self._values[0]) 111 112 #矩阵展示 113 def __repr__(self): 114 return "Matrix({})".format(self._values) 115 116 __str__ = __repr__
3.文件 LU 编写代码为:
1 from .Matrix import Matrix 2 from .Vector import Vector 3 from ._global import is_zero 4 5 #矩阵的LU分解 6 7 def lu(martrix): 8 9 assert martrix.row_num() == martrix.col_num(), "matrix must be a square matrix" #判断矩阵是否行数等于列数(是否为方阵),不是的话错误提示"矩阵必须为方阵" 10 11 n = martrix.row_num() #矩阵行数 12 A = [martrix.row_vector(i) for i in range(n)] # 向量列表 matrix (上三角矩阵) 13 L = [[1.0 if i == j else 0.0 for i in range(n)] for j in range(n)] #下三角矩阵(初始化为单位矩阵) i = 为列 j = 为行 14 15 #高斯消元过程(此处为LU分解 无需将主源行归一处理) 16 for i in range(n): #遍历每一行主元下的处理 17 18 #看A[i][i]是否为主元 19 if is_zero(A[i][i]): 20 return None, None 21 else: 22 for j in range(i + 1, n): #将主元所在列以下行对应的元素化为0 23 p = A[j][i] / A[i][i] #倍数是 下面对应列的元素除以主元 24 A[j] = A[j] - p * A[i] #下一行 减去 主元行的倍数 25 L[j][i] = p #求取 L 元素的逆就为p(求取初等变换的逆) 26 return Matrix(L), Matrix([A[i].underlying_list() for i in range(n)]) #分别返回 矩阵 L;向量的列表 A 封装成列表的列表
4.文件 main_lu.py 编写代码为:
1 from playLA.Matrix import Matrix 2 from playLA.LU import lu 3 4 if __name__ == "__main__": 5 6 A = Matrix([[1,2,3],[4,5,6],[3,-3,5]]) #创建矩阵 A 7 L, U = lu(A) #进行对A矩阵进行分解成L、U 8 print("L = {}".format(L)) 9 print("U = {}".format(U)) 10 print("L.dot(U) = {}".format(L.dot(U)))
5.文件 main_lu.py 运行结果为:
1 /Users/liuxiaoming/PycharmProjects/LinearAlgebra/venv/bin/python /Applications/PyCharm.app/Contents/plugins/python/helpers/pydev/pydevconsole.py --mode=client --port=57795 2 import sys; print('Python %s on %s' % (sys.version, sys.platform)) 3 sys.path.extend(['/Users/liuxiaoming/PycharmProjects/LinearAlgebra']) 4 PyDev console: starting. 5 Python 3.8.2 (v3.8.2:7b3ab5921f, Feb 24 2020, 17:52:18) 6 [Clang 6.0 (clang-600.0.57)] on darwin 7 runfile('/Users/liuxiaoming/PycharmProjects/LinearAlgebra/main_lu.py', wdir='/Users/liuxiaoming/PycharmProjects/LinearAlgebra') 8 L = Matrix([[1.0, 0.0, 0.0], [4.0, 1.0, 0.0], [3.0, 3.0, 1.0]]) 9 U = Matrix([[1, 2, 3], [0.0, -3.0, -6.0], [0.0, 0.0, 14.0]]) 10 L.dot(U) = Matrix([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [3.0, -3.0, 5.0]])
- 非方阵的LU分解,矩阵的LDU分解和PLU分解

方阵:

非方阵分解:
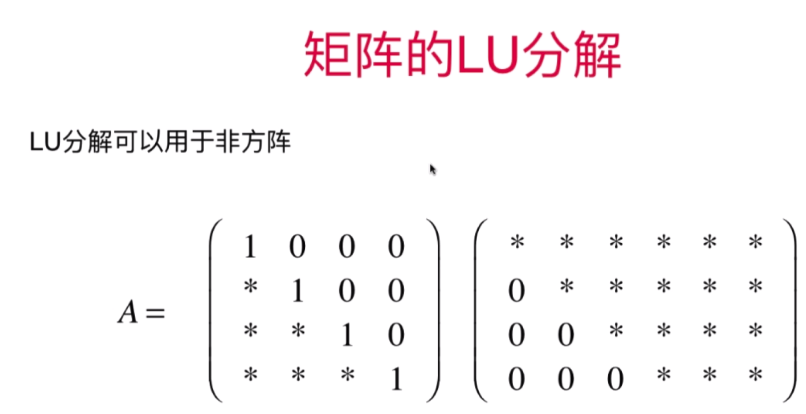


对角矩阵(D):取对角线上的数字,其他元素均为0
根据矩阵A的第二行与第三行需要交换位置,故单位矩阵的逆矩阵的元素也需要调换位置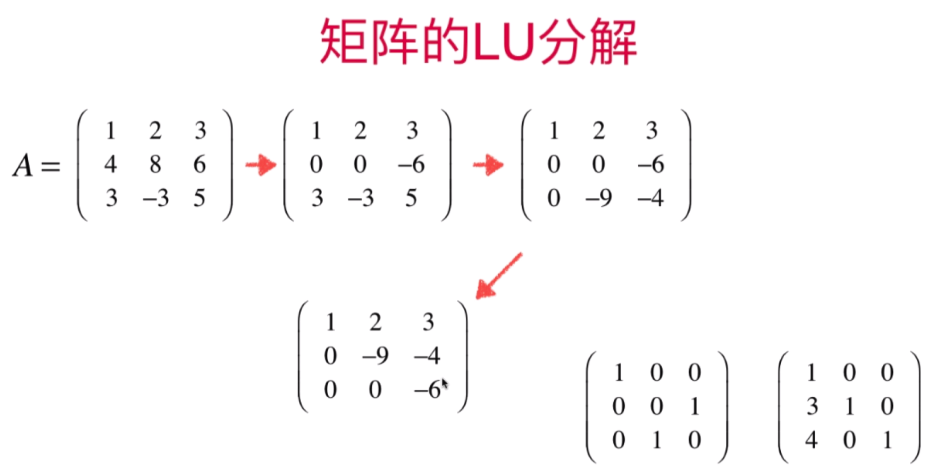
针对需要换行的矩阵:则多出置换矩阵P,称为矩阵的PLU分解
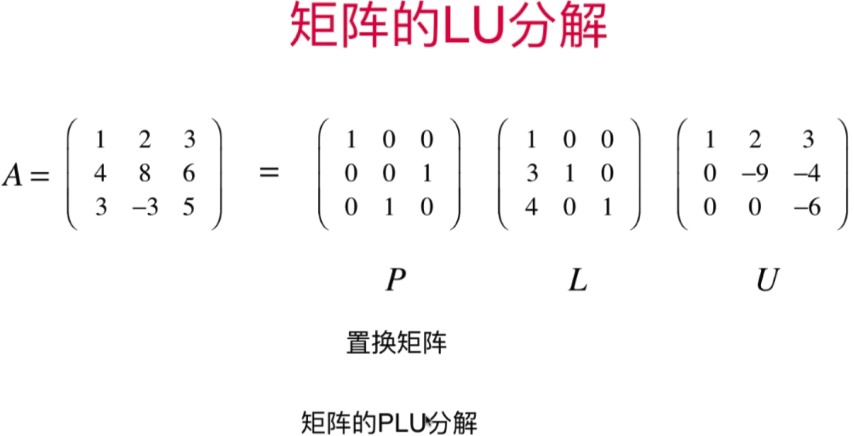
- 矩阵的PLU分解和再看矩阵的乘法



行乘以列(列交换):结果矩阵为:置换原矩阵的列
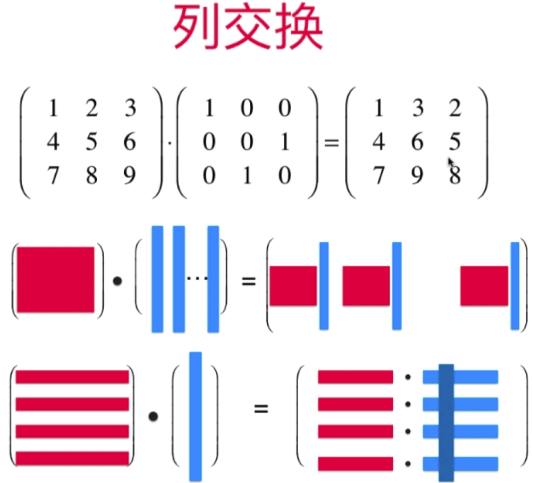
行乘以矩阵(行交换):结果矩阵为:置换原矩阵的行
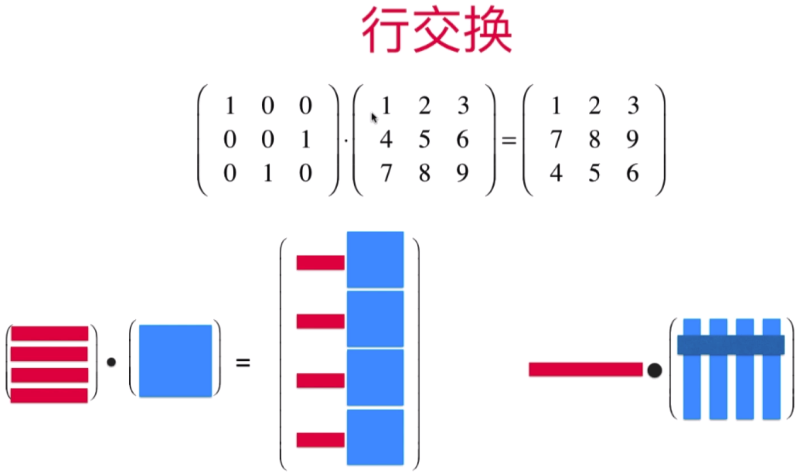
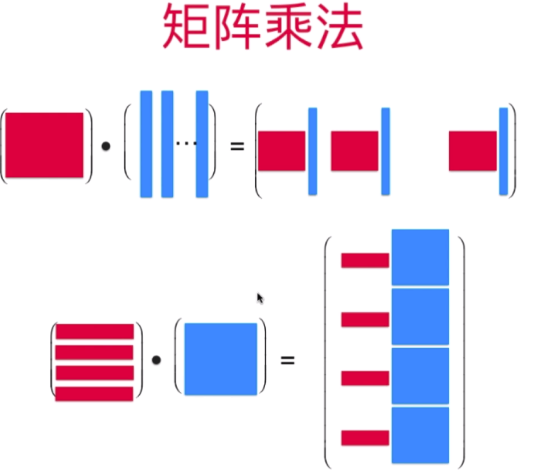
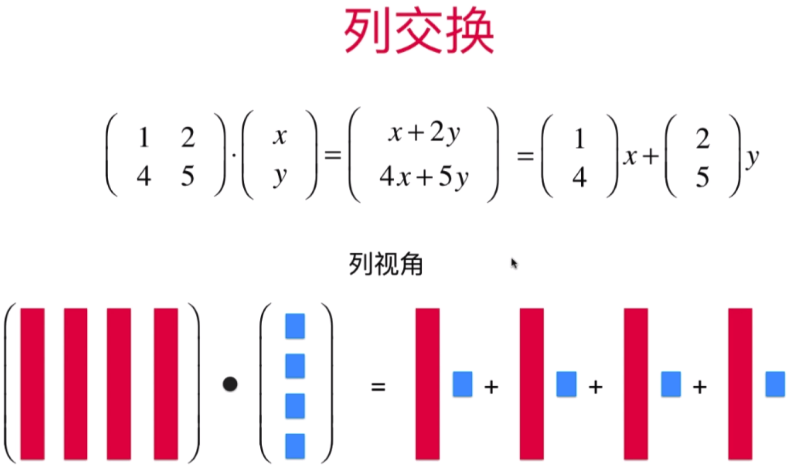
将原矩阵看成分成列乘以置换矩阵中每一列的对应元素进行相加即可
举例:
1 2 3
4 * 1 + 5 * 0 + 6 * 0 这里面的1 0 0 指的是后面单矩阵的列向量,所以第一列为(1 4 7)t 以此计算同理
7 8 9
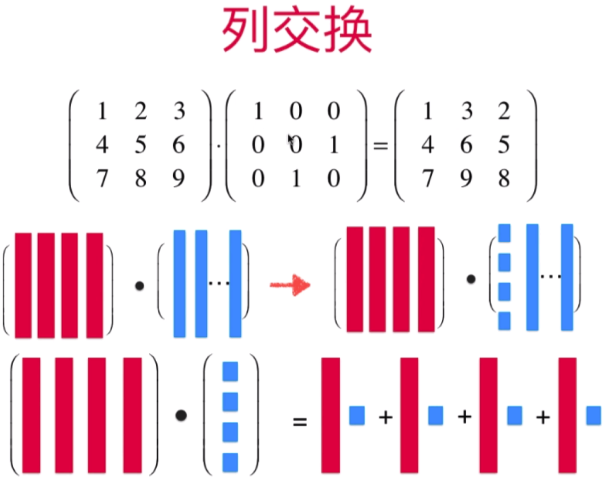
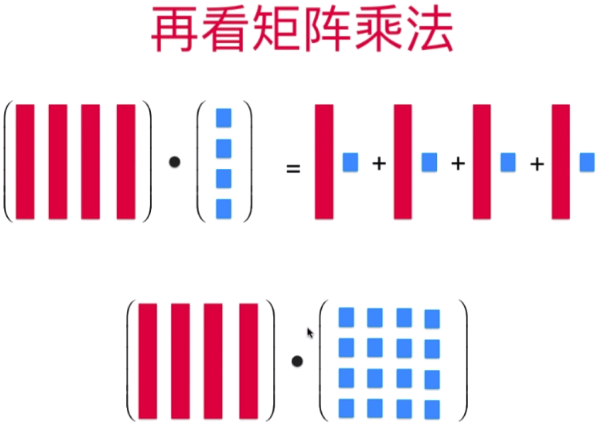
此处为:resij 指的是结果矩阵中的每一个元素的值 (对应行乘以列向量)

列向量乘以行向量得到一个结果矩阵,且结果矩阵中对应行对应列的元素值等于 原矩阵乘以单位矩阵 对应行对应列的元素值
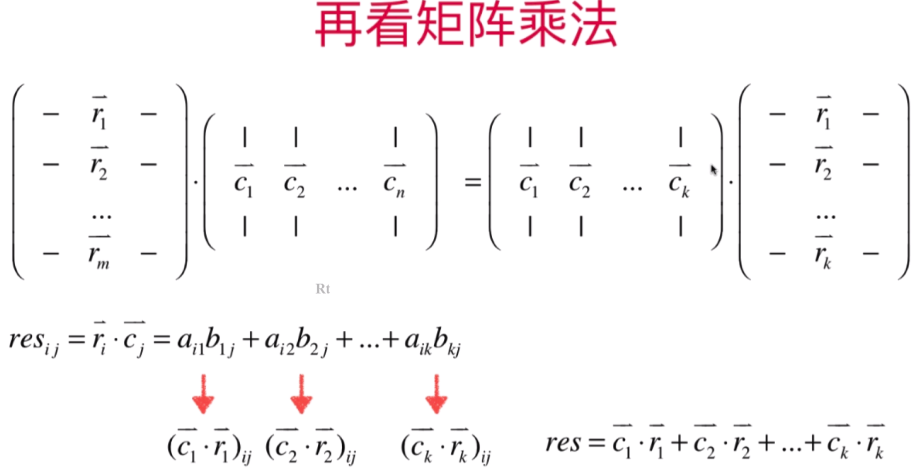
矩阵乘法:
行乘以列: 每一行乘以列点乘得出的元素,此元素为 第几行数等于对应的第几列的
列乘以行: 每一列乘以行点乘得出的矩阵,规则就是列乘以行进行点乘,也遵循行乘以列的点乘规律(矩阵点乘规则)







