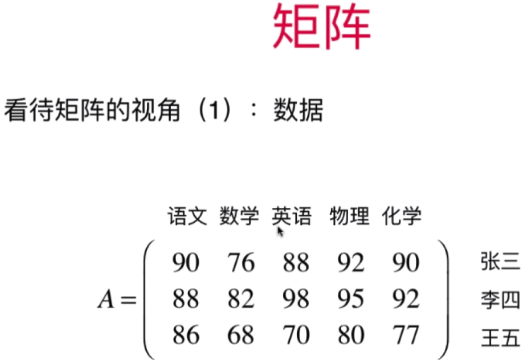
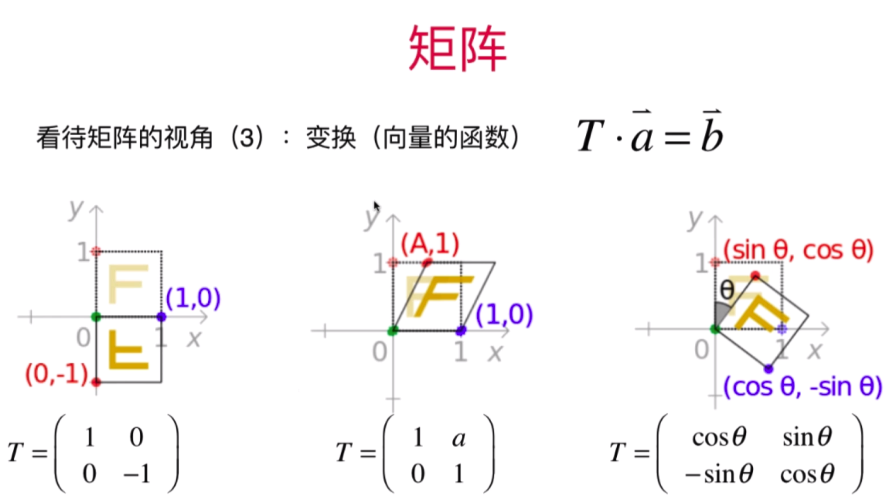
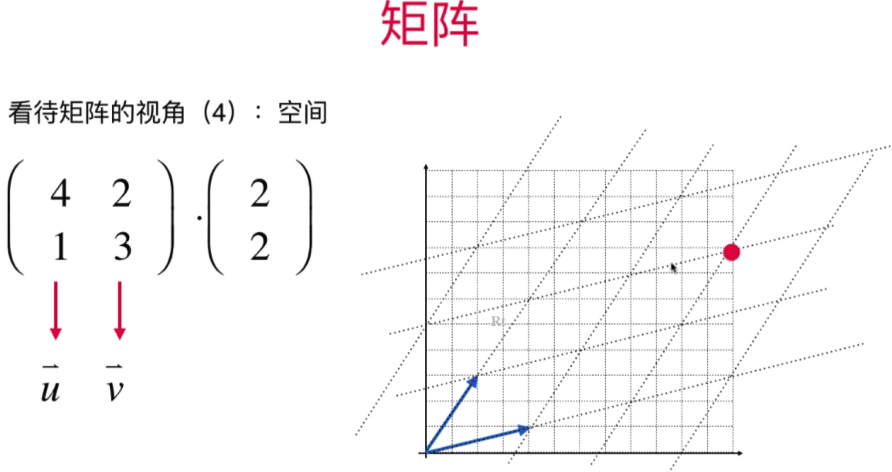
人工智能必备数学知识学习笔记7:矩阵的应用和更多矩阵相关的高级话题

- 更多变换矩阵









- 矩阵旋转变换和矩阵在图形学中的应用
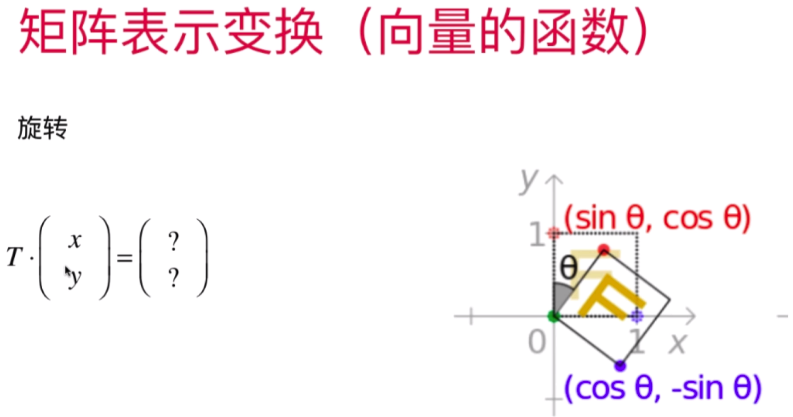
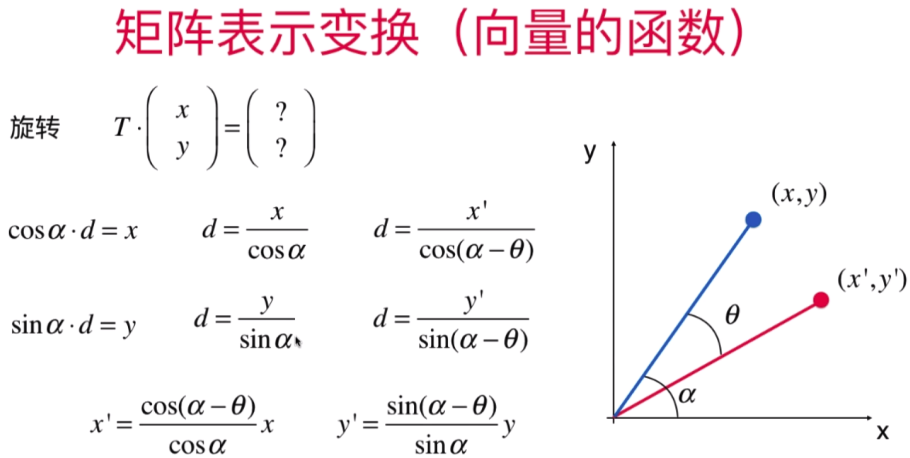
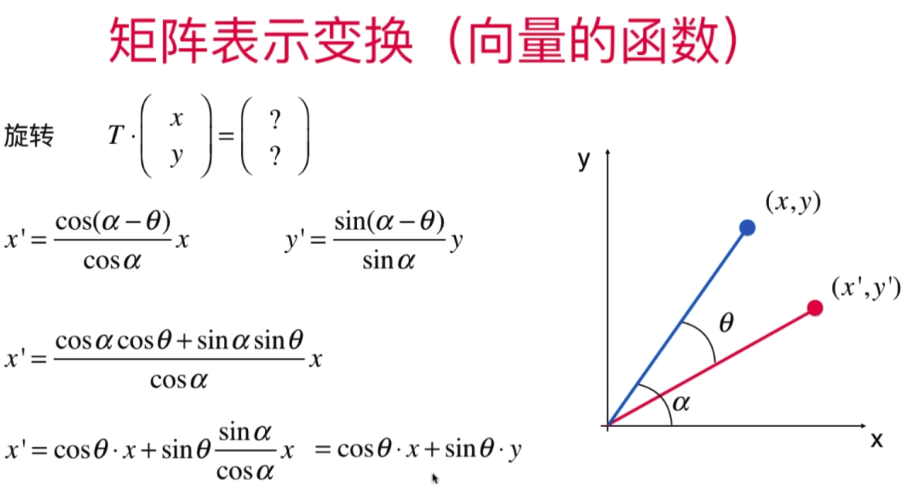
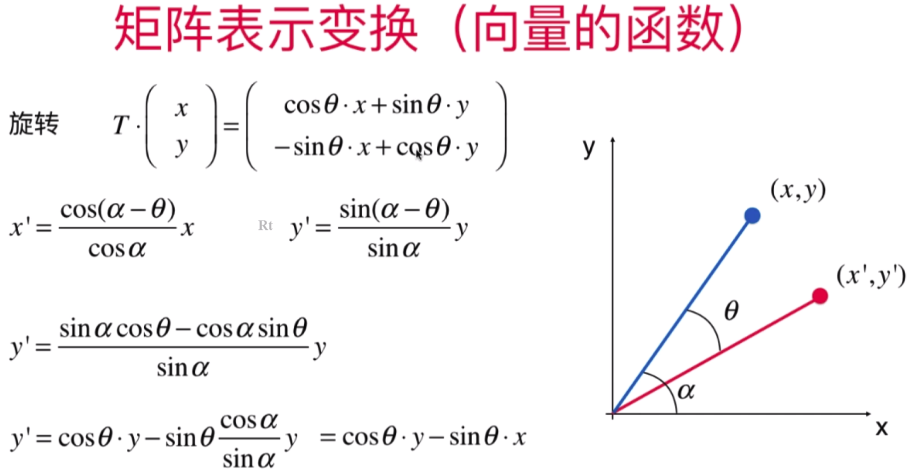
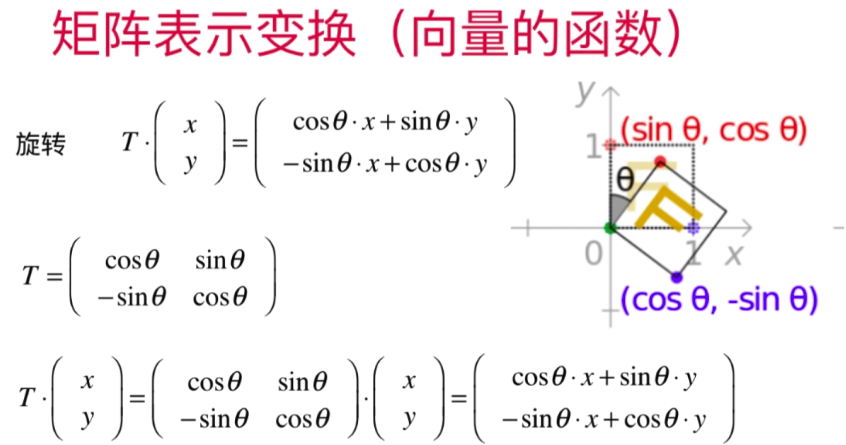

仿射变换:(百度百科 https://baike.baidu.com/item/%E4%BB%BF%E5%B0%84%E5%8F%98%E6%8D%A2/4289056?fr=aladdin)
仿射变换,又称仿射映射,是指在几何中,一个向量空间进行一次线性变换并接上一个平移,变换为另一个向量空间。

图形学:(百度百科:https://baike.baidu.com/item/%E8%AE%A1%E7%AE%97%E6%9C%BA%E5%9B%BE%E5%BD%A2%E5%AD%A6/279486?fr=aladdin)
代码实现:

1.在 main_matrix_transformation.py中编写代码:
1 import matplotlib.pyplot as plt 2 import math 3 from playLA.Matrix import Matrix 4 from playLA.Vector import Vector 5 6 # 绘图数学库 matplotlib 7 if __name__ == "__main__": 8 9 points = [[0,0], [0,5], [3,5], [3,4], [1,4], 10 [1,3], [2,3], [2,2], [1,2], [1,0]] 11 12 x = [point[0] for point in points] 13 y = [point[1] for point in points] 14 15 # 根据点来绘制图案 16 plt.figure(figsize=(5,5))# 设置绘制窗口的大小(单位:英尺) 17 plt.xlim(-10,10)# 设置窗口坐标系x轴的范围 18 plt.ylim(-10,10)# 设置窗口坐标系y轴的范围 19 20 plt.plot(x,y)# 输入绘制点 21 #plt.show()# 窗口展示 22 23 # 将矩阵 P 进行转换 24 P = Matrix(points) 25 26 #T = Matrix([[2,0],[0,1.5]]) # 将矩阵 P 横坐标扩大2倍,纵坐标扩大1.5倍 27 #T = Matrix([[1,0],[0,-1]]) # 将矩阵 P 进行x轴翻转 28 #T = Matrix([[-1,0],[0,1]]) # 将矩阵 P 进行y轴翻转 29 #T = Matrix([[-1, 0], [0, -1]]) # 将矩阵 P 进行原点对称 30 #T = Matrix([[1, 0.5], [0, 1]]) # 将矩阵 P 进行沿着x轴错切操作 31 #T = Matrix([[1, 0], [0.5, 1]]) # 将矩阵 P 进行沿着y轴错切操作 32 33 #旋转操作 34 theta = math.pi / 3 #三分之一π,也就是60度 35 T = Matrix([[math.cos(theta),math.sin(theta)], [-math.sin(theta),math.cos(theta)]]) 36 37 P2 = T.dot(P.T()) # T 点乘已转置后的矩阵P 38 plt.plot([P2.col_vector(i)[0] for i in range(P2.col_num())], 39 [P2.col_vector(j)[1] for j in range(P2.col_num())]) 40 plt.show()
2.运行 main_matrix_transformation.py 结果为:
根据点来绘制图案
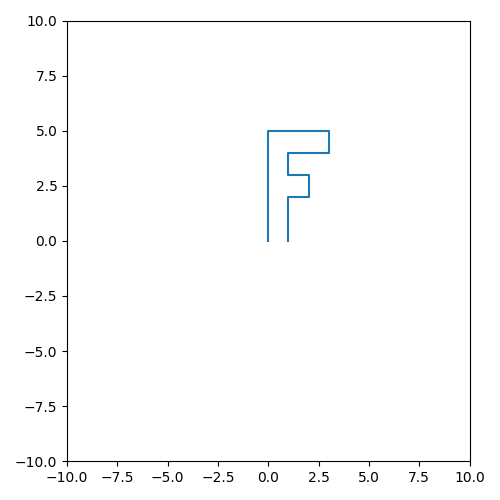
将矩阵 P 横坐标扩大2倍,纵坐标扩大1.5倍
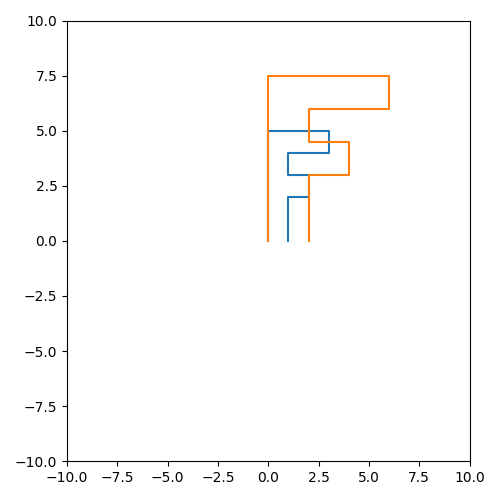
将矩阵 P 进行x轴翻转
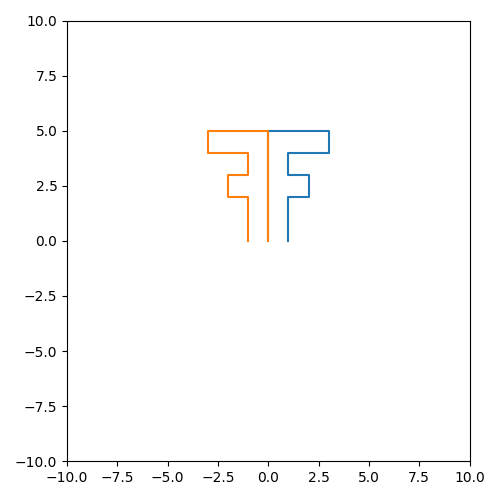
将矩阵 P 进行y轴翻转
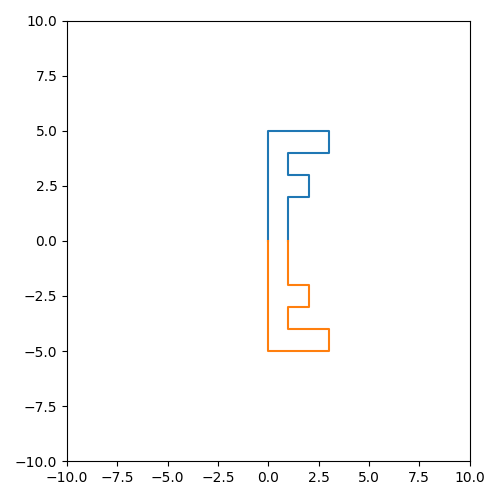 将矩阵 P 进行原点对称
将矩阵 P 进行原点对称
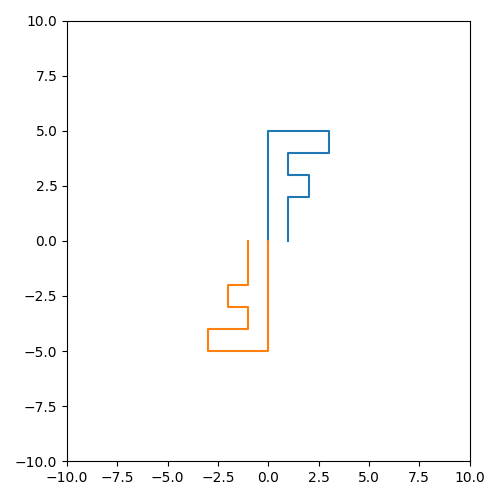
将矩阵 P 进行沿着x轴错切操作
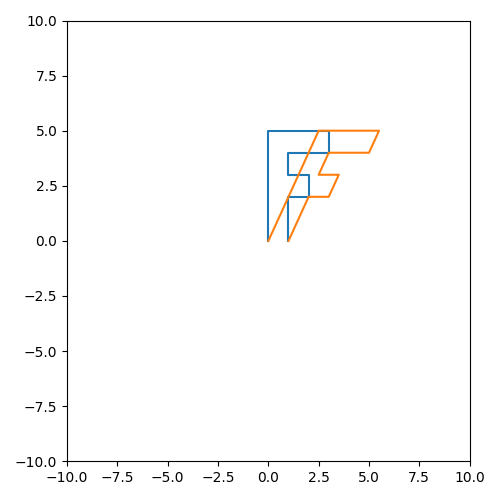 将矩阵 P 进行沿着y轴错切操作
将矩阵 P 进行沿着y轴错切操作
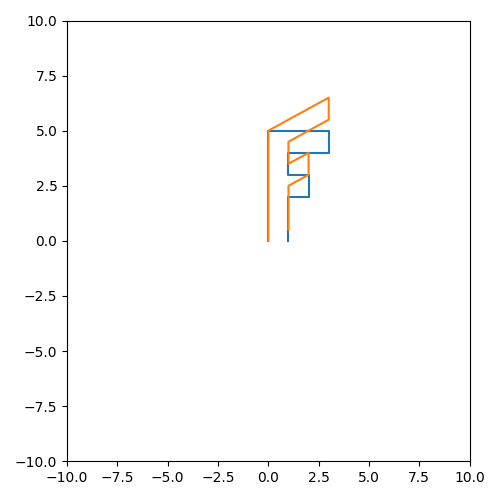
旋转操作:三分之一π,也就是60度
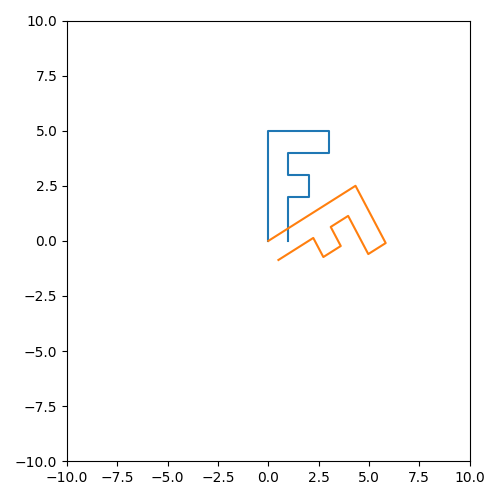
- 从缩放变换到单位矩阵



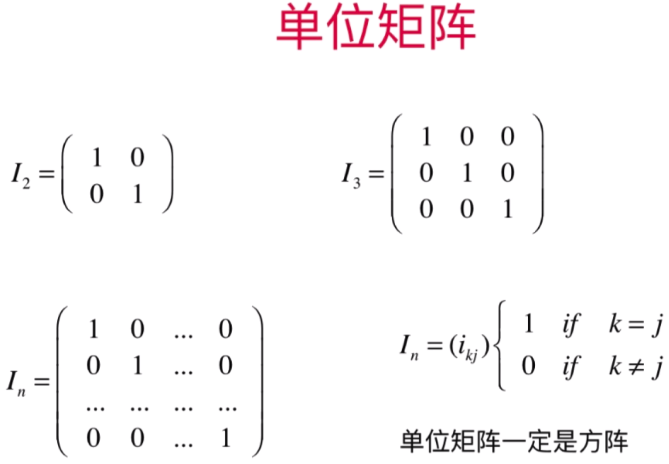
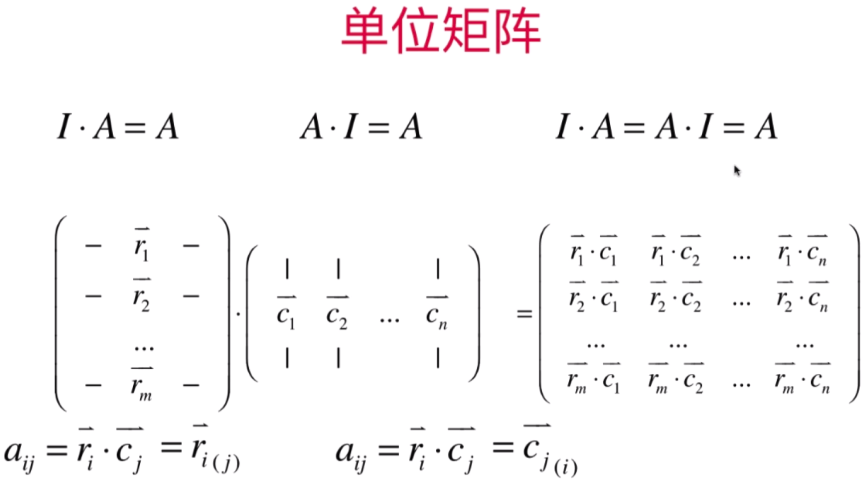

非方形矩阵:需要单位矩阵的列数等于长方形矩阵的行数

- 矩阵的逆






代码实现:
1.在Matrix.py编写代码:单位矩阵类方法:返回一个n行n列的单位矩阵
1 #矩阵类 2 from playLA.Vector import Vector 3 4 5 class Matrix: 6 # 参数2:二维数组 7 def __init__(self, list2d): 8 self._values = [row[:] for row in list2d]#将数组变为矩阵 9 10 #矩阵类方法:返回一个r行c列的零矩阵:参数1:为零的类对象 11 @classmethod 12 def zero(cls,r,c): 13 return cls([[0] * c for _ in range(r)]) #创建一个r行c列为零的一个列表 14 15 #单位矩阵类方法:返回一个n行n列的单位矩阵 16 @classmethod 17 def identity(cls, n): 18 m = [[0] * n for _ in range(n)] #此处 m 代表有 n 行,每一行有 n 个 0 19 for i in range(n): 20 m[i][i] = 1 #此处代表将矩阵 m 的 第i行的第i个元素赋值为1 21 return cls(m) 22 23 #返回矩阵的转置矩阵 24 def T(self): 25 #将每一行的相同位置(每一列)元素提取出来变为行组成新的矩阵 26 return Matrix([[e for e in self.col_vector(i)] 27 for i in range(self.col_num())]) 28 29 #返回两个矩阵的加法结果 30 def __add__(self, another): 31 # 校验两个矩阵的形状为一致(行数、列数一致) 32 assert self.shape() == another.shape(), \ 33 "Error in adding. Shape of matrix must be same." 34 # 根据矩阵的加法公式:两个矩阵对应的每一行的每一个元素相加,获得新的矩阵(遍历两个矩阵对应的每一个行每个元素进行相加<第二步>,外部再遍历该矩阵的行数(循环的次数)<第一步>) 35 return Matrix([[a+b for a,b in zip(self.row_vector(i),another.row_vector(i))] 36 for i in range(self.row_num())]) 37 38 # 返回两个矩阵的减法结果 39 def __sub__(self, another): 40 assert self.shape() == another.shape(), \ 41 "Error in subtracting. Shape of matrix must be same." 42 return Matrix([[a - b for a, b in zip(self.row_vector(i), another.row_vector(i))] 43 for i in range(self.row_num())]) 44 45 #返回两个矩阵的乘法结果(矩阵乘以矩阵) 46 def dot(self,another): 47 if isinstance(another,Vector):#判断是否为向量:矩阵与向量的乘法 48 assert self.col_num() == len(another),\ 49 "Error in Matrix_Vector Multiplication." #矩阵与向量的乘法错误 50 return Vector([self.row_vector(i).dot(another) for i in range(self.row_num())]) 51 if isinstance(another,Matrix):#判断是否为矩阵:矩阵与矩阵的乘法 52 assert self.col_num() == another.row_num(),\ 53 "Error in Matrix-Matrix Multiplication." #矩阵与矩阵的乘法错误 54 # 将矩阵的每一行与另一矩阵的每一列进行向量间的点乘 55 return Matrix([[self.row_vector(i).dot(another.col_vector(j)) for j in range(another.col_num())] 56 for i in range(self.row_num())]) 57 58 #返回矩阵的数量乘结果(矩阵乘以数字):self * k 59 def __mul__(self, k): 60 #通过遍历每一行的每个元素e后分别乘以k<第一步>,外部再遍历该矩阵的行数(循环的次数)<第二步> 61 return Matrix([[e * k for e in self.row_vector(i)] 62 for i in range(self.row_num())]) 63 64 # 返回矩阵的数量乘结果(数字乘以矩阵):k * self 65 def __rmul__(self, k): 66 return self * k 67 68 #返回数量除法的结果矩阵:self / k 69 def __truediv__(self, k): 70 return (1 / k) * self 71 72 #返回矩阵取正的结果 73 def __pos__(self): 74 return 1 * self 75 76 #返回矩阵取负的结果 77 def __neg__(self): 78 return -1 * self 79 80 #返回矩阵的第index个行向量 81 def row_vector(self,index): 82 return Vector(self._values[index]) 83 84 # 返回矩阵的第index个列向量 85 def col_vector(self, index): 86 return Vector([row[index] for row in self._values]) 87 88 #返回矩阵pos位置的元素(根据元素的位置取元素值) :参数2:元组 89 def __getitem__(self, pos): 90 r,c = pos 91 return self._values[r][c] 92 93 #返回矩阵的元素个数 94 def size(self): 95 r,c = self.shape() 96 return r*c 97 98 #返回矩阵行数 99 def row_num(self): 100 return self.shape()[0] 101 102 __len__ = row_num 103 104 #返回矩阵列数 105 def col_num(self): 106 return self.shape()[1] 107 108 #返回矩阵形状:(行数,列数) 109 def shape(self): 110 return len(self._values),len(self._values[0]) 111 112 #矩阵展示 113 def __repr__(self): 114 return "Matrix({})".format(self._values) 115 116 __str__ = __repr__
2.在main-matrix.py编写代码:单位矩阵类方法:返回一个n行n列的单位矩阵
1 from playLA.Matrix import Matrix 2 from playLA.Vector import Vector 3 4 if __name__ == "__main__": 5 #生成一个矩阵 6 matrix = Matrix([[1,2],[3,4]]) 7 print(matrix) 8 #矩阵的行数和列数(返回矩阵形状:(行数,列数)) 9 print("matrix.shape = {}".format(matrix.shape())) 10 #返回矩阵的元素个数 11 print("matrix.size = {}".format(matrix.size())) 12 print("len(matrix) = {}".format(len(matrix))) 13 #根据元素的位置取元素值 14 print("matrix[0][0] = {}".format(matrix[0,0])) 15 # 返回矩阵的第index个行向量 16 print("matrix.row_vector = {}".format(matrix.row_vector(0))) 17 # 返回矩阵的第index个列向量 18 print("matrix.col_vector = {}".format(matrix.col_vector(0))) 19 20 # 返回两个矩阵的加法结果 21 matrix2 = Matrix([[5,6],[7,8]]) 22 print("add:{}".format(matrix + matrix2)) 23 # 返回两个矩阵的减法结果 24 print("subtract:{}".format(matrix - matrix2)) 25 #返回矩阵的数量乘结果(矩阵乘以数字):self * k 26 print("scalar-mul:{}".format(matrix * 2)) 27 # 返回矩阵的数量乘结果(数字乘以矩阵):k * self 28 print("scalar-mul:{}".format(2 * matrix)) 29 # 零矩阵类方法:返回一个2行3列的零矩阵 30 print("zero_2_3:{}".format(Matrix.zero(2,3))) 31 32 # 返回两个矩阵的乘法结果(矩阵乘以矩阵) 33 T = Matrix([[1.5,0],[0,2]]) 34 p = Vector([5,3]) 35 print("T.dot(p) = {}".format(T.dot(p))) 36 P = Matrix([[0,4,5],[0,0,3]]) 37 print("T.dot(P) = {}".format(T.dot(P))) 38 print("matrix.dot(matrix2) = {}".format(matrix.dot(matrix2))) 39 print("matrix2.dot(matrix) = {}".format(matrix2.dot(matrix))) 40 41 # 返回矩阵的转置矩阵 42 print("P.T = {}".format(P.T())) 43 44 #单位矩阵类方法:返回一个n行n列的单位矩阵 45 I = Matrix.identity(2) 46 print(I) 47 print("A.dot(I) = {}".format(matrix.dot(I))) 48 print("I.dot(A) = {}".format(I.dot(matrix)))
3.运行main_matrix.py结果为:
1 /Users/liuxiaoming/PycharmProjects/LinearAlgebra/venv/bin/python /Applications/PyCharm.app/Contents/plugins/python/helpers/pydev/pydevconsole.py --mode=client --port=52708 2 import sys; print('Python %s on %s' % (sys.version, sys.platform)) 3 sys.path.extend(['/Users/liuxiaoming/PycharmProjects/LinearAlgebra']) 4 PyDev console: starting. 5 Python 3.8.2 (v3.8.2:7b3ab5921f, Feb 24 2020, 17:52:18) 6 [Clang 6.0 (clang-600.0.57)] on darwin 7 >>> runfile('/Users/liuxiaoming/PycharmProjects/LinearAlgebra/main_matrix.py', wdir='/Users/liuxiaoming/PycharmProjects/LinearAlgebra') 8 Matrix([[1, 2], [3, 4]]) 9 matrix.shape = (2, 2) 10 matrix.size = 4 11 len(matrix) = 2 12 matrix[0][0] = 1 13 matrix.row_vector = (1, 2) 14 matrix.col_vector = (1, 3) 15 add:Matrix([[6, 8], [10, 12]]) 16 subtract:Matrix([[-4, -4], [-4, -4]]) 17 scalar-mul:Matrix([[2, 4], [6, 8]]) 18 scalar-mul:Matrix([[2, 4], [6, 8]]) 19 zero_2_3:Matrix([[0, 0, 0], [0, 0, 0]]) 20 T.dot(p) = (7.5, 6) 21 T.dot(P) = Matrix([[0.0, 6.0, 7.5], [0, 0, 6]]) 22 matrix.dot(matrix2) = Matrix([[19, 22], [43, 50]]) 23 matrix2.dot(matrix) = Matrix([[23, 34], [31, 46]]) 24 P.T = Matrix([[0, 0], [4, 0], [5, 3]]) 25 Matrix([[1, 0], [0, 1]]) 26 A.dot(I) = Matrix([[1, 2], [3, 4]]) 27 I.dot(A) = Matrix([[1, 2], [3, 4]])
4. (矩阵再numpy中的应用)文件 main_numpy_vector.py 编写代码:单位矩阵、逆矩阵
1 import numpy as np 2 3 if __name__ == "__main__": 4 5 #矩阵的创建 6 A =np.array([[1,2],[3,4]]) 7 print(A) 8 9 #矩阵的属性 10 print(A.shape)#矩阵的形状(行数、列数) 11 print(A.T)#矩阵的转置 12 13 #获取矩阵的元素(从零开始计算) 14 print(A[1,1])#矩阵的某个元素 15 print(A[0])#矩阵的行向量 等价于 A([0,:]) 16 print(A[:,0])#矩阵的列向量(两个索引:索引1:冒号取全部行,索引2:某一列) 17 18 #矩阵的基本运算 19 B = np.array([[5,6],[7,8]]) 20 print("A + B = {}".format(A + B)) 21 print("A - b = {}".format(A - B)) 22 print("10 * A = {}".format(10 * A)) 23 print("A * 10 = {}".format(A * 10)) 24 print(A * B)#矩阵中每个元素对应元素相乘而已(不是线性代数中的矩阵相乘) 25 print("A.dot(B) = {}".format(A.dot(B)))#矩阵之间相乘 26 27 p = np.array([10,100]) 28 print("A + p = {}".format(A + p))#此处处理为广播机制处理,也就是每一行对应的每个元素进行相加,但不是线性代数中的矩阵加法 29 print("A + 1 = {}".format(A + 1))#此处处理为广播机制处理,也就是每一行对应的每个元素进行相加,但不是线性代数中的矩阵加法 30 31 print("A.dot(p) = {}".format(A.dot(p)))#矩阵乘以向量 32 33 # 单位矩阵 34 I = np.identity(2) 35 print(I) 36 print("A.dot(I) = {}".format(A.dot(I))) 37 print("I.dot(A) = {}".format(I.dot(A))) 38 39 #逆矩阵 40 invA = np.linalg.inv(A) 41 print(invA) 42 print(invA.dot(A)) 43 print(A.dot(invA)) 44 45 # 只有方阵才会有逆矩阵:对于非方阵取逆矩阵时会报错 46 C = np.array([[1,2,3],[4,5,6]]) 47 np.linalg.inv(C)
5. 运行文件 main_numpy_vector.py 结果为:
1 /Users/liuxiaoming/PycharmProjects/LinearAlgebra/venv/bin/python /Users/liuxiaoming/PycharmProjects/LinearAlgebra/playLA/main_numpy_matrix.py 2 [[1 2] 3 [3 4]] 4 (2, 2) 5 [[1 3] 6 [2 4]] 7 4 8 [1 2] 9 [1 3] 10 A + B = [[ 6 8] 11 [10 12]] 12 A - b = [[-4 -4] 13 [-4 -4]] 14 10 * A = [[10 20] 15 [30 40]] 16 A * 10 = [[10 20] 17 [30 40]] 18 [[ 5 12] 19 [21 32]] 20 A.dot(B) = [[19 22] 21 [43 50]] 22 A + p = [[ 11 102] 23 [ 13 104]] 24 A + 1 = [[2 3] 25 [4 5]] 26 A.dot(p) = [210 430] 27 [[1. 0.] 28 [0. 1.]] 29 A.dot(I) = [[1. 2.] 30 [3. 4.]] 31 I.dot(A) = [[1. 2.] 32 [3. 4.]] 33 [[-2. 1. ] 34 [ 1.5 -0.5]] 35 [[1.00000000e+00 0.00000000e+00] 36 [1.11022302e-16 1.00000000e+00]] 37 [[1.0000000e+00 0.0000000e+00] 38 [8.8817842e-16 1.0000000e+00]] 39 Traceback (most recent call last): 40 File "/Users/liuxiaoming/PycharmProjects/LinearAlgebra/playLA/main_numpy_matrix.py", line 47, in <module> 41 np.linalg.inv(C) 42 File "<__array_function__ internals>", line 5, in inv 43 File "/Users/liuxiaoming/PycharmProjects/LinearAlgebra/venv/lib/python3.8/site-packages/numpy/linalg/linalg.py", line 541, in inv 44 _assert_stacked_square(a) 45 File "/Users/liuxiaoming/PycharmProjects/LinearAlgebra/venv/lib/python3.8/site-packages/numpy/linalg/linalg.py", line 204, in _assert_stacked_square 46 raise LinAlgError('Last 2 dimensions of the array must be square') 47 numpy.linalg.LinAlgError: Last 2 dimensions of the array must be square 48 49 Process finished with exit code 1
- 矩阵的逆的性质






- 看待矩阵的关键视角:用矩阵表示空间


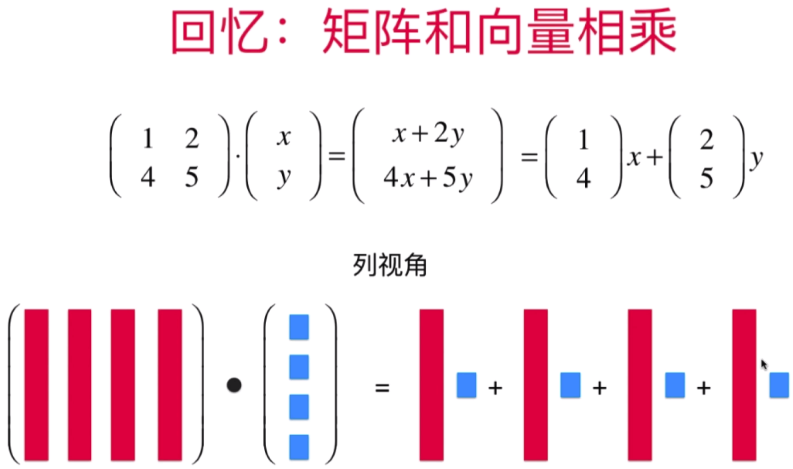


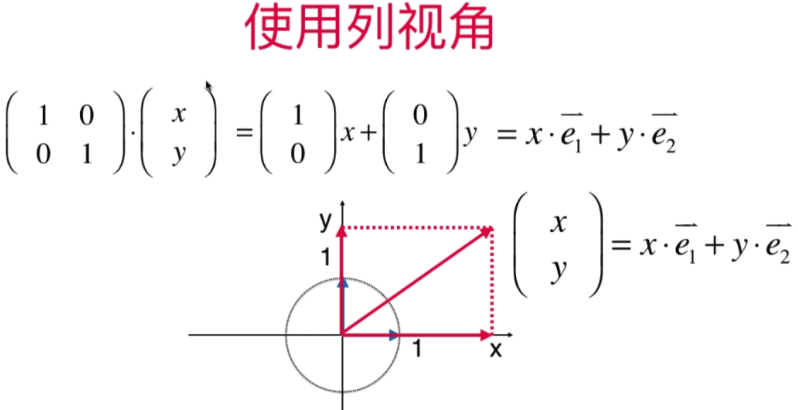
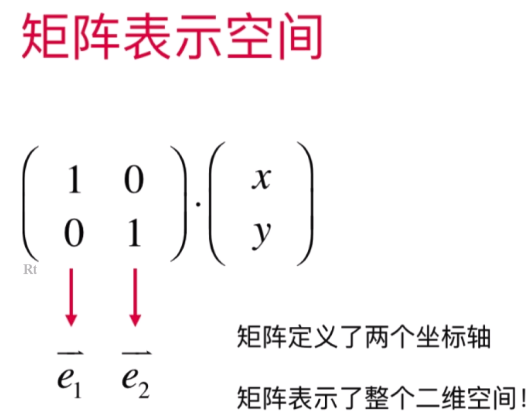
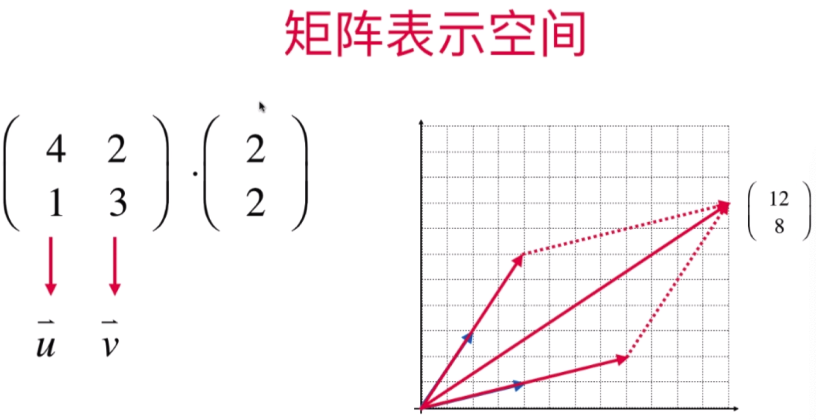
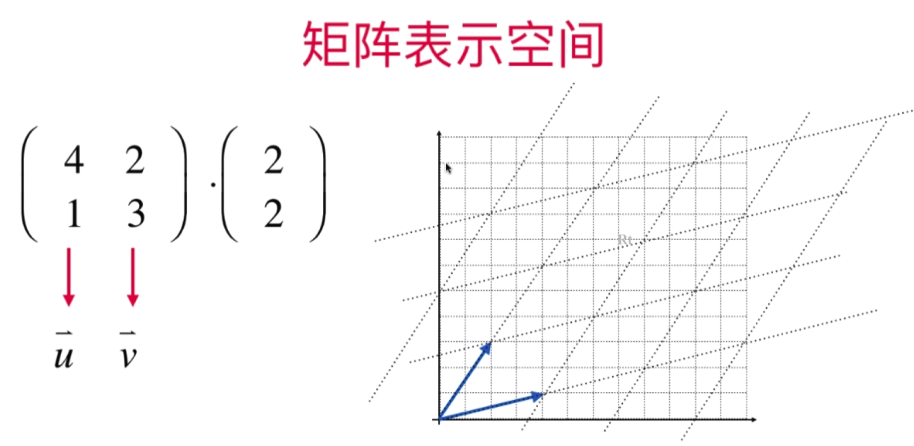
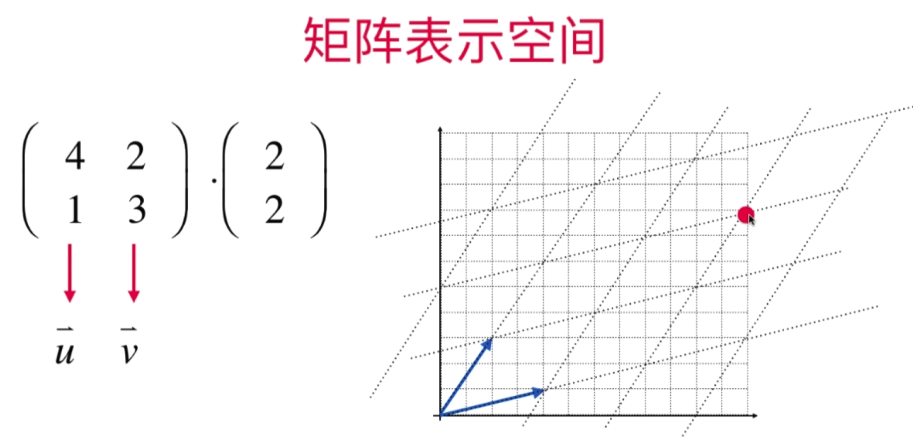
将原矩阵图形放入一个新的矩阵空间(T)中展示的样子:
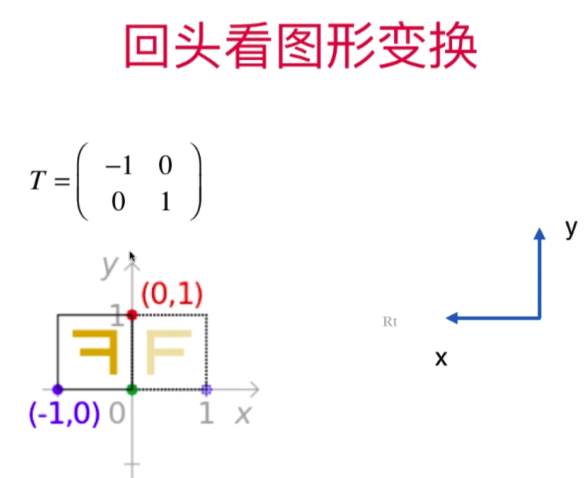
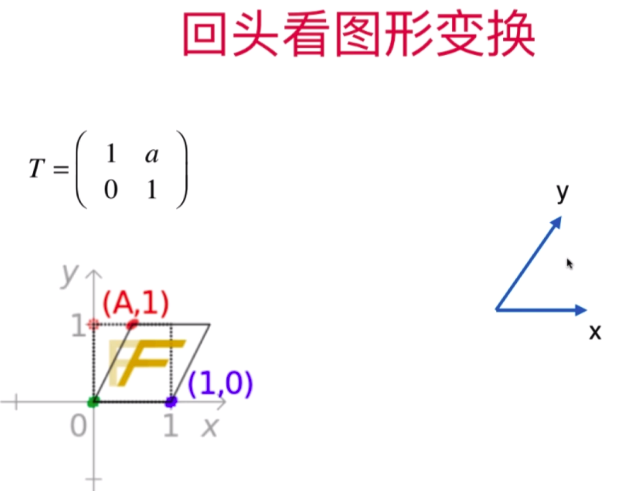


- 总结:看待矩阵的四个重要视角