文本相似性计算--MinHash和LSH算法
给定N个集合,从中找到相似的集合对,如何实现呢?直观的方法是比较任意两个集合。那么可以十分精确的找到每一对相似的集合,但是时间复杂度是O(n2)。此外,假如,N个集合中只有少数几对集合相似,绝大多数集合都不相似,该方法在两两比较过程中“浪费了计算时间”。所以,如果能找到一种算法,将大体上相似的集合聚到一起,缩小比对的范围,这样只用检测较少的集合对,就可以找到绝大多数相似的集合对,大幅度减少时间开销。虽然牺牲了一部分精度,但是如果能够将时间大幅度减少,这种算法还是可以接受的。接下来的内容讲解如何使用Minhash和LSH(Locality-sensitive Hashing)来实现上述目的,在相似的集合较少的情况下,可以在O(n)时间找到大部分相似的集合对。
一、Jaccard相似度
判断两个集合是否相等,一般使用称之为Jaccard相似度的算法(后面用Jac(S1,S2)来表示集合S1和S2的Jaccard相似度)。举个列子,集合X = {a,b,c},Y = {b,c,d}。那么Jac(X,Y) = 2 / 4 = 0.50。也就是说,结合X和Y有50%的元素相同。下面是形式的表述Jaccard相似度公式:
Jac(X,Y) = |X∩Y| / |X∪Y|
也就是两个结合交集的个数比上两个集合并集的个数。范围在[0,1]之间。
二、降维技术Minhash
原始问题的关键在于计算时间太长。如果能够找到一种很好的方法将原始集合压缩成更小的集合,而且又不失去相似性,那么可以缩短计算时间。Minhash可以帮助我们解决这个问题。举个例子,S1 = {a,d,e},S2 = {c, e},设全集U = {a,b,c,d,e}。集合可以如下表示:
|
行号 |
元素 |
S1 |
S2 |
类别 |
|
1 |
a |
1 |
0 |
Y |
|
2 |
b |
0 |
0 |
Z |
|
3 |
c |
0 |
1 |
Y |
|
4 |
d |
1 |
0 |
Y |
|
5 |
e |
1 |
1 |
X |
表1
表1中,列表示集合,行表示元素,值1表示某个集合具有某个值,0则相反(X,Y,Z的意义后面讨论)。Minhash算法大体思路是:采用一种hash函数,将元素的位置均匀打乱,然后将新顺序下每个集合第一个元素作为该集合的特征值。比如哈希函数h1(i) = (i + 1) % 5,其中i为行号。作用于集合S1和S2,得到如下结果:
|
行号 |
元素 |
S1 |
S2 |
类别 |
|
1 |
e |
1 |
1 |
X |
|
2 |
a |
1 |
0 |
Y |
|
3 |
b |
0 |
0 |
Z |
|
4 |
c |
0 |
1 |
Y |
|
5 |
d |
1 |
0 |
Y |
|
Minhash |
e |
e |
|
|
表2
这时,Minhash(S1) = e,Minhash(S2) = e。也就是说用元素e表示S1,用元素e表示集合S2。那么这样做是否科学呢?进一步,如果Minhash(S1) 等于Minhash(S2),那么S1是否和S2类似呢?
MinHash的合理性分析
首先给出结论,在哈希函数h1均匀分布的情况下,集合S1的Minhash值和集合S2的Minhash值相等的概率等于集合S1与集合S2的Jaccard相似度,即:
P(Minhash(S1) = Minhash(S2)) = Jac(S1,S2)
下面简单分析一下这个结论。
S1和S2的每一行元素可以分为三类:
X类 均为1。比如表2中的第1行,两个集合都有元素e。
Y类 一个为1,另一个为0。比如表2中的第2行,表明S1有元素a,而S2没有。
Z类 均为0。比如表2中的第3行,两个集合都没有元素b。
这里忽略所有Z类的行,因为此类行对两个集合是否相似没有任何贡献。由于哈希函数将原始行号均匀分布到新的行号,这样可以认为在新的行号排列下,任意一行出现X类的情况的概率为|X|/(|X|+|Y|)。这里为了方便,将任意位置设为第一个出现X类行的行号。所以P(第一个出现X类) = |X|/(|X|+|Y|) = Jac(S1,S2)。这里很重要的一点就是要保证哈希函数可以将数值均匀分布,尽量减少冲撞。
一般而言,会找出一系列的哈希函数,比如h个(h << |U|),为每一个集合计算h次Minhash值,然后用h个Minhash值组成一个摘要来表示当前集合(注意Minhash的值的位置需要保持一致)。举个列子,还是基于上面的例子,现在又有一个哈希函数h2(i) = (i -1)% 5。那么得到如下集合:
|
行号 |
元素 |
S1 |
S2 |
类别 |
|
1 |
b |
0 |
0 |
Z |
|
2 |
c |
0 |
1 |
Y |
|
3 |
d |
1 |
0 |
Y |
|
4 |
e |
1 |
1 |
X |
|
5 |
a |
1 |
0 |
Y |
|
Minhash |
d |
c |
|
|
表3
所以,现在用摘要表示的原始集合如下:
|
哈希函数 |
S1 |
S2 |
|
h1(i) = (i + 1) % 5 |
e |
e |
|
h2(i) = (i - 1) % 5 |
d |
c |
表4
从表四还可以得到一个结论,令X表示Minhash摘要后的集合对应行相等的次数(比如表4,X=1,因为哈希函数h1情况下,两个集合的minhash相等,h2不等):
X ~ B(h,Jac(S1,S2))
X符合次数为h,概率为Jac(S1,S2)的二项分布。那么期望E(X) = h * Jac(S1,S2) = 2 * 2 / 3 = 1.33。也就是每2个hash计算Minhash摘要,可以期望有1.33元素对应相等。所以,Minhash在压缩原始集合的情况下,保证了集合的相似度没有被破坏。
三、LSH – 局部敏感哈希
现在有了原始集合的摘要,但是还是没有解决最初的问题,仍然需要遍历所有的集合对,才能所有相似的集合对,复杂度仍然是O(n2)。所以,接下来描述解决这个问题的核心思想LSH。其基本思路是将相似的集合聚集到一起,减小查找范围,避免比较不相似的集合。仍然是从例子开始,现在有5个集合,计算出对应的Minhash摘要,如下:
|
|
S1 |
S2 |
S3 |
S4 |
S5 |
|
区间1 |
b |
b |
a |
b |
a |
|
c |
c |
a |
c |
b |
|
|
d |
b |
a |
d |
c |
|
|
区间2 |
a |
e |
b |
e |
d |
|
b |
d |
c |
f |
e |
|
|
e |
a |
d |
g |
a |
|
|
区间3 |
d |
c |
a |
h |
b |
|
a |
a |
b |
b |
a |
|
|
d |
e |
a |
b |
e |
|
|
区间4 |
d |
a |
a |
c |
b |
|
b |
a |
c |
b |
a |
|
|
d |
e |
a |
b |
e |
表5
上面的集合摘要采用了12个不同的hash函数计算出来,然后分成了B = 4个区间。前面已经分析过,任意两个集合(S1,S2)对应的Minhash值相等的概率r = Jac(S1,S2)。先分析区间1,在这个区间内,P(集合S1等于集合S2) = r3。所以只要S1和S2的Jaccard相似度越高,在区间1内越有可能完成全一致,反过来也一样。那么P(集合S1不等于集合S2) = 1 - r3。现在有4个区间,其他区间与第一个相同,所以P(4个区间上,集合S1都不等于集合S2) = (1 – r3)4。P(4个区间上,至少有一个区间,集合S1等于集合S2) = 1 - (1 – r3)4。这里的概率是一个r的函数,形状犹如一个S型,如下:
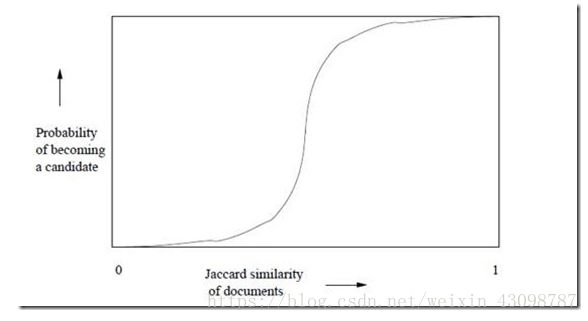
图1
如果令区间个数为B,每个区间内的行数为C,那么上面的公式可以形式的表示为:
P(B个区间中至少有一个区间中两个结合相等) = 1 - (1 – rC)B
令r = 0.4,C=3,B = 100。上述公式计算的概率为0.9986585。这表明两个Jaccard相似度为0.4的集合在至少一个区间内冲撞的概率达到了99.9%。根据这一事实,我们只需要选取合适的B和C,和一个冲撞率很低的hash函数,就可以将相似的集合至少在一个区间内冲撞,这样也就达成了本节最开始的目的:将相似的集合放到一起。具体的方法是为B个区间,准备B个hash表,和区间编号一一对应,然后用hash函数将每个区间的部分集合映射到对应hash表里。最后遍历所有的hash表,将冲撞的集合作为候选对象进行比较,找出相识的集合对。整个过程是采用O(n)的时间复杂度,因为B和C均是常量。由于聚到一起的集合相比于整体比较少,所以在这小范围内互相比较的时间开销也可以计算为常量,那么总体的计算时间也是O(n)。
四、代码实现
方法一:引用python包datasketch
安装:
pip install datasketch
使用示例如下:
MinHash
from datasketch import MinHash data1 = ['minhash', 'is', 'a', 'probabilistic', 'data', 'structure', 'for', 'estimating', 'the', 'similarity', 'between', 'datasets'] data2 = ['minhash', 'is', 'a', 'probability', 'data', 'structure', 'for', 'estimating', 'the', 'similarity', 'between', 'documents'] m1, m2 = MinHash(), MinHash() for d in data1: m1.update(d.encode('utf8')) for d in data2: m2.update(d.encode('utf8')) print("Estimated Jaccard for data1 and data2 is", m1.jaccard(m2)) s1 = set(data1) s2 = set(data2) actual_jaccard = float(len(s1.intersection(s2)))/float(len(s1.union(s2))) print("Actual Jaccard for data1 and data2 is", actual_jaccard)
MinHash LSH
from datasketch import MinHash, MinHashLSH set1 = set(['minhash', 'is', 'a', 'probabilistic', 'data', 'structure', 'for', 'estimating', 'the', 'similarity', 'between', 'datasets']) set2 = set(['minhash', 'is', 'a', 'probability', 'data', 'structure', 'for', 'estimating', 'the', 'similarity', 'between', 'documents']) set3 = set(['minhash', 'is', 'probability', 'data', 'structure', 'for', 'estimating', 'the', 'similarity', 'between', 'documents']) m1 = MinHash(num_perm=128) m2 = MinHash(num_perm=128) m3 = MinHash(num_perm=128) for d in set1: m1.update(d.encode('utf8')) for d in set2: m2.update(d.encode('utf8')) for d in set3: m3.update(d.encode('utf8')) # Create LSH index lsh = MinHashLSH(threshold=0.5, num_perm=128) lsh.insert("m2", m2) lsh.insert("m3", m3) result = lsh.query(m1) print("Approximate neighbours with Jaccard similarity > 0.5", result)
MinHash LSH Forest——局部敏感随机投影森林
from datasketch import MinHashLSHForest, MinHash data1 = ['minhash', 'is', 'a', 'probabilistic', 'data', 'structure', 'for', 'estimating', 'the', 'similarity', 'between', 'datasets'] data2 = ['minhash', 'is', 'a', 'probability', 'data', 'structure', 'for', 'estimating', 'the', 'similarity', 'between', 'documents'] data3 = ['minhash', 'is', 'probability', 'data', 'structure', 'for', 'estimating', 'the', 'similarity', 'between', 'documents'] # Create MinHash objects m1 = MinHash(num_perm=128) m2 = MinHash(num_perm=128) m3 = MinHash(num_perm=128) for d in data1: m1.update(d.encode('utf8')) for d in data2: m2.update(d.encode('utf8')) for d in data3: m3.update(d.encode('utf8')) # Create a MinHash LSH Forest with the same num_perm parameter forest = MinHashLSHForest(num_perm=128) # Add m2 and m3 into the index forest.add("m2", m2) forest.add("m3", m3) # IMPORTANT: must call index() otherwise the keys won't be searchable forest.index() # Check for membership using the key print("m2" in forest) print("m3" in forest) # Using m1 as the query, retrieve top 2 keys that have the higest Jaccard result = forest.query(m1, 2) print("Top 2 candidates", result)
方法二minHash源码实现如下:
from random import randint, seed, choice, random import string import sys import itertools def generate_random_docs(n_docs, max_doc_length, n_similar_docs): for i in range(n_docs): if n_similar_docs > 0 and i % 10 == 0 and i > 0: permuted_doc = list(lastDoc) permuted_doc[randint(0,len(permuted_doc))] = choice('1234567890') n_similar_docs -= 1 yield ''.join(permuted_doc) else: lastDoc = ''.join(choice('aaeioutgrb ') for _ in range(randint(int(max_doc_length*.75), max_doc_length))) yield lastDoc def generate_shingles(doc, shingle_size): shingles = set([]) for i in range(len(doc)-shingle_size+1): shingles.add(doc[i:i+shingle_size]) return shingles def get_minhash(shingles, n_hashes, random_strings): minhash_row = [] for i in range(n_hashes): minhash = sys.maxsize for shingle in shingles: hash_candidate = abs(hash(shingle + random_strings[i])) if hash_candidate < minhash: minhash = hash_candidate minhash_row.append(minhash) return minhash_row def get_band_hashes(minhash_row, band_size): band_hashes = [] for i in range(len(minhash_row)): if i % band_size == 0: if i > 0: band_hashes.append(band_hash) band_hash = 0 band_hash += hash(minhash_row[i]) return band_hashes def get_similar_docs(docs, n_hashes=400, band_size=7, shingle_size=3, collectIndexes=True): hash_bands = {} random_strings = [str(random()) for _ in range(n_hashes)] docNum = 0 for doc in docs: shingles = generate_shingles(doc, shingle_size) minhash_row = get_minhash(shingles, n_hashes, random_strings) band_hashes = get_band_hashes(minhash_row, band_size) docMember = docNum if collectIndexes else doc for i in range(len(band_hashes)): if i not in hash_bands: hash_bands[i] = {} if band_hashes[i] not in hash_bands[i]: hash_bands[i][band_hashes[i]] = [docMember] else: hash_bands[i][band_hashes[i]].append(docMember) docNum += 1 similar_docs = set() for i in hash_bands: for hash_num in hash_bands[i]: if len(hash_bands[i][hash_num]) > 1: for pair in itertools.combinations(hash_bands[i][hash_num], r=2): similar_docs.add(pair) return similar_docs if __name__ == '__main__': n_hashes = 200 band_size = 7 shingle_size = 3 n_docs = 1000 max_doc_length = 40 n_similar_docs = 10 seed(42) docs = generate_random_docs(n_docs, max_doc_length, n_similar_docs) similar_docs = get_similar_docs(docs, n_hashes, band_size, shingle_size, collectIndexes=False) print(similar_docs) r = float(n_hashes/band_size) similarity = (1/r)**(1/float(band_size)) print("similarity: %f" % similarity) print("# Similar Pairs: %d" % len(similar_docs)) if len(similar_docs) == n_similar_docs: print("Test Passed: All similar pairs found.") else: print("Test Failed.")
参考:
https://www.cnblogs.com/bourneli/archive/2013/04/04/2999767.html
https://blog.csdn.net/weixin_43098787/article/details/82838929



