分类性能指标
一直以来,被召回率准确率精准率查全率查准率F1值混淆矩阵aucrocTPNPTNPN等等等等所困惑,每次需要知道具体的含义,都是去百度,百度完了看了就忘了,生气!百度了几十遍了!这回一定要总结完毕!
一、从混淆矩阵说起
|
混淆矩阵 confusion matrix |
我预测的 | |||
| 正类 | 负类 | |||
| 实际情况 | 正类 | TP | FN | TP+FN=实际正样本数 |
| 负类 | FP | TN | FP+TN=实际负样本数 | |
| TP+FP=我预测的正样本数 | FN+TN=我预测的负样本数 | |||
图1 混淆矩阵
❤对于四个格子中的TPFNFPTN可以分成两部分来看:
首字母T/N:表示一种判断,即这种判断是True or False。例如TP,是把正类预测成正类,这个判断是对的,所以是T;例如TN,是把负类预测成负类,也是对的,所以T。
尾字母P/N:表示预测的结果,即预测成Positive or Negative。例如FN,预测结果就是负类N;FP,预测结果是正类P。
继续看混淆矩阵,我们可以知道正对角线上的两个值:TP TN,越大越好,因为这是两个代表判断正确的值,最好的结果就是正对角线上值最大,副对角线上值为0。
❤那么对于TP+FN,FP+TN,TP+FP,FN+TN要怎么快速反映出它代表的是什么呢?以前我总是慢慢推,但现在看来也有规律:
首先看首字母,首字母一定是一个T一个F;
然后看尾字母,如果尾字母不相同,那么就大胆的判断一定是实际情况,否则就是预测情况。例如我可以很快看出TP+FN一定是实际的某类样本数,而TP+FP一定不是实际情况。
既然这个加法算式的首字母一定是一个T一个F,那么我们就继续看T的后面,如果T后是P,那么就是正样本数,如果T后是N就是负样本数。
现在做个例题吧!TP+FN,由于字母没有重合,所以这是实际样本数;因为T后面是P,所以是正样本;总结起来就是TP+FN代表着实际情况中正样本的数量。
二、几个指标
有了TP TN FP FN之后,就可以慢慢推出其他指标,先理性的认识一下,就是看看公式:
❤精准率(Precision)=TP/(TP+FP) #又叫查准率,针对预测结果(预测全为正的样本)而言,预测结果中有多少是对的。网上的说法都是“预测的结果有多少是正类”,其实这个正类个人感觉有歧义。
❤召回率(Recall)=TP/(TP+FN) #又叫查全率,针对实际结果而言,预测结果有多少是对的。
可以看到,二者分母相同,都是TP,对应在上述混淆矩阵中就是把正类预测成正类,但如果狭义的去理解这个正类,有可能在做实验的时候陷入迷茫。先明确,每个类别其实都有它的Precision和Recall,负类也有,只是负类的精准率=TN/TN+FN,召回率=TN/TN+FP。而我们日常说的用来衡量模型好坏的标准之二精确率和召回率都针对正类(标签值为1的)的。
但针对混淆矩阵和这两个的含义不能死记硬背,不能硬生生的记左上角是TP,右下角是TN,y轴是实际情况,x轴是预测情况。如下:
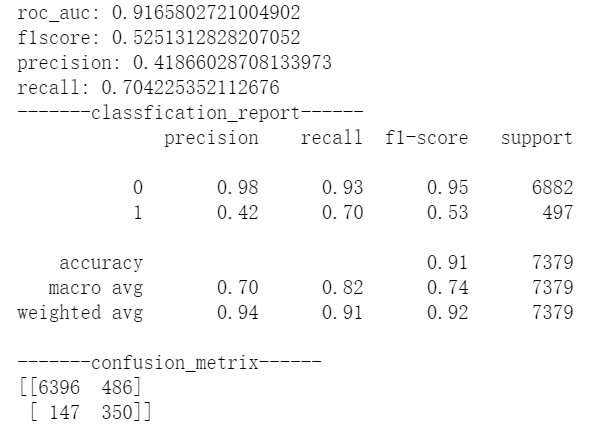
首先看classfication_report,可以看到Precision有两个值,分别对应0类和1类的Precision,而classfication_report上方输出的是这个模型通常看的四个指标也包含Precision,为了不混,叫做模型Precision吧。且1类的Precision=上方的模型Precision。
再往下看混淆矩阵,如果生搬硬套前文的混淆矩阵形式,我们很容易这样计算出模型的Precision=6396/(6396+147) 显然!= 0.48,而是=0.98=0类的Precision。这和我们说的模型Precision=1类的Precision不一致。
后来做了一些试验后发现,原来在sk中掉包出来的混淆矩阵,默许把类别多的放在左上角,因为我的数据中0类远远多于1类,所以在这个混淆矩阵中左上角代表的是TN,即把负类正确预测为负类的数量。所以还是得输出classfication_report看得更仔细一些。
❤什么时候看Precision,什么时候看recall?当然两个都高最好,在我的为数不多的经验来看,对于一些非常想揪出1类的项目来说,看recall,比如贷款逾期,非常想知道哪些人会逾期还款,这很重要,就看recall;但对于是猫或不是猫这种问题,看谁都无所谓。个人觉得,recall比较有实际意义,不太关心预测的方法好还是坏(会错杀多少我不关心),只想知道所有正类有没有被全部揪出来。
说到模型的判断指标,很容易想起
准确率accuracy=(TP+TN)/(TP+TN+FP+FN),这个比较好理解,就是分对的占所有样本的比重,也是最容易通俗的标准,看起来似乎很不错的样子。但是现在很多比赛都是样本极度不平衡的,比如0很多1很少,那么我只要把测试集中全部预测成0类,也可以达到很高的TN,导致准确率很高,但这种模型没有意义,不能衡量模型的好坏。所以对于样本不平衡的数据,通常看recall比较好。Precision和recall就是在这种时候衍生出来的(真是天才)
前面说到Precision又叫查准率,recall又叫查全率,再复习一次Precision是针对预测结果的;而recall是针对实际情况的。查准率和查全率这个名字其实更能够体现其本身的含义:我预测的准不准;我查的全不全。
| Precision | 精确率 | 查准率 | TP/(TP+FP) | 分母是预测全为正的样本 | 针对预测情况 |
| recall | 召回率 | 查全率 | TP/(TP+FN) | 分母是实际全为正的样本 | 针对实际情况 |
图2
对于查准率和查全率有一个曲线为P-R曲线,其实就是Precision-recall曲线,接下来解读一下这个曲线:
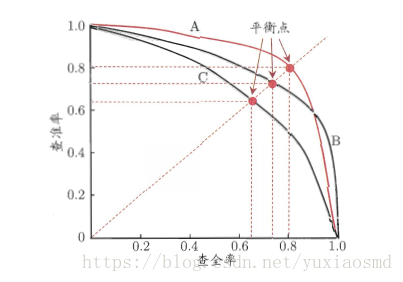
图3
开始看到这个曲线很迷惑,在我之前的认知里:一个模型,有几类就有几对Precision-recall,其中拿一类比较重要的当模型指标而已。但是在上图中Precision-recall怎么会组成连续的曲线?像二分类至多有两组Precision-recall这要怎么办?
原来不能按照以前学数学的时候xy轴来看这个图。上图里的每个点代表每一组Precision-recall,每一组Precision-recall都是在某个阈值下计算出来的。通常分类模型的输出是一组0-1之间的概率,概率越大越接近正类,越小越接近负类,而不是直接输出0类和1类的结果,比如对于一条数据,通过分类模型中得到的概率是0.49,此时我们不能说它是负类,因为你没法解释为什么0.49是负类,你需要给个事前说明:低于0.5(阈值)的属于负类;但是更改这个阈值设定的话,老师告诉你,低于0.3(阈值)的才可以认定为负类,那么这条数据就变成了正类。这条数据是正类还是负类会影响Precision-recall。
接下来就可以遍历0-1之间的所有阈值,得到多组的Precision-recall组成了P-R曲线,那么阈值究竟定多少为好,前面有说,通常情况下我们希望Precision-recall两者都高,不要有一方高一方不高的情况,那么就让两个一致就好了,于是画了一条Y=x的直线,相交处的阈值是最佳的,因为此时Precision-recall相等。
但通常,如果想要找到二者之间的一个平衡点,我们就需要一个新的指标:F1分数。F1分数同时考虑了查准率和查全率,让二者同时达到最高,取一个平衡。F1分数的公式为 = 2*查准率*查全率 / (查准率 + 查全率)。我们在图中看到的平衡点就是F1分数得来的结果。精确度和召回率都高时, F1 F1值也会高. F1 F1值在1时达到最佳值(完美的精确度和召回率),最差为0.在二元分类中, F1 F1值是测试准确度的量度。
三、roc/auc曲线
灵敏度(Sensitivity) = TP/(TP+FN)=召回率
特异度(Specificity) = TN/(FP+TN)
真正率(TPR) = 灵敏度 = TP/(TP+FN)
假正率(FPR) = 1- 特异度 = FP/(FP+TN) #特异度其实用到的比较少,因为通常比较关心正样本
可以看到TPR FPR都是针对实际情况而言的,因为分母出现了四个不同字母(再次复习!)对于实际情况,真正率和假正率在名字上就告诉了我们分子是谁,而分母都包含其分子。所以只要先根据名字写出分子,继而写出分母就好。
根据前文,我们依然固执的认为一个模型里就一组真正和假正,毕竟其算式里的每个数都是固定的;其实不然,只要像PR曲线里的思想一样,取多个阈值,依然可以得到一组TPR-FPR曲线(roc曲线)。
ROC曲线的绘制步骤如下:
- 假设已经得出一系列样本被划分为正类的概率Score值,按照大小排序。
- 从高到低,依次将“Score”值作为阈值threshold,当测试样本属于正样本的概率大于或等于这个threshold时,我们认为它为正样本,否则为负样本。举例来说,对于某个样本,其“Score”值为0.6,那么“Score”值大于等于0.6的样本都被认为是正样本,而其他样本则都认为是负样本。
- 每次选取一个不同的threshold,得到一组FPR和TPR,以FPR值为横坐标和TPR值为纵坐标,即ROC曲线上的一点。
- 根据3中的每个坐标点,画图。
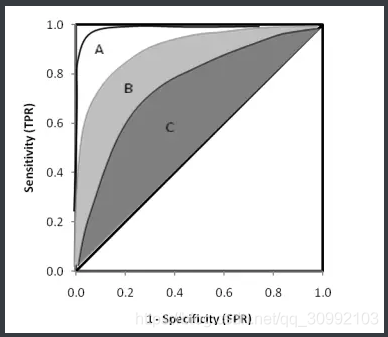
图4
roc上的每一点,都表示一个阈值下的一组TPR FPR,思想不多赘述。
那么怎么样通过这个曲线看模型好不好呢,可以很自然的知道,TPR越高越好,FPR越低越好,最好的点就是左上角(0,1),最差的点就是右下角(1,0),所以可以采用auc(曲线下的面积)大小来衡量模型的好坏,auc越大,代表曲线越靠上,模型越好。
连接对角线,它的面积正好是0.5。对角线的实际含义是:随机判断响应与不响应,正负样本覆盖率应该都是50%,表示随机效果。ROC曲线越陡越好,所以理想值就是1,一个正方形,而最差的随机判断都有0.5,所以一般AUC的值是介于0.5到1之间的。
❤auc的物理意义:
曲线下面积对所有可能的分类阈值的效果进行综合衡量。曲线下面积的一种解读方式是看作模型将某个随机正类别样本排列在某个随机负类别样本之上的概率。以下面的样本为例,逻辑回归预测从左到右以升序排列:
参考:






