【论文笔记】Truth and Cognitive Division of Labour First Steps towards a Computer Aided Social Epistemology
Truth and Cognitive Division of Labour First Steps towards a Computer Aided Social Epistemology
摘要
本文分析了在认知分工(cognitive division of labour)与社会交换过程(social exchange process)相结合的条件下,真理被发现并被广泛接受的机会。认知分工意味着,只有一些人是积极的真理寻求者,可能具有不同的能力。社会交换过程包括所有个人之间的意见交换,无论是否寻求真理。我们建立了一个模型,通过数学工具和计算机模拟进行了研究。作为一个分析结果,漏斗定理指出,在相当弱的社会过程条件下,如果所有人都有一个任意小的求真倾向,那么真理就会达成共识。领导包定理指出,在某些条件下,即使是一个真理寻求者,也可能会带领所有人找到真理。系统模拟分析群体接近真相的程度和速度,这取决于真相寻求者的频率、他们作为真相寻求者的能力、真相的位置(更极端或更集中在意见空间的中心)以及在交流和更新时考虑他人意见的意愿意见。一部棘手的电影将模拟结果可视化,得到了更高维度的参数空间
1.介绍
2.case1:真相寻求者的意见动态变化
这节主要是通过几个仿真图模拟了一下在有界信任条件下,观点在不同情况下收敛到正确时的情况,先是展示了有界性任下没有真理追求者($\alpha _{i}=0$,也就是不考虑观点的正确与否时)的观点收敛情况,发现小社团会各自形成小观点,整体看来,不能达到收敛到一致,但是可以保持平稳不变(Figure 1),其中虚线部分表示真理值,相邻两个个体的观点之间的灰色区域表示它们的观点之差不大于$\varepsilon $,,根据有界信任模型的规则,也就是说两个个体之间可以交流:

这个图遵循的是以下公式:
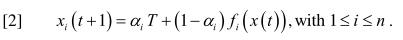
其中T代表真理,也就是我们的正确观点,前面的系数$\alpha _{i}$代表着对T的一个吸引力,而$f_{i}(x(t))$代表着社会因素,也就是网络中其他人的观点的影响,可以是一个加权求和的值,这里的社会因素是基于有界信任模型的,也就是说两个个体的观点,只有差值小于阈值才可以进行交流。
先定义两个词,叫做$\varepsilon -profile$以及$\varepsilon -split$,前者是说在某个时间节点上二者的观点相近,可以交流;后者是说在某个时间节点上二者的观点相去甚远不再交流。在1-14图中,甚至有的图的观点最开始都没有$\varepsilon -profile$。分离的子剖面(sub-profile)属于不同的“观点世界”,它们在下一时刻不再交流。一个子剖面上的观点若收到了片面的影响朝着sub-profile的中心移动,结果就是sub-profile的范围越来越小,在极短情况下,意见是浓缩(condense)的。如果是观点较为密集的部分的意见可能会在子剖面的下一时刻继续分裂。最后这个社会过程就是这样的:在 split sub-profile中,每个人的观点都是在他人的观点阈值内,所有意见在下一时刻都会融合成一个意见。此时开始,所有的观点就稳定了。在图一中,稳定性意味着永恒的多种不变的观点。
在Figure2中,与1的区别在于,我们增加了一点点对真理的关注度$\alpha _{i}$,现在所有的个体都是真理追求者(truth seeker)了。所以可以比较我们提出的【2】这个公式和单纯的有界置信模型(BC)之间的差别了。在图1中,真理T的存在完全没有影响观点动力,而在图2中,很明显整个社会都是由T来驱动的。时间治愈了$\varepsilon -split$,这些观点在有限的时间内融合在一起。我们可以看到,大家的观点在朝着真理T的位置发展。观察结果如下:

就是说在某些条件下,追求真理的个体会达成很接近真理的共识。
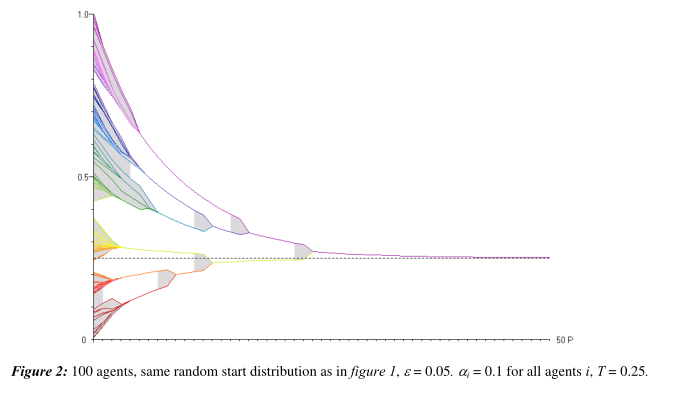
然后我们就会想,要达成真理,一定要每个个体都都是真理追求者吗?出于这种想法,就模拟了以下的图3和图4(注意原文图4和5反了,所以图片中的图4在本篇博客中实际上是图5)
在图三中,只有一半的个体是真理追求者。
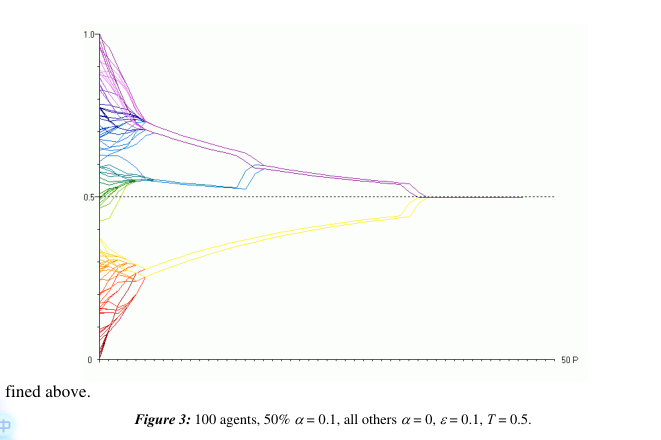
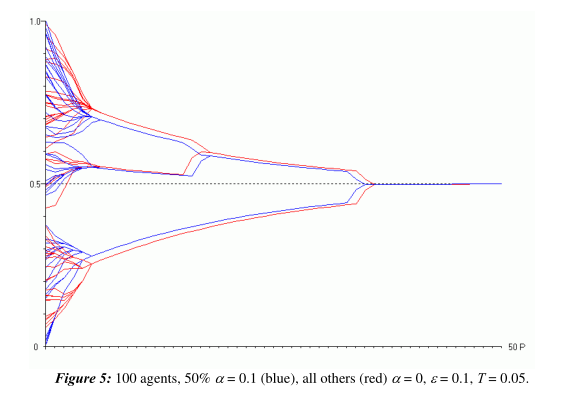
在上述图4中,红色代表真理追求者,我们可以很清楚看到它们的演变过程。
然后根据图3和4我们得出的观察结果如下:
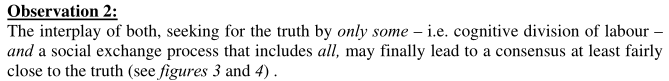
也就是说,如果只有一部分人去追求真相(认知分工),然后其他人就在做普通的BC模型中的观点社会交换,那么还是有可能达成共识的。
接下来我们看图5,图5的其他设置都一样,只是改变了真理,在前面的图中,T=0.5,真理是一个比较中立的观点,而现在我们更改观点为T=0.05,是一个比较极端的观点。
我们就发现,大部分的人还是有可能收敛到正确观点的,但是有一些离观点太远的另一个极端的观点,就会被落下了。

这个观察结果是说,对于2的结论,如果真理比较极端的话,共识也有可能不达成。
接下来继续思考,这个对于真理的追求速度是否也有影响,如果有些人追求真理的速度更快一点,能不能更快达成共识?
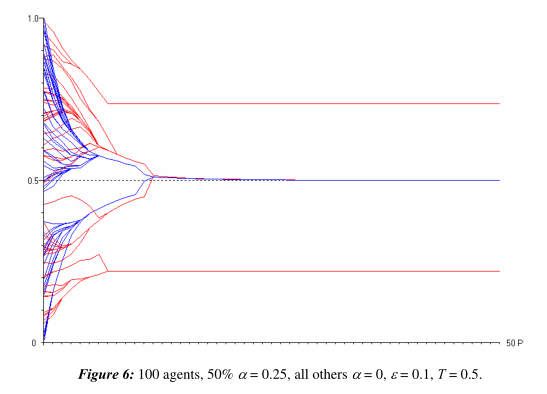
结果就是,虽然一部分人也能融合观点,但是一些初始观点较为极端的个体还是被扔下了。

所以又对观察2进行了补充说明,表示追求真理的速度也很重要。
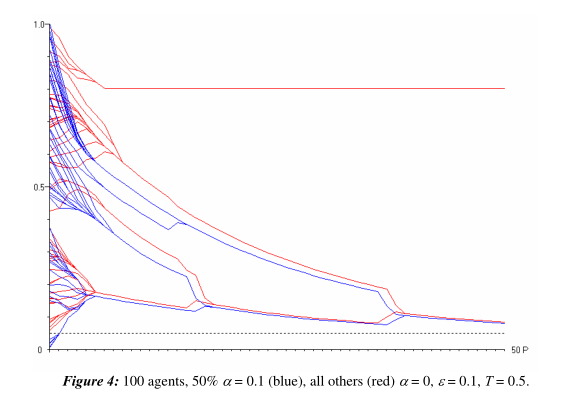
接下来考虑置信水平,可想而知,如果置信水平很高,大家容易信任对方,那么达成一致的可能性和速度可能更高,图7除了置信水平外都和图6的设置相同:
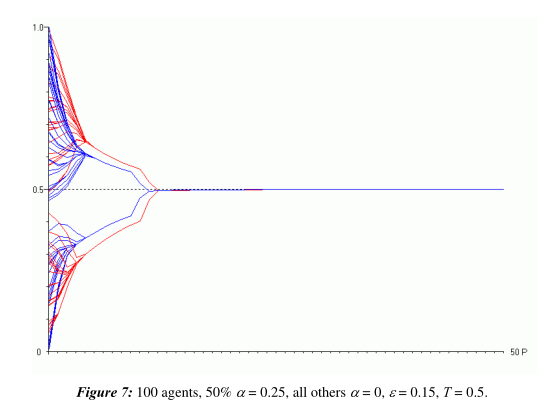

所以我们可以说,如果对真理的追求速度过快,导致有的个体跟不上的话,那么我们可以考虑增大置信水平,也可以促使一致。
但是如果没有足够的真理追求者呢?如图8所示:
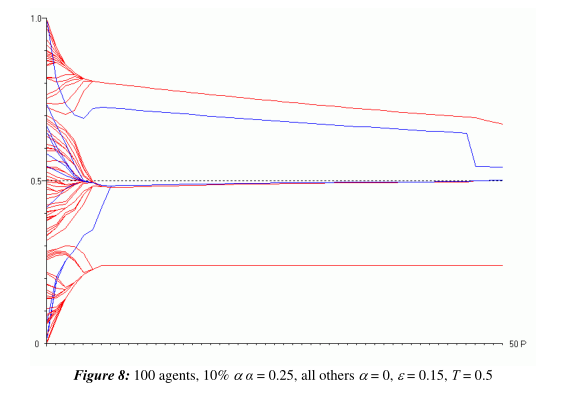

所以说,基于一定百分比的真理追求速度达成的观点一致,若百分比改变,观点也有可能不一致。所以百分比很重要
我们的单次模拟似乎表明了两个普遍的观点:首先,如果BC-模型管理的社会交换过程中的所有代理都是真相寻求者,那么他们最终会对真相达成共识。第二,在认知分工下,即并非所有人都是α-阳性,最终能否就真理达成共识,关键取决于α-阳性的频率、真理的位置、置信水平ε和α的值,即真理吸引力的强度。在下文中,对这两种观点进行了详细分析。
3.保持距离的真相追求过程:漏斗定理
这段主要是限制了观点的极大值和极小值,在这个背景的前提下进行研究。如公式【3】所示:
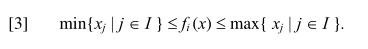
这个假设想告诉我们的是,所有人,在执行社会交流过程中,所得到的新的观点值,都会在上一时刻的观点范围内变动,不会超过这个范围,这个也叫做range preserving social process保留的社会过程。然后还有一种是LW和BC模型都遵守的社会过程如下:
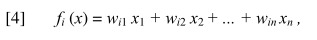
这个fi,可以理解成节点i在下一时刻的一个社会交流过程,如【4】所表达的,节点i它受到的社会影响,就是网络中其他节点的观点的影响,这里不用xi来表示观点主要是为了区分上一时刻和下一时刻。xi可以理解成当前的观点,而fix就是下一时刻节点i受到了其他人的社会影响而产生的观点。然后这里的权重wij是在0-1之间的。
如果是在BC模型中,它的这个权重根据规则来制定:
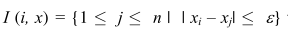
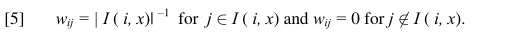
这个规则告诉我们,我们只要去看观点值和节点i相近的节点即可为观点值分配权重,比如节点i有6个节点的观点和它相近,那么就分配1/6给它们,这里是均分,然后其他节点就没有份。
因为【4】中权重之和为1,所以它是符合我们【3】中的要求的;如果我们不适用【4】中的加权平均,换成其他平均只要能满足【3】的要求,就可以。满足【3】的权重我们叫抽象平均值abstract mean。
加上前面的公式【2】,我们可以得到:
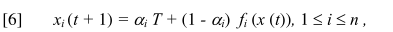
注意f还是一个保留范围的社会过程,要符合我们第三节的大前提。
现在我们的问题是:个体i的观点是否接近我们的真理T,很显然这肯定和$\alpha _{i}$有关,如果$\alpha _{i}=1$,那么个体不用和别人交流,下一时刻它就可以找到T;如果$\alpha _{i}=0$,那么它的意见就完全取决于社会过程。所以我们考虑$0<\alpha _{i}<1$这种情况,个体i的意见与真理T有关,也与其他人的观点有关。严格的说,最后接近真相也取决于大家最初的观点值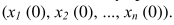 。因为如果最初大家的观点都是T,那么就没有什么假设的必要了。在下文的描述中,“接近真相”是对每个个体原始观点的描述;然后现在介绍一个“漏斗定理”,用来描述观点是怎么样逐渐合成并且在确定的“漏斗”中最终趋于真理T的。
。因为如果最初大家的观点都是T,那么就没有什么假设的必要了。在下文的描述中,“接近真相”是对每个个体原始观点的描述;然后现在介绍一个“漏斗定理”,用来描述观点是怎么样逐渐合成并且在确定的“漏斗”中最终趋于真理T的。
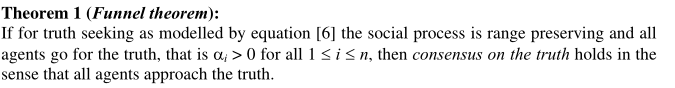
这个定理就是基于公式【6】所描述的过程,如果社会过程是保持范围的,也就是说当前社会影响下的观点不超过上一时刻的观点范围(就像一个漏斗一样),并且所有的个体都追求观点,那么对真理的共识就认为所有个体都会接近真理。证明如下:


这个证明算是简单的,用到了数学归纳法。u和v不是具体的某个个体,而是当前时刻的最小观点和最大观点值。上述证明了,接下来个体i在任何时候的观点都不会超出历史上出现的的最大上界和最小下界的观点值。这就把观点限制住在一个范围里了。
下面讨论T和初始观点值的位置对收敛到真实值的影响,因为上一节说了T的位置有可能影响收敛,现在引入了漏斗的upper和lower,重新再来审视一遍:
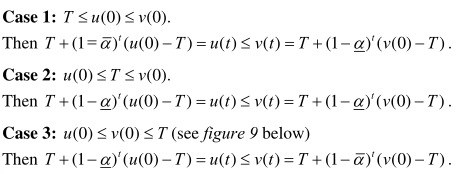
因为不等式左右两边都收敛于T,所以很简单漏斗的下壁和上壁在所有三种情况下都收敛到真值T。更确切地说,在漏斗中捕获的个体的意见都必须收敛到T。
这里为什么有个$ \bar{\alpha}$和$\alpha$呢?前者表示$\alpha$中最大的那个,后者表示最小的$\alpha$。要理解这个就得时刻告诉自己u是最小的,v是最大的。既然如此就好理解我们的公式了,比如case1中的Then部分,左边计算u时,是用的$(1- \bar{\alpha})$,实质上这个公式可以推出来,多写两三步套用一下即可,关键就是为什么这里$\alpha$换成了$ \bar{\alpha}$,主要原因是,T<u(0),则u(t)是下界,也需要靠近T,但是呢,因为它是最小的弟弟,其他人都得比它大才可,于是乎,它就只能分到了一个最小的权重,也就是$(1- \bar{\alpha})$,case23中的Then同理,只是要注意这里T>u(0)了。故这三个假设没毛病,现在要讨论这三个假设。
下面通过模拟说明上述三种可能性中的情况3。虚线描绘了T的值,黑色的是漏斗的上下壁。漏斗内的彩色曲线显示个体们的意见趋于一致,接近T:

从漏斗定理可以得到一个推论,有关最大距离和时间的关系:

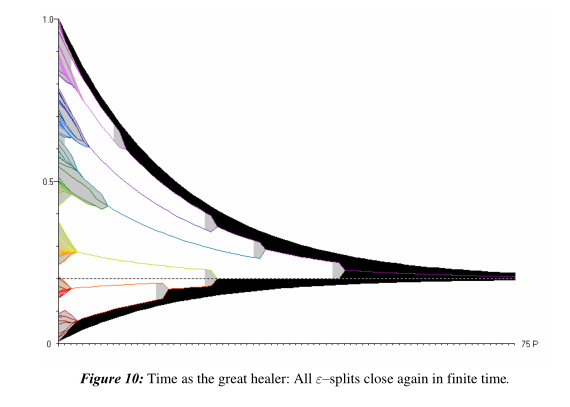
从上图看出,原本已经分离的观点在有限的时间里又融合了。
漏斗定理的一个显著特点是,特别是上述推论,如果只有社会过程动力学,其观点将永远分离的主体,如果是α-正的,即如果他们追求真理,就会任意地靠近在一起。
4 时变过程的真理追求:包的领导定理
漏斗定理是认为所有个体都追求真理的情况下做出来的结论,在图3,4,7中,已经假设过只有一半的个体追求真理的情况了,可以发现他们能够带领所有人达成正确观点。在这一节中将分析得出即使只有一个个体追求真理也能得出正确观点一致的情况,只要他拥有足够的信心。这个结果不适用于一般的社会保留过程(像3的假设),适用于某些时变的社会过程,仍然包括有LW和BC模式。依旧用公式【6】,社会影响改变了:
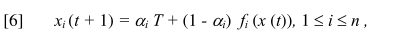
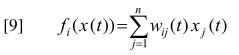
【9】这个公式和前面的【4】的区别就在于权重可以随时间变化。
定义一个“从个体i到个体j的在(s,t)时间间隔内的置信链confidence chain from agent i to agent j for the time interval (s, t) ”:“存在一组个体链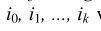 ,其中i0=j,ik=j”,且有权重
,其中i0=j,ik=j”,且有权重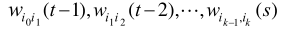 严格为正。这个想说明的是:如果个体j在s时刻能够影响$i_{k-1}$,然后在s-1时刻,$i_{k-1}$又可以影响$i_{k-2}$,在下一个时刻s-2$i_{k-2}$又可以影响$i_{k-3}$,以此类推,直到最长时间间隔s-t时,即t-1时刻,$i_{1}$可以影响$i_{0}$,也就是节点j经过了漫长的时间终于影响了节点i。这是考虑了时间的因素,所以它是在时间间隔内的一个置信链。
严格为正。这个想说明的是:如果个体j在s时刻能够影响$i_{k-1}$,然后在s-1时刻,$i_{k-1}$又可以影响$i_{k-2}$,在下一个时刻s-2$i_{k-2}$又可以影响$i_{k-3}$,以此类推,直到最长时间间隔s-t时,即t-1时刻,$i_{1}$可以影响$i_{0}$,也就是节点j经过了漫长的时间终于影响了节点i。这是考虑了时间的因素,所以它是在时间间隔内的一个置信链。

假设存在一些时间间隔$t_{m}$,时间间隔之间的差值也就是它们的长度的差值在2-r之间,对于每一个不追求真理的个体,如果它在某个时间间隔内,能够有一条通向真理追求者的置信链,那么就能够实现真理共识。就像是,一个差生,如果他所在的朋友圈里有一个优等生,那么他也会多多少少被感染一些。

不可约矩阵的定义如下,意思就是非负矩阵对应的有向图是强连通的:
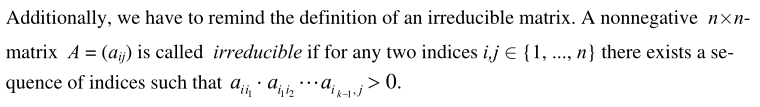
对于BC模型,还需要满足有界性:
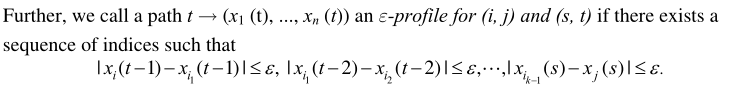
对于上面这个结果是建立在至少有一个个体是寻求真相的,不然就变成了普通的观点动力学。所以仅仅不可约是不足以达成真理共识的。但是对于上面定理2的(a)部分,减弱形式的不可约矩阵就够了。
接下来一个例子说明,对于可约矩阵,(a)的说法可能失败,也就是说不存在那样一条置信链的时候:

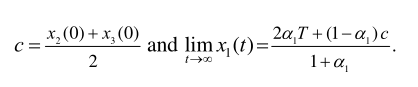
所以,2和3达成了共识但是却不确定是不是T,除非c=T。
现在更改一下条件,上面这个条件是$0< \alpha _{1}< 1$和$\alpha _{2}=\alpha _{3}=0$,现在我们让$0< \alpha _{2}< 1$,其余条件不变,则现在只有3是不追求真相的人,2有一条追求真相链,因此根据定理2肯定能达成真理共识,也就是说只要$\alpha _{2}$和$\alpha _{2}$为正,不需要它们具体是什么数值。这个结果不是由定理1也不是定理2得出来的
接下来说明定理2的(b)部分,
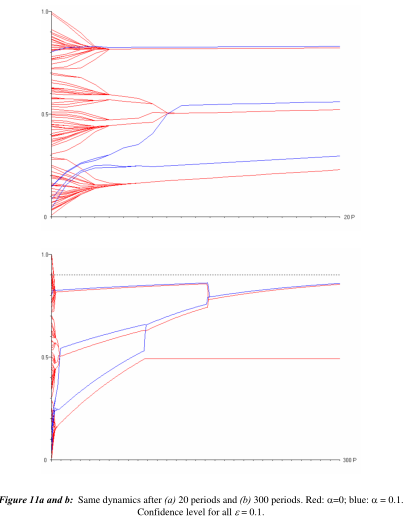
蓝色代表追求真理,红色代表不追求真理。根据领先的包定理,关于真相的一致性问题(对于所有个体)只取决于最终红色是否与蓝色相连。在图11b中,最低的红色组永远不会与蓝色连接。因此,对于包括所有人在内的真相,不会有任何共识。
5 case2:参数空间的真理偏差
领先的包定理暗示了BC-模型在某些条件下,很少甚至只有一个真理探索者可以带领包找到真理。但我们什么时候才能期望这些条件得到满足呢?如果这些条件得不到满足,动力倾向于在哪里结束?通过第二章中的案例研究,我们已经知道,对真理达成最终共识的机会,在很大程度上取决于α-阳性的频率、真理的位置、置信水平ε和真理吸引的强度α。因此,我们面对的是一个四维参数空间。在本章中,我们将通过系统仿真来分析该参数空间。指导性的研究问题是:在动力学稳定后,我们在参数空间中期望的平均真值偏差是多少?真理偏差可以用不同的方法来衡量。这里采用标准差,定义如下:
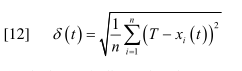
分析四维参数空间是一项非常困难的任务。因此,所有其他的事情都尽可能简单:我们假设,第一,齐次的,对称的,恒定的置信水平ε对于所有个体,第二,齐次的,恒定的α对于所有α-阳性个体,第三,固定数量的100个个体,第四,均匀的开始分布,最后,同步更新。
在四维参数空间中的平均真值偏差的模拟结果将被可视化,以便快速和容易地理解我们的案例研究。更详细地说,我们将按如下方式改变参数:
- 真理的值T:
![]()
- 不追求真理者的频率F:
![]()
- 置信水平ε:
![]()
- 真理吸引强度α:
![]()
对于T和F,仿真策略是一种情景方法。真理可能在意见空间的中心,真理可能是一个极端或介于两者之间。几乎所有、一半或只有部分特工可能是非真相探索者。总共是3×3个场景。对于ε和α,我们采用40×100点的网格方法。图12解释了组合场景和网格方法。
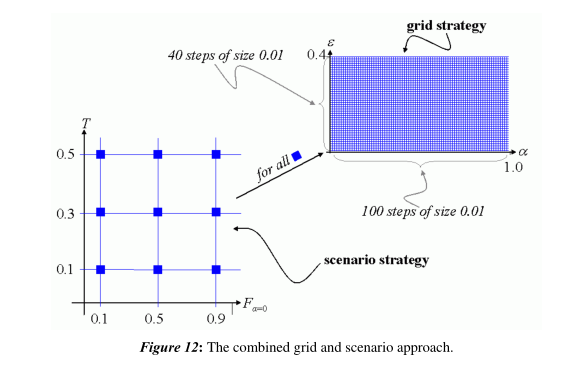
对于3×3场景中的每个40×100网格点,我们运行50个模拟,直到动力学稳定。然后计算平均真值偏差,并用颜色对数值进行编码。因此,所有的模拟结果都可以用图13给出的一个巨大的图形来表示。
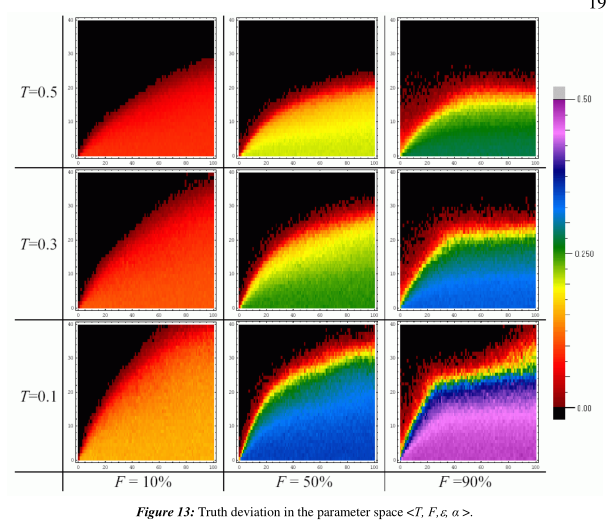
图13中最引人注目的是所有场景中的巨大黑色区域。在参数空间的这些区域中,平均真值偏差为0。因此个体们最终就真相达成了共识。

无论真理在哪里,无论是极少数人,甚至是绝大多数的真理寻求者,在对真理的信心水平和吸引力的适当价值观下,整个社会最终都会对真理达成共识。对于这种关于真理的共识,必须在ε和α之间有正确的比例。

对于几乎所有的T、F和α,置信水平似乎都有一个临界值ε*,因此只有当ε>ε*,才有可能就真理达成共识。必须超过的临界置信水平随着真理吸引强度α的增加而增加。如果真理在意见空间的中心,那么临界置信水平低于更极端的真理。除了情况之外,对于给定的真值位置,如果F增加,临界值ε*似乎略有降低。

对于几乎所有的T,F和ε,真理吸引力的强度似乎都有一个临界值α*,因此对于真理的共识,α<α*是必要的。如果真相在中心,并且置信水平足够高,那么任何α都将达成共识。在大多数情况下,不能超过的临界值α*随着置信水平ε的降低而减小。可能是,对于F=90%和低置信水平,只有当α值远小于我们在模拟中使用的值时,才有可能对真相达成共识。
并不是所有的参数最组终都会在真相上达成共识。似乎有些情况下,至少要接近真相是比较困难的:

如果对于某个参数组,在所有情况下都存在正的真值偏差,那么对于更高的频率F和更极端的真值T,这些真值偏差往往更高。
对于大多数观察结果的解释,有必要理解两种影响:第一种可能被称为“附带效应”take–along–effect:即使是一个真理探索者,也可以通过与其他人一起,将整个社会推向真理。这种效应也适用于α-阳性的少数人。更普遍的是:通过社会交换过程,真相寻求者可以带着那些不追求真相或不成功的人一起去寻找真相。但在这种情况下,α和ε的值必须具有正确的比例:给定一个置信水平,真理的吸引力不能太强;给定真理的吸引力,置信水平必须足够高。图14a(上图)给出了一个例子。在这里,一个孤独的真相寻求者沿着所有其他人的方向T。第二个效应的作用方向相反:真相寻求者可能“太好”了,不能和其他人一起。图14b(底部)给出了一个例子。在这里,一小群非常优秀的真理寻求者很快地穿越了整个意见空间,朝着一个极端真理的方向前进。虽然一开始分散在整个舆论空间,但他们留下了一个两极分化的社会,他们的意见并没有产生重大影响。这种效应可以称为留守效应leaving–behind–effect。

图13显示了动力学稳定后的真值偏差。但真相偏差是如何随着时间的推移而发展的呢。下面的电影给出了一个基于模拟的答案。它的51张图片中的每一张都有图13所示的结构,并显示了直到第50个周期的真理偏差。与图13不同的是,在电影中,置信度按50步进行分析,直至ε=0.5。
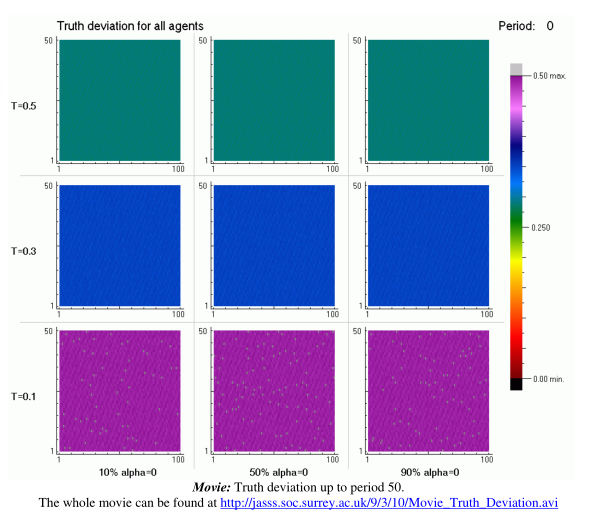

观察11:在所有情况下,它都在右上角,即高置信水平与强真理吸引相结合的区域,在该区域,真理偏离开始显著减少。这种下降向左侧扩散,即向不太强的真理吸引方向扩散,向底部扩散,即向较低的信心水平方向扩散。
观察12:如果真相在中心T=0.5和/或对真相不感兴趣的个体的频率很小(F=10%),那么真相偏差下降得特别快。
观察13:稳定后的最终结构,如图13所示,出现得很早。对于较小的α值,可以发现与最终结构最显著的差异。如果真相更极端和/或追求真相的代理人的频率很小,则差异就更严重
6 展望
- 人们可以把注意力集中在传播真相的困难情况上,例如立场远离真相、对真相不感兴趣的意见领袖,对真相有偏见的置信区间,或者在开始分布中出现远离真相的峰值。
- 可以放弃对T的相当乐观的理想化假设。例如,新的证据可能指向两个或多个不同的方向。
- 我们把真理的吸引力视为既定的力量。另一种观点可能是将α视为一个受干预影响的参数。在这样一种观点下,人们可能会开始思考有效的真相扩散政策:在意见范围内,人们应该向真相寻求者提供多少代理人,以便使社会的所有人或至少相当一部分人相信真相?如果有时间压力呢?如果社会交换过程具有以本地交互为主的网络结构,该怎么办?
- 在本文中,有界置信模型发挥了重要作用。但总体框架并不一定与BC-社会过程模型相关联。也有其他机制,例如不保留范围的机制



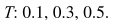
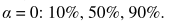
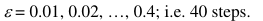
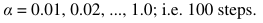

 浙公网安备 33010602011771号
浙公网安备 33010602011771号