深度学习(二):图模型的学习
一、前言
图模型的学习主要是学习网络结构,即寻找最优的网络结构;以及网络参数估计,即已知网络结构,估计每个条件概率分布的参数。这里主要讲网络参数的估计。然后又可以分为不含隐变量的参数估计,和含隐变量的参数估计。隐变量相对于可观测变量而言,就是我们无法直接观测到的变量;在特征空间里可以理解为不能被人直接看到的、更高级的需要进行推理才能知道的特征。
二、不含隐变量的参数估计
在有向图模型中,如果所有的变量都是可观测的,而且还知道谁是谁的条件(父节点),那么估计网络参数只要通过最大似然来估计就可以了:
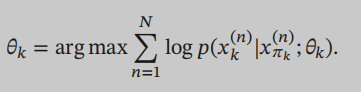
为了减少参数量,可以用参数化模型,如果是离散的可以用sigmoid信念网络,如果连续的,可以用高斯信念网络(解答了上一个博文的疑惑,原来高斯概率分布也是可以用的,主要取决于变量x是离散还是连续的)
在有向图中,x的联合概率分布就要拆解成最大团上势能函数的连乘形式了:
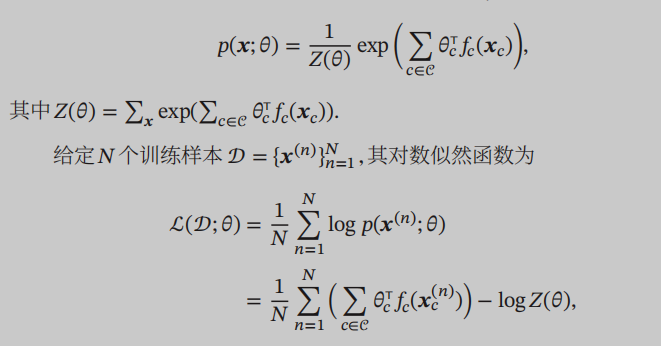
对这个对数似然函数的参数theta进行求导,可以发现对配分函数Z求导时,得到的结果是在模型分布下的期望:
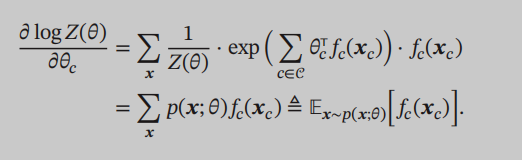
这里的模型分布指的就是最开始我们定义的P(x),是这些样本所服从的概率分布,而我们的目标就是求得这个未知模型的参数。
然后我们会发现:

第一项不免会让人想起刚刚学不定积分的时候,积分最开始是用长方形的面积来进行引入的。第一项其实可以称为经验分布,也可以写成期望的形式:
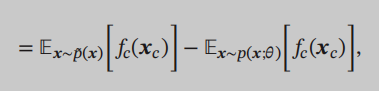
前者是经验分布,是我们通过实际的样本得到的,后者是模型分布,是我们需要求的。我们最开始求导是为了令导数等于0,求出参数,所以无向图模型中,求导这个过程就等价于我们在通过样本来拟合真实分布。
三、含隐变量的参数估计
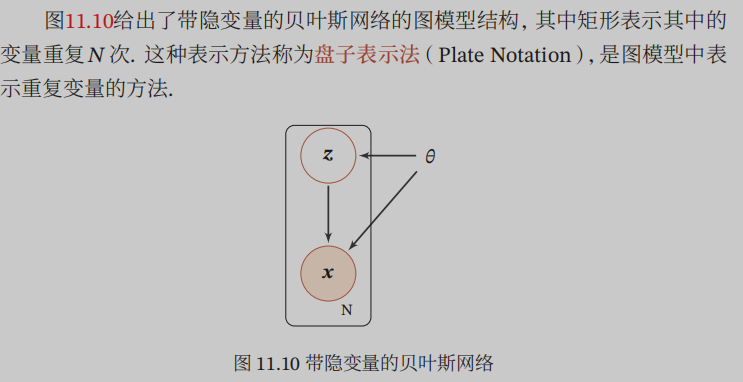
这样的模型中即含有隐变量也含有可观测变量,但要永远记住隐变量是我们看不到的变量!那我们能用的数据样本只有可观测变量!没有隐变量!因为隐变量看不见!知道了这一点就很好理解接下来的工作了!
其实我们要求的最终目的只有p(x),x指的是可观测变量,隐变量用z来表示,首先我们没法求p(z),其次求了p(z)也没有什么现实意义,好比我们正常人吃饭的终极目的是为了活下去,而不是为了观察饭是怎么样在肚子里消化的,虽然有研究者研究这些才丰富了我们的医学宝库,但是研究者他们研究这个的终极目的是科研,人家吃饭也是为了活着!
那怎么求p(x)呢,我们现在知道模型里有两种随机变量,可观测和隐,然后他们之间会有相互关联,但我们只能看见可观测的随机变量,看不见隐,但是隐变量也是随机变量,它们也会影响我们的可观测变量的概率,虽然我们没必要去弄清楚隐变量具体是怎么分布的,但是我们在考虑可观测变量的概率分布时不得不考虑到隐变量对其的影响。
定义样本x的边际似然函数为:$p(x;\theta )=\sum_{z}^{ }p(x,z;\theta )$
这个公式告诉我们,如果想要知道可观测变量x的概率分布,只要对可观测变量x和隐变量z的联合概率再对z求和就好了,其实就是求x的边际概率,因为这里随机变量非x即z,x的边际概率就是联合概率对z求和。之前看到这里的时候觉得好废话啊,我要是能知道联合概率分布,那肯定就能求出来了嘛,但是关键是看不见隐变量,没法先求联合概率分布再求和嘛,按照这个思路,如果依然用前面不含隐变量的图模型中提到的似然法的话,要最大化似然估计:
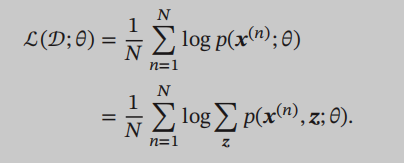
即便是对这个似然函数直接求导,我们也发现,log求导后,联合概率分布会跑到分母处,我们没办法消掉这个我们计算不出来的联合概率分布。这个求和没办法直接计算,就会引出一个问题叫做推断问题,其实推断问题主要就是计算条件概率分布$p(z\mid x;\theta )$,为什么要计算这个呢,因为联合概率分布$p(z,x;\theta )=p(z\mid x;\theta )p( x;\theta )$,为什么联合概率分布没法算主要是涉及对z求和,我们把联合概率分布按照条件概率公式分解后,其中含z的项就是条件概率分布$p(z\mid x;\theta )$,如果我们计算出了这个值,似然函数也没问题了。推断有精确推断和近似推断,然后还有很多引申出来的知识,放在其他博文写。
现在似然函数退一步,不到对Z求和的那一步,似然函数主要是要计算$log p(x;\theta )$,先引入ELBO证据下界的定义:

这里不等号成立主要是因为:对于像log这种上凸的函数(国际上叫凹函数,跟我国高中课本理解相反),函数的期望小于期望的函数,这个学过经济学应该会好理解一点。看上面不等式小的一方,它变小了主要是因为原来在log里面作为自变量之一的概率q离家出走了,变成了函数的期望,函数的期望是个期望,它不在函数线上,而期望的函数好歹还是函数,在log曲线上,画图说明如下,这里之所以取的是a+b/2,主要是为了好画图,默认这里服从的分布是均匀分布,也就是默认上式中的概率分布q是均匀分布:

不过书上提到一个jensen不等式来解释这个不等式,但是能理解就行,真是还好学过经济学。。
回到ELBO证据下界,考虑证据下界何时最大,只要这个变分函数满足$q(z)=p(z\mid x;\theta )$就可以了,具体证明可以自己推一下,只用到条件概率公式。
所以最大化$log p(x;\theta )$可以转换为两步走:1.找一个近似分布满足$q(z)=p(z\mid x;\theta )$,此时证据下界最大;2.想办法找到参数theta,使得证据下界最大。
1.决定了证据下界等于$log p(x;\theta )$,最大化证据下界就等价于最大化$log p(x;\theta )$;2.决定了证据下界取最大值。
可以用EM算法来做这两件事情,EM算法会再另开机器学习的文章说明,EM算法是含隐变量图模型的常用估计方法。EM算法在这里就是:
(1)E步:先固定参数theta,找到一个分部$q(z)$,使得证据下界等于$log p(x;\theta )$;我们已经说明最好的$q(z)$是后验分部$q(z\mid x;\theta )$,but计算这个后验分布是一个推断问题,在复杂情况下需要用近似推断的方法来估计。
(2)M步:然后固定我们找到的分布$q(z)$,开始找到一组参数使得证据下界ELBO最大,即优化:

然而,最大化证据下界可以等价于最小化KL散度,这个也更好的说明了为什么$q(z)=p(z\mid x;\theta )$时证据下界最大:

以下是迭代时各个值的过程:

四、高斯混合模型
高斯混合模型(GMM)是由多个高斯分布组成的模型,其总体密度函数为多个高斯密度函数的加权组合,如果一个连续随机变量或连续随机向量的分布比较复杂,我们可以用高斯混合模型来估计其分布情况,因为高斯分布从前人的经验来看是可以很好的估计出很多概率分布。哎之前就一直不知道为啥就可以用高斯分布去估计别的分布。
混合高斯模型的概率密度函数:

高斯混合模型表示成无向图,其中的隐变量就是样本x主要从哪个高斯分布里取值,因为高斯混合模型其总体密度函数为多个高斯密度函数的加权组合,我们把计算样本x的概率分两步走,第一步找具体哪个分布,第二步才是套用公式:

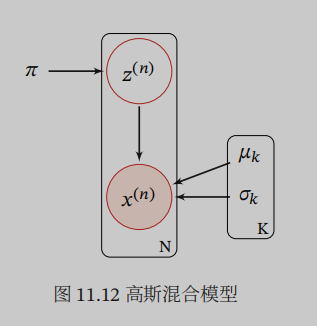
因为存在隐变量所以没法直接最大似然估计:


然后日常求导等于0就可以计算出来三个参数了



