拟牛顿法 分析与推导
针对牛顿法中海塞矩阵的计算问题,拟牛顿法主要是使用一个海塞矩阵的近似矩阵来代替原来的还塞矩阵,通过这种方式来减少运算的复杂度。其主要过程是先推导出海塞矩阵需要满足的条件,即拟牛顿条件(也可以称为拟牛顿方程)。然后我们构造一个满足拟牛顿条件的近似矩阵来代替原来的海塞矩阵。
另外,在满足拟牛顿条件的基础上如何构造近似的海塞矩阵,这有很多种方法,比如:DFP算法,BFGS算法,L-BFGS算法以及Broyden类算法等。本文主要介绍前两种算法构造近似还塞矩阵。
1、拟牛顿条件
那么,如何构造一个近似海塞矩阵呢?即构造出来的近似海塞矩阵需要满足哪些条件呢?为此,我们先来看下牛顿法中的海塞矩阵是如何推导出来的。
在牛顿法中,首先对函数f(x)在x=xk+1处进行泰勒展开,即:
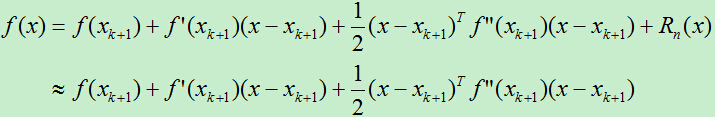
然后对f(x)求偏导:

在牛顿法中,到此步后我们就已经得到了海塞矩阵,然后对f(x)的导数赋值为0,得到x的值。
但是我们这次是为了得到海塞矩阵需要满足的条件,于是我们令x=xk得到:
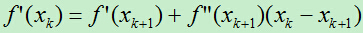
即:
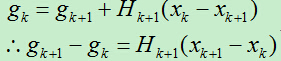
为了简化下面的符号表达式,令:

于是有:
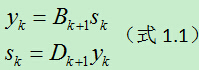
上式中Bk+1为海塞矩阵,Dk+1为海塞矩阵的逆矩阵。
到了此步,我们可以看出海塞矩阵需要满足(式1.1)这个条件。那么在满足此条件的基础上如何构造近似海塞矩阵呢?下面介绍两个方法:DFP算法和BFGS算法。
1、DFP算法
该算法的核心思想在于通过迭代的方法,逐步改善近似海塞矩阵。我们使用D来表示近似海塞矩阵的逆矩阵。其迭代公式为:

该算法最核心的就是每次迭代的海塞矩阵的变化量如何计算?由于海塞矩阵是正定矩阵,所以可以将其变化量设为:
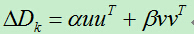
其中向量u,v为待定向量,其维数为:n*1。(n为x的维度)。通过这种方式得到矩阵变化量一定是对称矩阵。
根据(式1.1)有:
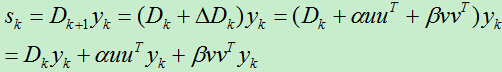
由于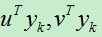 是1*1矩阵,即是一个数,于是我们可以继续转化:
是1*1矩阵,即是一个数,于是我们可以继续转化:
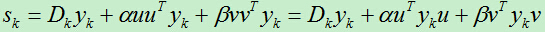
为了简便,我们令:

即:
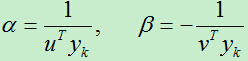
上面两个数中,一个赋1,一个赋-1,这可能是先辈们探索出来的,尤其是-1在后面恰好用到。这大大简化了问题。
于是:

即:
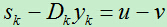
这时,我们再令:
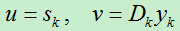
于是有:
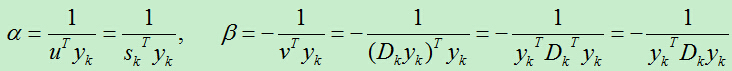
所以,我们可以得到:

DFP算法流程:
1)初始化x=x0,阀值a,并令D0=I,k=0.
2)计算搜索方向:
3)搜索步长 ,使得
,使得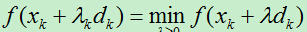 。
。
令:
4)计算 ,若
,若 ,则停止计算,并得到近似解:x=xk+1
,则停止计算,并得到近似解:x=xk+1
5)计算 ,然后计算
,然后计算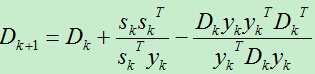
6)令k=k+1,转第2)步。
2、BFGS算法
BFGS算法是用直接逼近海塞矩阵的方式来构造近似海塞矩阵,同样,我们使用迭代的方式来逐步逼近。我们使用B来表示海塞矩阵的近似矩阵,而在DFP算法中我们是直接使用D来构造近似海塞矩阵的逆矩阵。
近似海塞矩阵的迭代公式为:
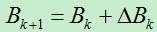
与DFP一样,我们设:
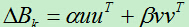
于是有:

令:

于是有:
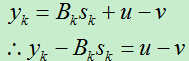
令: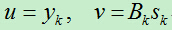
所以得:
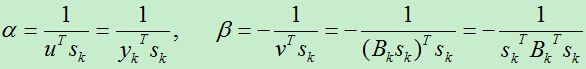
最终,我们得到:
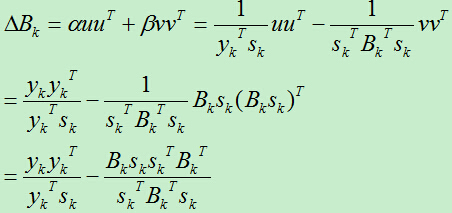
可以证明,若初试矩阵B0是正定的,则迭代过程中的每个矩阵Bk都是正定的。(证明略)
由于上面计算得到的是海塞矩阵的近似矩阵,而在算法中我们需要用到海塞矩阵的逆矩阵,因而我们还需要对已经得到的近似海塞矩阵求逆矩阵。
海塞矩阵的迭代公式为:
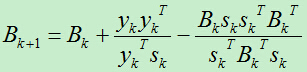
利用Sherman-Morrison公式,我们可以将上式转化成:

通过这种方法,我们就可以更加方便的使用近似海塞矩阵的逆矩阵来进行计算。该算法的流程和DFP算法完全一样,只是将迭代公式略作修改,具体过程可以参考上面的DFP算法。
参考文献:
[1] peghoty, http://blog.csdn.net/itplus/article/details/21896619
[2]李航,统计学习方法。





