提升树算法 详解

提升树是以决策树为基分类器的提升方法，通常使用CART树。针对不同问题的提升树学习算法，主要区别在于使用的损失函数不同。

1）分类问题：指数损失函数。可以使用CART分类树作为AdaBoost的基分类器，此时为分类提升树。

2）回归问题：平方误差损失函数。

3）决策问题：一般损失函数。

 

1、提升树算法

提升树采用线性模型+前向分步算法+CART树（基函数）。提升树的加法模型可表示为：

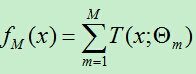（此时树前面并没有权重！！下面有分析）

1）基函数是分类树（二叉分类树）

对于基函数是分类树时，我们使用指数损失函数，此时正是AdaBoost算法的特殊情况，即将AdaBoost算法中的基分类器使用分类树即可。

 

2）基函数是回归树

若基函数是回归树，则使用平方误差损失函数。

我们将回归树的输入空间划分为R1,R2,…,RJ个区域，每个区域的输出分别为：Cj，则回归树可以表示为：

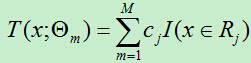
前向分步算法第m步的得到的模型为：

平方误差损失函数为：

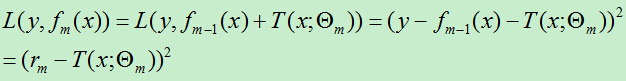
设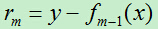：，r_m即为当前模型拟合数据的残差。对回归问题的提升树算法来说，只需简单地拟合当前模型的残差。

因为需要用到上一步的分类器，故而在每轮都需要计算残差，然后遍历可能的切分点，找出平方损失函数最小的切分点将输入划分为两个子集，然后依次类推，直到不能继续划分。

算法过程：

训练集为：T={(x1,y1),(x2,y2),…,(xn,yn)}。

1）初始化：f₀(x)=0

2）下面共进行M轮的迭代，对于第m轮的迭代过程如下：（m=1,2,…,M）

　　A）遍历每个特征的每个可能取值，计算残差：

　　

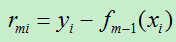
　　B）对于特征的每个可能取值，选择平方损失函数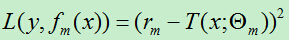最小的切分点，得到树。

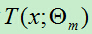　　C）更新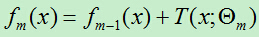

3）最终得到回归问题提升树：

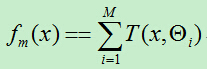
在上面的算法中，并没有在每个基分类器前面加上权值，此算法通过每次减小残差的方式来减小每轮所产生的模型的损失函数，通过这种方式，逐步减小残差值来使得损失函数减小，这样的话最初的模型的损失函数应该最大，那么在最终的线性组合中应该减小它的权重，但是上述算法并没有这样做，而是将每轮产生的模型通过均值或投票的方式来产生最终的结果？？

其实，在每轮的迭代过程中生成的 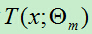并不是一个独立的分类器，它只是对残差的拟合，只有将它添加到前一轮的累加模型中才会对训练集有好的分类或回归效果。

 

3、损失函数最小化方法

         对于最开始提到的三种损失函数，其最小化方法各有不同。当损失函数为下面几种函数时，最小化损失函数的方法如下：

1）指数函数

         当损失函数为指数函数时，比如AdaBoost算法的损失函数是指数函数，这时通过前向分步算法来解决。

         前向分布算法在每轮迭代时，通过将上一轮所生成的模型所产生的损失函数最小化的方法来计算当前模型的参数。

2）平方误差损失函数

         在回归树提升算法中，遍历当前输入样例的可能取值，将每种可能值计算一遍损失函数，最终选择损失函数最小的值。（很原始）

在计算平方损失误差时，可能出现残差项（y-f_m-1(x)），此时可以通过如下方法来进行优化：每一轮迭代是为了减小上一步模型的残差，为了减少残差，每次在残差的负梯度方向建立一个新的模型，这样一步一步的使得残差越来越小。

3）一般损失函数

         对于一般损失函数，可以通过梯度下降的方法来使得损失函数逐步减小，每次向损失函数的负梯度方向移动，直到损失函数值到达谷底。

 

 

 

参考文献：

[1] 李航，统计学习方法。

[2] 林轩田，机器学习技法（coursera）。

[3] leftnoteasy, http://www.cnblogs.com/LeftNotEasy/archive/2011/03/07/1976562.html

[4] w28971023, http://blog.csdn.net/w28971023/article/details/43704775