1135 Is It A Red-Black Tree (30 分)

There is a kind of balanced binary search tree named red-black tree in the data structure. It has the following 5 properties:

• (1) Every node is either red or black.
• (2) The root is black.
• (3) Every leaf (NULL) is black.
• (4) If a node is red, then both its children are black.
• (5) For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.

For example, the tree in Figure 1 is a red-black tree, while the ones in Figure 2 and 3 are not.

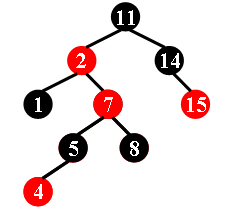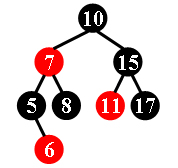Figure 1	Figure 2	Figure 3

For each given binary search tree, you are supposed to tell if it is a legal red-black tree.

Input Specification:

Each input file contains several test cases. The first line gives a positive integer K (≤30) which is the total number of cases. For each case, the first line gives a positive integer N (≤30), the total number of nodes in the binary tree. The second line gives the preorder traversal sequence of the tree. While all the keys in a tree are positive integers, we use negative signs to represent red nodes. All the numbers in a line are separated by a space. The sample input cases correspond to the trees shown in Figure 1, 2 and 3.

Output Specification:

For each test case, print in a line "Yes" if the given tree is a red-black tree, or "No" if not.

Sample Input:

3
9
7 -2 1 5 -4 -11 8 14 -15
9
11 -2 1 -7 5 -4 8 14 -15
8
10 -7 5 -6 8 15 -11 17

Sample Output:

Yes
No
No

代码:

#include <bits/stdc++.h>
using namespace std;
struct node
{
    int val;
    node* l, *r;
};
int v[40];
node* root;

void build(node *now, int val)
{
    int v = now->val;
    if (abs(val) < abs(v))
    {
        if (now->l == NULL)
            now->l = new node(), now->l->val = val;
        else build(now->l, val);
    }
    else
    {
        if (now->r == NULL)
            now->r = new node(), now->r->val = val;
        else build(now->r, val);
    }
}

bool judge(node* x)
{
    if (!x) return true;
    if (x->val < 0)
        if (x->l && x->l->val < 0 || x->r && x->r->val < 0) return false;
    return judge(x->l) && judge(x->r);
}

int cal(node* x)
{
    if (!x) return 0;
    int numl = cal(x->l), numr = cal(x->r);
    if (numl == numr && numl != -1)
        return x->val > 0 ? numl + 1 : numl;
    return -1;
}
int main()
{
    int t; cin >> t;
    while (t--)
    {
        int n; cin >> n;
        for (int i = 1; i <= n; i++)
            cin >> v[i];
        root = new node();
        root->val = v[1], root->l = root->r = NULL;
        for (int i = 2; i <= n; i++)
            build(root, v[i]);
        if (v[1] > 0 && judge(root) && cal(root) != -1) cout << "Yes" << endl;
        else cout << "No" << endl;
    }
}