2020 hdu多校赛 第四场 1009 Imperative Meeting
计数好题,强推。
题意:
给你一棵树,n<=1e6
当给你m个特殊点具体在哪时,你可以找到一个点使这m个点到这个点的总距离最短。
现在问总共C(n,m)种情况的最小距离和。
这种题一般是要固定一个量在计算,显然,我们枚举每个点看他作为最优解时总距离是多少是不可行的,我们考虑每条边做的贡献。
一个比较重要的结论就是如果这条边一侧有X个点,一侧有Y个点,X>Y,那么一定有Y个点要经过这条边,证明显然。
那么我们就要计算一条边一侧有i个特殊点时的贡献:
![]()
我们发现min很难直接计算,所以我们以(m-1/2)为边界将它分为两个相似的式子,
![]()
右侧表示两侧各取m/2个点,显然可以 O ( 1 ) 求出,对于左侧的式子,我们发现他两项是对称的。设 C(s,i)*C(n-s,m-i)*i为g(s), 设 p=(m-1)/2。
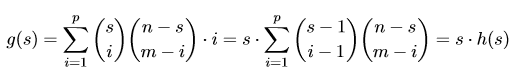
仔细观察这个式子,我们可以把h(s)理解为现在有n-1个不同的盒子,m-1个相同的球,每个盒子最多放一个球,前s-1个盒子最多放p-1个球的方案数。
我们考虑h(s-1)与h(s)的关系。在h(s-1)中成立但在h(s)中不成立当且仅当s-1的位置有一个球,且1~s-2有p-1个球,剩下n-s有m-1-p个球。所以,我们可以通过O(1)递推求出h(s),进而求出f(s)。

1 #include<iostream> 2 #include<cstdlib> 3 #include<cstdio> 4 #include<cstring> 5 #include<algorithm> 6 #include<cmath> 7 #define N 1000005 8 using namespace std; 9 int T,n,m; 10 int fa[N],zz,a[N]; 11 struct ro{ 12 int to,next; 13 }road[N*2]; 14 void build(int x,int y) 15 { 16 zz++; 17 road[zz].to=y; 18 road[zz].next=a[x]; 19 a[x]=zz; 20 } 21 long long ans,tmp; 22 const int p=1e9+7; 23 long long jc[N],ni[N]; 24 long long ksm(long long x,long long z) 25 { 26 long long ans=1; 27 while(z) 28 { 29 if(z&1) ans=ans*x%p; 30 x=x*x%p; 31 z>>=1; 32 } 33 return ans; 34 } 35 long long C(int x,int y) 36 { 37 if(y>x)return 0; 38 if(y<0)return 0; 39 return jc[x]*ni[y]%p*ni[x-y]%p; 40 } 41 int size[N]; 42 long long H[N]; 43 void dfs(int x) 44 { 45 size[x]=1; 46 for(int i=a[x];i;i=road[i].next) 47 { 48 int y=road[i].to; 49 dfs(y); 50 size[x]+=size[y]; 51 int da=size[y]; 52 ans+=(H[da]+H[n-da])%p; 53 ans%=p; 54 if((m&1)==0) ans+=C(size[y],m/2)*C(n-size[y],m/2)%p*(m/2)%p; 55 ans%=p; 56 } 57 58 } 59 int main() 60 { 61 scanf("%d",&T); 62 jc[0]=ni[0]=1; 63 for(int i=1;i<=1000000;i++) 64 { 65 jc[i]=jc[i-1]*i%p; 66 ni[i]=ksm(jc[i],p-2); 67 } 68 while(T--) 69 { 70 scanf("%d%d",&n,&m); 71 zz=0; 72 ans=0; 73 for(int i=1;i<=n;i++) a[i]=size[i]=0; 74 for(int i=2;i<=n;i++) 75 { 76 int x; 77 scanf("%d",&x); 78 build(x,i); 79 fa[i]=x; 80 } 81 tmp=(m-1)/2; 82 if(tmp>=1) H[1]=C(n-1,m-1); 83 else H[1]=0; 84 for(int i=2;i<=n;i++) 85 { 86 H[i]=(H[i-1]-(C(i-2,tmp-1)*C(n-i,m-1-tmp)%p)+p)%p; 87 } 88 for(int i=1;i<=n;i++) H[i]=H[i]*i%p; 89 // for(int i=1;i<=n;i++) cout<<H[i]<<' '; 90 // cout<<endl; 91 dfs(1); 92 printf("%lld\n",ans); 93 } 94 return 0; 95 }



