OpenFOAM——高空腔内的湍流自然对流

本算例来自《ANSYS Fluid Dynamics Verification Manual》中的VMFL052: Turbulent Natural Convection Inside a Tall Cavity

 

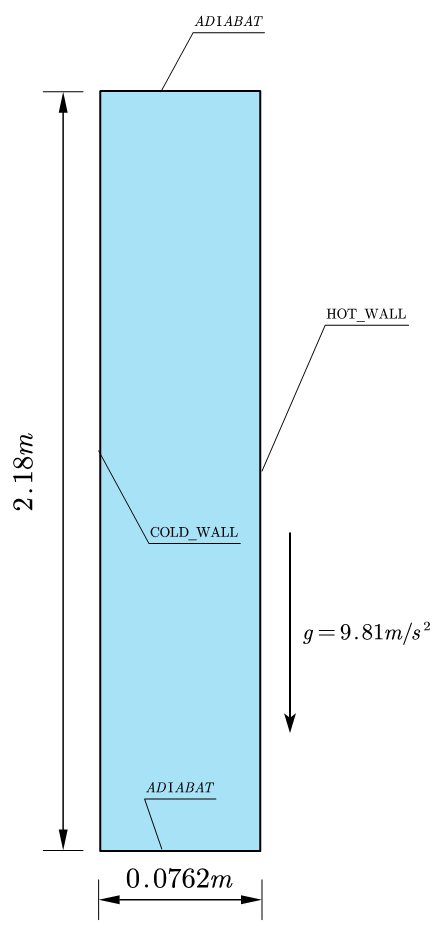
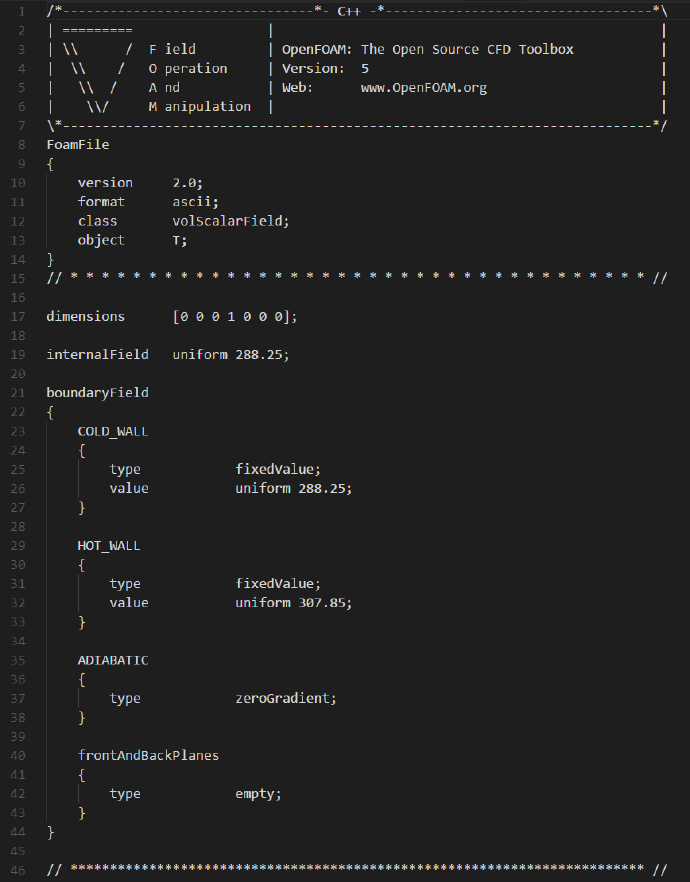
顶部和底部壁面为绝热边界，左侧壁面（COLD_WALL）为288.25K，右侧壁面为（HOT_WALL）为   307.85K

流体的物性参数为：

密度：1.17kg/m³

粘度系数：1.81×10^-5N·s/m²

运动粘度：1.54×10^-5 m²/s

定压比热容：1005J/(kg·K)

导热系数：0.0261W/(m·K)

普朗特数：0.705

 

针对自然对流的方法一般有三种：

①布辛尼斯克(Boussinesq)近似

②不可压理想气体

③密度线性差分方法

本算例采用布辛尼斯克(Boussinesq)近似，布辛尼斯克假设中密度作为常数考虑，浮力作为源项添加，但仅适用于小温差,密度变化小于20%的情况,一般壁面与流体的温差超过200K，布辛尼斯克近似就不适用了。

首先进行建模操作，任何建模软件均可，本算例采用ICEM直接建模，生成网格，然后利用OpenFOAM下转化网格，划分完成的网格局部如下： 

 

网格比较密集，高度方向设置了2000个节点，宽度方向上设置了100个节点，在导出网格的同时，我们对网格进行了缩放。建议在导出网格的时候就缩放网格，避免在后面的操作中，由于忘记缩放网格，导致计算出错

接下来转入OpenFOAM的操作：

首先新建一个文件夹，名字任取，用来作为算例文件夹，本算例中我将该文件夹命名为：Tall_Cavity 

然后进入OpenFOAM的安装目录，将安装目录下的hotRoom算例（我的目录为/opt/openfoam5/tutorials/heatTransfer/buoyantBoussinesqSimpleFoam/hotRoom）下的0文件夹、constant文件夹和system文件夹拷贝到Tall_Cavity文件夹下，然后删除system目录下的blockMeshDict文件，因为我们利用OpenFOAM的命令转化.msh文件为OpenFOAM能接受的网格文件。

然后我们将刚才我们生成的.msh网格拷贝到Tall_Cavity文件夹下。在算例文件夹下打开终端，输入fluentMeshToFoam命令：

  

    我们打开constant文件夹下的transportproperties文件，内容修改如下：

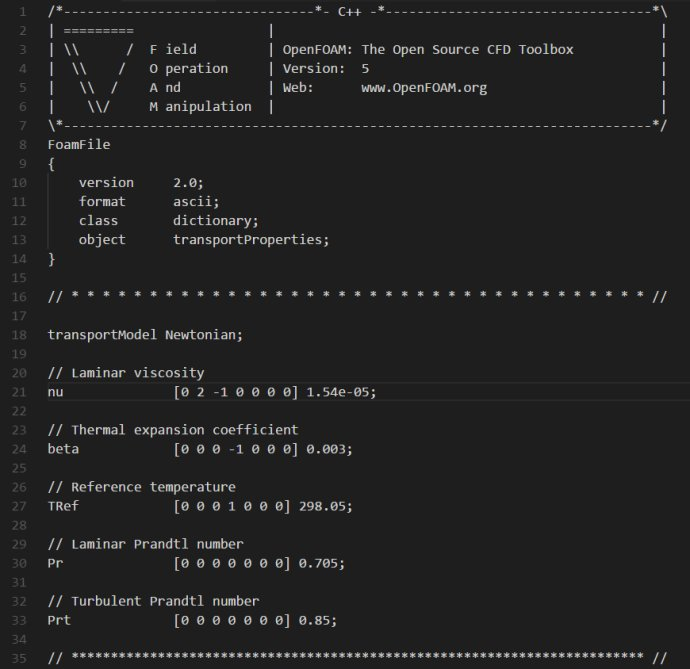
说明一下：

nu表示层流粘度，这里根据上面的物性填写1.81e-05即可，注意下量纲，这里是运动粘度，需要用动力粘度除以密度

beta表示热膨胀系数，一般取为三百分之一（0.003）

Tref表示参考温度，这里我们取为两壁面温度的算术平均值，这里填写298.05

Pr表示普朗特数，这里我们根据上面的物性参数填写0.705

最后的湍流普朗特数根据实验得到，一般不用改动

 接下来，修改turbulenceProperties文件的内容如下：

 

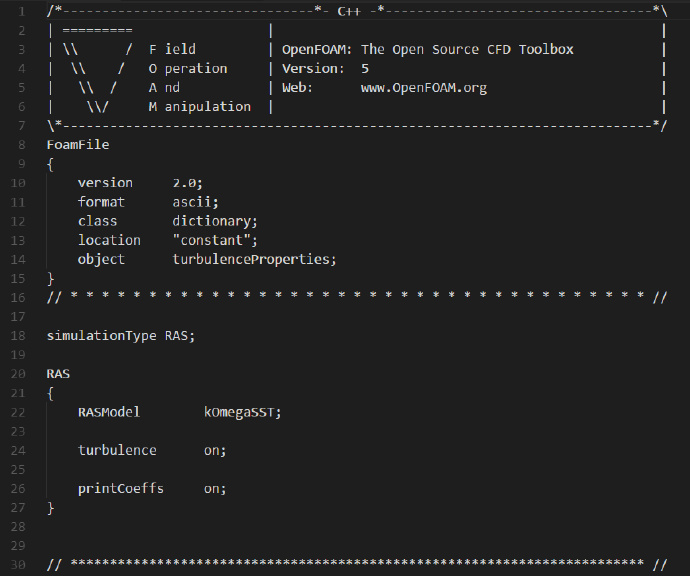
本算例我们采用k-ωSST湍流模型来进行计算（后面需要在0文件夹下添加omega文件）

g文件无需修改，默认设置超Y轴方向重力，重力加速度为9.81m/s²

然后对初始边界条件进行设置，下面转入0文件夹下进行操作：

删除不需要的文件

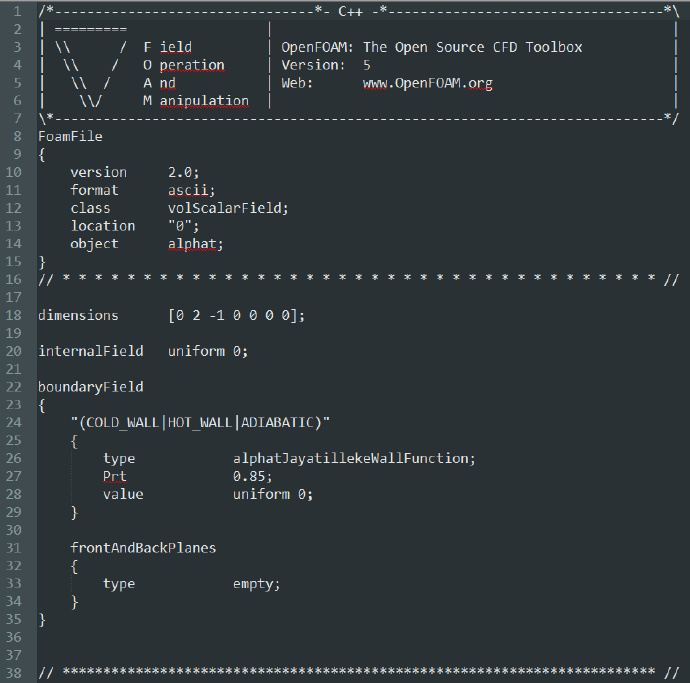
     alpha文件当中的内容如下：

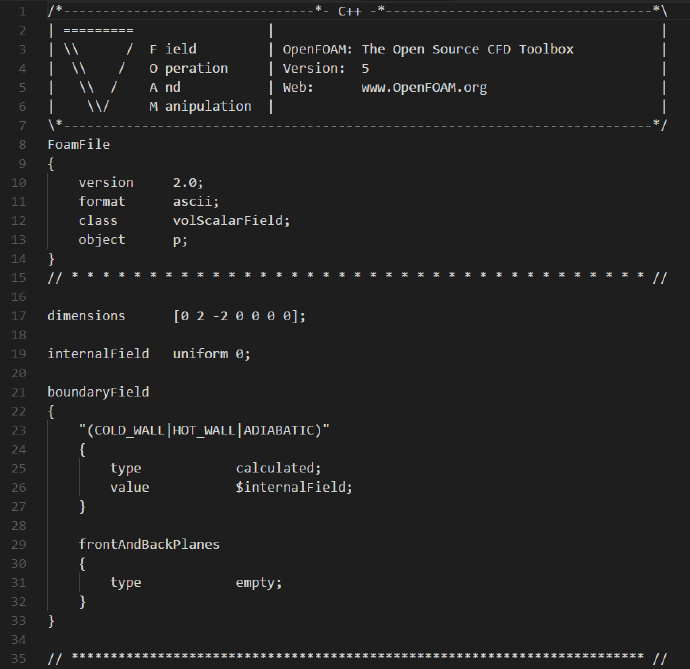
           p文件当中的内容如下：

           p_rgh文件当中内容如下： 

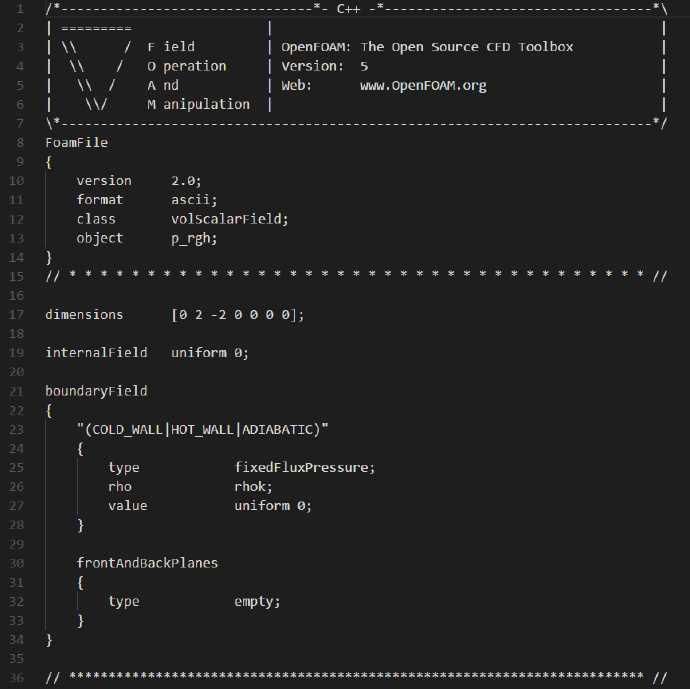
           U文件当中的内容如下：

 

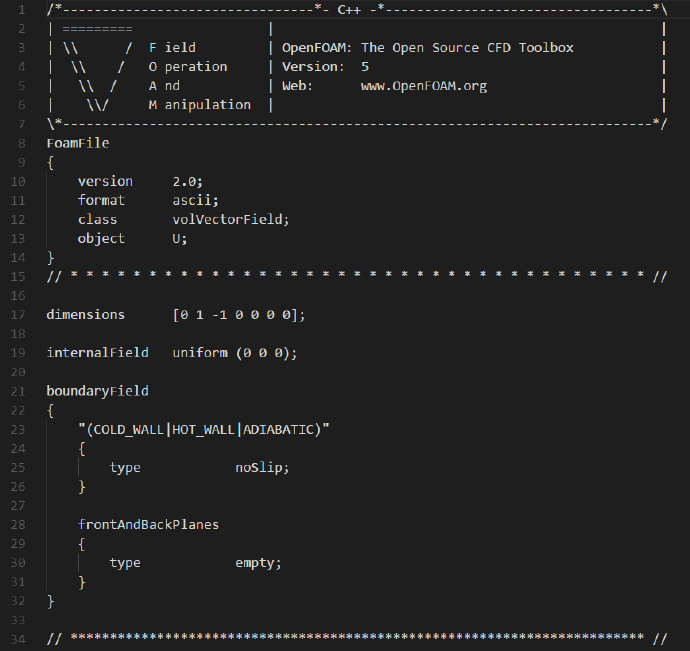
将T.org的文件名修改为T,当中的内容如下： 

 

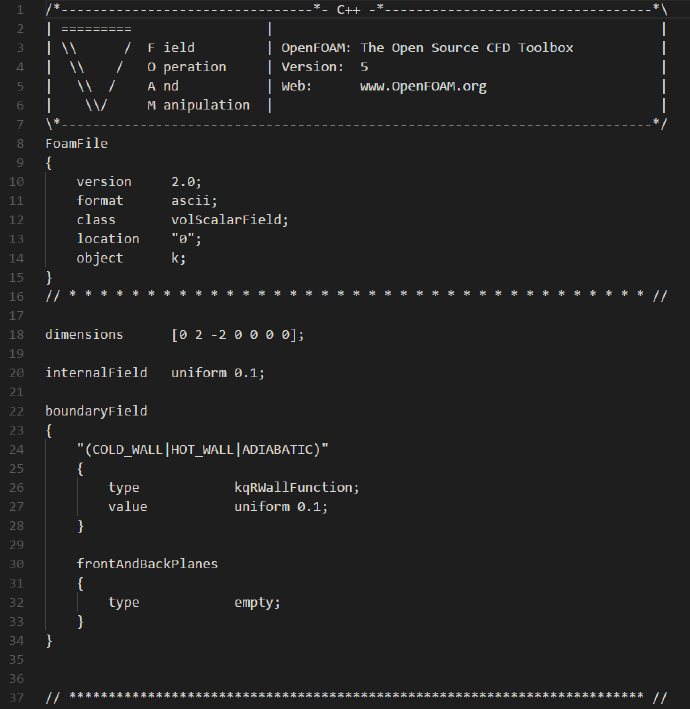
k文件当中的内容如下： 

 

说明一下：

在壁面处，k应该为0。这里我们使用了壁面函数。

k表示湍动能，计算公式为：

 

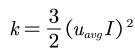
其中：u_avg为平均速度

      I为湍流强度

    湍流强度的计算公式为：

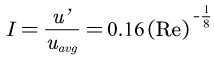
    式中：Re表示雷诺数

    为何一般初始湍流强度设置为5%，可参考Launder B E, Spalding D B. The numerical computation of turbulent flow Computer methods in applied mechanics and engineering[J]. Надійшла до редакції 04.12. 2009 р, 1974.

MLA(文章链接：http://www.sciencedirect.com/science/article/pii/0045782574900292)

omega文件当中的内容如下：

 

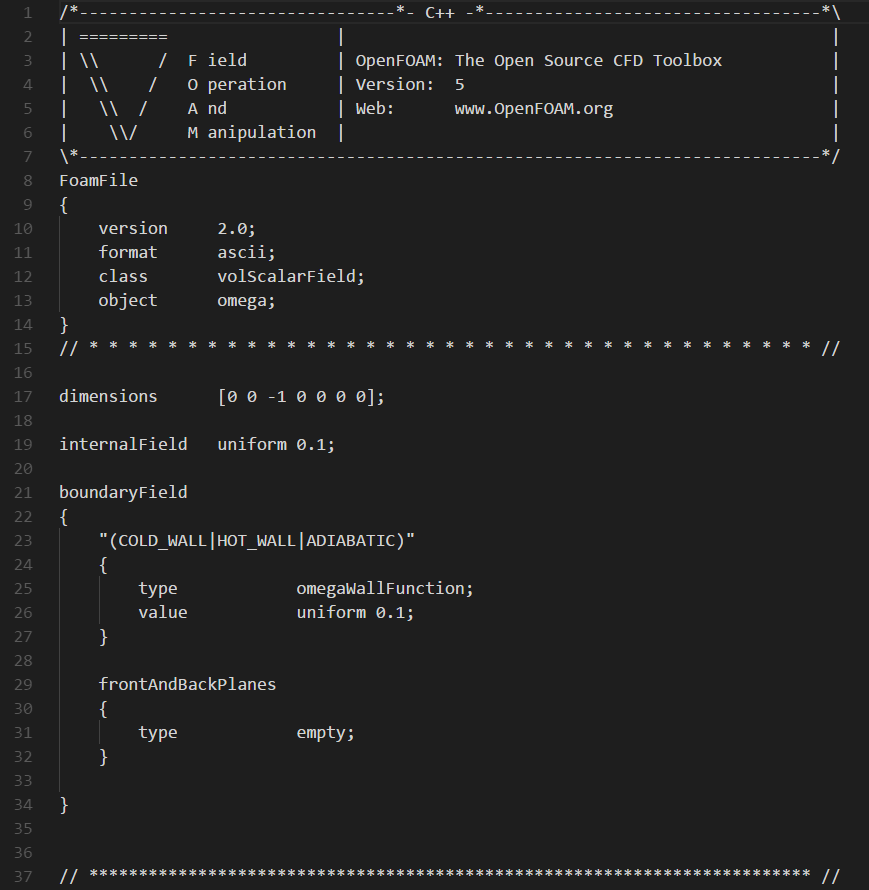
说明一下：

omega表示比耗散率，计算公式如下：

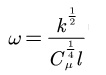
式中：C_μ为0.09

      k为湍动能

      l为特征长度

nut文件内容如下：

 

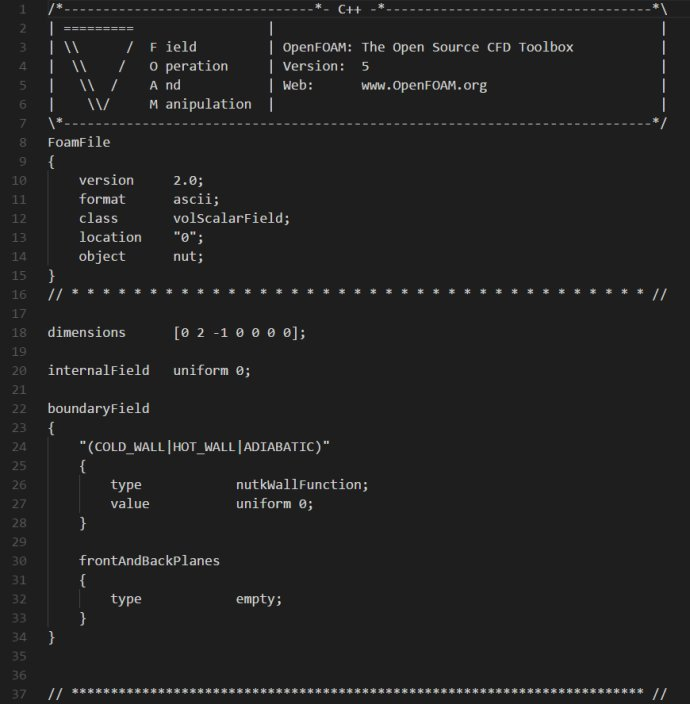
说明一下：

nut表示湍流粘度，其计算公式为：

 

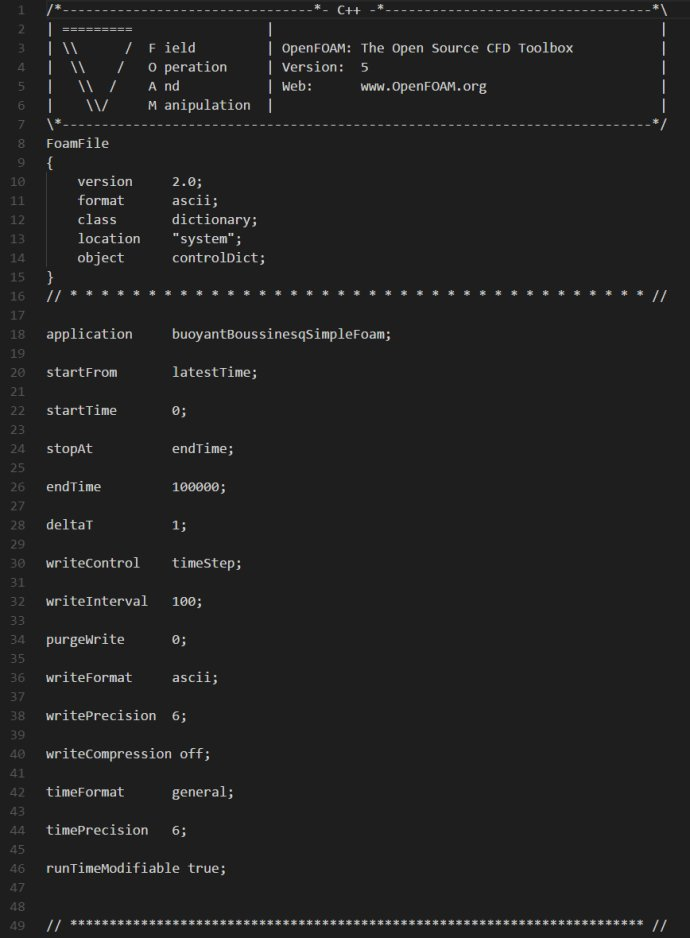
接着我们设置controlDict文件

 

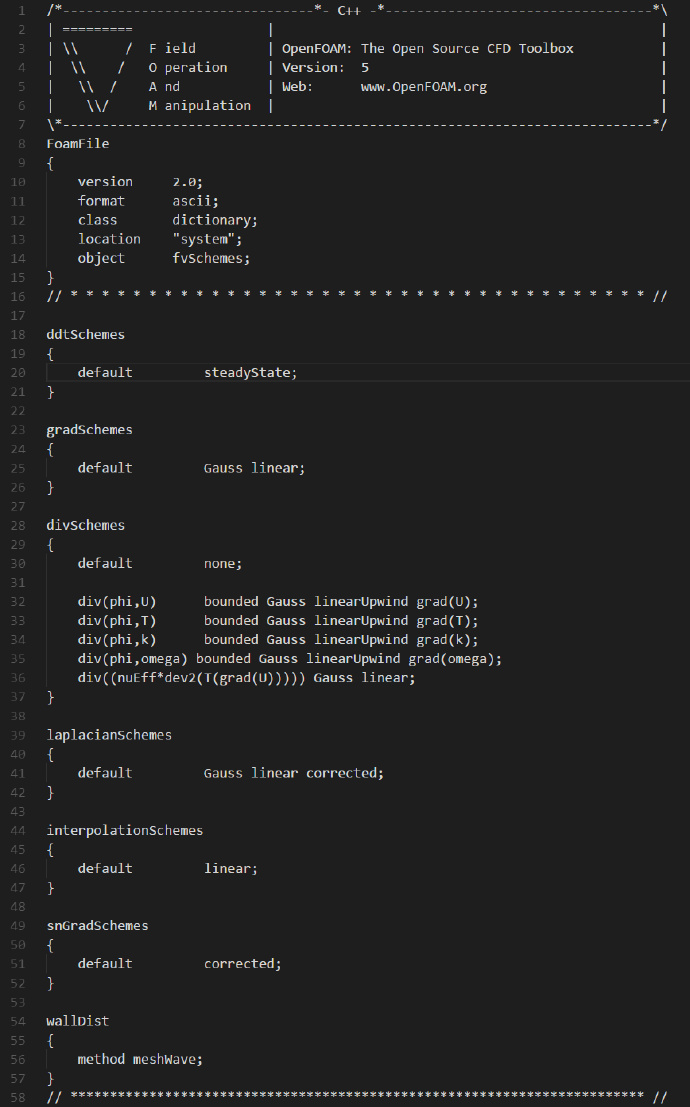
fvSchemes文件修改如下：

 

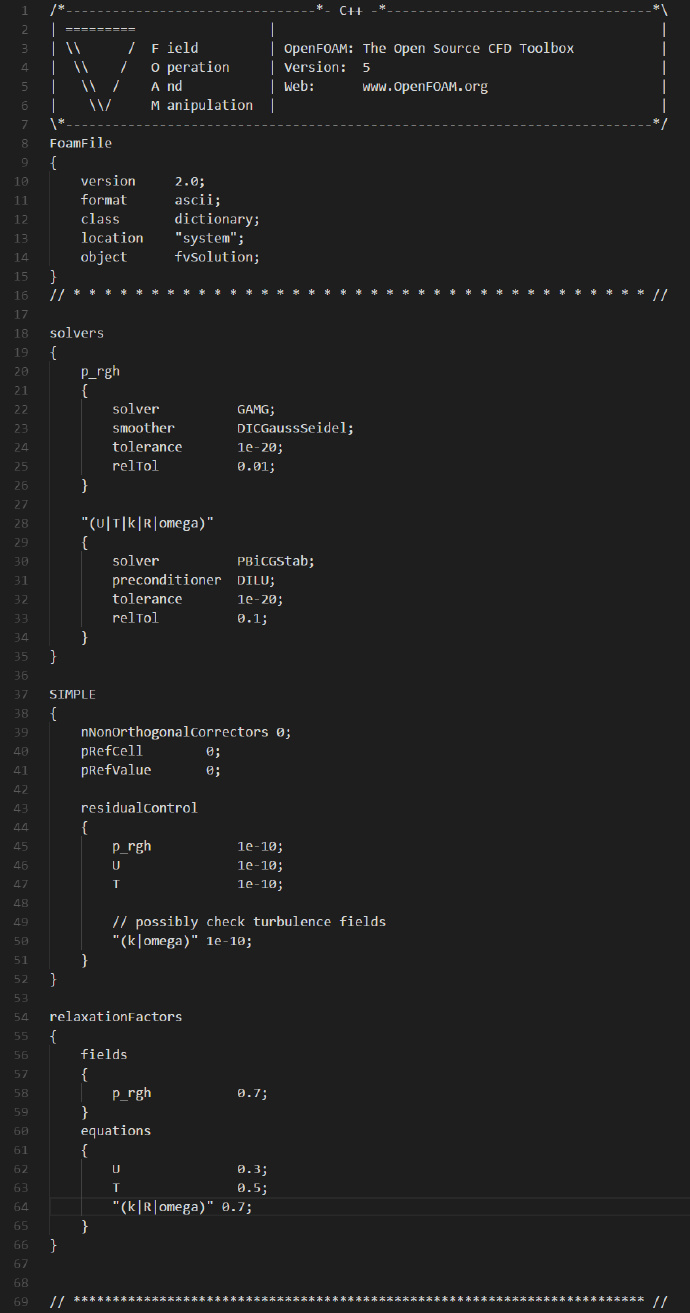
fvSolution文件修改如下：

 

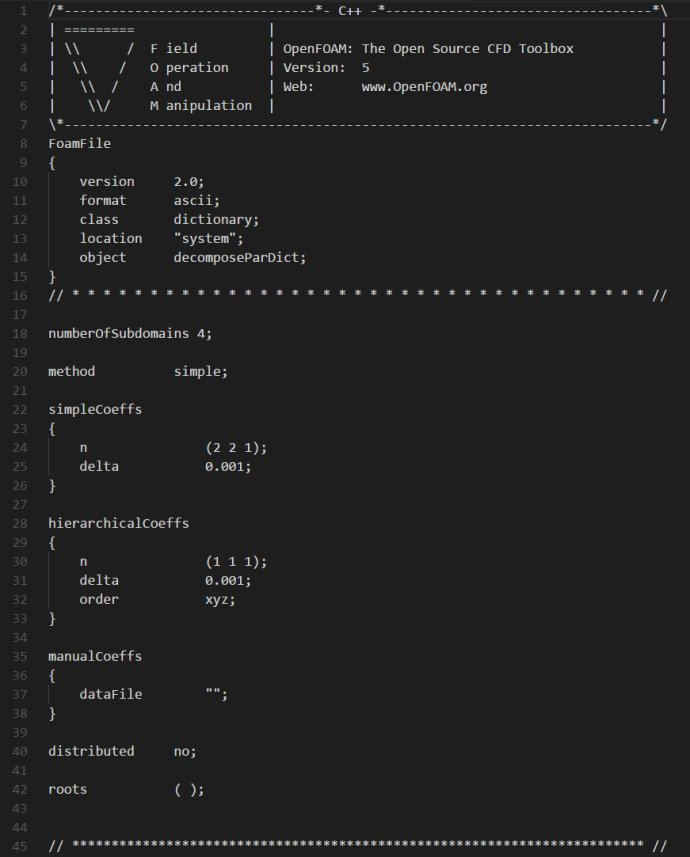
为了加快计算速度，我们进行并行计算，回到算例文件夹下的system目录，新建一个decomposeParDict字典，其中的内容：

 

打开终端，输入decomposePar进行分块

 

 

由于我安装了PyFoam来实时输出残差，所以在终端中输入pyFoamPlotRunner.py --clear mpirun -np 4 buoyantBoussinesqSimpleFoam -parallel开始计算：

 

等到计算结束

 

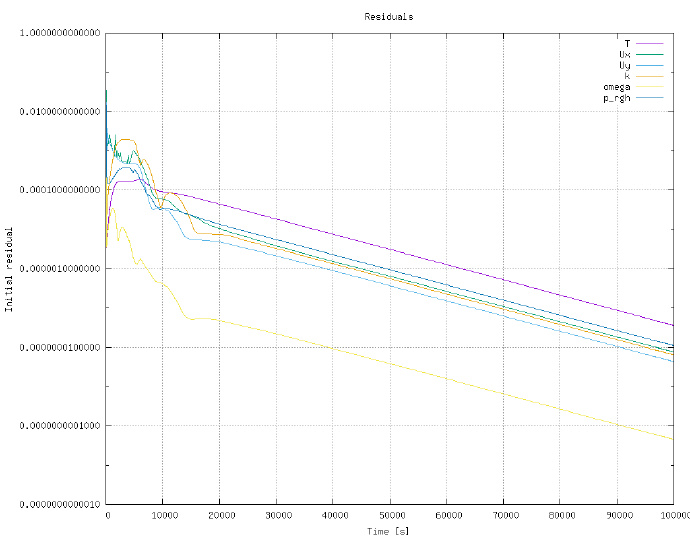
将计算结果导入paraview里面进行处理 

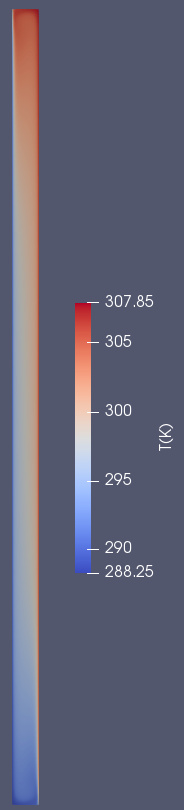
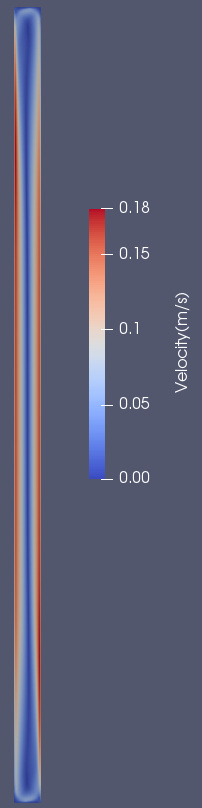
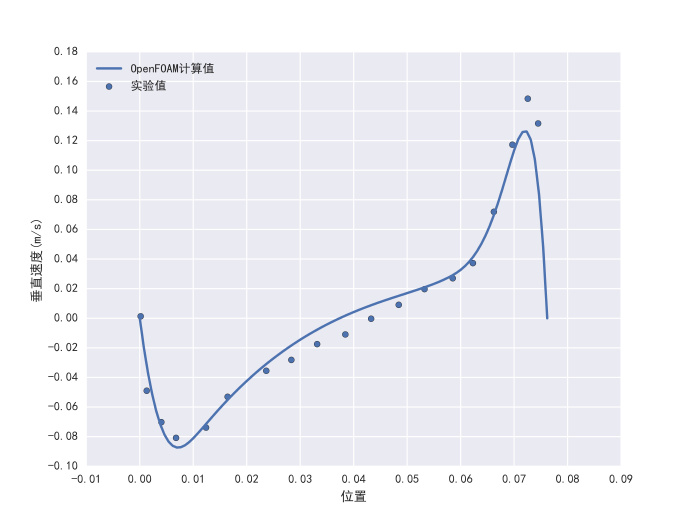
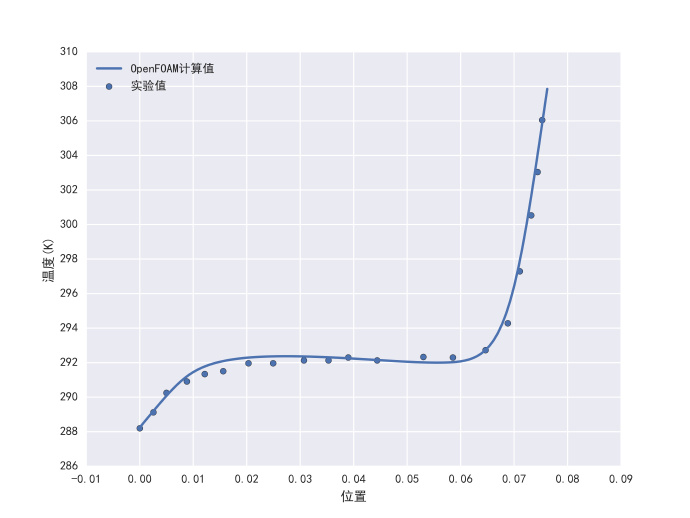
计算结果与实验数据对比：