UDS的使用

我们通过对导热微分方程式的求解，并与Fluent自己的求解结果进行对比，介绍一下Fluent当中UDS（自定义标量）的具体使用方法。

首先Fluent当中的UDS主要针对下面这样形式的方程：

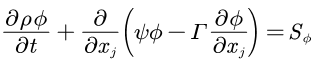
其中：

φ——表示自定义求解的变量

t——表示时间

Γ——表示扩散系数

Ψ——表示对流系数

S_φ——表示源项

完整的导热微分方程式对应上面的标准形式为(未考虑对流项)：

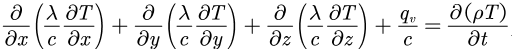
其中：

T——表示温度

t——表示时间

ρ——表示密度

c——表示比热容

q_V——表示内热源

这里我们的自定义标量就是对应这里的温度T，我们将UDS求解的结果与用Fluent求解的结果进行对比

为了简化问题我们这里采用二维模型

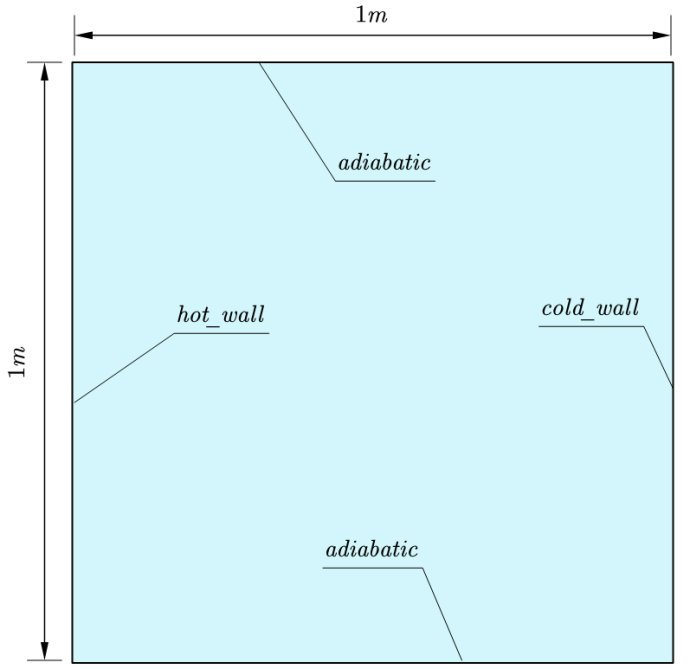
二维网格如下：

我们首先考虑二维稳态无内热源只考虑扩散的情况，方程简化为下面的形式：

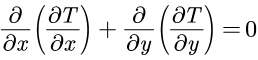
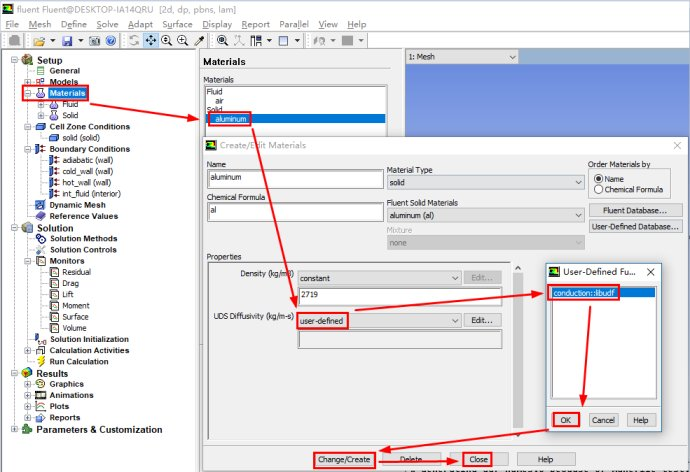
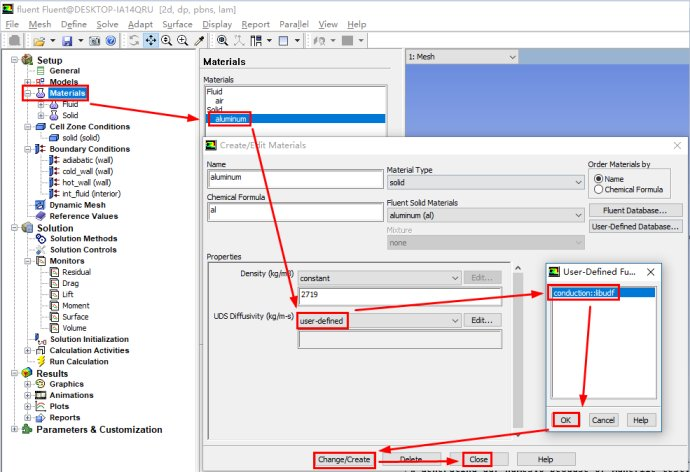
　　我们只需要定义自定义标量当中扩散系数 (即导热系数λ)，我们编写下面简单的代码来指定扩散系数为常数1.0： 

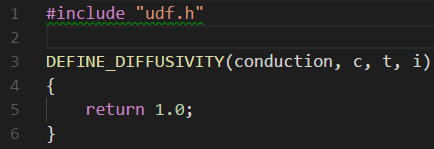
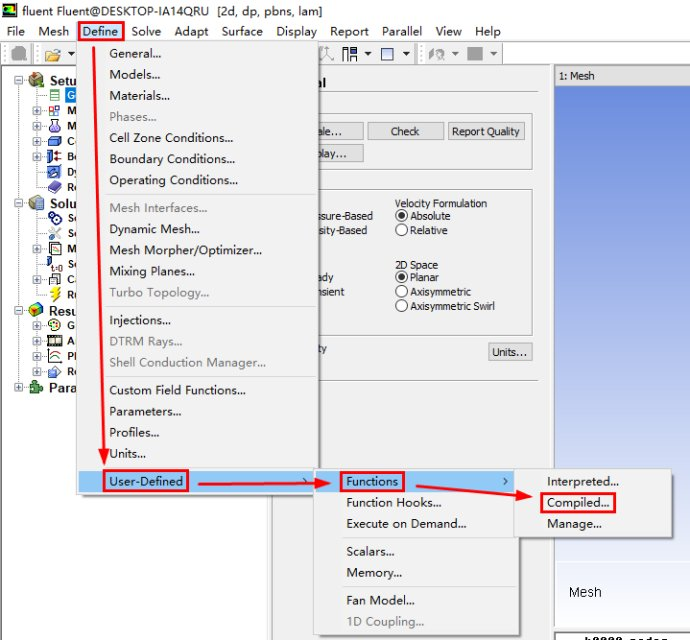
然后我们转入Fluent当中进行操作

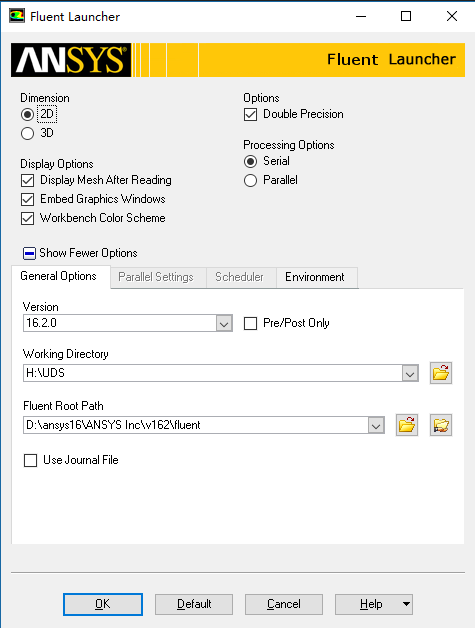
首先我们打开Fluent

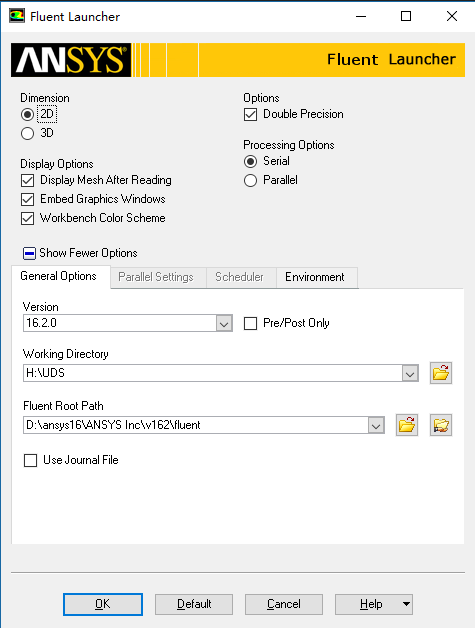
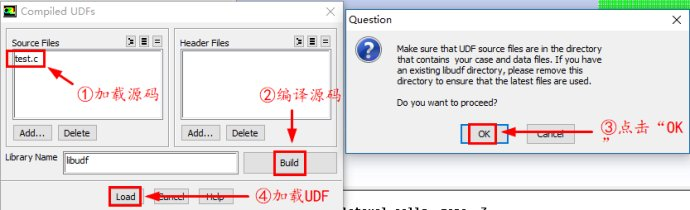
加载网格，然后加载上面的UDF

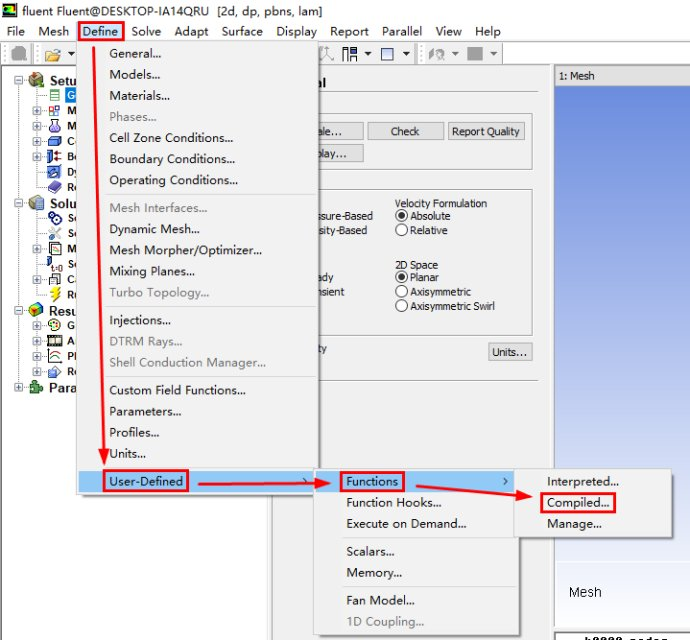
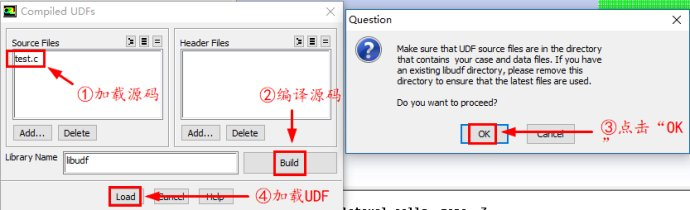
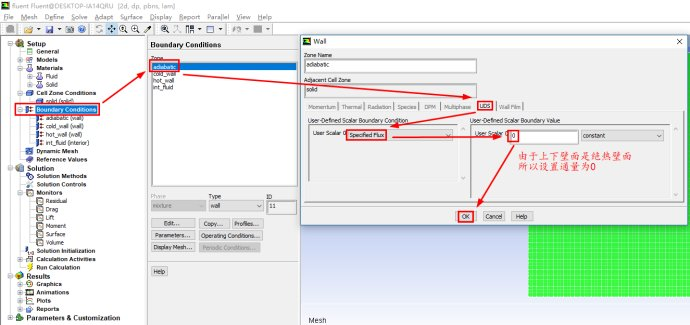
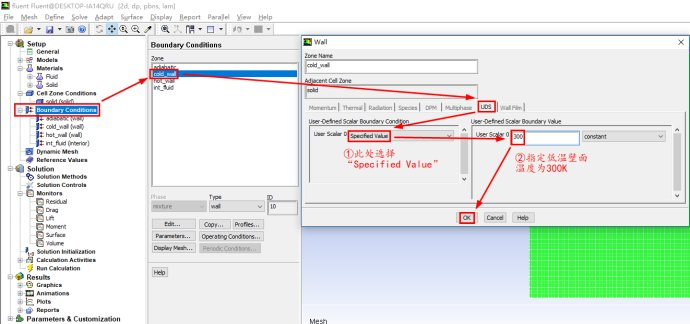
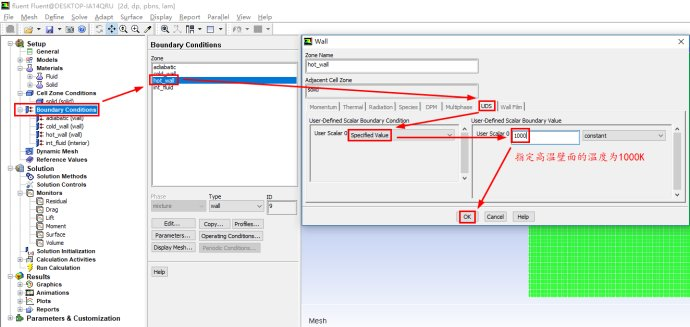
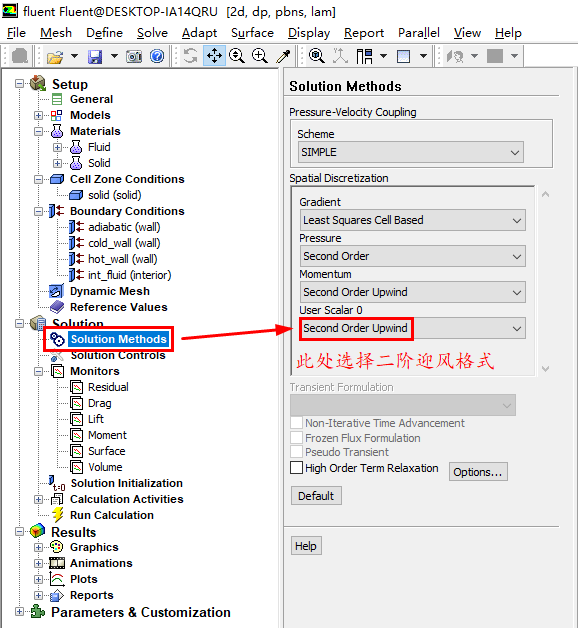
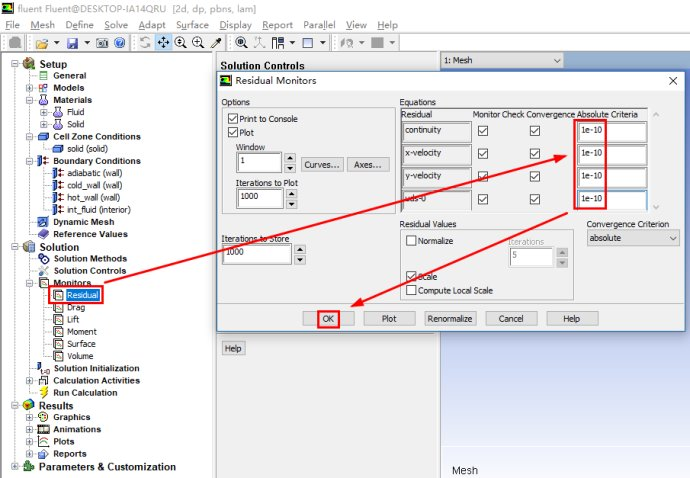
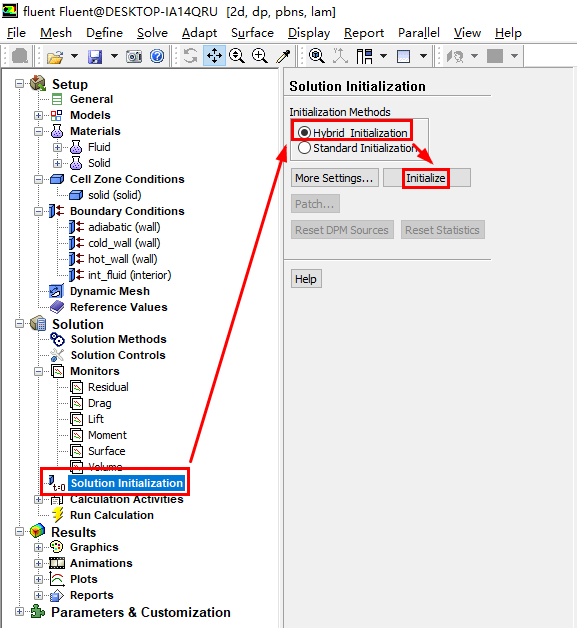
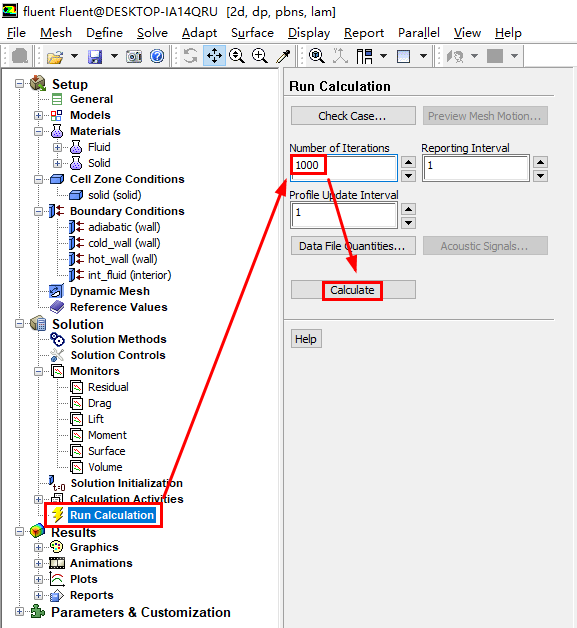
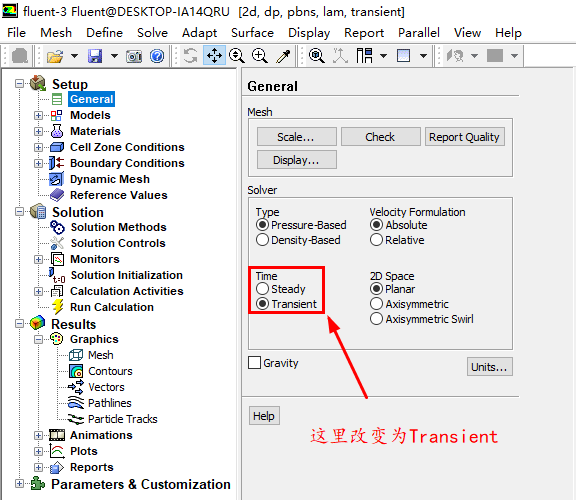
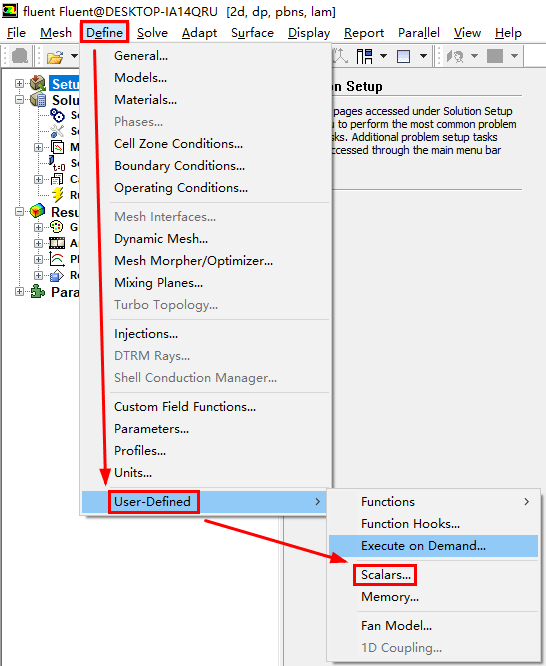
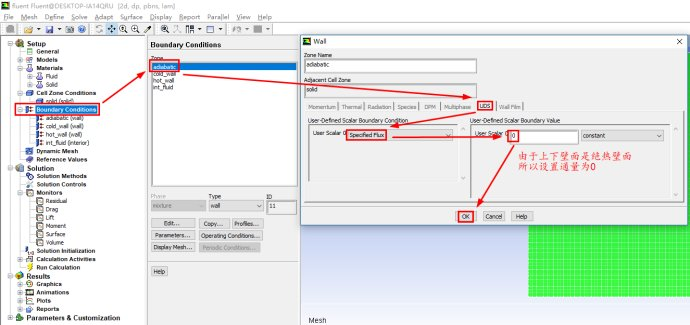
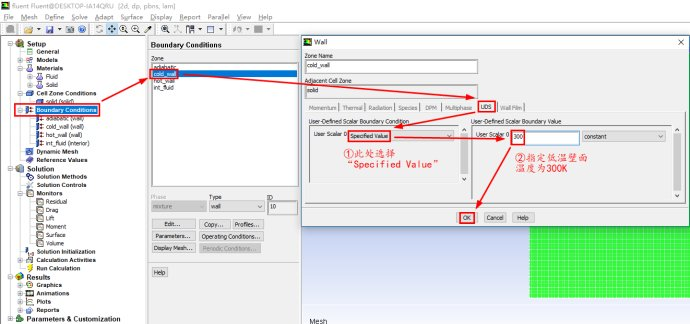
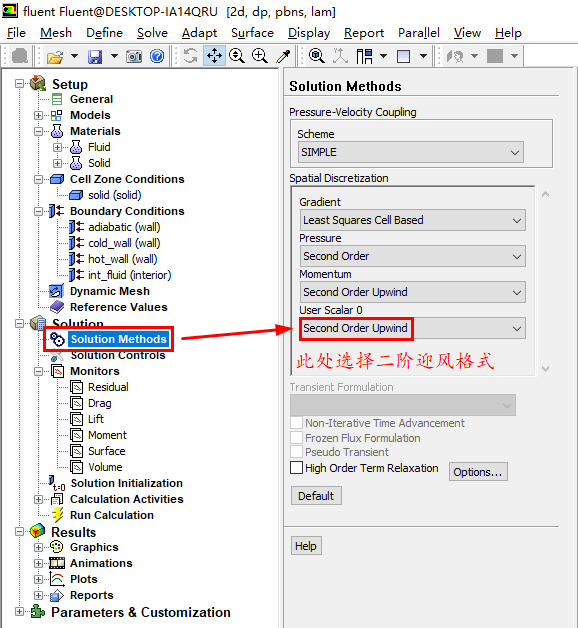
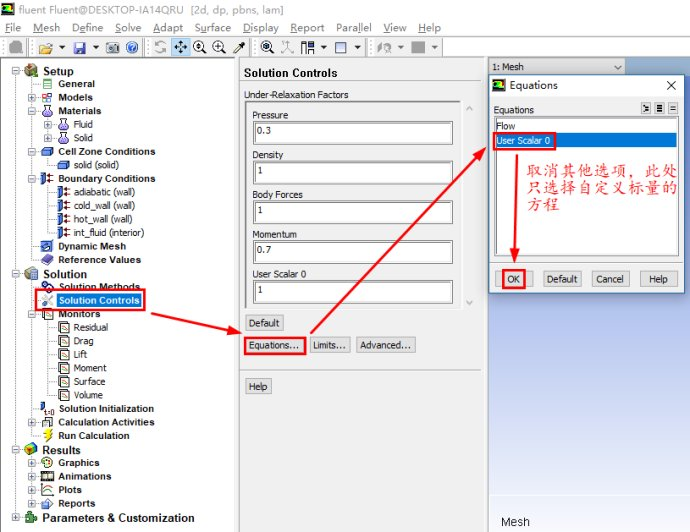
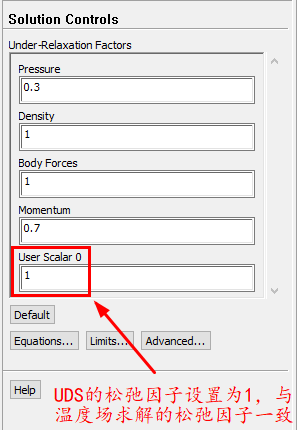
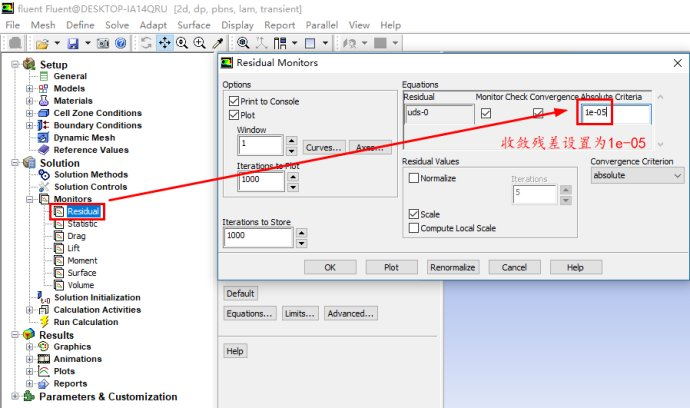
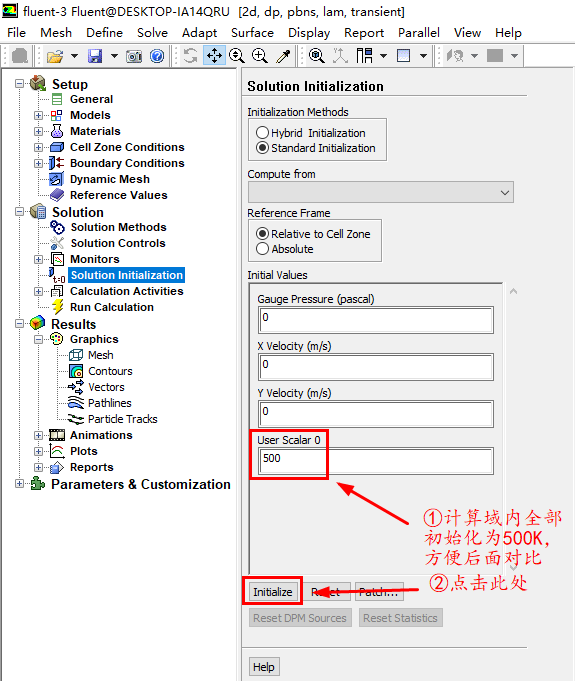
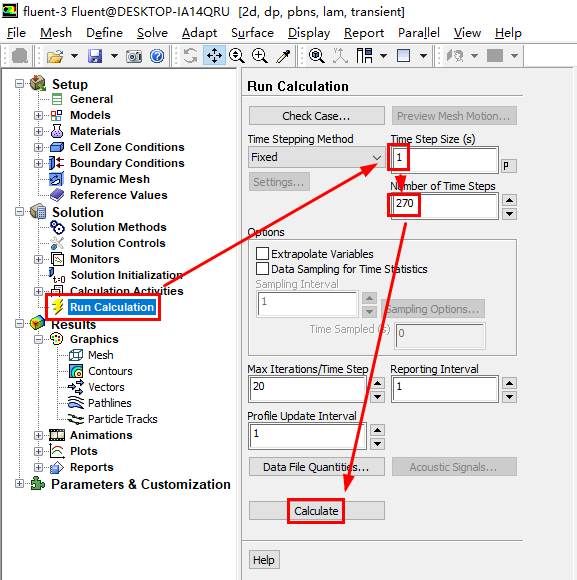
进行相关的求解设置

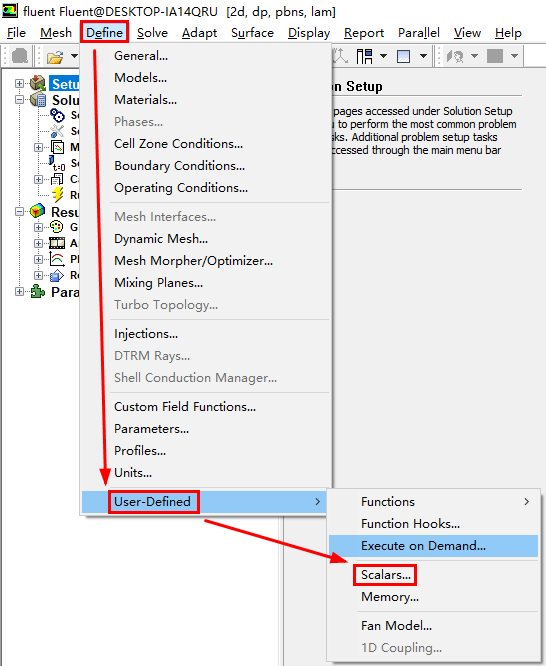
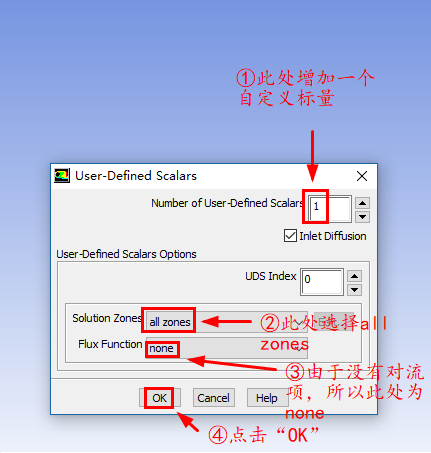
说明一下：

Number of User-Defined Scalars用于指定自定义标量的个数，本示例只有一个自定义标量，所以此处为1

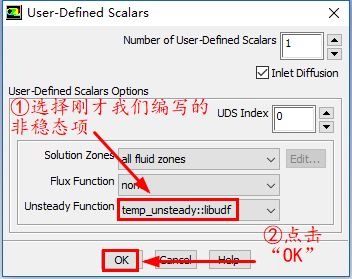
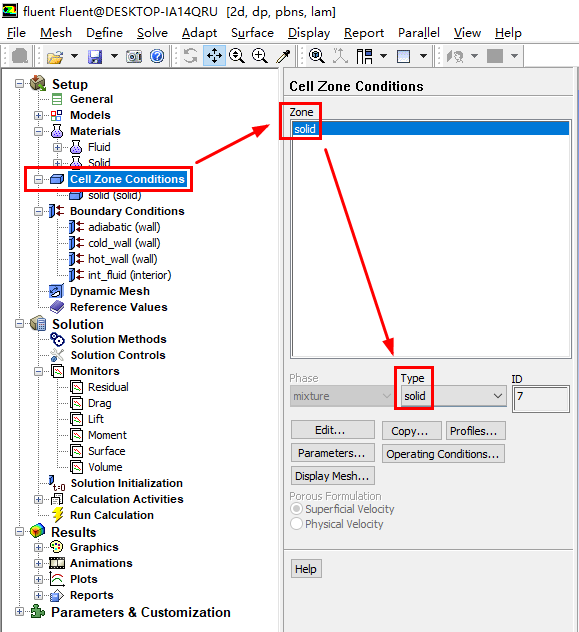
Solution Zones选项可以指定我们求解的区域，我们可以仅求解流体域（all fluid zones），固体域（all solid zones）或者所有的计算域（同时包含流体和固体域，all zones），我们也可以指定求解特定的区域（selected zones）

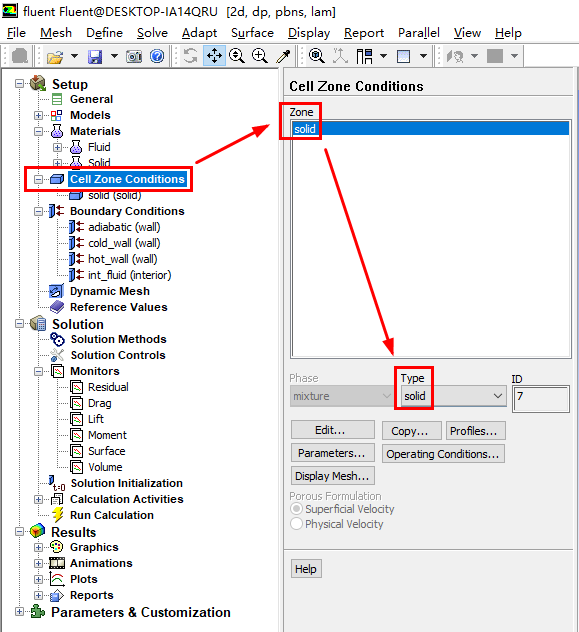
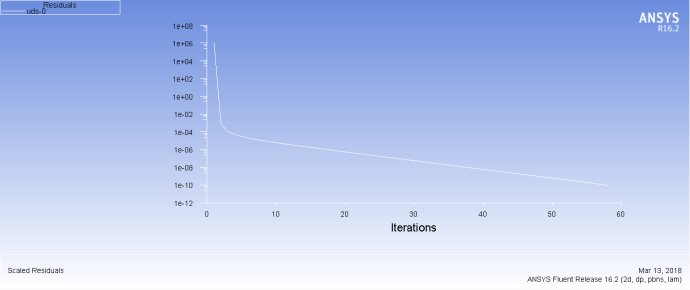
接下来我们考虑二维瞬态无内热源的情况，方程简化为下面的形式：

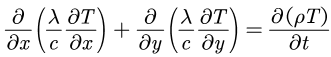
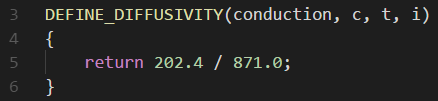
这里扩散系数为：

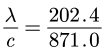
这里我们导热系数取为λ=202.4W/(m·K)，c=871.0J/(kg·K)

针对扩散系数我们编写如下的代码：

而针对瞬态项，根据Fluent的UDF手册

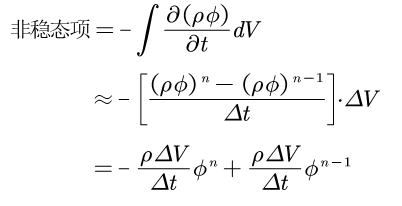
其中：

 而针对导热微分方程，只需要把上面的φ换为温度T

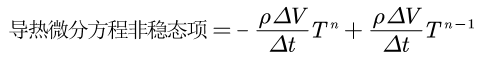
我们对非稳态项编写如下代码：

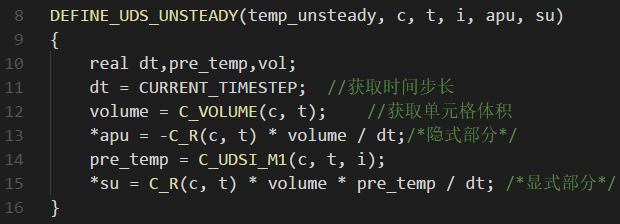
完整代码如下：

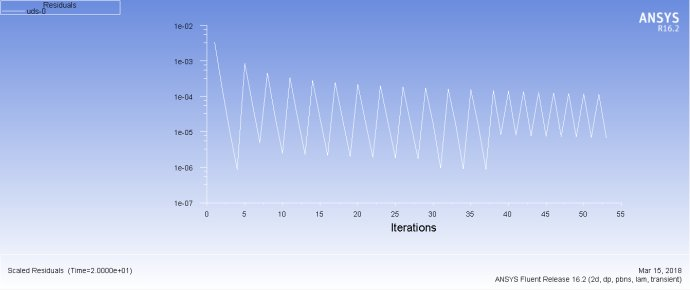
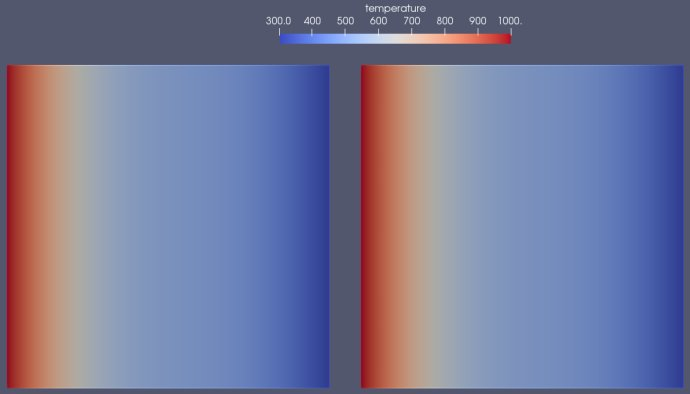
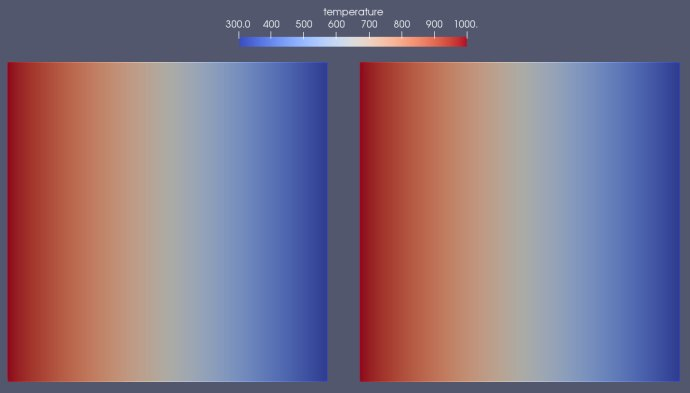
在270s时结果对比，可以看出我们编写的求解代码与Fluent求解的温度场是一致的

对于源项的考虑和我们一般的考虑源项是一样的，就不再赘述了