数学期望

离散型
\( 如果随机变量只取得有限个值或无穷能按一定次序一一列出，其值域为一个或若干个有限或无限区间，这样的随机变量称为离散型随机变量。 \\ 离散型随机变量的一切可能的取值x_i与对应的概率p(x_i)乘积之和称为该离散型随机变量的数学期望(若该求和绝对收敛），记为E(x)。 \\ 它是简单算术平均的一种推广，类似加权平均。 \)
公式
\(离散型随机变量X的取值为X_1,X_2,X_3,...,X_n，p(X_1),p(X_2),p(X_3),...,p(X_n)为X对应取值的概率，可理解为数据X_1,X_2, \\ X_3,...,X_n出现的频率f(X_i)，则： \\ E(X)=X_1\times p(X_1)+X_2*p(X_2)+...+X_n\times p(X_n)=X_1\times f(X_1)+X_2\times f(X_2)+...+X_n\times f(X_n) \)

\[\downdownarrows \\ E(X)=\sum_{k=1}^{\infty}x_kp_k \]

连续型
\( 设连续性随机变量X的概率密度函数为f(x)，若积分绝对收敛，则称积分的值\int_{-\infty}^{\infty}xf(x)dx为随机变量的数学期望，记为E(X)。 \)

\[E(X)=\int_{-\infty}^{\infty}xf(x)dx \]

\( 若随机变量X的分布函数F(x)可表示成一个非负可积函数f(x)的积分，则称X为连续性随机变量，f(x)称为X的概率密度函数（分布密 \\ 度函数）。 \\ 数学期望E(X)完全由随机变量X的概率分布所确定。若X服从某一分布，也称E(X)是这一分布的数学期望。 \)
定理
\( 若随机变量Y=g(x)符合函数，且\int_{-\infty}^{\infty}g(x)f(x)dx绝对收敛，则有： \)

\[\int_{-\infty}^{\infty}g(x)f(x)dx \]

\( 该定理的意义在于：我们求E(Y)时不需要算出Y的分布律或者概率分布，只要利用X的分布律或概率密度即可。 \\ 上述定理还可以推广到两个或以上随机变量的函数情况。 \\ 设Z是随机变量X、Y的函数Z=g(X,Y)（g是连续函数），Z是一个一维随机变量，二维随机变量（X，Y）的概率密度为f(x,y)，则有： \)

\[E(Z)=E[g(X,Y)]=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}g(x,y)f(x,y)dxdy \]

区别
\( 离散型随机变量与连续型随机变量都是由随机变量取值范围(取值)确定。 \\ 变量取值只能取离散型的自然数，就是离散型随机变量。例如，一次掷20个硬币，k个硬币正面朝上，k是随机变量。k的取值只能是自然数0， \\ 1，2，…，20，而不能取小数3.5、无理数\sqrt{20}，因而k是离散型随机变量。 \\ 如果变量可以在某个区间内取任一实数，即变量的取值可以是连续的，这随机变量就称为连续型随机变量。例如，公共汽车每15分钟一班， \\ 某人在站台等车时间x是个随机变量，x的取值范围是[0,15），它是一个区间，从理论上说在这个区间内可取任一实数3.5、无理数\sqrt{20}等，因而称这随机变量是连续型随机变量。 \)
性质
\( 设C为一个常数，X和Y是两个随机变量。以下是数学期望的重要性质： \\ 1.E(C)=C \\ 2.E(CX)=CE(X) \\ 3.E(X+Y)=E(X)+E(Y) \\ 4.当X和Y相互独立时，E(XY)=E(X)E(Y) \\ 性质3和性质4可以推到到任意有限个相互独立的随机变量之和或之积的情况。 \\ 证明：这里只对连续性随机变量的情况加以证明，对离散型的证明只要将证明中的积分\int改为和式\sum即可。 \\ 1.永远都只能取C，常数C的平均数还是它本身。 \\ 2.E(X)=\int_{-\infty}^{\infty}cxf(x)dx=c\int_{-\infty}^{\infty}xf(x)dx \\ 3.设二维随机变量(X,Y)的概率密度函数为f(x,y)。 \)

\[E(X+Y)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}(x+y)f(x,y)dxdy=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}xf(x,y)dxdy+\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}yf(x,y)dxdy \\ =E(X)+E(Y) \]

\( 4.若X和Y相互独立，其边缘概率密度函数为f_X(x),f_Y(y)，有f(x,y)=f_X(x)f_Y(y) \)

\[E(XY)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}xyf(x,y)dxdy=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}xyf_X(x)dxdyf_Y(y)dxdy=[\int_{-\infty}^{\infty}xf_X(x)dx][\int_{-\infty}^{\infty}yf_Y(y)dy]=E(X)E(Y) \]

例题
NOIP2018提高组初赛试题第7题
\( 在一条长度为 1 的线段上随机取两个点，则以这两个点为端点的线段的期望长度是（ ）。 \)

\[A. \frac{1}{2}\ \ \ \ \ \ B. \frac{1}{3}\ \ \ \ \ \ \ C. \frac{2}{3}\ \ \ \ \ \ \ D. \frac{3}{5} \]

解析
\( 设该线段在数轴上为[0,1] \\ 设第一个点坐标为x,则第二个点与它的期望距离为 \)

\[\frac{x\times x+(1-x)\times(1-x)}{2\times1}=x^2-x+\frac{1}{2} \]

\( (如图) \)

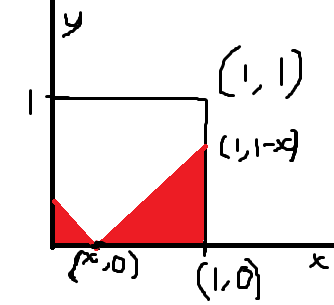
\( 由于x取遍[0,1]两点期望距离为： \)

\[\int_0^1(x^2-x+\frac{1}{2})dx=\frac{1}{3} \\ 故选B。 \]

NOIP2018提高组初赛第九题
\( 假设一台抽奖机中有红、蓝两色的球，任意时刻按下抽奖按钮，都会等概率 获得红球或蓝球之一。有足够多的人每人都用这台抽奖机抽奖， \\ 假如他们的策略均为：抽中蓝球则继续抽球，抽中红球则停止。最后每个人都把自己获得的所有球放到一个大箱子里，最终大箱子里 \\ 的红球与蓝球的比例接近于（ ）。 \)

\[A.1:2\ \ \ \ \ B.2:1\ \ \ \ \ C.1:3\ \ \ \ \ D.1:1 \]

\( 答案：D \\ 解析：一个人在第k轮可以得到的红球期望数量为：\frac{1}{2^k}。 \\ 又因为： \)

\[\sum_{k=1}^{\infty}\frac{1}{2^k}=1 \]

\( 所以每个人得到红球期望数量为1，而得到蓝球数量必定为1，所以1:1。 \\ 图解： \)

\( 由图已知： \\ 红球和黑球数学期望相等，也故1:1。 \)
最后一点

\[我打字也不容易...(Q_AQ)-(T_AT)...点个赞再走吧Q_AQ \]