面试题:找出出现次数超过1/2和1/3的数
要求:时间复杂度为O(n),空间复杂度为O(1)
1、找出次数超过1/2的数
遍历数组num,每次删除两个不同的数,最后剩下的数字便是所求,因为个数超过一半的数字是不会被消除完的。
比如:1 2 1 1 3
- 第一步:删掉1,2,剩1 1 3
- 第二步:因为1 1相同,只保留一个到候选集,剩1 3
- 删掉1 3,候选集里的数字1即为所求。
编程思路:
- 定义candidate:用于临时存储数据,初始化为num[0];定义count:用于表示当前数的出现次数,初始化为1
- 如果下一个数与之前的candidate相同,则count+1
- 否则,count-1
- 出现count=0时,以当前数替代candidate,count=1
- 直到遍历完所有数为止
比如:num={1 ,2,2,1,1,3,1}
- 开始时,candidate=num[0]=1,count=1
- 遍历到num[1]=2,不同数,count-1=0(相当于删除了1 2)
- 遍历到num[2]=2,因为count=0,替换修改candidate=2,count=1(删除完后从下一个数开始遍历,继续寻找与它不同的数字并删除)
- 遍历到num[3]=1,不同数,count-1=0 (删除了2 1)
- 遍历到num[4]=1,因为count=0,替换修改candidate=1,count=1
- 遍历到num[5]=3,count-1=0
- 遍历到num[6]=1,修改candidate=1,count=1
- 遍历完毕,所求数字为1。
代码示例:
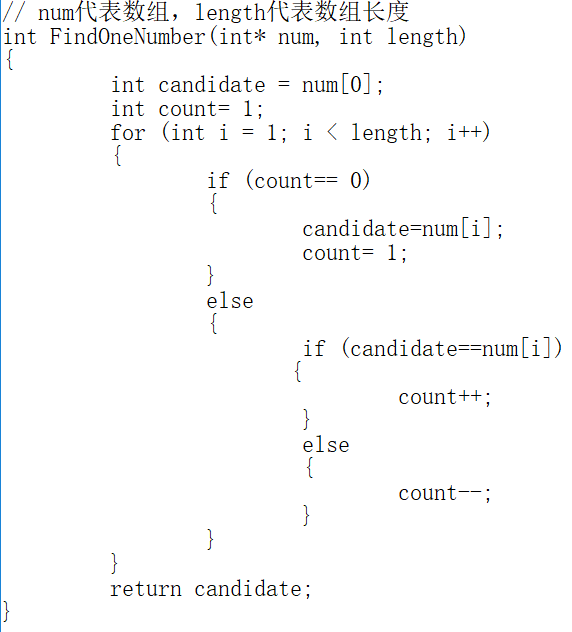
2、找出出现次数超过1/3的两个数
同理:每次删除3个不同的数,最后剩下两个数。
实现步骤:输入数组num
- 定义候选集n1,n2(初始化为不同的数值),对应次数记为c1,c2(初始化为0)
- 若num[i]等于n1或n2,则c1+1或c2+1
- 否则,c1与c2均减1(即删除3个不同的数)
- 若c1=0或c2=0,则更新n1=num[i]或n2=num[i]
- 直到遍历完所有数为止
例如:num={1 2 3 2 2 4 3 3}
- 初始化n1=0,n2=1,c1=c2=0
- 遍历num[0]=1=n2,c2+1=1
- 遍历num[1]=2,因为c1=0,所以n1=2,c1=1
- 遍历num[2]=3,都不同,c1-1=0,c2-1=0
- 遍历num[3]=2=n2,c2+1=1
- 遍历num[4]=2=n2,c2+1=2
- 遍历num[5]=4,因为c1=0,所以n1=4,c1=1
- 遍历num[6]=3,都不同,所以c1-1=0,c2-1=1
- 遍历num[7]=3,因为c1=0,所以n1=3,c1=1
- 遍历完毕,候选集c1=3,c2=2
核心代码:

注:
1)此题中已默认一定存在超过1/2的众数和超过1/3的两个数,若没有说明,还需要对得出来的候选集进行次数验证!
2)其他情形:求超过1/m的数,一样可用此方法解决;即定义m-1个不同的数,以及(m-1)个不同的计数,初始化数为不同值,计数为0,寻找并删除之。
3、若一个数组中,只有一个数出现奇次,其他均出现偶次,找出这个数。
利用异或:相同的数异或为0,不同的数异或为1
- a^a=0,a^b=1
- a^0=0
- a^b=b^a(交换律)
- (a^b)^c=a^(b^c)
总结:奇数个异或是本身,偶数个异或是0,0^a=a,异或满足交换律
例如:1 2 1 2 3 3 3,寻找奇数项
做异或:1^2^1^2^3^3^3=1^1^2^2^3^3^3=0^0^0^3=3




